【DEVOPS】Jenkins使用问题 - 控制台输出乱码
0. 目录
- 1. 问题描述
- 2. 解决方案
- 3. 最终效果
- 4. 总结
1. 问题描述
部门内部对于Jenkins的使用采取的是Master + Slave Work Node的方式,即作为Master节点的Jenkins只负责任务调度,具体的操作由对应的Slave Work Node去执行。
最近团队成员反馈一个问题:一个Linux系统的Slave Work Node的编译日志输出中,中文部分均为乱码(如下图),这造成问题排查效率不高。
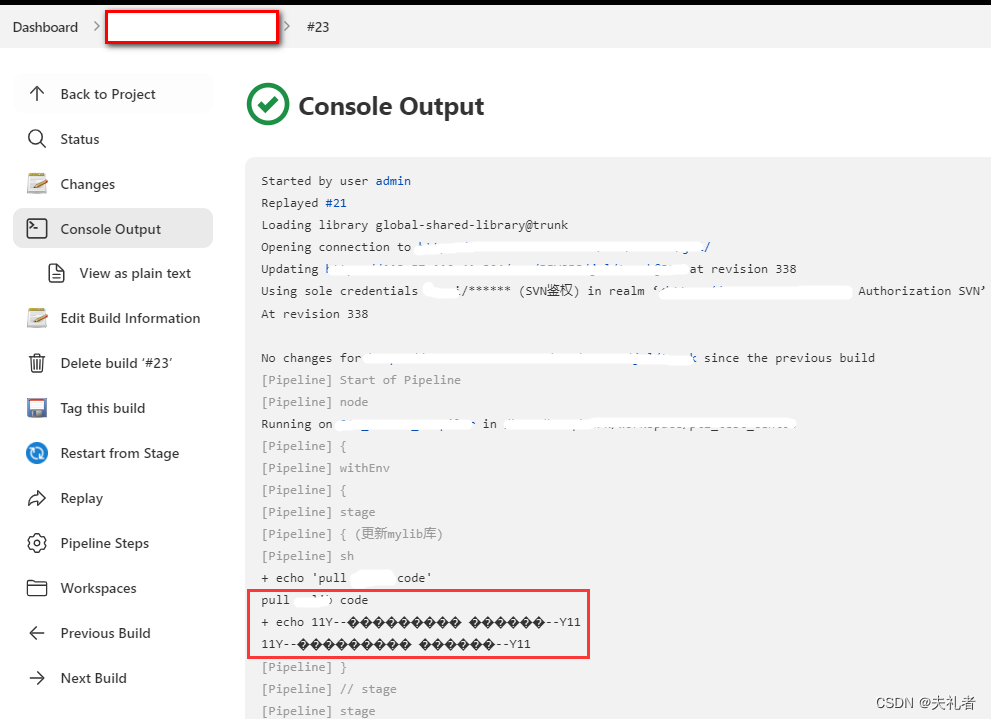
针对以上问题,我们尝试了:
- 在Jenkins的Pipeline脚本中设置
LC_ALL = 'en_US.UTF-8'。 - 确认作为Master节点的Jenkins服务端的启动参数中存在
-Dfile.encoding=UTF-8。 - 确认目标机器Slave Work Node的系统环境变量
echo $LANG/locale。 - 确认作为Master节点的Jenkins服务端的系统环境变量
echo $LANG/locale。 - 在Jenkins的Script Console中设置
System.setProperty('hudson.console.ConsoleCharset', 'UTF-8')。
无一例外,全部失败了。
2. 解决方案
这里先说解决方案。毕竟能够找到这里的,肯定是上面提到的常规方式都尝试失败了。
其实事后回顾,此时此刻就只剩下最后一种可能:作为agent的java程序remoting.jar自身的编码不对劲。
-
确定问题。
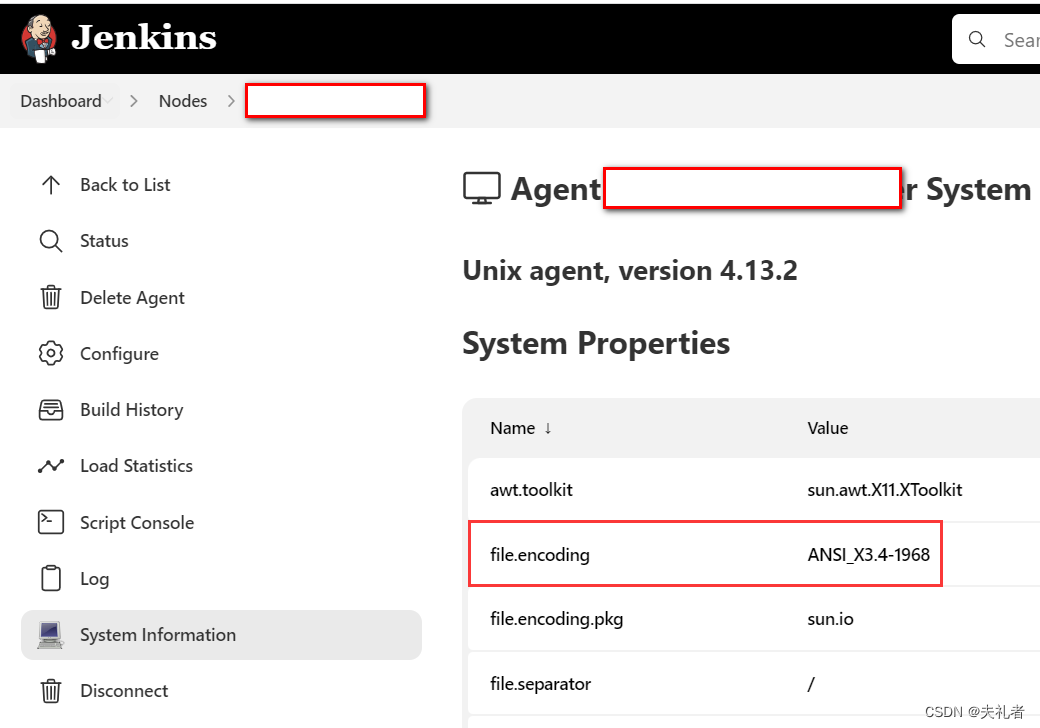
-
调整。
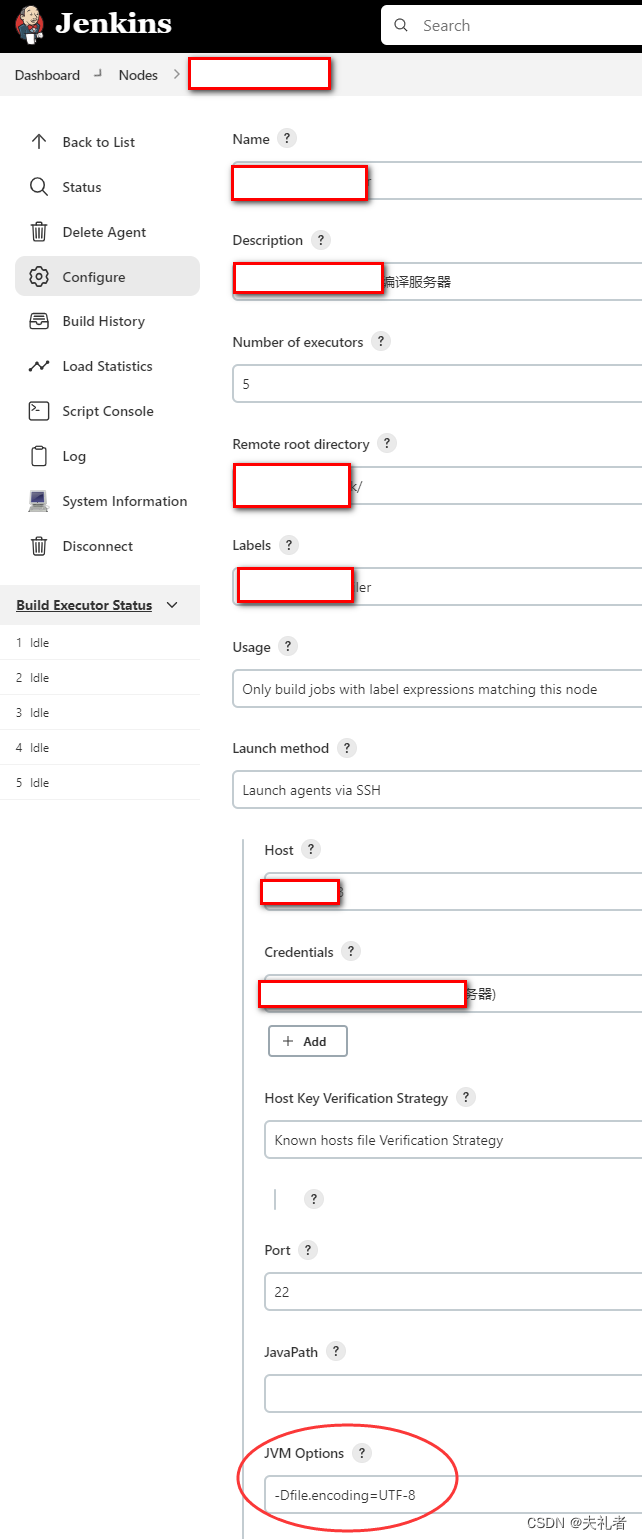
-
验证配置生效。
重启agent之后,应该如下图: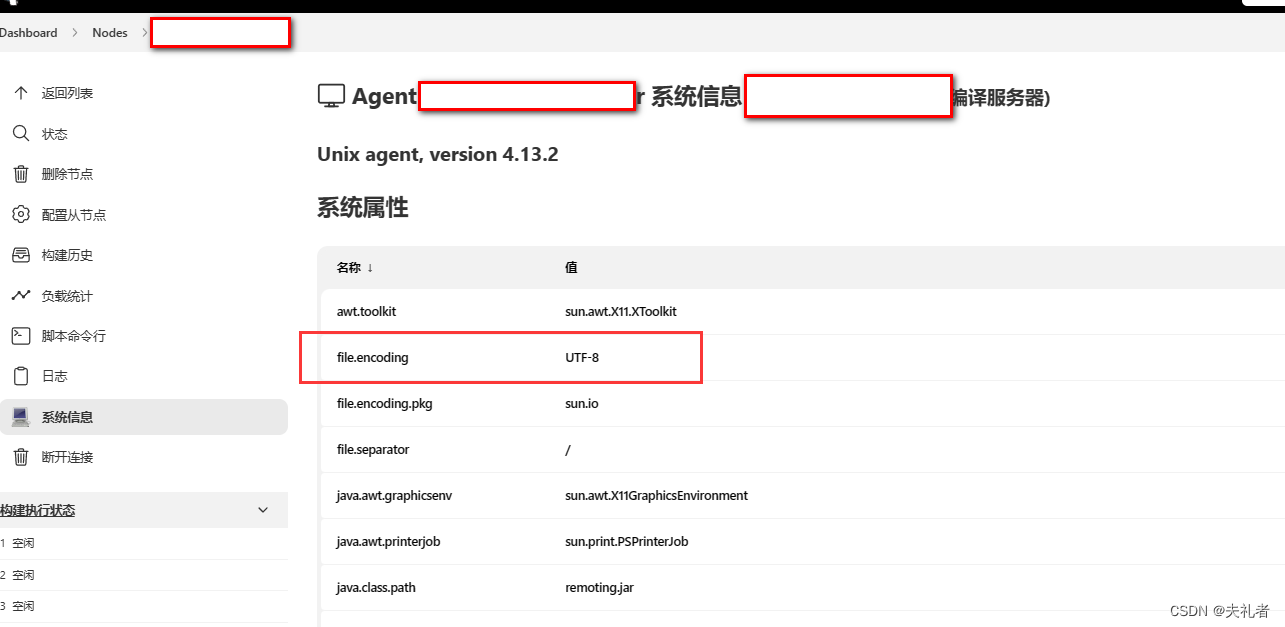
修改前后,Slave Work Node上agent命令参数行对比:

3. 最终效果
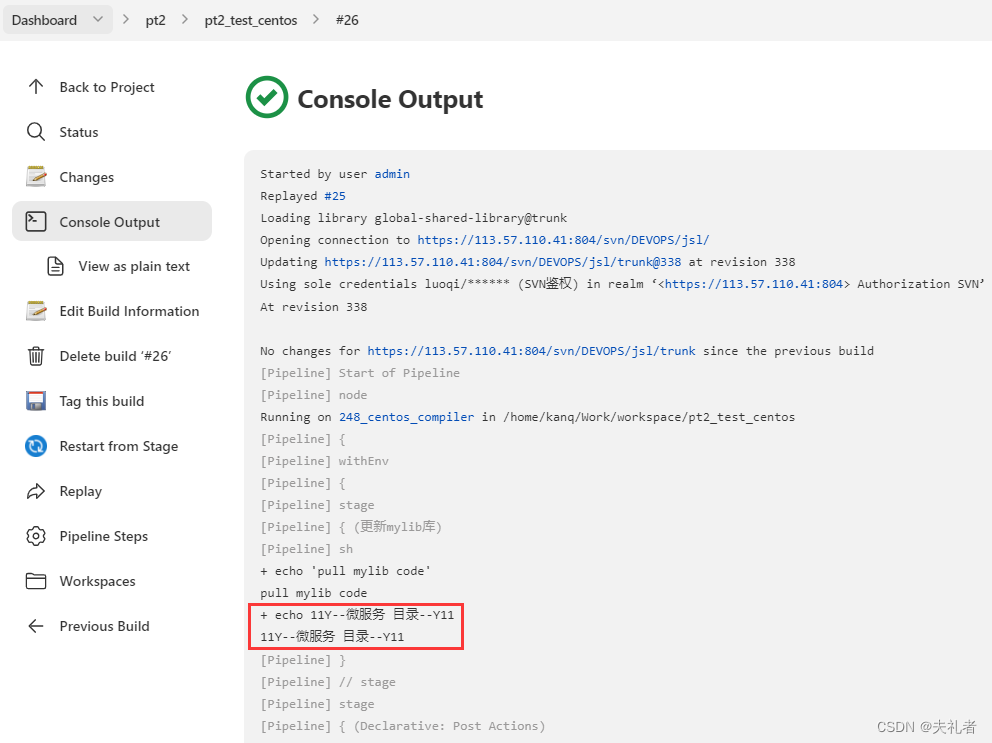
4. 总结
细节是魔鬼。
神在细节之中。
相关文章:

【DEVOPS】Jenkins使用问题 - 控制台输出乱码
0. 目录 1. 问题描述2. 解决方案3. 最终效果4. 总结 1. 问题描述 部门内部对于Jenkins的使用采取的是Master Slave Work Node的方式,即作为Master节点的Jenkins只负责任务调度,具体的操作由对应的Slave Work Node去执行。 最近团队成员反馈一个问题&a…...

logback-spring.xml
<?xml version"1.0" encoding"UTF-8"?> <configuration> <appender name"stdout" class"ch.qos.logback.core.ConsoleAppender"> <encoder> <springProfile name"dev"> <pattern>%d{…...
华为OD机试之报文重排序【Java源码】
题目描述 对报文进行重传和重排序是常用的可靠性机制,重传缓中区内有一定数量的子报文,每个子报文在原始报文中的顺序已知,现在需要恢复出原始报文。 输入描述 输入第一行为N,表示子报文的个数,0 <N ≤ …...

回归预测 | MATLAB实现BES-ELM秃鹰搜索优化算法优化极限学习机多输入单输出回归预测(多指标,多图)
回归预测 | MATLAB实现BES-ELM秃鹰搜索优化算法优化极限学习机多输入单输出回归预测(多指标,多图) 目录 回归预测 | MATLAB实现BES-ELM秃鹰搜索优化算法优化极限学习机多输入单输出回归预测(多指标,多图)效…...

DPU在东数西算背景下如何赋能下一代算力基础设施 中科驭数在未来网络发展大会论道
以ChatGPT为代表的人工智能大模型的快速发展,对网络信息技术创新发展提出了新的挑战,我国东数西算重大工程也在加速布局。以确定性网络、算力网络为代表的未来网络核心技术,正成为决定未来经济和产业发展的关键。 8月23日,第七届…...

2021年12月 C/C++(四级)真题解析#中国电子学会#全国青少年软件编程等级考试
第1题:移动路线 桌子上有一个m行n列的方格矩阵,将每个方格用坐标表示,行坐标从下到上依次递增,列坐标从左至右依次递增,左下角方格的坐标为(1,1),则右上角方格的坐标为(m,n)。 小明是个调皮的孩子,一天他捉来一只蚂蚁,不小心把蚂蚁的右脚弄伤了,于是蚂蚁只能向上或向右…...

ArcGIS Serve Windows下用户密码变更导致Server服务无法启动问题
问题: 因未知原因Windows下的Server安装账户密码变更,但是又忘记了密码,导致,Server服务启动失败,错误1069: 解决方法: 在账户管理界面,重置对应的arcgis账户的密码,…...

React 面试题集锦
目录 如果想要在组件第一次加载后获取该组件的dom元素,应当在以下哪个生命周期中进行 React支持的键盘事件是 使用严格模式(Strict Mode)优点 React 动态引入组件 当使用ReactDOM.unmountComponentAtNode从DOM中卸载组件时 说一下useS…...

xargs命令解决“Argument list too long”
一、xargs命令概述 xargs命令是给其他命令传递参数的一个过滤器,也是组合多个命令的一个工具。它擅长将标准输入数据转换成命令行参数,xargs能够处理管道或者stdin并将其转换成特定命令的命令参数。空格是其默认定界符,管道传递给xargs的输入…...

R语言中<- 的含义
一般语言的赋值是 号,但是 R 语言是数学语言,所以赋值符号与我们数学书上的伪代码很相似,是一个左箭头 <- : 举个例子: a <- 12 b <- 45 print(a b) 以上代码执行结果:57 这个赋值符号是 R …...
知识图谱Neo4j安装到实践全过程
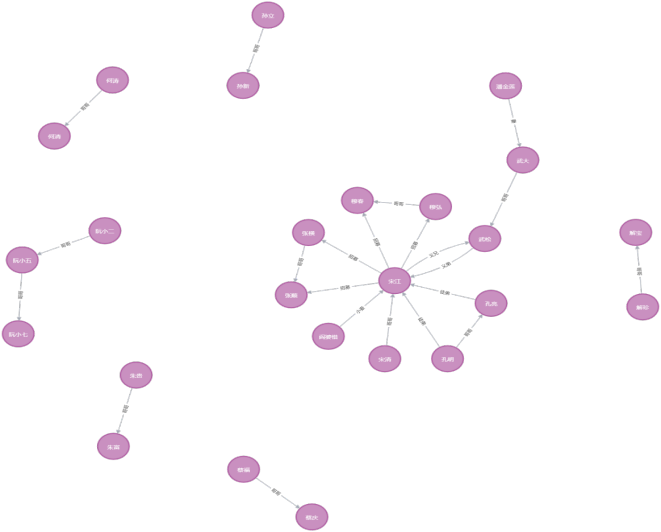
前言: Hello大家好,我是Dream。 在本次实战中,我们将一起完成知识图谱Neo4j安装到实践全过程,探索其中的关系和属性。知识图谱是一种以三元组形式存储的数据结构,由实体、关系和属性组成,能够帮助我们更好地…...
贪心算法:简单而高效的优化策略
在计算机科学中,贪心算法是一种简单而高效的优化策略,用于解决许多组合优化问题。虽然它并不适用于所有问题,但在一些特定情况下,贪心算法能够产生近似最优解,而且计算成本较低。在本文中,我们将深入探讨贪…...

一生一芯6——ubuntu rpm软件安装
ubuntu不支持rpm,需要将rpm软件安装包转成deb进行安装 安装alien sudo apt-get install alien格式转换 sudo alien xxx.rpm 在目录下会生成deb的安装包 软件安装 sudo dpkg -i xxx_amd64.deb 安装完成...

Python练习 函数取列表最小数
练习2:构造一个功能函数,可以解决如下问题: 要求如下: 1,任意输入一个列表,函数可以打印出列表中最小的那个数, 例:输入: 23,56,67,4,17,9 最小数是 :4 方法一: #内置函…...

五种重要的 AI 编程语言
推荐:使用 NSDT场景编辑器 助你快速搭建3D应用场景 简而言之:决定从哪种语言开始可能会令人生畏。 不用担心!本文将解释 AI 中使用的最流行编程语言背后的基础知识,并帮助您决定首先学习哪种语言。对于每种语言,我们将…...
【linux】2 make/Makefile和gitee
文章目录 一、Linux项目自动化构建工具-make/Makefile1.1 背景1.2 实例代码1.3 原理1.4 项目清理 二、linux下第一个小程序-进度条2.1 行缓冲区2.2 进度条 三、git以及gitee总结 ヾ(๑╹◡╹)ノ" 人总要为过去的懒惰而付出代价ヾ(๑╹◡╹)ノ" 一…...
)
db-gpt安装指南(docker版本)
1 下载源码 下载v0.3.5的源码,截止今天(20230823)建议安装这个“稳定”版本。 2 构建镜像 依照自己硬件环境,看看是否要调整一下启动参数。 bash docker/build_all_images.sh \ --base-image nvidia/cuda:11.7.1-devel-ubuntu…...

「Java」《深度解析Java Stream流的优雅数据处理》
《深度解析Java Stream流的优雅数据处理》 一、引言1.1 背景1.2 Stream流的意义 二、Stream流的基本概念2.1 什么是Stream流2.2 Stream与传统集合的对比 三、创建Stream流3.1 通过集合创建Stream3.2 使用Arrays和Stream.of创建Stream3.3 从文件和网络流创建Stream 四、 中间操作…...
【云驻共创】华为云之手把手教你搭建IoT物联网应用充电桩实时监控大屏
文章目录 前言1.什么是充电桩2.什么是IOT3.什么是端、边、云、应用协同4.什么是Astro轻应用 一、玩转lOT动态实时大屏(线下实际操作)1.Astro轻应用说明1.1 场景说明1.2 资费说明1.3 整体流程 2.操作步骤2.1 开通设备接入服务2.2 创建产品2.3 注册设备2.4…...

Hadoop分布式计算与资源调度:打开专业江湖的魔幻之门
文章目录 版权声明一 分布式计算概述1.1 分布式计算1.2 分布式(数据)计算模式1.3 小结 二 MapReduce概述2.1 分布式计算框架 - MapReduce2.2 MapReduce执行原理2.3 小结 三 YARN概述3.1 YARN & MapReduce3.2 资源调度3.3 程序的资源调度3.4 YARN的资…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...
