算法通关村第5关【青铜】| Hash和队列的特征
1.Hash基础
(1)基础
哈希也称为散列,通过算法变成固定长度的输出值,存入对应的位置
例如这个算法为取模算法,index=number 模 7
存入1到15
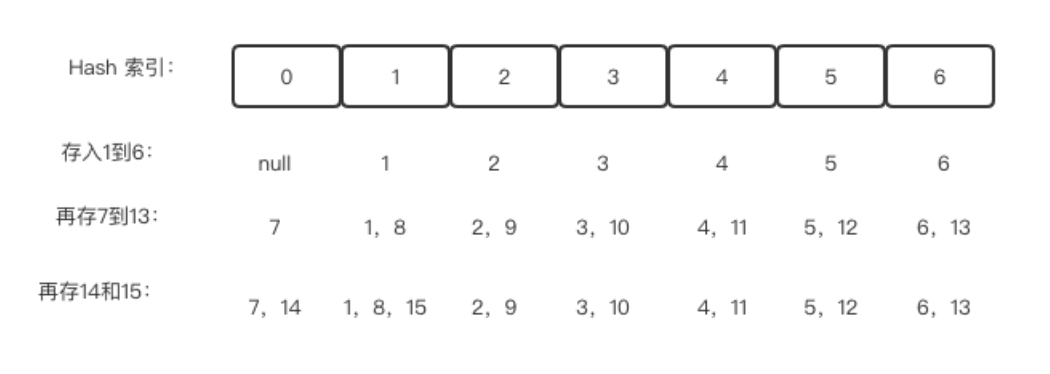
(2)碰撞处理
当多个元素映射到同一位置上时就产生了碰撞
哈希碰撞处理是在使用哈希函数时,不同的键可能映射到相同的哈希值(哈希冲突)时的解决方法。哈希碰撞处理是为了确保不同的键可以在哈希表中正确存储和检索,从而维护哈希表的性能和正确性。
以下是几种常见的哈希碰撞处理方法:
链地址法(Chaining): 这是一种常见的方法,通过在哈希桶位置上维护一个链表(或其他数据结构),将发生冲突的键值对添加到链表中。在查找或删除操作时,遍历链表来找到对应的键值对。
开放定址法(Open Addressing): 在这种方法中,当发生冲突时,会顺序地在哈希表中的其他位置寻找空闲的位置来存储键值对。这包括线性探测、二次探测、双重哈希等策略。
再哈希法(Rehashing): 当发生冲突时,计算另一个哈希函数,然后将键值对存储在新的哈希桶位置上。这可以有效地减少冲突。
建立一个“桶”的链表: 这是一种类似于链地址法的方法,但不是在每个哈希桶位置上维护一个链表,而是在发生冲突的哈希桶位置上维护一个链表。
完全二叉树: 将键值对按照哈希值顺序存储在完全二叉树的节点上。这种方法在特定情况下可以提供较好的性能。
开放定址法
开放定址法的主要思想是,当发生哈希冲突时,不仅仅将数据存储在哈希桶中,而是根据某种算法找到一个不冲突的位置,将数据存储在那里。这就需要一个探测序列(probing sequence),它是一系列指示位置的步骤,用于寻找下一个可用的位置。
常见的开放定址法包括:
-
线性探测(Linear Probing): 在发生冲突时,按顺序检查下一个位置,直到找到一个空闲位置为止。
-
二次探测(Quadratic Probing): 在发生冲突时,按照某个步长的平方逐渐增加位置,直到找到一个空闲位置为止。
-
双重散列(Double Hashing): 在发生冲突时,使用第二个哈希函数计算一个步长,然后在哈希表中逐渐增加位置,直到找到一个空闲位置为止。
开放定址法的优点是它对于内存的利用更有效,因为数据存储在数组中,没有额外的指针。然而,它在负载因子高时可能会导致聚集现象(clustering),即一些位置上会有很多连续的元素,而其他位置则很少使用。这可能会降低性能。
链地址法
"链地址法"(Chaining)是一种哈希表解决哈希冲突的方法之一。在哈希表中,不同的键可能会映射到相同的哈希桶位置,这就产生了哈希冲突。链地址法通过在每个哈希桶位置上维护一个链表(或其他数据结构)来处理这种冲突。
具体来说,当发生哈希冲突时,链地址法将冲突的键值对添加到哈希桶位置对应的链表中。每个链表节点包含一个键值对。当需要插入、查找或删除一个键值对时,先计算哈希值找到对应的哈希桶位置,然后在该位置的链表中进行操作。
以下是链地址法的基本步骤:
-
插入: 计算键的哈希值,找到对应的哈希桶位置。如果该位置为空,则在该位置插入键值对。如果该位置已经有其他键值对存在(即发生冲突),则在链表中继续插入新的键值对。
-
查找: 计算键的哈希值,找到对应的哈希桶位置。然后遍历链表,查找包含该键的节点。
-
删除: 计算键的哈希值,找到对应的哈希桶位置。然后遍历链表,找到包含该键的节点,并进行删除操作。
链地址法的优点是它相对简单,可以有效地解决哈希冲突。然而,当哈希冲突较多时,链表可能会变得较长,导致操作的时间复杂度增加。为了保持哈希表的高效性能,需要根据数据分布情况来选择合适的哈希函数,并根据情况动态调整哈希桶的数量。另外,当链表过长时,可以考虑使用更高效的数据结构,如红黑树,来替代链表,以提高查找效率。
2.队列基础
FIFO先进先出的线性表
基于链表实现
尾插+头删
public class MyLinkQueue {static class Node {public int data;public Node next;public Node(int data) {this.data = data;}}private Node front;private Node rear;private int size;//无参构造初始化public MyLinkQueue() {this.front = null;this.rear = null;}public boolean isEmpty() {return front == null;}//尾插public void push(int data){Node node = new Node(data);if (isEmpty()){front = node;rear = node;}else{rear.next = node;rear = node;}size++;}//头删public int pop(){if (isEmpty()){throw new EmptyStackException();}int res = front.data;front = front.next;size--;return res;}public int size(){return size;}public void traverse(){Node t = front;while(t!=null){System.out.println(t.data);t = t.next;}}public static void main(String[] args) {MyLinkQueue queue = new MyLinkQueue();queue.push(10);queue.push(20);queue.push(30);System.out.println("Queue elements:");queue.traverse(); // Output: 10 20 30System.out.println("Dequeued element: " + queue.pop()); // Output: 10System.out.println("Queue size: " + queue.size()); // Output: 2queue.push(40);queue.push(50);System.out.println("Queue elements:");queue.traverse(); // Output: 20 30 40 50System.out.println("Queue size: " + queue.size()); // Output: 4}}
相关文章:

算法通关村第5关【青铜】| Hash和队列的特征
1.Hash基础 (1)基础 哈希也称为散列,通过算法变成固定长度的输出值,存入对应的位置 例如这个算法为取模算法,indexnumber 模 7 存入1到15 (2)碰撞处理 当多个元素映射到同一位置上时就产生…...

C++:函数
函数参数的传递机制 C的每个程序至少有一个函数,即主函数main(),函数也是类的方法的实现手段。C的函数包括两类:预定于函数和用户自定义函数。 函数的定义格式为: <返回值类型><函数名>(<参数列表>) <函…...
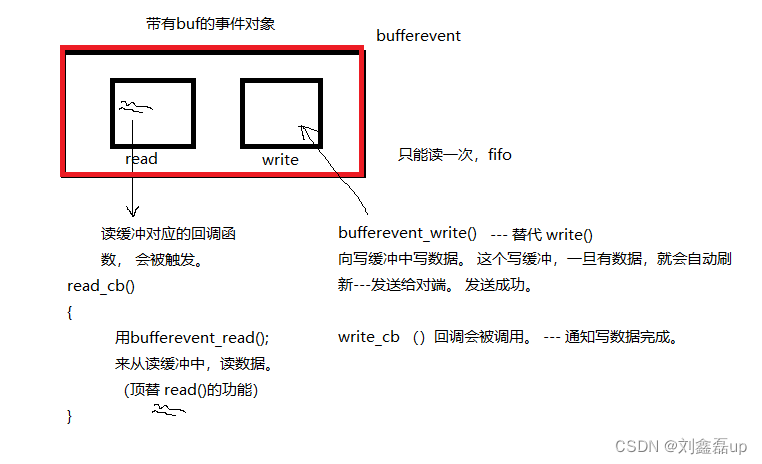
Linux网络编程:libevent事件通知库
文章目录: 一:libevent库 二:libevent框架 1.常规事件event 1.1 创建事件event(event_new) 1.2 添加事件到 event_base(event_add) 1.3 从event_base上摘下事件(event_del&a…...

java.lang.reflect.InvocationTargetException:null报未知异常
在项目上线过程中,突然出现大量异常信息,堆栈信息如下: java.lang.reflect.InvocationTargetException: null at jdk .internal.reflect.GeneratedMethodAccessor792 .invoke(Unknown Source) ~[?:?] at jdk.internal.reflect.DelegatingM…...

MySQL高级篇——MySQL架构篇1(Linux下MySQL8的安装与使用)
目录 0 安装前0.1 Linux系统及工具的准备0.2 查看是否安装过MySQL0.3 MySQL的卸载 1 MySQL8的Linux版安装1.1 MySQL的4大版本1.2 下载MySQL指定版本1.3 CentOS7下检查MySQL依赖1.4 CentOS7下MySQL安装过程 2 MySQL登录2.1 首次登录2.2 修改密码2.3 设置远程登录 3 MySQL 8 的密…...
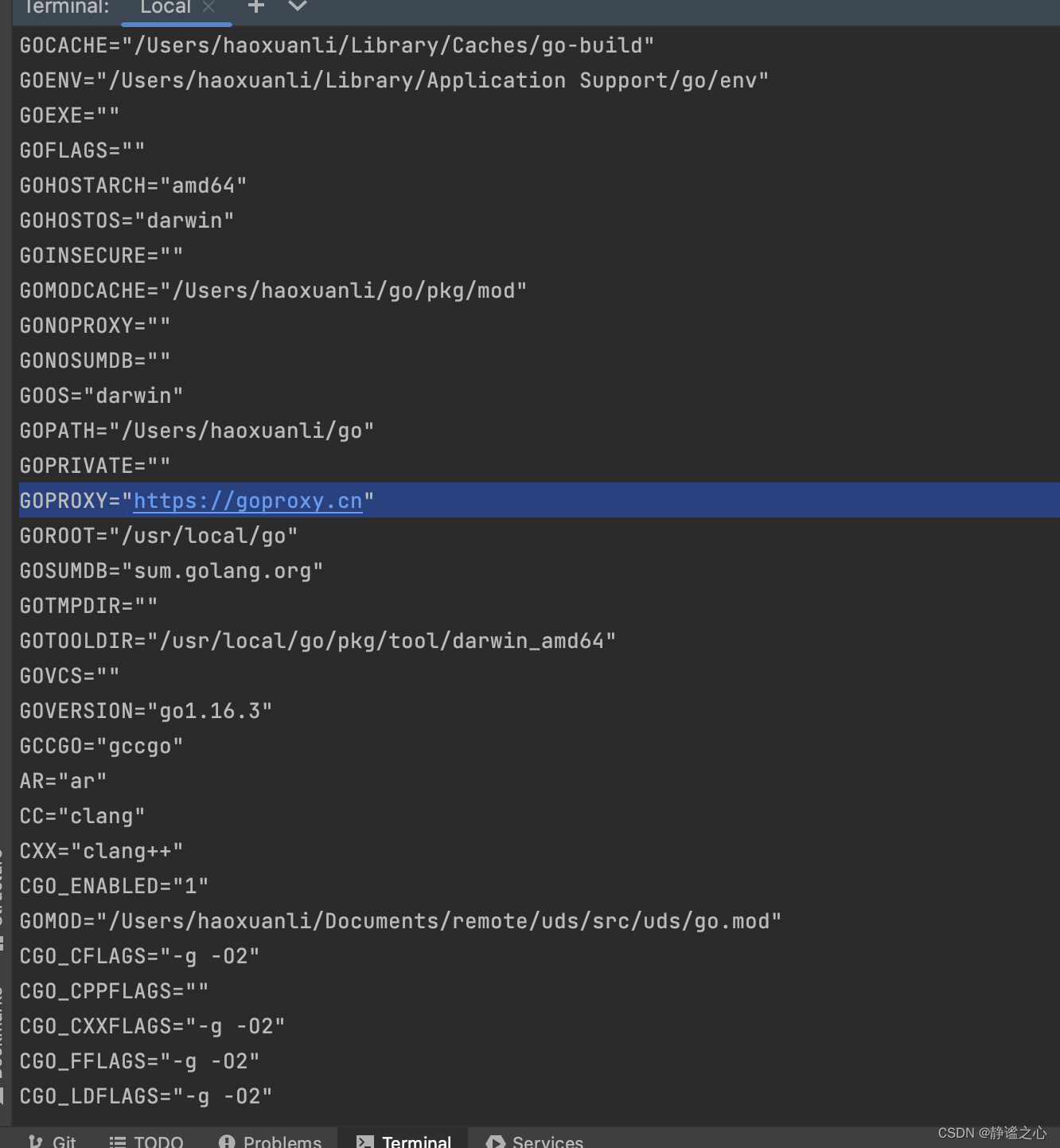
解决 go mod tidy 加载模块超时
如果go mod tidy 加载模块超时 解决方法 修改GOPROXY: 查看go环境相关信息: go envgo env -w GOPROXYhttps://goproxy.cn...

金融市场中的机器学习;快手推出自研语言模型“快意”
🦉 AI新闻 🚀 OpenAI可能面临《纽约时报》的起诉,侵犯知识产权引发争议 摘要:OpenAI使用《纽约时报》的文章和图片来训练AI模型,违反了《纽约时报》的服务条款,可能面临巨大损失。此前,也有其…...

【面试刷题】——什么是深拷贝和浅拷贝?
深拷贝(Deep Copy)和浅拷贝(Shallow Copy)是在编程中用来描述对象拷贝的两个概念,特别是在涉及对象包含其他对象(如嵌套数据结构、指针等)的情况下。 浅拷贝(Shallow Copyÿ…...

物联网(IoT)安全挑战与解决方案: 分析物联网设备面临的安全威胁,以及如何设计和管理安全的IoT生态系统
第一章:引言 随着科技的飞速发展,物联网(IoT)作为连接世界的桥梁,已经成为现代社会不可或缺的一部分。然而,随着IoT设备数量的不断增加,其安全问题也日益显著。本文将深入探讨IoT领域面临的安全…...
Ubuntu 22.04.3 LTS 维护更新发布
近日消息,Canonical 今天发布了代号为 Jammy Jellyfish、长期支持的 Ubuntu 22.04 第 3 个维护版本更新,距离上个版本相隔 6 周时间。 Ubuntu 22.04.3 LTS 最大的亮点在于内核升级到 Linux Kernel 6.2,此外 Mesa 图形堆栈也升级到 23.0.4 版…...
平安健康,找到了医疗服务的价值密码
健康是人类的永恒需求,围绕医疗和健康服务衍生的产业,却苦于无法和用户建立足够紧密、长期的联系。由此,也不得不面临价值从何而来的问题。 作为医疗服务领域的代表性企业,平安健康医疗科技有限公司(股票简称“平安好…...

❤ vue 使用原生组件
❤ vue 使用原生组件 1、做一个input输入框验证开始 ① 想让我们的input输入框类型为时间,只需要为我们的输入框简单的加一个类型的type即可 <input type"date" id"birthday" name"birthday" placeholder"年/月/日"&…...

4.12 TCP 连接,一端断电和进程崩溃有什么区别?
目录 TCP keepalive TCP 的保活机制 主机崩溃 进程崩溃 有数据传输的场景 客户端主机宕机,又迅速重启 客户端主机宕机,一直没有重启 TCP连接服务器宕机和进程退出情况总结 TCP keepalive TCP 的保活机制 TCP 保活机制需要通过 socket 接口设置 S…...

十二、pikachu之URL重定向
文章目录 1、URL重定向概述2、实战3、URL跳转的几种方式:3.1 META标签内跳转3.2 javascript跳转3.3 header头跳转 1、URL重定向概述 不安全的url跳转问题可能发生在一切执行了url地址跳转的地方。如果后端采用了前端传进来的(可能是用户传参,或者之前预埋…...

贝叶斯公式中的动词 命名技巧
一项血液化验有95%的把我诊断某种疾病,但是,这项化验用于健康人也会有1%的“伪阳性”结果(即如果一个健康人接受这项化验,则化验结果乌镇此人患有该疾病的概率是0.01)。如果该疾病的患者事实上只占总人口的0.5%,若某人化验结果为阳…...
ctfshow-web13 文件上传
0x00 前言 CTF 加解密合集CTF Web合集 0x01 题目 0x02 Write Up 首先看到是一个上传页面,测试其他无果,遂进行目录遍历,发现upload.php.bak文件 可以看到这里的限制条件,大小,以及内容,这里可以使用.use…...

Python项目开发案例————学生信息管理系统(附源码)
一、学生信息管理系统 本文使用Python语言开发了一个学生信息管理系统,该系统可以帮助教师快速录入学生的信息,并且对学生的信息进行基本的增、删、改、查操作;还可以实时地将学生的信息保存到磁盘文件中。 1.1 需求分析 为了顺应互联网时代…...

2023-08-25力扣每日一题
链接: 1448. 统计二叉树中好节点的数目 题意: 判断根节点到每个节点X的过程中,如果没有值大于X,则该节点为好节点,求好节点数量 解: 由于求根节点到其他节点的路径,则使用dfs算法ÿ…...

Vue3中的计算属性和属性监听
compute计算属性 Vue3中可以通过 compute进行监听计算属性,他返回的是一个ref的对象,也就是说 通过compuye这种方式计算属性实际上是进行了ref的操作 import { computed } from vue const user reactive({firstName: A,lastName: B }) // 只有getter的…...
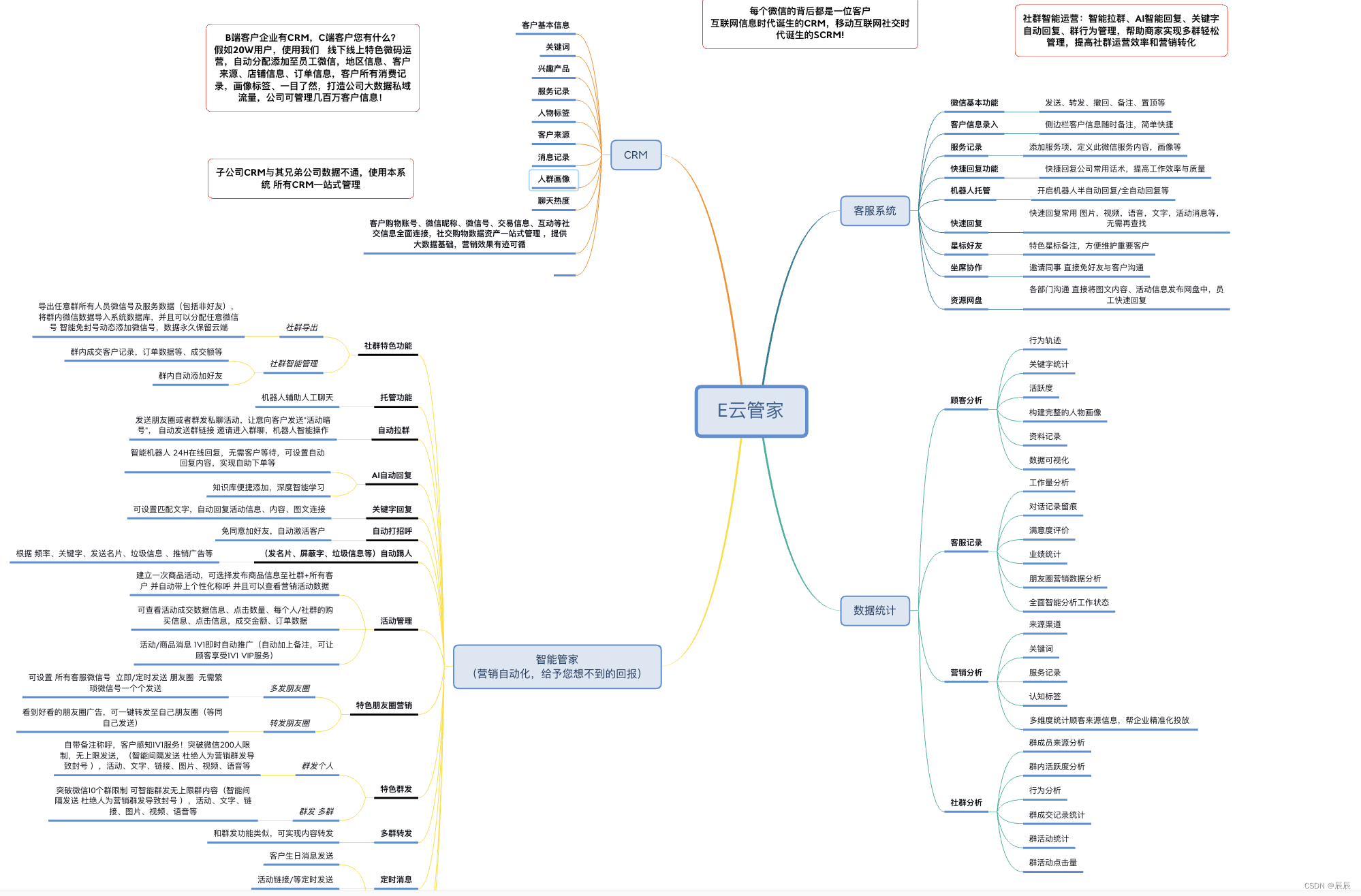
微信开发之一键修改群公告的技术实现
简要描述: 设置群公告 请求URL: http://域名地址/setChatRoomAnnouncement 请求方式: POST 请求头Headers: Content-Type:application/jsonAuthorization:login接口返回 参数: 参数名必…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...
