nginx 反向代理的原理
Nginx(发音为"engine X")是一个高性能、轻量级的开源Web服务器和反向代理服务器。它的反向代理功能允许将客户端的请求转发到后端服务器,然后将后端服务器的响应返回给客户端。下面是Nginx反向代理的工作原理:
1.客户端发送请求: 当客户端(如Web浏览器)发起一个HTTP请求时,请求会发送到Nginx服务器。
2.Nginx接收请求: Nginx服务器接收到客户端的请求。
3.查找匹配的位置: Nginx会根据配置文件中的规则(在server块内的location指令)来确定如何处理这个请求。每个location块可以定义不同的处理规则,比如静态文件服务、反向代理等。
4.反向代理配置: 如果请求需要被反向代理,Nginx会将请求转发给预定义的后端服务器。这些后端服务器可以是同一台机器上的不同端口,也可以是不同的机器。Nginx会使用反向代理配置中指定的负载均衡算法来选择一个后端服务器来处理请求。
5.建立连接: Nginx与选择的后端服务器建立连接,并将客户端的请求转发给后端服务器。
6.后端服务器处理请求: 后端服务器接收到Nginx发送的请求,并根据请求的内容进行处理,可以是处理动态内容、查询数据库等。
7.后端服务器响应: 后端服务器生成响应,包括HTTP状态码、响应头部和响应主体。然后将响应发送回Nginx服务器。
8.Nginx接收响应: Nginx服务器接收到后端服务器的响应。
9.响应客户端: Nginx将后端服务器的响应发送回客户端,作为最终的响应。
10.客户端显示响应: 客户端(浏览器)收到响应后,会根据响应的内容进行显示,可能是网页、图片、文本等。
通过这种方式,Nginx实现了反向代理功能,使得客户端无需直接访问后端服务器,而是通过Nginx作为中间层来进行请求和响应的转发,从而提高了系统的可伸缩性、安全性和性能。此外,Nginx还可以通过配置多个后端服务器和负载均衡算法来实现高可用性和分布式处理。
相关文章:

nginx 反向代理的原理
Nginx(发音为"engine X")是一个高性能、轻量级的开源Web服务器和反向代理服务器。它的反向代理功能允许将客户端的请求转发到后端服务器,然后将后端服务器的响应返回给客户端。下面是Nginx反向代理的工作原理: 1.客户端…...

【SpringBoot】第二篇:RocketMq使用
背景: 本文会介绍多种案例,教大家如何使用rocketmq。 一般rocketmq使用在微服务项目中,属于分模块使用。这里使用springboot单体项目来模拟使用。 本文以windows系统来做案例。 下载rocketmq和启动: RocketMQ 在 windows 上运行…...

飞天使-vim简单使用技巧
此文是记录技巧使用,如果想节约时间,可以直接看最后一个章节 vim 的介绍 vim号称编辑器之神,唯快不破,可扩展,各种插件满天飞。 vi 1991 vim 1.14 vim四种模式 普通模式: 移动光标, 删除文本,…...

分布式搜索引擎----elasticsearch
目录 1、初识elasticsearch 1.1、什么是elasticsearch 1.2.ELK技术栈 2、正向索引和倒排索引 2.1、正向索引 2.2、倒排索引 2.3、正向索引和倒排索引的区别 3、elasticsearch中的概念理解 3.1、文档和字段 3.2、索引和映射 3.3、mysql与elasticsearch 1、初识elasti…...

AnnotationConfigApplicationContext类和ClasspathXmlApplicationContext类的区别?
在 Spring Framework 中,AnnotationConfigApplicationContext 和 ClasspathXmlApplicationContext 是两个不同的应用程序上下文实现,用于配置和管理 Spring Bean 容器。它们之间的主要区别在于配置的方式和使用场景。 1. **AnnotationConfigApplication…...
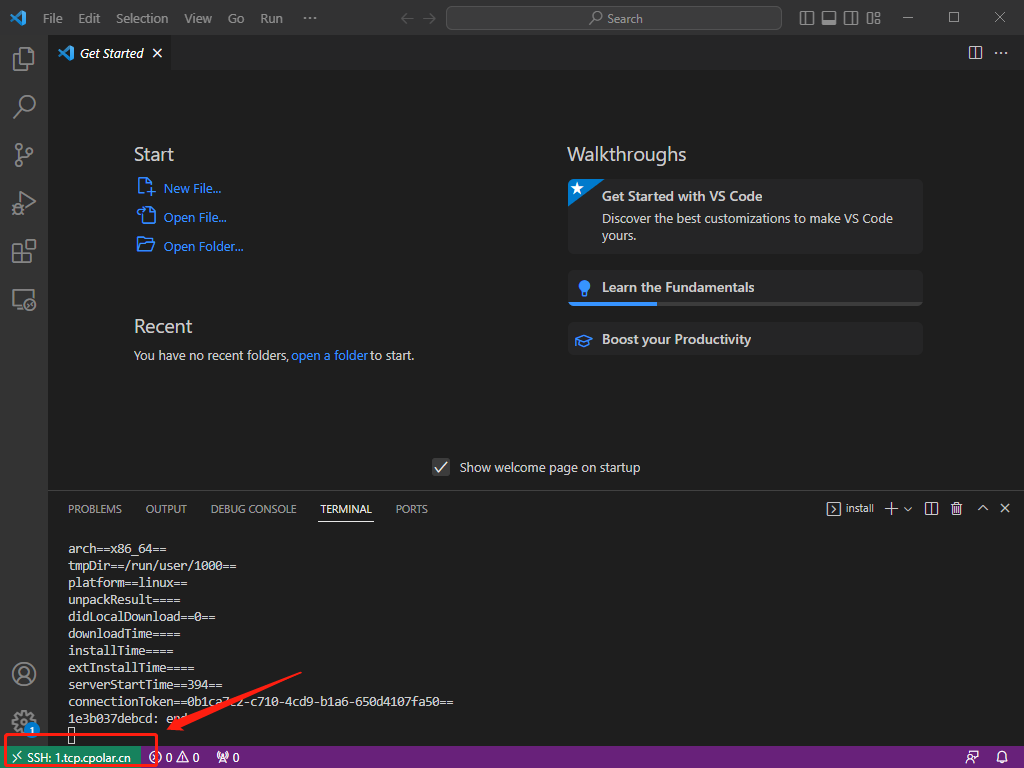
使用VSCode SSH实现公网远程连接本地服务器开发的详细教程
文章目录 前言1、安装OpenSSH2、vscode配置ssh3. 局域网测试连接远程服务器4. 公网远程连接4.1 ubuntu安装cpolar内网穿透4.2 创建隧道映射4.3 测试公网远程连接 5. 配置固定TCP端口地址5.1 保留一个固定TCP端口地址5.2 配置固定TCP端口地址5.3 测试固定公网地址远程 前言 远程…...
Codeforces Round 894 (Div. 3)
还是打一下卡!!! (A,B,C) 目录 A. Gift Carpet 链接 : 题面 : 题目意思 : 思路 : 代码 : B. Sequence Game 链接 : 题面 : 编辑 题目意思 : 思路 : 代码 : C. Flower City Fence 原题链接 : 题面 : 题目意思 : 思路 : 代码 : A. Gift Carpet 链…...
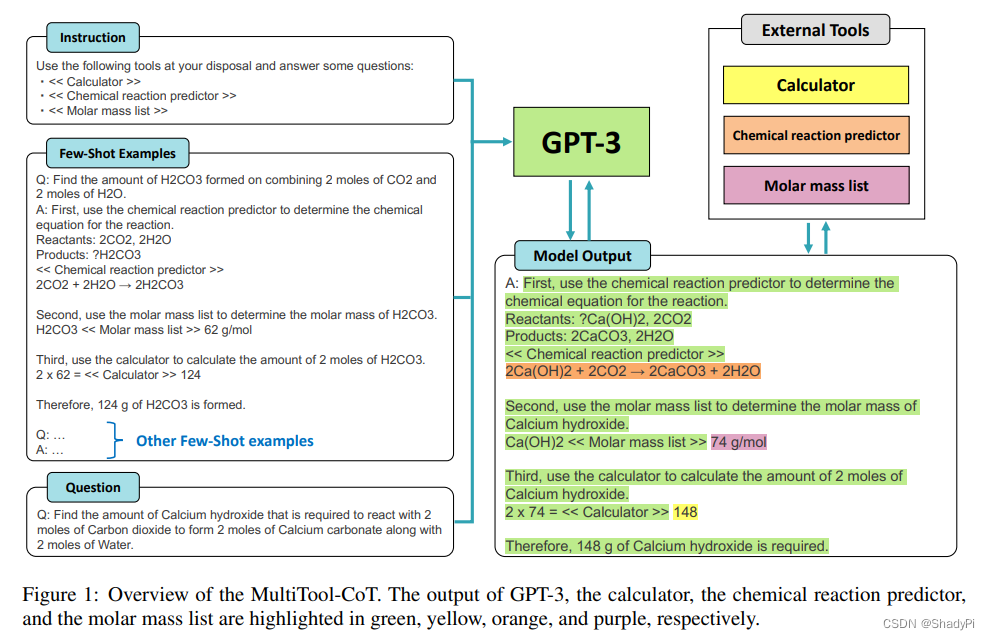
ACL2023 Prompt 相关文章速通 Part 1
Accepted Papers link: ACL2023 main conference accepted papers 文章目录 Accepted PapersPrompter: Zero-shot Adaptive Prefixes for Dialogue State Tracking Domain AdaptationQuery Refinement Prompts for Closed-Book Long-Form QAPrompting Language Models for Lin…...
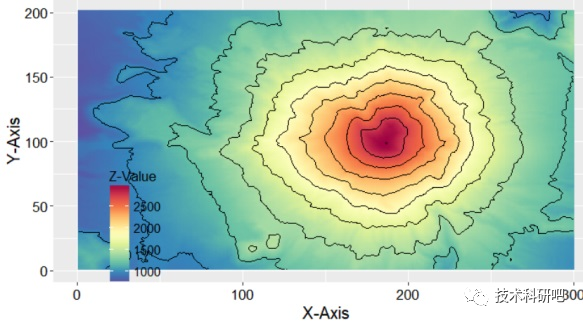
“R语言+遥感“水环境综合评价方法
详情点击链接:"R语言遥感"水环境综合评价方法 一:R语言 1.1 R语言特点(R语言) 1.2 安装R(R语言) 1.3 安装RStudio(R语言) (1)下载地址 &…...
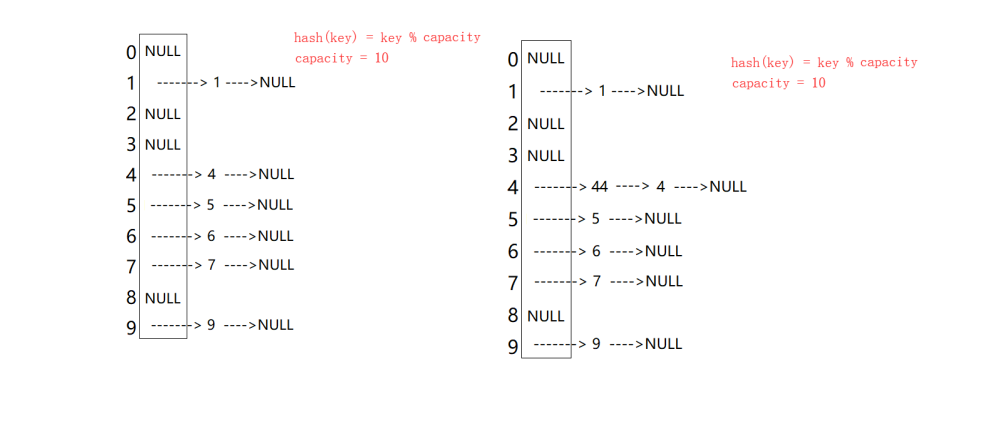
数据结构之哈希
哈希 1. 哈希概念2. 哈希冲突3. 哈希冲突解决3.1 哈希表的闭散列3.2 哈希表的开散列 2. 哈希的应用2.1 位图2.2 布隆过滤器 哈希(Hash)是一种将任意长度的二进制明文映射为较短的二进制串的算法。它是一种重要的存储方式,也是一种常见的检索方…...
-散点图(一))
可视化绘图技巧100篇基础篇(七)-散点图(一)
目录 前言 适用场景 图例 普通散点图与可视化 曲线图 气泡图...

关于什么是框架
框架(Framework)是一个框子——指其约束性,也是一个架子——指其支撑性。 IT语境中的框架,特指为解决一个开放性问题而设计的具有一定 性的支撑结构。在此结构上约束可以根据具体问题扩展、安插更多的组成部分,从而更迅…...

iOS开发Swift-集合类型
集合基本类型:数组 Array (有序), 集合 Set (无序不重复), 字典 Dictionary (无序键值对) 1.数组 Arrays (1)数组的表示 Array<Element> [Element](2)创建空数组 var someInts: [Int] [] someInts.count //数组长度(3)带值数组 var…...
【keepalived双机热备与 lvs(DR)】
目录 一、概述 1.简介 2.原理 3.作用 二、安装 1.配置文件 2.配置项 三、功能模块 1.core 2.vrrp 3.check 四、配置双机热备 1.master 2.backup 五、验证 1.ping验证 2.服务验证 六、双机热备的脑裂现象 七、keepalivedlvs(DR) 1.作…...

C++笔记之静态成员函数可以在类外部访问私有构造函数吗?
C笔记之静态成员函数可以在类外部访问私有构造函数吗? code review! 静态成员函数可以在类外部访问私有构造函数。在C中,访问控制是在编译时执行的,而不是在运行时执行的。这意味着静态成员函数在编译时是与类本身相关联的,而不…...

最新SQLMap进阶技术
SQLMap进阶:参数讲解 (1)–level 5:探测等级。 参数“–level 5”指需要执行的测试等级,一共有5个等级(1~5级),可不加“level”,默认是1级。可以在xml/payloads.xml中看…...
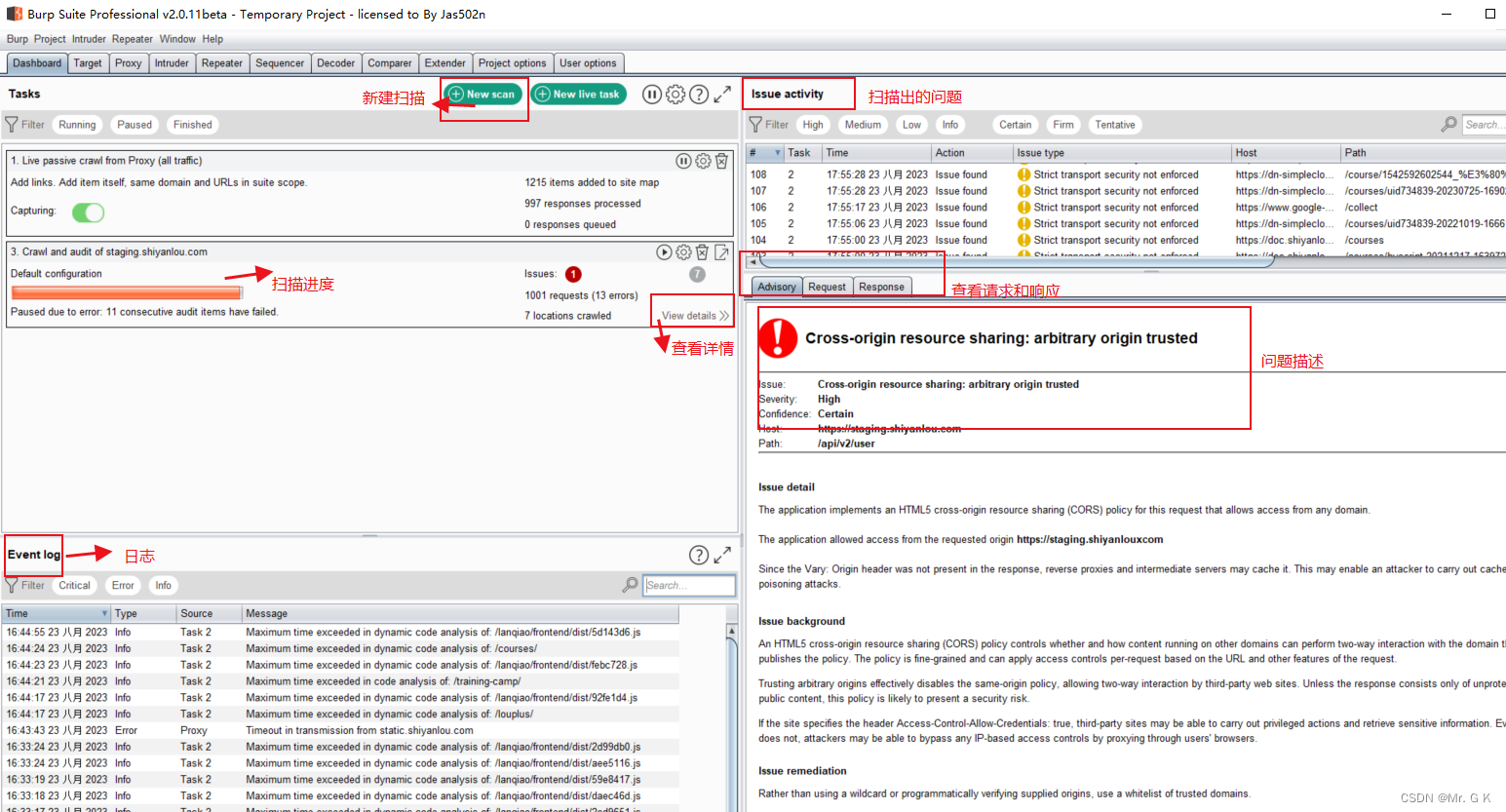
【BurpSuite常用功能介绍】
BurpSuite的使用 1.运行BurpSuite 2.代理设置 打开软件后,我们第一件事就应该去调试软件和浏览器的代理,让BURP能够正常工作抓包 proxy--options,我端口默认使用8080 然后我们打开一个浏览器,进入代理设置 (注意一点࿰…...

Leetcode 108. 将有序数组转换为二叉搜索树
108. 将有序数组转换为二叉搜索树 分析 给定一个有序数组,要求转换为二叉搜索树。 数组是有序的,并且要求二叉树。 这里看到数组是有序的,马上想到二分,但是又不需要完全二分 实现。 再复习二叉搜索树的结构特点: 左…...

小匠物联联合亚马逊云助力企业数智化出海
如何让家电企业出海产品数智化之路走上康庄大道?8月25日,亚马逊云科技[创新成长企业专列]这趟上云快车将开往宁波站,助力宁波的制造、软件等企业扬帆起航!现场举办“亚马逊云科技助力企业出海数智沙龙”,小匠物联受邀出席。 会议现…...
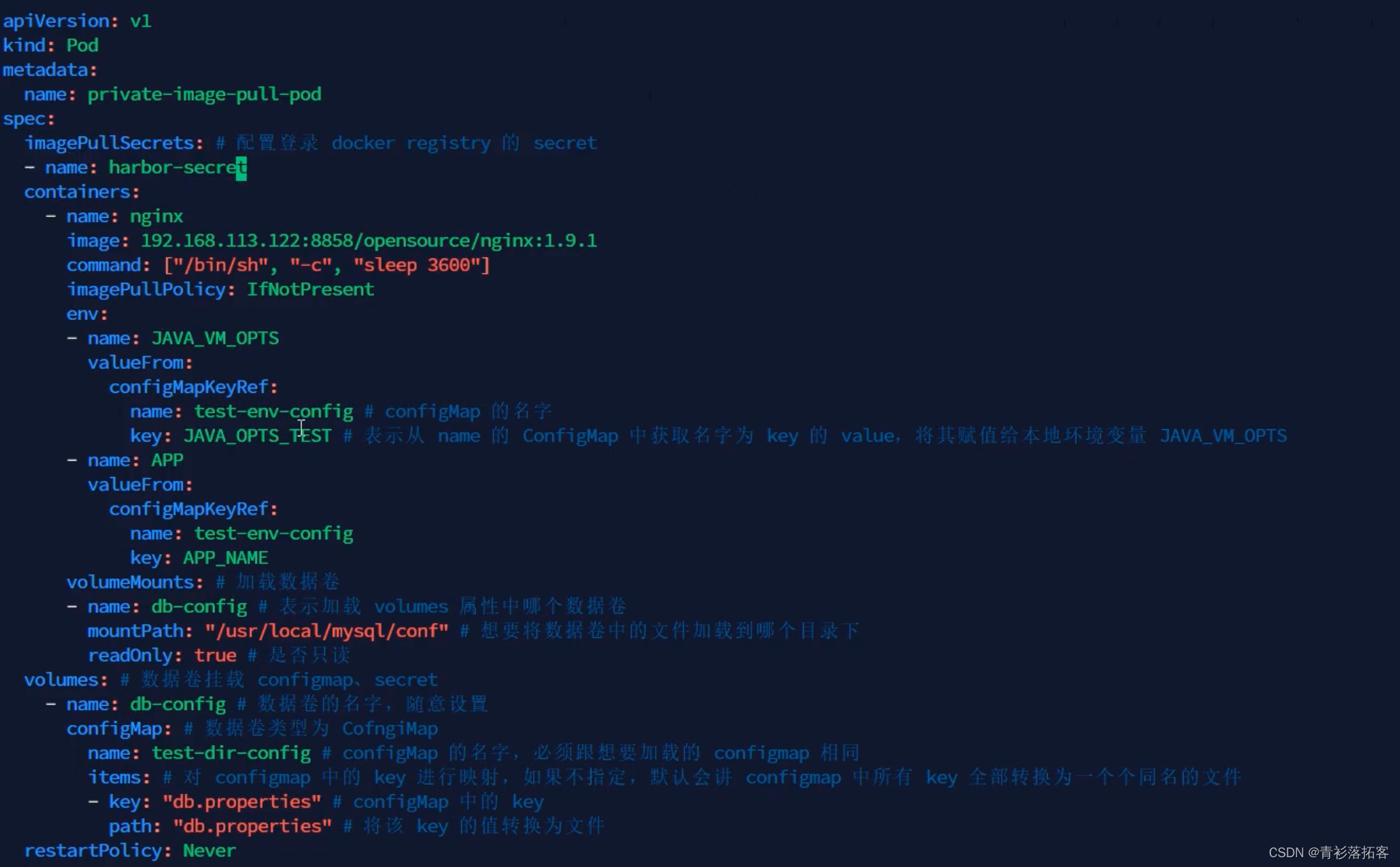
(五)k8s实战-配置管理
一、ConfigMap 使用 kubectl create configmap -h 查看示例,构建 configmap 对象 1) 基于文件夹,加载文件夹下所有配置文件,创建 kubectl create configmap <configmapName> --from-file<dirPath>2) 指定配置文件,创…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...
