回归分析扫盲:为什么非线性模型不能直接用最优子集选择法
最近有人给我发了篇文章:

一个问题有一堆变量,我们要选取哪些变量来建模呢?我们来看看这篇文章是怎么做的:

这个方法简单来说就是:对于这一堆变量,我们每次尝试剔除其中一个变量,然后用剩下的变量训练一个新模型。那么,少了一个变量,模型的效果就会有区别,这个区别就是该变量的贡献。最后,我们选出贡献比较大的那些变量,构成我们的最终模型。
这种认识明显是错的。举一个易懂的反例:我们都知道深度模型数据越多上限越高(也就是现在大家说的“涌现”),但同时数据越多也会导致训练难度越高——也就是说,用少量数据训练小模型,和用大量数据训练大模型,在不调参的情况下,很可能前者的效果远远超过后者——如果按这篇文章的说法,那推出的结果就是“大量数据是没用的”,这显然是错的。出现这种现象只是因为少量数据训练的小模型比大量数据训练的大模型下限更高而已。
我这么说之后,有个学经济的同学说我说的不对,这篇文章说的这个方法其实是经济学建模常用的方法“最优子集选择法”——如果你也这么认为,那就说明你既不懂数学上的函数拟合、也不懂经济学上的回归分析。首先,“最优子集选择法”不是用来干这件事的,其次,“最优子集选择法”也不能在这种模型上用。下面我来讲讲为什么。
为什么非线性模型不能用最优子集选择法
大部分人应该是在学习回归分析时接触的最优子集选择法——在使用线性模型进行回归分析时,用这个方法来剔除共线性的解释变量。为什么我们要发现并剔除共线性的变量?因为经济学模型的目的是解释现象,对于线性回归分析,就是要根据拟合后每个自变量的系数来解释它对响应变量的影响。但如果存在两个变量共线性,就会造成一个变量的系数可以被另一个变量吸收。比如A、B两个变量共线,那拟合之后的结果在极端情况可能是100A+0B或100B+0A——但这并不代表其中一个有超大的影响,另一个没有影响,只是因为一个变量的影响被另一个吸收了。对于这种结果,你是无法做出正确解释的。
在这个时候,我们就可以使用最优子集选择法:分别做一个有A无B的模型和有B无A的模型,发现这两个模型从参数到结果都很类似,只不过是第二个模型把第一个模型的A换成了B——这种情况就说明他俩共线性——A和B的背后有一个共同的隐变量,是这个隐变量在对响应变量施加影响。那么我可以继续研究这个隐变量到底是什么。或者分析A和B哪个与那个隐变量更相关,从而选取更好的解释变量。
但是非线性模型就不存在这个问题——你要想一想,为什么线性模型里两个共线变量的参数会互相吸收?这只是因为多项式分配律而已。而非线性模型不是这个多项式形式,所以不会直接出现变量间互相吸收的情况——一个好的非线性模型,即使参数A和参数B有一丁点不一样,它也能把这一丁点不一样分离出来,然后用于预测。所以,对于非线性模型,对预测没有帮助的充分条件是两个变量一模一样[1](这时你一定可以至少去除一个),而并非共线。
基于以上分析,我们再回来看为什么非线性模型不能用最优子集选择法——我前面说了,“最优子集选择法”不是用来干这件事的,这是因为最优子集选择法是在帮助我们排除影响解释的因素,而并非直接让预测结果更好。事实上,对于线性模型,即使解释变量间存在共线性,但只要这些变量都与响应变量线性相关(而没有把无关变量混杂进来),那么它们同时存在也对预测精度没有太大影响。因此使用最优子集选择法的根本目的不是提高预测精度,你也不应该用预测精度作为指标来比较不同的变量子集好坏。“最优子集选择法”也不能在这种模型上用,这是因为非线性模型不需要检测共线性,两个共线性的变量也可能给预测提供有用信息。同时,因为使用不同的变量子集时,模型的最优超参数是不同的,所以,你也不能在不调参的情况下比较两个变量子集的好坏(即本文最开始说的反例)。
为什么最优子集选择法在某些情况下可以提高预测精度
不过,虽然我说“最优子集选择法”不是用来提高预测精度的,因此不应该用预测精度作为指标来比较不同的变量子集好坏,但是很多学经济的同学在实践中确实在用该方法进行变量选择,并获得比较好的模型,这样做为什么可以work呢?
仔细看前文可以发现,我强调两个不同变量子集训练出的模型预测精度无法直接比较的原因是,两个模型的最优超参数是不同的,超参数决定了优化迭代的初值和动力学路径。在不调参的情况下,两个模型在训练时可能一个走的是径直向下的山路,一个走的是凹凸不平的丘陵,显然前者会更快收敛到更好的参数,获得更好的预测精度,但这只是因为二者在训练过程中所走的路径不同,并不能说明前者的数据比后者更好(没有控制变量)。
但是,广义线性模型的最小二乘损失均为凸函数,因此无论你把初值选择在哪个地方,它都会沿着梯度方向收敛到最优参数(事实上这个凸函数的最小值是可以解析求解的,我们平时都是把数据带入这个解析解,直接得到最优参数,不需要进行迭代),因此就消除了超参数这个无法控制的变量——给出一组数据,直接就能得到能达到最好预测精度的最优参数。在这种情况下,预测精度是可以一定程度上说明两组数据的好坏的。
但这是否说明最优子集选择法可以用来提高预测精度呢?我前面已经说了,在使用线性模型时,如果你选取的解释变量全部与响应变量线性相关,那么再用最优子集选择法不会对精度有影响——所以,一些经济学同学使用“最优子集选择法”进行“变量选择”的本质仅仅是使用试错的方法排除了一些相关性较弱的变量而已。事实上,你直接计算一下每个解释变量和响应变量间的线性相关系数,然后进行排除,也可以有类似的结果,而且计算次数还会更少……如果你刻舟求剑,发现这个方法在线性模型上“有效”,然后像这个作者一样在非线性模型上还想用,那就是完全错误了……
最后我吐槽一句:都3202年了,能不能别抱着中文论文不放了?你看这作者犯的错误,他明显就是那种把经济当文科学,基本不懂数学,拿着几个方法到处生搬硬套的——总看这种人的文章,你能有好果汁吃?
[1] T. Liu, S. Zhang and Q. Xiong, "Separated Model for Stopping Point Prediction of Autoregressive Sequence," 2023 IEEE 12th Data Driven Control and Learning Systems Conference (DDCLS), Xiangtan, China, 2023, pp. 799-803, doi: 10.1109/DDCLS58216.2023.10167110.
相关文章:

回归分析扫盲:为什么非线性模型不能直接用最优子集选择法
最近有人给我发了篇文章: 一个问题有一堆变量,我们要选取哪些变量来建模呢?我们来看看这篇文章是怎么做的: 这个方法简单来说就是:对于这一堆变量,我们每次尝试剔除其中一个变量,然后用剩下的变…...

单例模式简介
概念: 单例模式(Singleton Pattern)是一种创建型设计模式,它确保一个类只有一个实例,并提供全局访问点。单例模式的核心思想是限制某个类只能创建一个对象实例,并提供对该实例的全局访问。这样可以避免多个…...
WPF自定义命令及属性改变处理
1、项目建构 2、自定义命令 namespace WpfDemo.Base {public class MyCommand : ICommand{Action executeAction;public MyCommand(Action action){executeAction action;}public event EventHandler? CanExecuteChanged;public bool CanExecute(object? parameter){retu…...

macbook m1 docker中使用go
已经有一个centos8的镜像,本来打算在centos8中安装go 安装方法: # 1.下载go的安装包 mkdir install && cd install # 任意创建个文件夹 wget https://go.dev/dl/go1.20.2.linux-amd64.tar.gz# 2. 解压 tar -C xzf go1.20.2.linux-amd64.tar.g…...
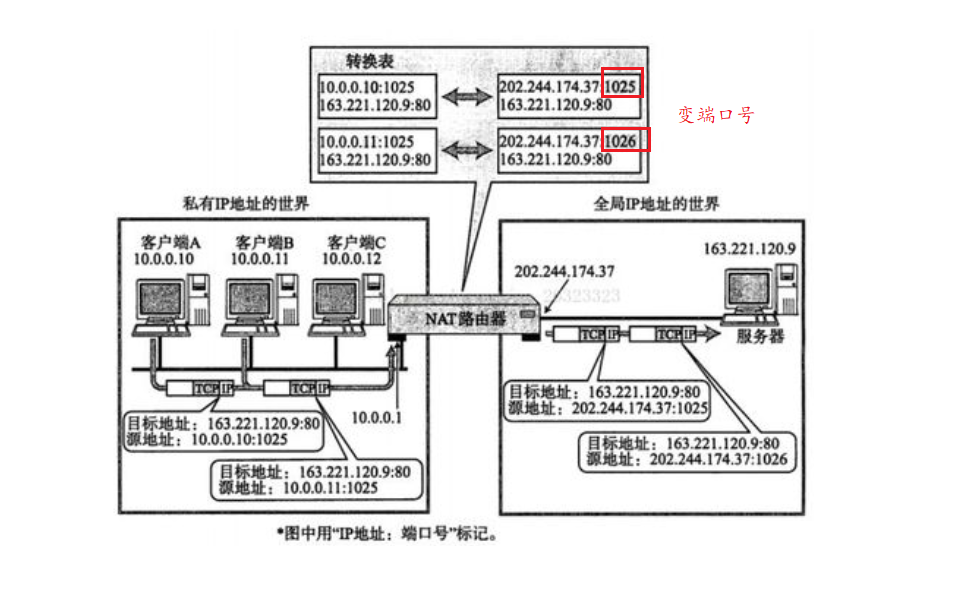
【Hello Network】DNS协议 NAT技术 代理服务器
本篇博客简介:介绍DNS协议 NAT技术和代理服务器 网络各协议补充 DNSDNS背景DNS介绍DNS总结域名简介 NAT技术NAT技术背景NAT IP转换过程NAPTNAT技术缺陷NAT和代理服务器 网络协议总结应用层传输层网络层数据链路层 DNS DNS是一整套从域名映射到IP的系统 DNS背景 为…...
Android 使用模拟器模拟Linux操作系统
1. 简介 在Android手机上使用模拟器模拟ubuntu等操作系统,便于测试 2. 软件准备 Termux:是一款 Android 终端模拟器和 Linux 环境应用程序,无需 root 或设置即可直接运行。虽然酷安和谷歌菜市场都能下载,但这些渠道都很久没更新…...

机器学习基础之《分类算法(5)—朴素贝叶斯算法原理》
一、朴素贝叶斯算法 1、什么是朴素贝叶斯分类方法 之前用KNN算法,分类完直接有个结果,但是朴素贝叶斯分完之后会出现一些概率值,比如: 这六个类别,它都有一定的可能性 再比如,对文章进行分类:…...

# Go学习-Day6
文章目录 Go学习-Day6封装继承接口 Go学习-Day6 个人博客:CSDN博客 封装 类似java的类的封装,这里我们利用大小写和工厂模式来实现封装的功能略过 继承 相似的类具有相似的方法,反复绑定相同的方法,代码冗余,所以引…...
分布式 - 服务器Nginx:一小时入门系列之 HTTPS协议配置
文章目录 1. HTTPS 协议2. 生成 SSL 证书和私钥文件3. 配置 SSL 证书和私钥文件4. HTTPS 协议优化 1. HTTPS 协议 HTTPS 是一种通过计算机网络进行安全通信的协议。它是HTTP的安全版本,通过使用 SSL 或 TLS 协议来加密和保护数据传输。HTTPS的主要目的是确保在客户…...

探秘Linux系统性能监控神器!Linux和Python技术持续学习者必看!
引言 作为Linux运维工程师,我们经常需要对服务器的性能进行监控和调优。而Python作为一门强大的脚本语言,可以帮助我们轻松实现各种系统性能监控任务。本文将介绍几个实用的Python库和工具,帮助我们监控Linux系统的CPU、内存、磁盘和网络等性…...

文心一言续写太监小说《名侦探世界的巫师》
《名侦探世界的巫师》是我的童年回忆,总是想着续写一下,但是又没有时间和文笔,文心一言出了,由于目前大模型貌似可以联网,可以尝试搞一波~ 目录 文章1【前六个故事还能看,后面就是在重复】故事2【辣眼睛】…...
)
Solidity 合约安全,常见漏洞(第三篇)
Solidity 合约安全,常见漏洞(第三篇) ERC20 代币问题 如果你只处理受信任的 ERC20 代币,这些问题大多不适用。然而,当与任意的或部分不受信任的 ERC20 代币交互时,就有一些需要注意的地方。 ERC20&#…...
Linux安装Redis数据库,无需公网IP实现远程连接
文章目录 1. Linux(centos8)安装redis数据库2. 配置redis数据库3. 内网穿透3.1 安装cpolar内网穿透3.2 创建隧道映射本地端口 4. 配置固定TCP端口地址4.1 保留一个固定tcp地址4.2 配置固定TCP地址4.3 使用固定的tcp地址连接 Redis作为一款高速缓存的key value键值对的数据库,在…...

智慧政务,长远布局——AIGC引领,加速推进数字化政府建设
在人工智能、虚拟现实等领域迅猛发展且日益成熟的背景下,AI行业正迈向蓬勃发展的全新阶段,市场规模持续扩张。与此同时,数字服务也正在蓬勃兴起,新一代信息技术为数字政府构建了坚实支撑,重塑了政务信息化管理、业务架…...
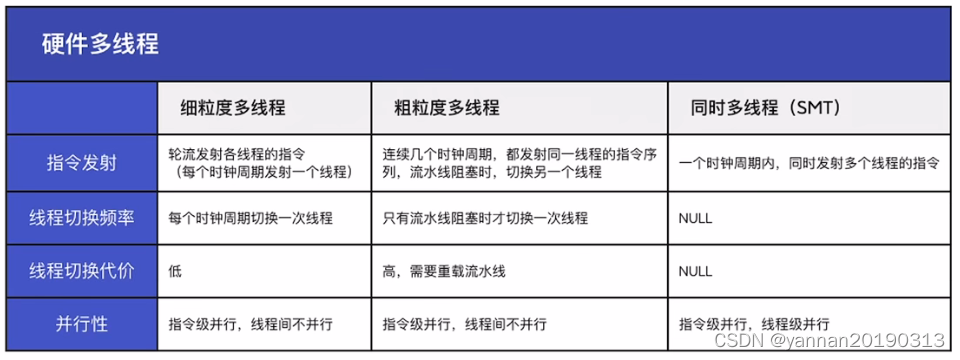
中央处理器(CPU):组成、指令周期、数据通路、控制方式、控制器、指令流水线,补充(多处理器系统、硬件多线程)
中央处理器(CPU,Central Processing Unit),计算机控制和运算的核心,是信息处理和程序运行的执行单元。 CPU主要功能:处理指令、执行操作、控制时间、处理中断、处理数据。 其中,处理指令、执行…...

开源微服务如何选型?Spring Cloud、Dubbo、gRPC、Istio 详细对比
作者:刘军 不论您是一名开发者、架构师、CTO, 如果您曾深度参与在微服务开发中,那么相信您一定有过开源微服务框架或体系选型的疑问:Apache Dubbo、Spring Cloud、gRPC 以及 Service Mesh 体系产品如 Istio,到底应该选…...

Nginx的HTTPS部署与安全性能优化
Nginx作为一款高性能的Web服务器和反向代理服务器,被广泛用于应用部署和负载均衡。在安全环保意识的逐渐提高下,HTTPS也成为现代Web应用中必不可少的一环。本篇文章将重点介绍Nginx的HTTPS部署和安全性能优化。 一、Nginx的HTTPS部署 证书申请 首先需要去…...

5.8. Trusted Board Boot
5.8. Trusted Board Boot启动 Trusted Board Boot(TBB) 功能通过验证所有固件镜像(包括正常世界引导加载程序)来防止恶意固件在平台上运行。它通过使用公钥加密标准 (PKCS) 建立信任链来实现这一点。 本文介绍了可信固件-A (TF-A) TBB 的设计,它是Trusted Board Boot(TBBR…...

微信小程序——van-field中的left-icon属性自定义
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...

一文学会lua脚本
文章目录 0.前言背景应用 1. 学习大纲1. 学习基本语法:2. 理解函数和模块:3. 深入数据结构:4. 高级特性和技巧:5. 实践项目: 2. Lua脚本2.1 学习基本语法2.2 理解函数和模块2.3 深入数据结构2.4 高级特性和技巧 3. 高级…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...

ubuntu22.04 安装docker 和docker-compose
首先你要确保没有docker环境或者使用命令删掉docker sudo apt-get remove docker docker-engine docker.io containerd runc安装docker 更新软件环境 sudo apt update sudo apt upgrade下载docker依赖和GPG 密钥 # 依赖 apt-get install ca-certificates curl gnupg lsb-rel…...

大数据治理的常见方式
大数据治理的常见方式 大数据治理是确保数据质量、安全性和可用性的系统性方法,以下是几种常见的治理方式: 1. 数据质量管理 核心方法: 数据校验:建立数据校验规则(格式、范围、一致性等)数据清洗&…...
