CF 148 D Bag of mice(概率dp求概率)
CF 148 D. Bag of mice(概率dp求概率)
Problem - 148D - Codeforces
大意:袋子里有 w 只白鼠和 b 只黑鼠 ,A和B轮流从袋子里抓,谁先抓到白色谁就赢。A每次随机抓一只,B每次随机抓完一只之后会有另一只随机老鼠跑出来。如果两个人都没有抓到白色则B赢。A先抓,问A赢的概率。
思路:看到数据范围后考虑 概率dp , 设 dp[i][j] 为有 i 个白鼠 j 个黑鼠 A先手获胜的概率
考虑初始化
i == 0 全是黑鼠 , A 必败
dp[i][j] == 0
j == 0 全是白鼠 , A 必胜
dp[i][j] == 1
分情况考虑转移
分四种情况:
1. A 取到白鼠 dp[i][j] += i / (i + j)
2. A 取到黑鼠 , B取到白鼠 dp[i][j] += 0;
3. A 取到黑鼠 , B取到黑鼠 , 白鼠跑出来 dp[i][j] += j / (i + j) * (j - 1) / (i + j - 1) * i / (i + j - 2) * dp[i - 1][j - 2]
4. A 取到黑鼠 , B取到黑鼠 , 黑鼠跑出来 dp[i][j] += j / (i + j) * (j - 1) / (i + j - 1) * (j - 2) / (i + j - 2) * dp[i][j - 3]
#include<bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define int long long
const int N = 1e3 + 10;
const int mod = 1e9 + 7;
typedef pair<int,int>PII;double dp[N][N];
int x , y;inline double pro(int x , int y){return (double) x / (double) y;
}signed main(){IOScout << fixed << setprecision(10);cin >> x >> y;for(int i = 1 ; i <= x ; i ++) dp[i][0] = 1;for(int i = 1 ; i <= y ; i ++) dp[0][i] = 0;for(int i = 1 ; i <= x ; i ++){for(int j = 1 ; j <= y ; j ++){dp[i][j] += pro(i , i + j);if(i >= 1 && j >= 2) dp[i][j] += pro(j , i + j) * pro(j - 1 , i + j - 1) * pro(i , i + j - 2) * dp[i - 1][j - 2];if(j >= 3) dp[i][j] += pro(j , i + j) * pro(j - 1 , i + j - 1) * pro(j - 2 , i + j - 2) * dp[i][j - 3];}}cout << dp[x][y];return 0;
}
//freopen("文件名.in","r",stdin);
//freopen("文件名.out","w",stdout);
相关文章:
)
CF 148 D Bag of mice(概率dp求概率)
CF 148 D. Bag of mice(概率dp求概率) Problem - 148D - Codeforces 大意:袋子里有 w 只白鼠和 b 只黑鼠 ,A和B轮流从袋子里抓,谁先抓到白色谁就赢。A每次随机抓一只,B每次随机抓完一只之后会有另一只随机老鼠跑出来。如果两个人…...

引入本地 jar 包教程
将本地 jar 包,放到 resource 目录下,在 pom.xml 文件中加入如下依赖: <dependency><groupId>com.hk</groupId><artifactId>examples</artifactId><version>1.0</version><scope>system<…...
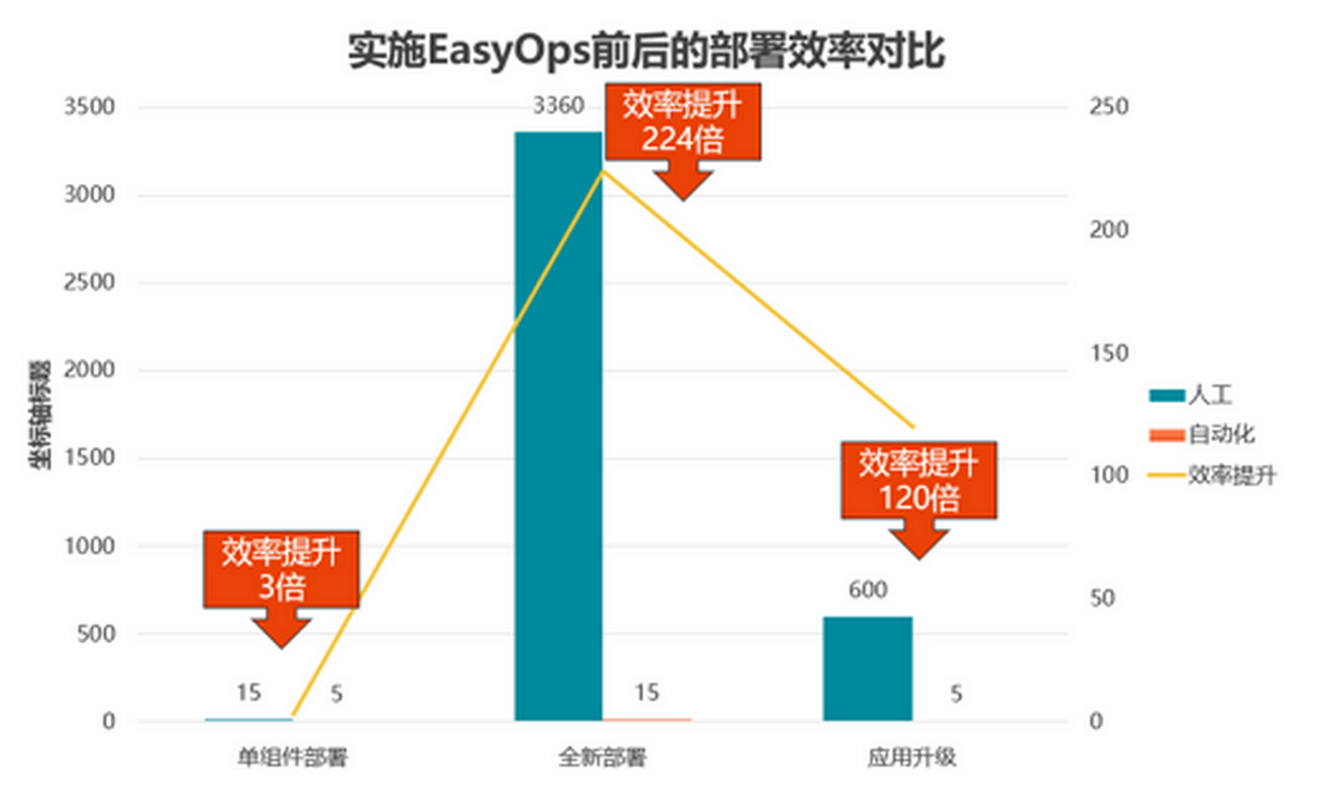
优维产品最佳实践第5期:什么是持续集成?
谈到到DevOps,持续交付流水线是绕不开的一个话题,相对于其他实践,通过流水线来实现快速高质量的交付价值是相对能快速见效的,特别对于开发测试人员,能够获得实实在在的收益。 本期EasyOps产品使用最佳实践,…...
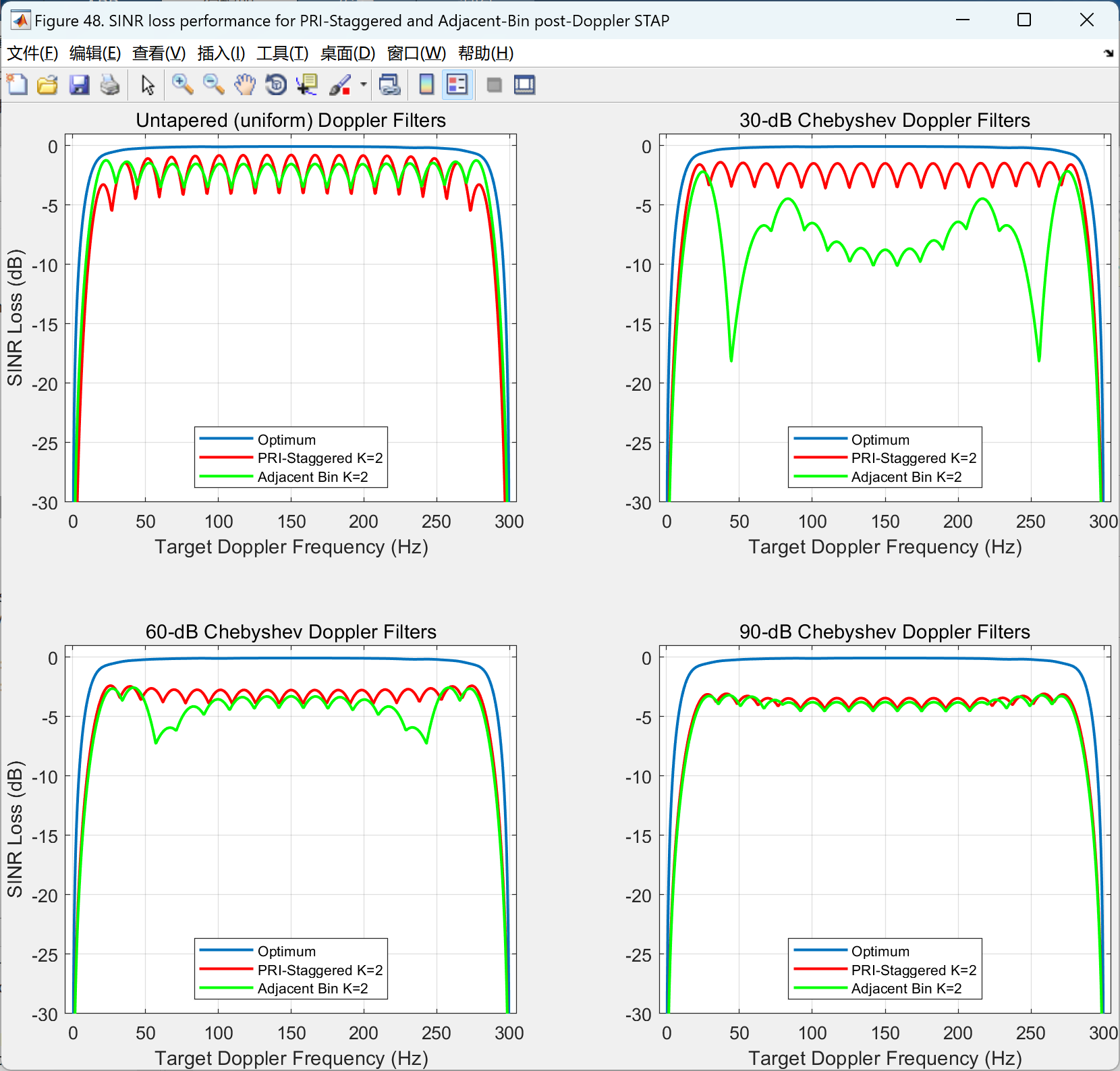
空时自适应处理用于机载雷达——元素空间空时自适应处理(Matla代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

聚观早报 | 青瓷游戏上半年营收3.34亿元;如祺出行冲击IPO
【聚观365】8月26日消息 青瓷游戏上半年营收3.34亿元 如祺出行冲击IPO 索尼互动娱乐将收购Audeze 昆仑万维上半年净利润3.6亿元 T-Mobile计划在未来五周内裁员5000人 青瓷游戏上半年营收3.34亿元 青瓷游戏发布截至2023年6月30日止的中期业绩,财报显示…...

硅谷的魔法:如何塑造了全球技术的未来
硅谷的创新文化简介 硅谷,位于美国加利福尼亚州的圣克拉拉谷,已经从一个半导体产业的中心发展成为全球技术创新的代名词。这里集结了全球最顶尖的技术公司、创业者和投资者,共同创造了一个技术创新的奇迹。 起源与发展 硅谷的起源与斯坦福大…...
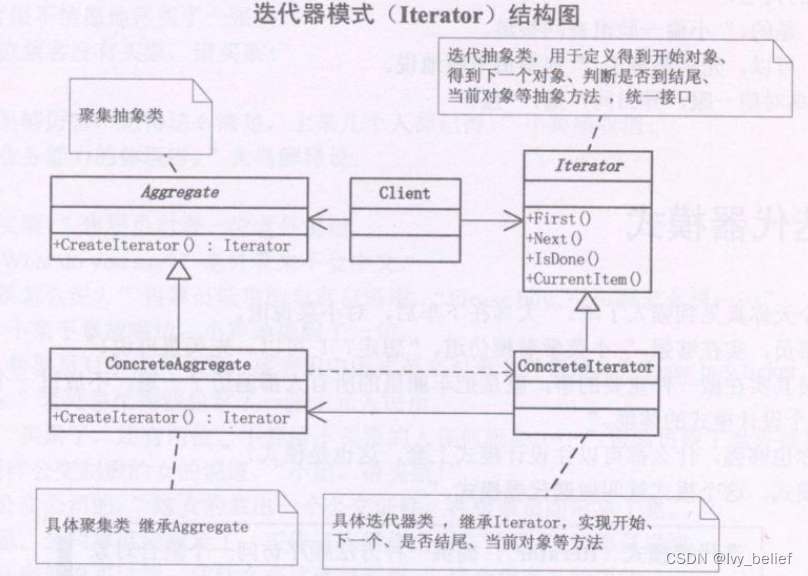
(三)行为模式:4、迭代器模式(Iterator Pattern)(C++示例)
目录 1、迭代器模式(Iterator Pattern)含义 2、迭代器模式的UML图学习 3、迭代器模式的应用场景 4、迭代器模式的优缺点 (1)优点 (2)缺点 5、C实现迭代器模式的实例 1、迭代器模式(Itera…...
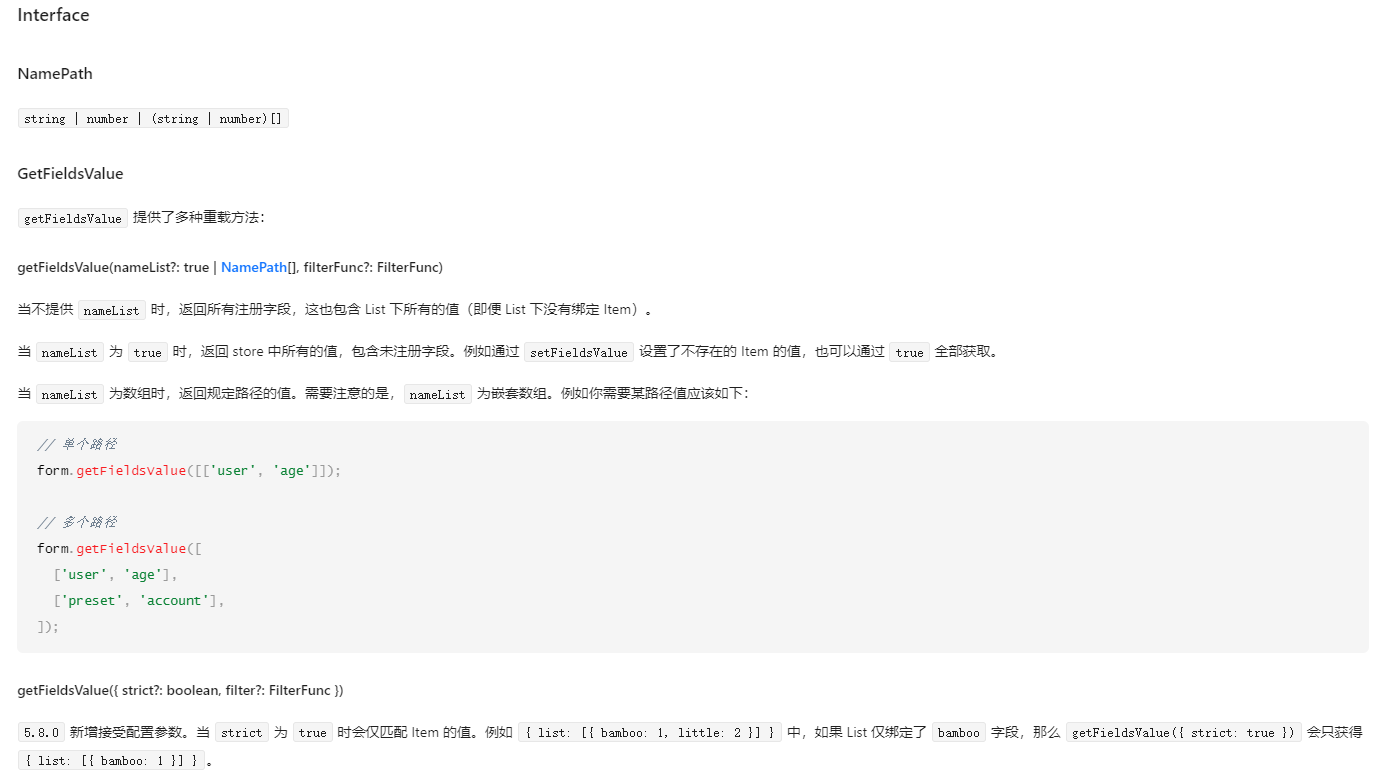
React Antd form.getFieldsValue() 和 form.getFieldsValue(true) 有区别吗?
背景 突然发现 antd 的 getFieldsValue()是可以传一个 true 参数的,如题,React Antd form.getFieldsValue() 和 form.getFieldsValue(true) 有区别吗? 验证 确实不一样 结论 getFieldsValue 提供了多种重载方法: getFieldsValue(name…...

浅谈Java中的观察者模式
观察者模式是软件开发中常用的一种设计模式,它通过定义一对多的依赖关系,使得一个对象(主题)的状态变化可以通知多个其他对象(观察者)。 这种模式的优点是解耦和增加扩展性,用于实现对象之间的…...

C++:命名空间,缺省参数,函数重载,引用,内联函数
个人主页 : 个人主页 个人专栏 : 《数据结构》 《C语言》《C》 文章目录 前言一、命名空间命名空间的定义命名空间的使用 二、缺省参数缺省参数概念缺省参数分类 三、函数重载函数重载的概念 四、引用引用的概念引用特性引用的使用场景引用与指针的区别 …...
)
2.Vue报错Cannot read properties of undefined (reading ‘then‘)
1.出现报错 Cannot read properties of undefined (reading ‘then’), 代码为 uploadFile(e.target.files[0]).then((res) > {alert(JSON.stringify(res));});2.原因 是因为uploadFile方法没有返回值,于是我又检查了一遍代码,发现我的r…...

【LeetCode 】数组简介
集合列表和数组 本文中介绍的概念为适用于所有编程语言的抽象理论,具体实现会由编程语言的不同而稍有差别。 具体介绍数组之前,我们先来了解一下集合、列表和数组的概念之间的差别。 集合 集合一般被定义为:由一个或多个确定的元素所构成的…...

一文解析block io生命历程
作为存储业务的一个重要组成部分,block IO是非易失存储的唯一路径,它的生命历程每个阶段都直接关乎我们手机的性能、功耗、甚至寿命。本文试图通过block IO的产生、调度、下发、返回的4个阶段,阐述一个block IO的生命历程。 一、什么是块设备…...

Python爬虫学习之旅:从入门到精通,要学多久?
导语: 随着信息时代的发展,大量的数据和信息储存在互联网上,这为我们提供了获取和利用这些数据的机会。而Python爬虫作为一种强大的工具,可以帮助我们从网页中提取数据,并进行进一步的分析和挖掘。然而,对…...
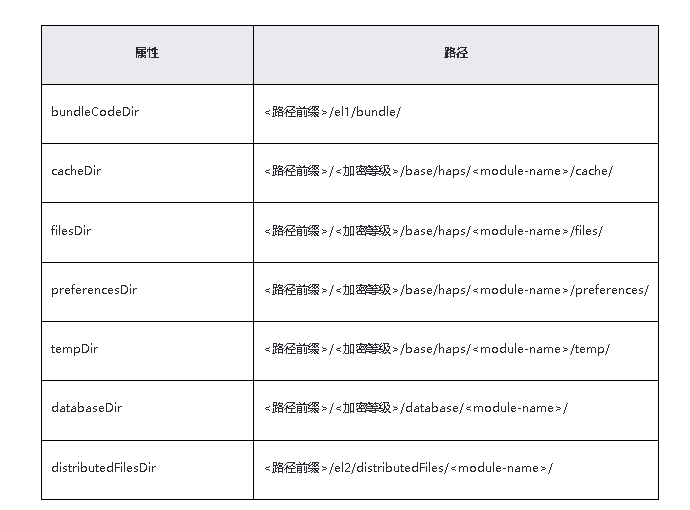
HarmonyOS/OpenHarmony(Stage模型)卡片开发应用上下文Context使用场景一
1.获取应用文件路径 基类Context提供了获取应用文件路径的能力,ApplicationContext、AbilityStageContext、UIAbilityContext和ExtensionContext均继承该能力。应用文件路径属于应用沙箱路径。上述各类Context获取的应用文件路径有所不同。 通过ApplicationContext…...
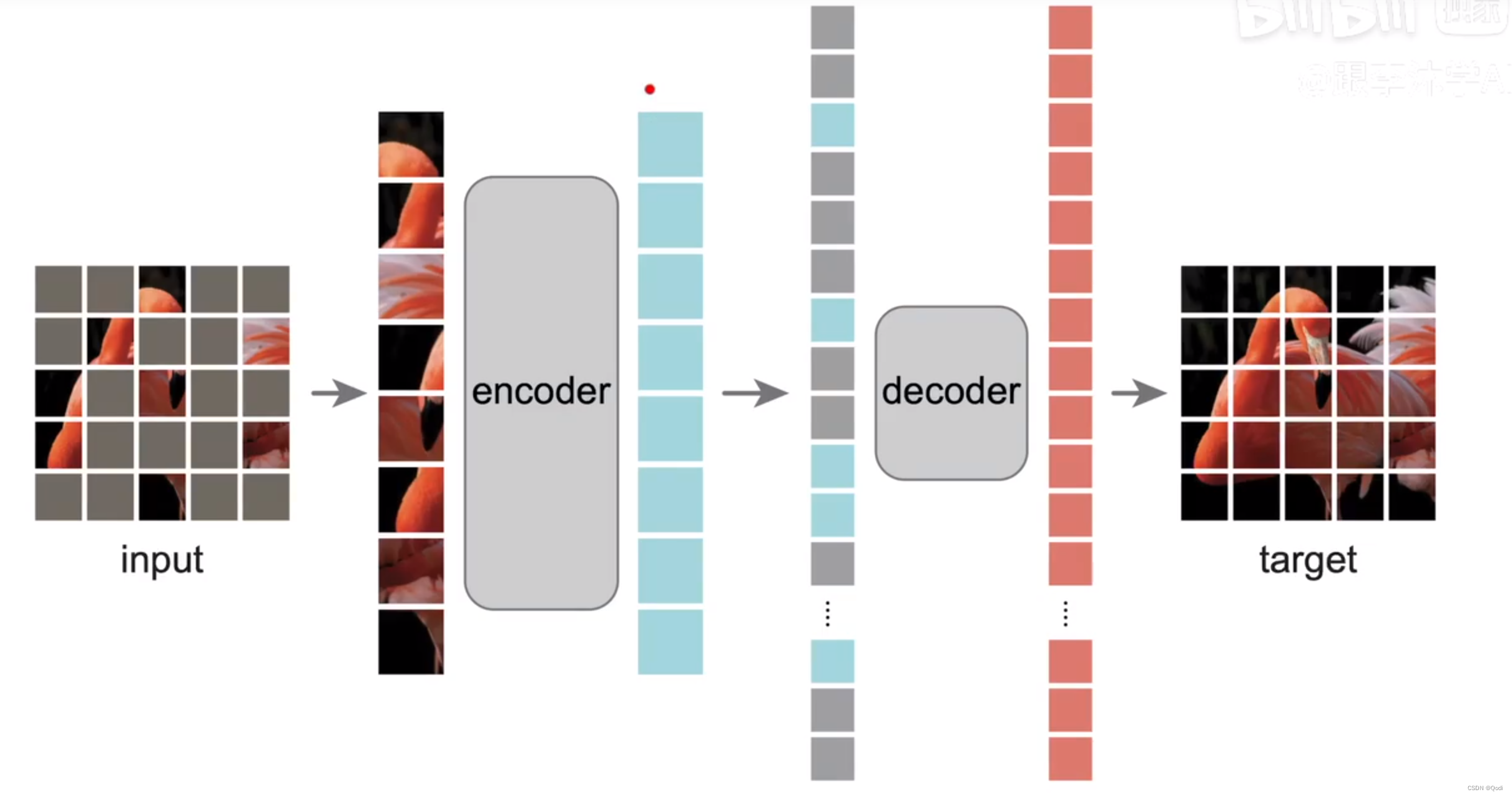
MAE 论文精读 | 在CV领域自监督的Bert思想
1. 背景 之前我们了解了VIT和transformer MAE 是基于VIT的,不过像BERT探索了自监督学习在NLP领域的transformer架构的应用,MAE探索了自监督学习在CV的transformer的应用 论文标题中的Auto就是说标号来自于图片本身,暗示了这种无监督的学习 …...

C++中内存的分配
一个由C/C编译的程序占用的内存分为以下几个部分 1、栈区(stack)— 由编译器自动分配释放 ,存放函数的参数值,局部变量的值等。 2、堆区(heap) — 一般由程序员分配释放, 若程序…...

Qt中的垂直布局QVBoxLayout和水平布局QHBoxLayout
文章目录 QVBoxLayoutQHBoxLayout QVBoxLayout Qt中的垂直布局(Vertical Layout)是用来将控件按垂直方向进行排列的布局管理器。下面是一些常用的Qt Vertical Layout的函数及其用法示例: QVBoxLayout类的构造函数: QVBoxLayout…...

【C#学习笔记】委托和事件
文章目录 委托委托的定义委托实例化委托的调用多播委托 为什么使用委托?官方委托泛型方法和泛型委托 事件为什么要有事件?事件和委托的区别: 题外话——委托与观察者模式 委托 在 .NET 中委托提供后期绑定机制。 后期绑定意味着调用方在你所…...

堆排序简介
概念: 堆排序是一种基于二叉堆数据结构的排序算法。它的概念是通过将待排序的元素构建成一个二叉堆,然后通过不断地取出堆顶元素并重新调整堆的结构来实现排序。 算法步骤: 构建最大堆(或最小堆):将待排…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...

DiscuzX3.5发帖json api
参考文章:PHP实现独立Discuz站外发帖(直连操作数据库)_discuz 发帖api-CSDN博客 简单改造了一下,适配我自己的需求 有一个站点存在多个采集站,我想通过主站拿标题,采集站拿内容 使用到的sql如下 CREATE TABLE pre_forum_post_…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现指南针功能
指南针功能是许多位置服务应用的基础功能之一。下面我将详细介绍如何在HarmonyOS 5中使用DevEco Studio实现指南针功能。 1. 开发环境准备 确保已安装DevEco Studio 3.1或更高版本确保项目使用的是HarmonyOS 5.0 SDK在项目的module.json5中配置必要的权限 2. 权限配置 在mo…...
32单片机——基本定时器
STM32F103有众多的定时器,其中包括2个基本定时器(TIM6和TIM7)、4个通用定时器(TIM2~TIM5)、2个高级控制定时器(TIM1和TIM8),这些定时器彼此完全独立,不共享任何资源 1、定…...
