【电能质量扰动】基于ML和DWT的电能质量扰动分类方法研究(Matlab实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码实现
💥1 概述
近年来,随着可再生能源的并网以及非线性负载和固态开关器件的数量不断增加,导致了大量严重
的电能质量问题。同时,精密电子设备的广泛使用需要极高质量的电源。为合理有效地改善电能质量,电能质量扰动问题的准确分类也变得非常重要 [1]。目前电能质量扰动问题分类方法的过程主要包括特征提取和模式识别两个步骤 [1]。特征提取常用的信息处理技术有短时傅里叶变换 (STFT)[2]、经验模态分解 ( E M D )[3] 和 S 变换 [4] 等。这些方法拥有很好的扰动识别效果,但也存在一些固有的缺陷。其中短时傅里叶变换的使用缺少可变窗口,不利于分析非平稳信号 ;S 变换是小波变换和短时傅里叶变换的结合,但其难点在于如何确认窗函数的宽度[4] ;经验模态分解存在严重的模态混叠和端点效应问题。离散小波变换 (DWT) 可以优化分解频率子带内的信号并估计扰动幅度,是一种灵活的扰动识别方法 [5]。因此,将 DWT 算法应用于特征提取。
模式识别常采用的方法有人工神经网络 [6]、决策树 [7] 和专家系统 [8] 等。人工神经网络存在容易陷入局部最优、收敛性较差等缺点 ;决策树容易出现过拟合现象和局部最优问题 ;专家系统由于自身不具备学习能力,所有的知识和解决方案都是由领域内的专家提供,因此其容错能力差,易产生组合爆炸的问题。支持向量机 (SVM) 基于小样本统计学习理论和结构风险最小化原理,具有较好的泛化能力 [9]。
D W T 具有非常有效的算法和稀疏表示,尤其在处理非平稳信号方面,具有良好的时频特性,和傅
里叶变换不同,离散小波分析不是根据三角多项式而是通过母小波函数的扩张和平移特性生成 [10]。信号h(t) 的 DWT 表示为 :
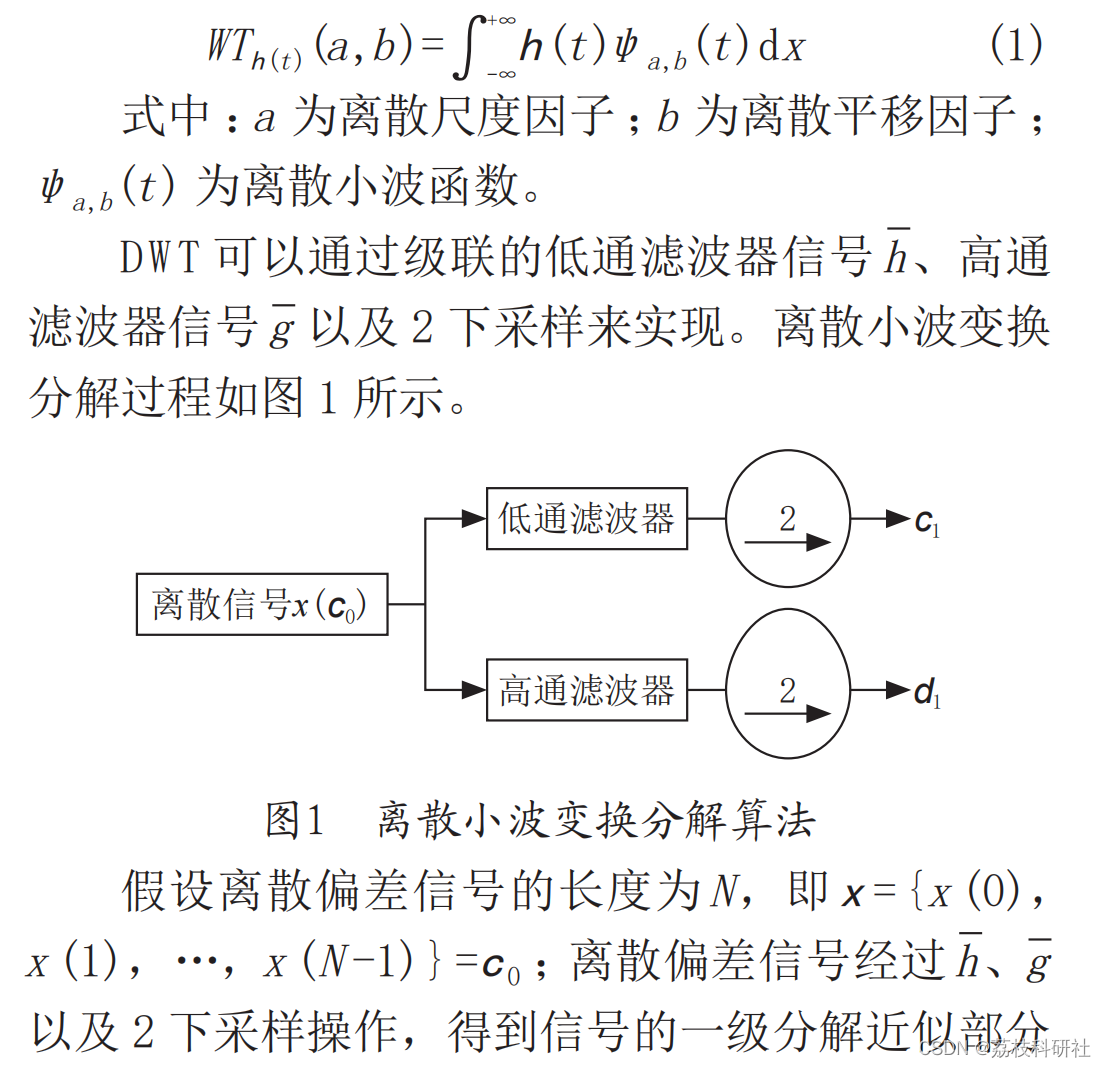

📚2 运行结果
运行视频:
基于ML和DWT的电能质量扰动分类方法研究(Matlab实现)_哔哩哔哩_bilibili

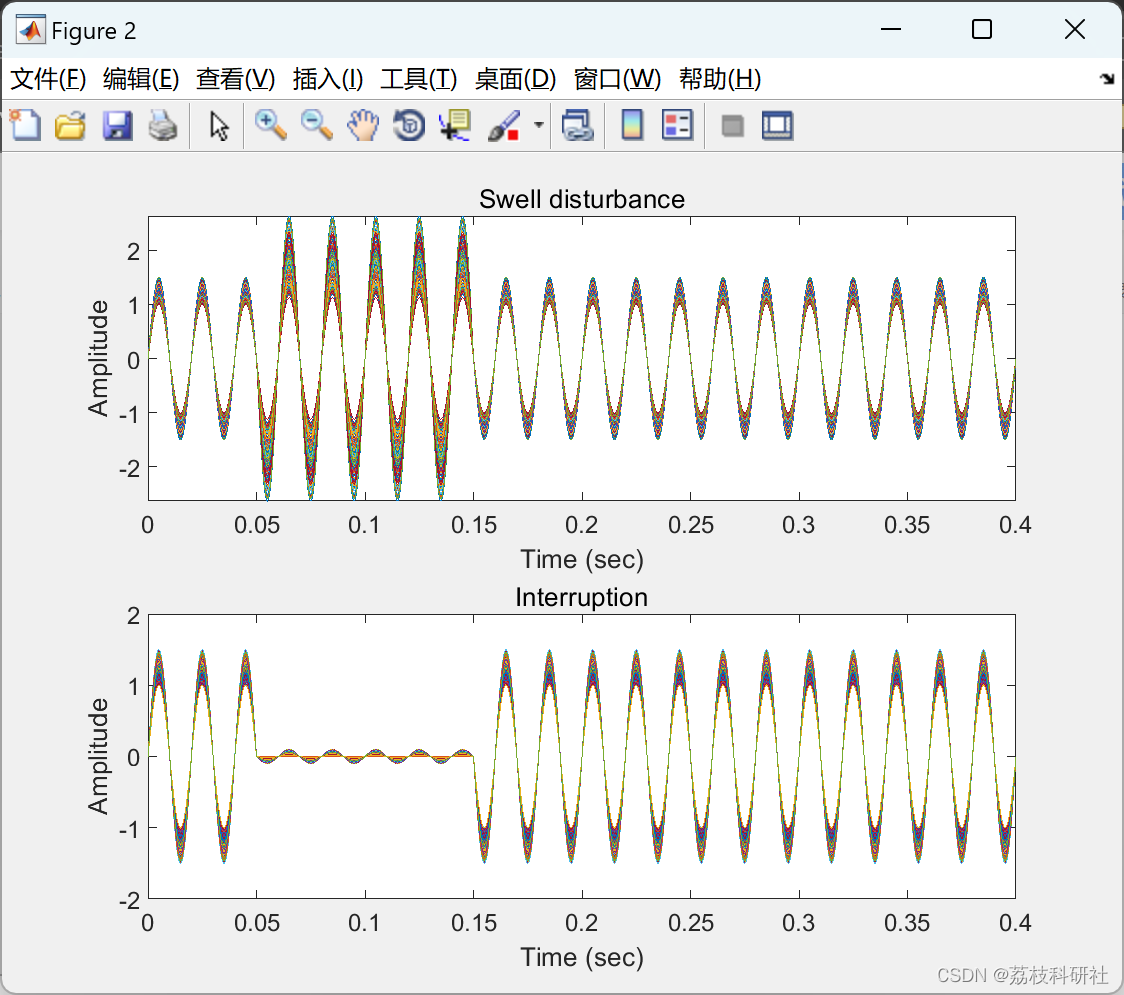
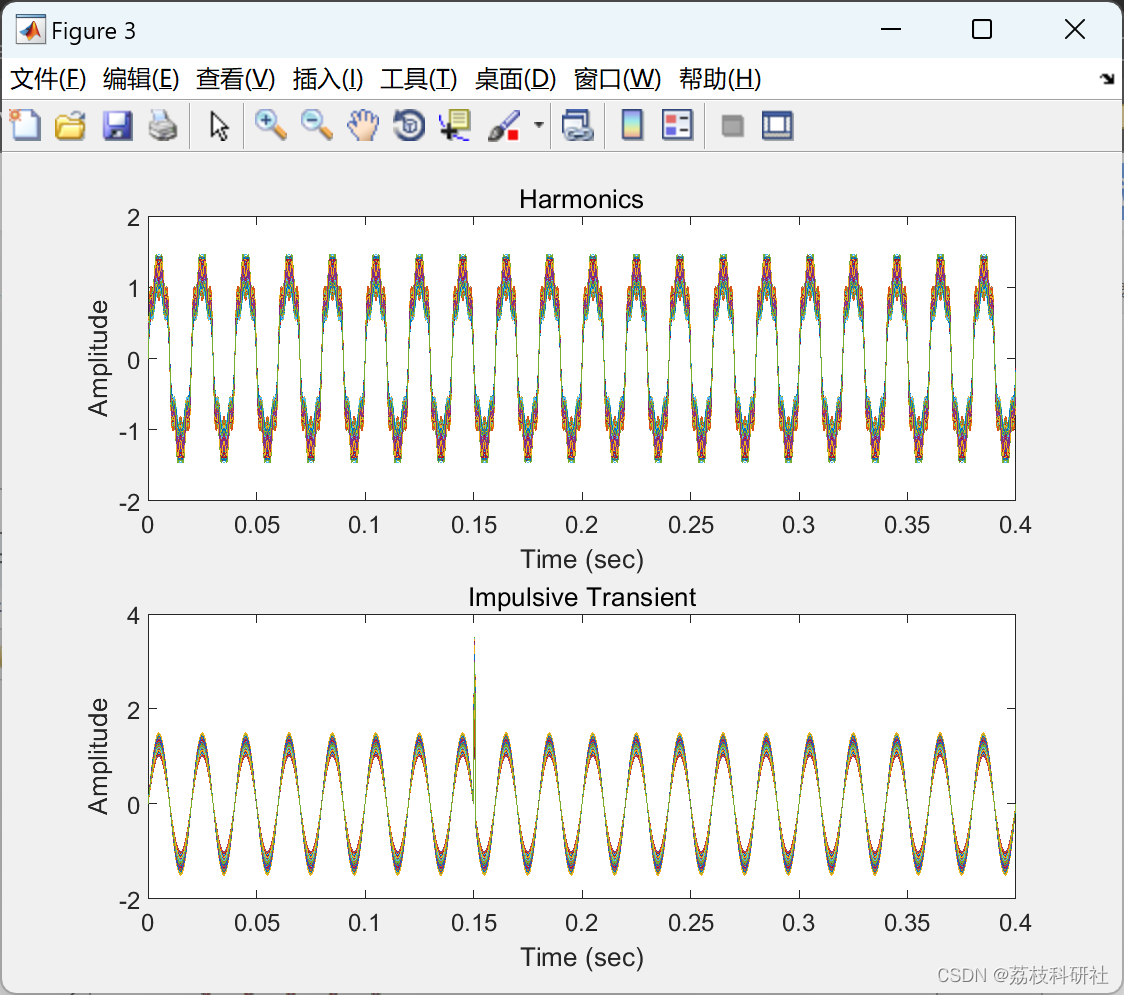
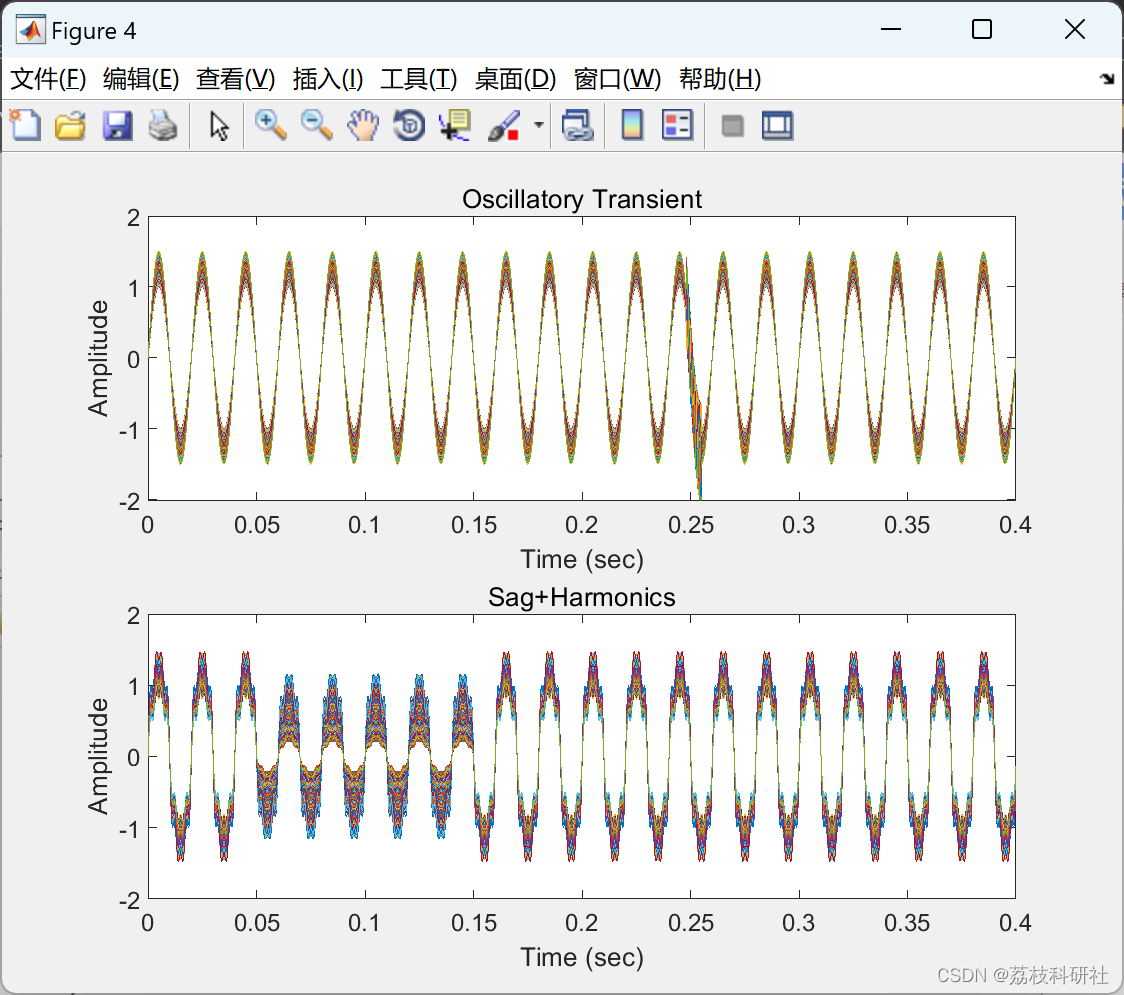
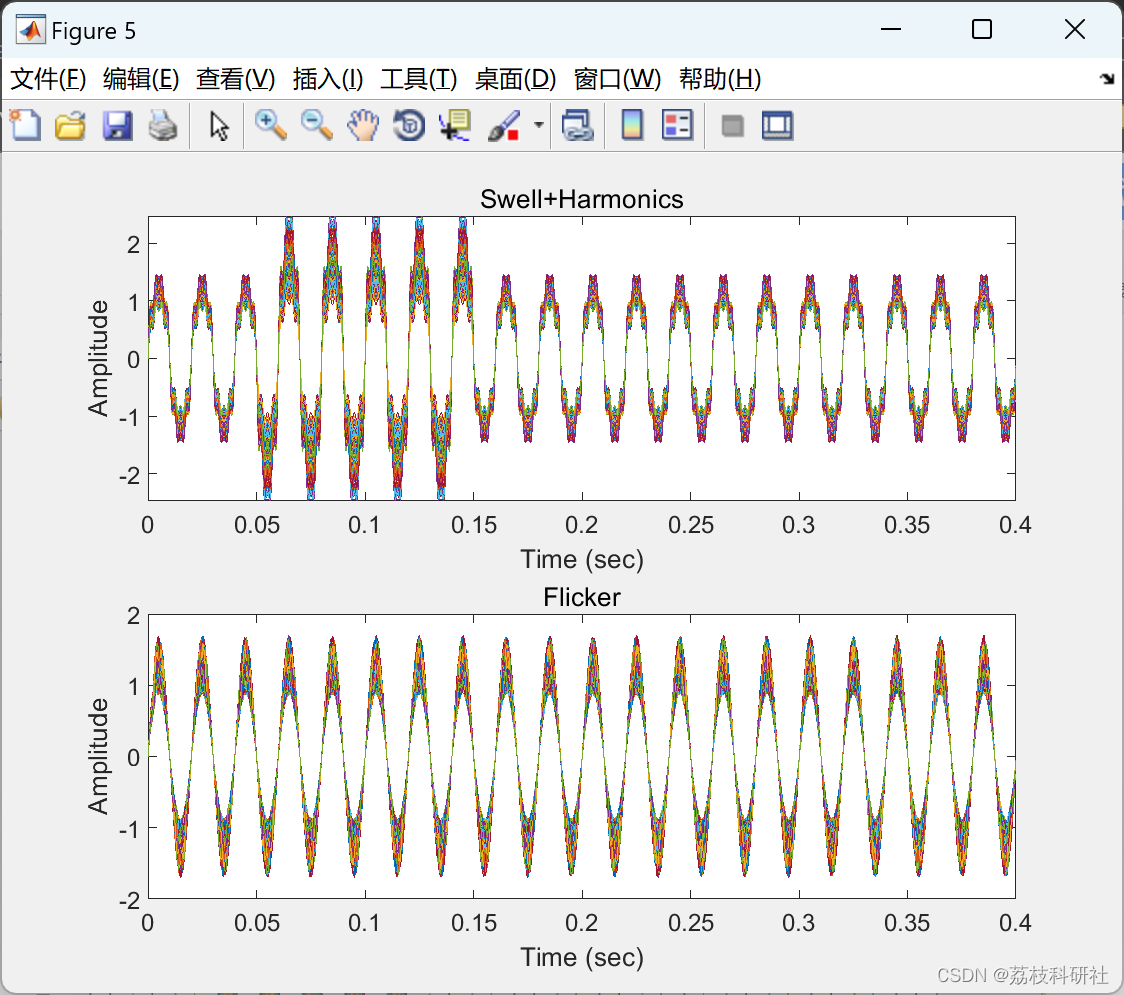 部分代码:
部分代码:
%% 暂态脉冲
%fn goes from 300 to 900
fn=500;
amp= rand(1,1)*range([4 7])+min([4 7]);
t1=0.151;
t2=0.150;
ty= (t1+t2)/2;
t=[0 :0.0001:0.4];
k=rand(1,1)*range([1 1.5])+min([1 1.5]);
y= k*(sin((2*pi*50)*t)+ amp*(heaviside(t-t2)-heaviside(t-t1)).*exp(-t/ty).*sin(2*pi*fn*t));
subplot(2,1,2);
plot(t,y)
title('Impulsive Transient');
xlabel ('Time (sec)');
ylabel ('Amplitude');
hold on
Impulsive_transient=[t,y]';
%% 振荡瞬态
%fn goes from 300 to 900
fn=rand(1,1)*range([300 500])+min([300 500]);
t=[0 :0.0001:0.4];
amp= 1;
t1=0.255;
t2=0.248;
ty= (t1+t2)/2;
t=[0 :0.0001:0.4];
k=rand(1,1)*range([1 1.5])+min([1 1.5]);
y= k*(sin((2*pi*50)*t)+ amp*(heaviside(t-t2)-heaviside(t-t1)).*exp(-t/ty).*sin((2*pi*fn)*t));
figure(4)
subplot(2,1,1);
plot(t,y)
title('Oscillatory Transient');
xlabel ('Time (sec)');
ylabel ('Amplitude');
hold on
Oscillatory_transient=[t,y]';
%% SAG+HARMONIC
t=[0 :0.0001:0.4];
alpha=rand(1,1)*range([0.1 0.8])+min([0.1 0.8]);
alpha3=rand(1,1)*range([0.05 0.15])+min([0.05 0.15]);
alpha5=rand(1,1)*range([0.05 0.15])+min([0.05 0.15]);
alpha7=rand(1,1)*range([0.05 0.15])+min([0.05 0.15]);
alpha1= sqrt(1- alpha3^2-alpha5^2-alpha7^2);
k=rand(1,1)*range([1 1.5])+min([1 1.5]);
y=k*((1-alpha*((heaviside(t-0.05)-heaviside(t-0.15)))).*(alpha1* sin(314*t)+ alpha3*sin(3*314*t)+ alpha5*sin(5*314*t)+ alpha7*sin(7*314*t)));
subplot(2,1,2);
plot(t,y);
title('Sag+Harmonics');
xlabel ('Time (sec)');
ylabel ('Amplitude');
hold on
Sag_harmonic=[t,y]';
%% SWELL+HARMONIC
t=[0 :0.0001:0.4];
alpha=rand(1,1)*range([0.1 0.8])+min([0.1 0.8]);
alpha3=rand(1,1)*range([0.05 0.15])+min([0.05 0.15]);
alpha5=rand(1,1)*range([0.05 0.15])+min([0.05 0.15]);
alpha7=rand(1,1)*range([0.05 0.15])+min([0.05 0.15]);
alpha1= sqrt(1-alpha3^2-alpha5^2-alpha7^2);
k=rand(1,1)*range([1 1.5])+min([1 1.5]);
y=k*((1+alpha*((heaviside(t-0.05)-heaviside(t-0.15)))).*(alpha1* sin(314*t)+ alpha3*sin(3*314*t)+ alpha5*sin(5*314*t)+ alpha7*sin(7*314*t)));
figure(5)
subplot(2,1,1);
plot(t,y)
title('Swell+Harmonics');
xlabel ('Time (sec)');
ylabel ('Amplitude');
hold on
Swell_harmonic=[t,y]';
%% FLICKER
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1]李家俊,吴建军,陈武,钟建伟.基于DWT-PCA-LIBSVM的电能质量扰动分类方法[J].电工电气,2023(03):20-24.
[2]马嘉秀,徐玮浓,何复兴,邵诗韵,赵家乐,李宁.基于WT和SVM的电能质量分类识别方法[J].智慧电力,2019,47(03):16-22+37.
🌈4 Matlab代码实现
相关文章:

【电能质量扰动】基于ML和DWT的电能质量扰动分类方法研究(Matlab实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

使用 OpenAI GPT 模型的最佳实践
推荐:使用NSDT场景编辑器助你快速搭建可二次编辑的3D应用场景 为了帮助用户获得最佳输出,OpenAI 提供了使用 GPT 模型的最佳实践。这来自体验,因为许多用户不断尝试使用此模型并找到了最有效的方法。 在本文中,我将总结使用 Ope…...
解除用户账户控制提醒
解决用户账户控制提醒 1. 前言2. 解决用户账户控制提醒2.1 控制面板2.2 注册表2.3 UAC服务 结束语 1. 前言 当我们使用电脑时,有时进行安装应用或者打开应用时,总会弹出一个提示框,要选择点击是否允许程序运行; 系统经常弹出用户…...
行业追踪,2023-08-23
自动复盘 2023-08-23 凡所有相,皆是虚妄。若见诸相非相,即见如来。 k 线图是最好的老师,每天持续发布板块的rps排名,追踪板块,板块来开仓,板块去清仓,丢弃自以为是的想法,板块去留让…...

算法修炼Day60|● 84.柱状图中最大的矩形
LeetCode:84.柱状图中最大的矩形 84. 柱状图中最大的矩形 - 力扣(LeetCode) 1.思路 双指针思路,以当前数组为中心,借助两个数组存放当前数柱左右两侧小于当前数柱高度的索引,进行h*w的计算。注意首尾节点的左侧索引…...
)
前端面试题css(一)
题目 盒子垂直水平居中如何实现text-align:center vertical-align: middle水平垂直居中布局positionmargin水平垂直居中布局 grid栅格化布局及其兼容性介绍一下BFC触发 BFC 的条件包括:常见的用途包括: 写过的动画效果overflow有哪些属性visible&#x…...

.NETCORE中关于swagger的分组
有些时候我们的项目接口过多,就希望对应的swagger能够执行分组,网络上的几乎是千篇一律的分组方法,会累死! 这里提供一个更加高效的分组方法,比如你可以说哪些模块分到哪个组,哪些权限分到哪个组ÿ…...

4.1011
目录 四次挥手中收到乱序的FIN包会如何处理? 在 TIME_WAIT 状态的 TCP 连接,收到 SYN 后会发生什么? 四次挥手中收到乱序的FIN包会如何处理? 如果FIN报文比数据包先道道客户端,此时FIN是一个乱序报文,此时…...

uniapp中引入axios的错误?
场景 在unaipp中使用axios npm i axios 下载完成后 然后在页面中使用 axios.get(“http://3000/searchS”) 然后报错 Adapter http’ is not available in the build 原因 在 UniApp 中使用 Axios 发送 HTTP 请求时,如果出现错误 “Adapter http’ is not available…...

Discuz!论坛发帖标题字数限制80字符可以修改吗?修改发帖标题字数的方法
Discuz!论坛发帖标题字数限制80字符修改方法 1.数据库修改2.修改JS验证字符数文件3.修改模板中写死的字符限制数4.修改函数验证文件5.修改语言包文件6.更新缓存 Discuz X3.4论坛网站帖子标题字数限制80字符,当我们想使用长标题的时候就得一删再删,实在是…...
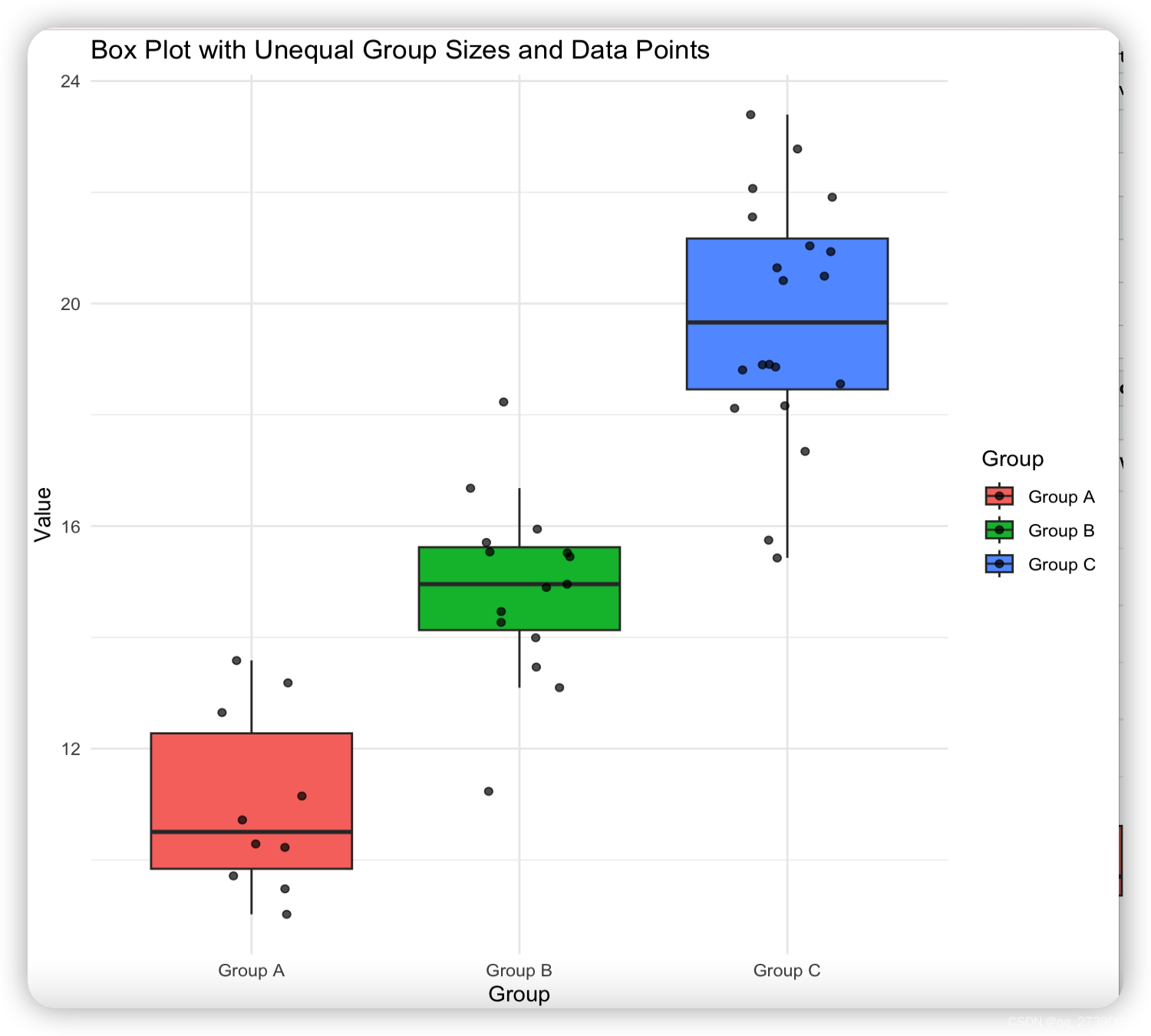
R语言画样本不均衡组的箱线图
# 导入 ggplot2 包 library(ggplot2)# 示例数据框,包含数值数据和分组信息 data <- data.frame(Group c(rep("Group A",10), rep("Group B",15),rep("Group C",20)),Value c(rnorm(10, mean 10, sd 2),rnorm(15, mean 15, sd…...
ArcGIS学习总结(19)——要素转点与空间连接(属性表字段映射)
1.在新创建的面矢量数据的属性表中没有对应的字段信息,为了能够和有属性信息的数据进行匹配,使其具有对应字段的信息。 2.需要匹配的矢量文件属性表信息。 3.对新创建的矢量文件执行要素转点:数据管理工具→要素→要素转点。 4.选择分析工…...

【每日一题Day306】LC228汇总区间 | 双指针
汇总区间【LC228】 给定一个 无重复元素 的 有序 整数数组 nums 。 返回 恰好覆盖数组中所有数字 的 最小有序 区间范围列表 。也就是说,nums 的每个元素都恰好被某个区间范围所覆盖,并且不存在属于某个范围但不属于 nums 的数字 x 。 列表中的每个区间范…...
vue中实现echarts三维散点图
需要安装 echarts 同时引入 echarts-gl 我安装的版本: "echarts": "^5.3.2", "echarts-gl": "^2.0.9", import Vue from "vue"; import * as echarts from "echarts"; Vue.prototype.$echarts echa…...

多头自注意力机制的代码实现
文章目录 1、自注意力机制2、多头注意力机制 transformer的整体结构: 1、自注意力机制 自注意力机制如下: 计算过程: 代码如下: class ScaledDotProductAttention(nn.Module):def __init__(self, embed_dim, key_size, value_…...

抽象工厂模式
目录 了解抽象工厂模式前的前置知识 什么是抽象工厂模式? 为什么要提出抽象工厂模式? 抽象工厂模式中的四大角色? 抽象工厂模式的优缺点? 抽象工厂模式的适用场景? 了解抽象工厂模式前的前置知识 在讲抽象工厂模式…...
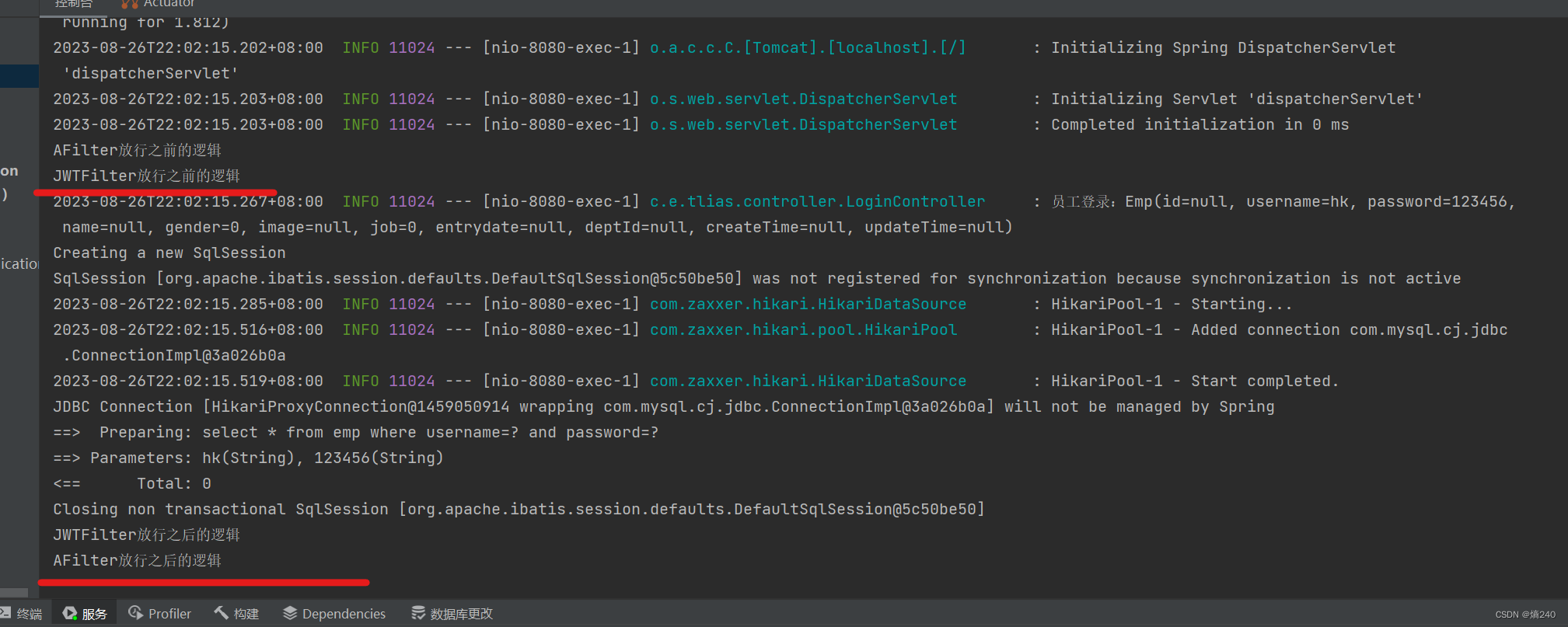
登录校验-Filter-详解
目录 执行流程 拦截路径 过滤器链 小结 执行流程 过滤器Filter拦截到请求之后,首先执行方放行之前的逻辑,然后执行放行操作(doFilter),然后会访问对应的Web资源(对应的Controller类)&#…...

堆栈方法区笔记记录
成员变量分两种: 1)实例变量:没有static修饰,属于对象,存储在堆中,有几个对象就有几份,通过对象点来访问 2)静态变量:由static修饰,属于类,存储在方法区中,只有一份,通过类名点来访…...

新版微信小程序获取用户手机号
小程序手机号验证组件有两种 手机号快速验证组件 //原生写法 <button open-type"getPhoneNumber" bindgetphonenumber"getPhoneNumber"></button>Page({getPhoneNumber (e) {console.log(e.detail.code)} })uniapp写法 <button open-type…...

CSS实践 —— 悬浮盒子阴影加上移效果
悬浮盒子阴影加上移效果 代码 代码 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><title>Title</title><style>body{background-color: #f5f5f5;}.shadow {width: 100px;height: 100px;margin:…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...
