深度强化学习。介绍。深度 Q 网络 (DQN) 算法

马库斯·布赫霍尔茨
一. 引言
深度强化学习的起源是纯粹的强化学习,其中问题通常被框定为马尔可夫决策过程(MDP)。MDP 由一组状态 S 和操作 A 组成。状态之间的转换使用转移概率 P、奖励 R 和贴现因子 gamma 执行。概率转换P(系统动力学)反映了从一个状态到另一个状态的不同转换和奖励发生的次数,其中顺序状态和奖励仅取决于在前一个时间步采取的状态和操作。
强化学习定义了代理执行某些操作(根据策略)以最大化奖励的环境。代理最优行为的基础由贝尔曼方程定义,贝尔曼方程是解决实际优化问题的广泛使用的方法。为了求解贝尔曼最优方程,我们使用动态规划。
当代理存在于环境中并过渡到另一个状态(位置)时,我们需要估计状态 V(s)(位置)的值 — 状态值函数。一旦我们知道每个状态的值,我们就可以弄清楚什么是最好的方法来操作 Q(S, A) — 动作值函数(只需遵循具有最高值的状态)。
这两个映射或函数非常相互关联,可以帮助我们找到
针对我们问题的最佳策略。我们可以表示,状态值函数告诉我们,如果代理遵循策略π,处于状态 S 有多好。
符号的含义如下:
E[X] — 随机变量 X 的期望
π — 政策
Gt — 时间 t 的折扣回报
γ — 贴现率
![]()
但是,操作值函数 q (s, a) 是从状态 S 开始,执行操作 A 并遵循策略π的预期回报,并告诉我们从特定状态执行特定操作有多好,
![]()
值得一提的是,状态值函数和 Q 函数之间的区别在于,值函数指定状态的好坏,而 Q 函数指定状态中动作的好坏。
MDP由贝尔曼方程求解,该方程以美国数学家理查德·贝尔曼的名字命名。该等式有助于找到最佳策略和价值函数。代理根据强加的策略(策略 — 正式地,策略定义为每个可能状态的操作的概率分布)来选择操作。代理可以遵循的不同策略意味着状态的不同值函数。但是,如果目标是最大化收集的奖励,我们必须找到最佳策略,称为最佳策略。
![]()
另一方面,最优状态值函数是与所有其他值函数(最大回报)相比具有更高值的函数,因此最优值函数也可以通过取 Q 的最大值来估计:
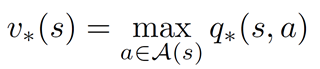
最后,值函数的贝尔曼方程可以表示为:
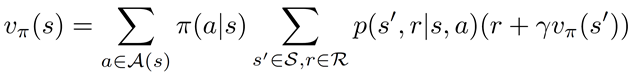
类似地,Q 函数的贝尔曼方程可以表示如下:
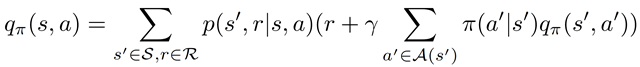
基于最优状态值函数和上述状态值函数动作-值函数方程,我们可以安排最优值函数的最终方程,称为贝尔曼最优方程:
![]()
![]()
通常,强化学习问题是使用 Q — 学习算法来解决的。在这里,如上所述,代理与环境交互并获得奖励。目标是制定最佳政策(行动选择策略)以最大化奖励。在学习过程中,代理更新 Q(S,A) 表(终止在剧集结束时完成 — 达到目标)。
Q — 学习算法按照以下步骤执行:
1. 使用随机值初始化表 Q(S,A)。
2. 对 epsilon 采取行动 (A) — 贪婪的政策并移动到下一个状态 S'
3. 按照更新公式更新先前状态的 Q 值:

最好的开始方法是从OpenAI健身房解决冰冻湖环境。
在冰冻湖环境中(请熟悉OpenAI描述),代理可以停留在16个状态并执行4个不同的操作(在一个状态中)。在本例中,我们的 Q(S,A) 表的大小为 16 x 4。
冰冻湖的代码可以如下:
import gym
import numpy as np
import random
env = gym.make('FrozenLake-v0')'''
While we choose the Action to take, we follow the epsilon-greedy policy: we either explore for new actions with a
probability epsilon or take an action which has a maximum value with a probability 1-epsilon. While updating the Q value,
we simply select the action that has a maximum value + noise
'''def epsilon_greedy_policy(state, epsilon, i):if random.uniform(0,1) < epsilon:return env.action_space.sample()else:return np.argmax(Q[state,:] + np.random.randn(1,env.action_space.n)*epsilon)Q = np.zeros([env.observation_space.n, env.action_space.n])# Definitiion of learning hyperparameters
ALPHA = 0.1
GAMMA = 0.999
NUMBER_EPISODES = 3000
epsilon = 0.015total_REWARDS = []
for i in range(NUMBER_EPISODES):#Reset environment. Get first state.state = env.reset()sum_reward = 0done = Falsej = 0#The Q-Table learning algorithmwhile True:action = epsilon_greedy_policy(state, epsilon, i)#Get new state and reward from environmentstate_next, reward, done, _ = env.step(action)#Q table UPDATEQ[state,action] = Q[state,action] + ALPHA * (reward + GAMMA * np.max(Q[state_next,:]) - Q[state,action])sum_reward += rewardstate = state_nextif done == True:breaktotal_REWARDS.append(sum_reward)print ("--- Q[S,A]-Table ---")
print (Q)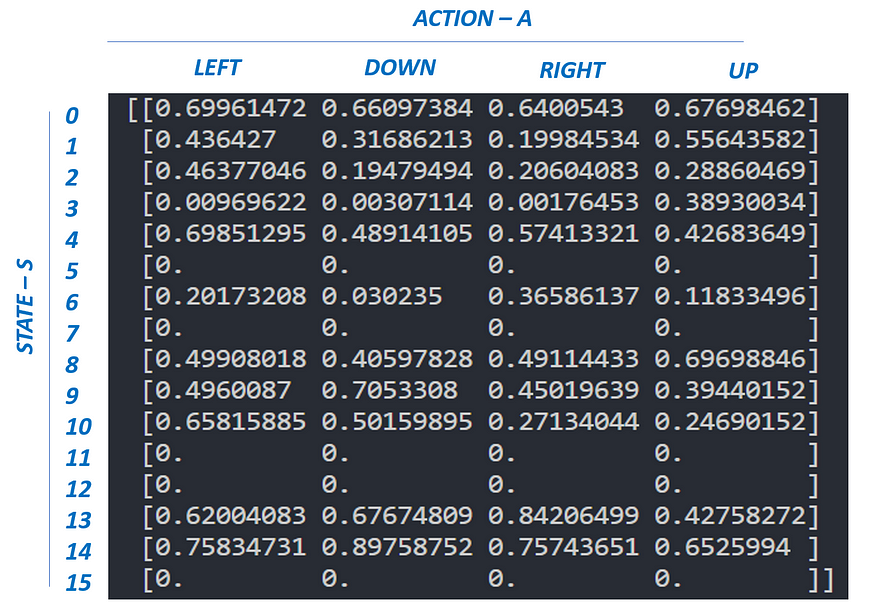
请注意,上面给出的Q -算法属于时间差分学习算法(Richard S. Sutton于1988年)。Q — 算法是一种关闭的 — 策略算法(作为方法学习旧历史数据的能力)。Q — 学习算法的扩展是一种 SARSA(上 — 策略算法。唯一的区别是 Q(S,A) 表更新:
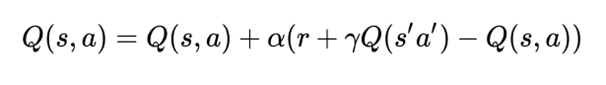
二. 深度强化学习(深度 Q — 网络 — DQN)
强化学习可以充分适用于可以管理(迭代)所有可实现状态并将其存储在标准计算机RAM内存中的环境。然而,在状态数量超过当代计算机容量的环境中(对于雅达利游戏,有12833600状态),标准的强化学习方法不是很适用。此外,在实际环境中,代理必须面对连续状态(非离散)、连续变量和连续控制(动作)问题。
考虑到代理必须操作的环境的复杂性(状态数,连续控制),标准明确定义的强化学习Q - 表被深度神经网络(Q - 网络)取代,深度神经网络(Q - 网络)将(非线性近似)环境状态映射到代理操作。网络架构、网络超参数的选择和学习在训练阶段进行(学习 Q — 网络权重)。
DQN允许代理探索非结构化环境并获得知识,随着时间的推移,这些知识使它们有可能模仿人类行为。
三、 学习算法 DQN
下图(在训练过程中)描述了DQN的主要概念,其中Q — 网络作为非线性近似进行,将两种状态映射到一个动作值中。
在训练过程中,代理与环境交互并接收数据,这些数据在学习 Q — 网络期间使用。代理探索环境以构建转换和操作结果的完整图景。一开始,代理随机决定随着时间的推移变得不足的操作。在探索环境时,代理尝试查看 Q — 网络(近似)以决定如何行动。我们将这种方法(随机行为和根据Q - 网络的组合)称为epsilon - greedy方法(Epsilon - greedy action selection块),它只是意味着使用概率超参数epsilon在随机和Q策略之间切换。
所提出的Q学习算法的核心来源于监督学习。
正如上面提到的,目标是用深度神经网络近似一个复杂的非线性函数 Q(S, A)。
类似地,对于监督学习,在 DQN 中,我们可以将损失函数定义为目标值和预测值之间的平方差,并且我们还将尝试通过更新权重来最小化损失(假设代理通过执行一些操作 a 来执行从一个状态 s 到下一个状态 s 的转换并获得奖励 r)。
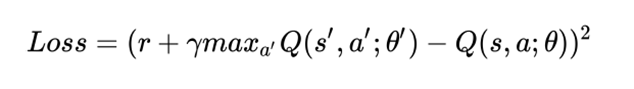
在学习过程中,我们使用两个独立的 Q — 网络(Q_network_local 和 Q_network_target)来计算预测值(权重 θ)和目标值(权重 θ')。目标网络被冻结几个时间步长,然后通过从实际 Q 网络复制权重来更新目标网络权重。将目标 Q — 网络冻结一段时间,然后用实际的 Q 网络权重更新其权重以稳定训练。
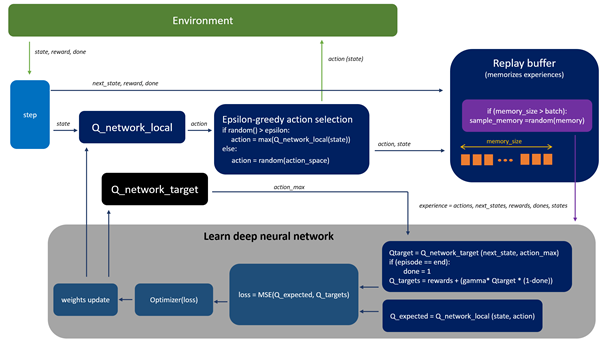
图1.DQN 算法概念
为了使训练过程更加稳定(我们希望避免在相对相关的数据上学习网络,如果我们在连续更新(上次转换)上执行学习,就会发生这种情况),我们应用重放缓冲区来记忆代理行为的体验。然后,对来自重放缓冲区的随机样本进行训练(这降低了代理经验之间的相关性,并帮助代理从广泛的经验中更好地学习)。
DQN 算法可以描述如下:
1. 初始化重播缓冲区,
2. 预处理和环境并将状态 S) 馈送到 DQN,它将返回该状态中所有可能操作的 Q 值。
3. 使用 epsilon 贪婪策略选择一个动作:使用 epsilon 概率,我们选择一个随机动作 A,概率为 1-epsilon。选择具有最大 Q 值的操作,例如 A = argmax(Q(S, A, θ))。
4. 选择操作 A 后,代理在状态 S 中执行所选操作并移动到新状态 S' 并获得奖励 R。
5. 将重播缓冲区中的过渡存储为 <S,A,R,S'>。
6. 接下来,从重放缓冲区中随机采样一些随机批次的转换,并使用公式计算损失:
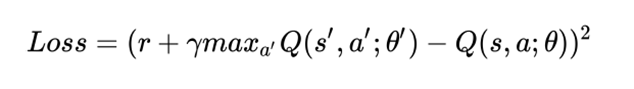
7. 根据实际网络参数执行梯度下降,以最大程度地减少这种损失。
8. 每 k 步后,将我们的实际网络权重复制到目标网络权重。
9. 对 M 集数重复这些步骤。
四、项目设置。结果。
在本节中,我将介绍Udacity(深度强化学习)的项目实施结果 - 请查看我的GitHub。
a. 项目目标
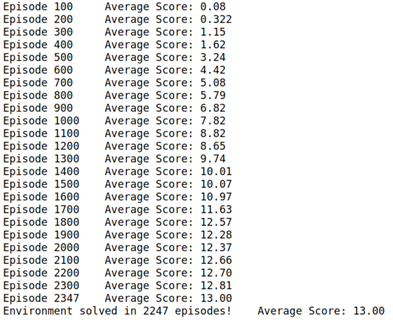
在这个项目中,目标是训练代理在方形环境中导航如何收集黄色香蕉。项目要求是在连续 13 集内收集 +100 的平均分数。
b.在导航项目中,应用了神经网络架构和超参数的以下设置:
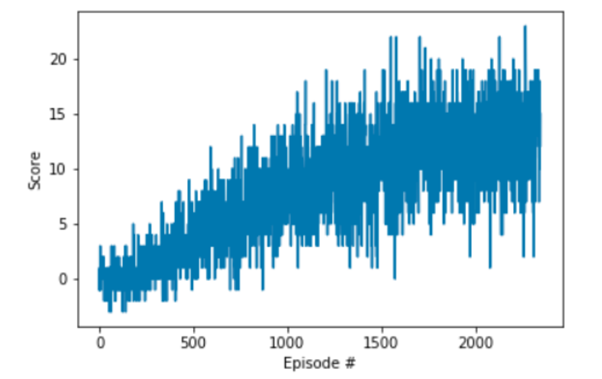
下面描绘的每集奖励图说明了代理在播放 100 集时能够获得至少 +13 的平均奖励(超过 2247 集)。
Q-网络架构:
输入层 FC1:37 个节点输入,64 个节点输出 隐藏层 FC2:64 个节点输入,64 个节点输出 隐藏层 FC3:64 个节点输入,64 个节点输出 输出层:64 个节点输入,4 个输出
— 动作大小
应用的超参数:
BUFFER_SIZE = int(1e5) # 重播缓冲区大小 BATCH_SIZE = 64 # 迷你批量大小
伽玛 = 0.99 # 折扣因子
TAU = 1e-3 # 用于目标参数
的软更新 LR = 5e-4 # 学习率
UPDATE_EVERY = 4 # 更新网络
的频率 厄普西隆开始 = 1.0 厄普西隆开始 = 0.01
厄普西隆衰减 = 0.999
五、未来工作的想法
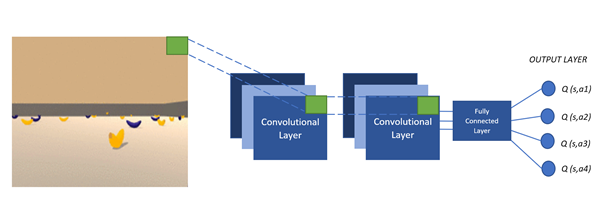
考虑到深度学习的经验,未来的工作将集中在应用图像管理(从像素中学习)。下图显示了 DQN 的体系结构,其中我们馈送游戏屏幕,Q 网络近似于该游戏状态下所有操作的 Q 值。此外,该动作的估计与讨论的DQN算法相同。
其次,未来的工作将侧重于实施DQN的决斗。在这个新架构中,我们指定了新的优势函数,它指定代理执行操作 a 与其他操作相比有多好(优势可以是正数或负数)。
决斗 DQN 的体系结构与上述 DQN 相同,不同之处在于
末端的连接层分为两个流(见下图)。
在具有一定数量的操作空间处于一种状态的环境中,大多数计算的操作不会对状态产生任何影响。此外,还会有许多具有冗余效果的操作。在这种情况下,新的决斗 DQN 将比 DQN 体系结构更精确地估计 Q 值。
一个流计算值函数,另一个流计算优势函数(以确定哪个操作优先于另一个操作)。

最后,我们可以考虑从人类偏好中学习(OpenAI和Deep Mind)。瘦新概念的主要思想是根据人类的反馈来学习代理。接收人类反馈的代理将尝试执行人类喜欢的操作并设置
相应的奖励。人与代理的互动直接有助于克服与设计奖励函数和复杂目标函数相关的挑战。

在我的Github中找到这个项目的完整代码。
相关文章:

深度强化学习。介绍。深度 Q 网络 (DQN) 算法
马库斯布赫霍尔茨 一. 引言 深度强化学习的起源是纯粹的强化学习,其中问题通常被框定为马尔可夫决策过程(MDP)。MDP 由一组状态 S 和操作 A 组成。状态之间的转换使用转移概率 P、奖励 R 和贴现因子 gamma 执行。概率转换P(系统动…...

【C++随笔02】左值和右值
【C随笔02】左值和右值 一、左值和右值1、字面理解——左值、右值2、字面理解的问题3、左值、右值4、左值的特征5、 右值的特征6、x和x是左值还是右值7、复合例子8、通常字面量都是一个右值,除字符串字面量以外: 二、左值引用和右值引用三、左值引用1、常…...
几个nlp的小任务(多选问答)
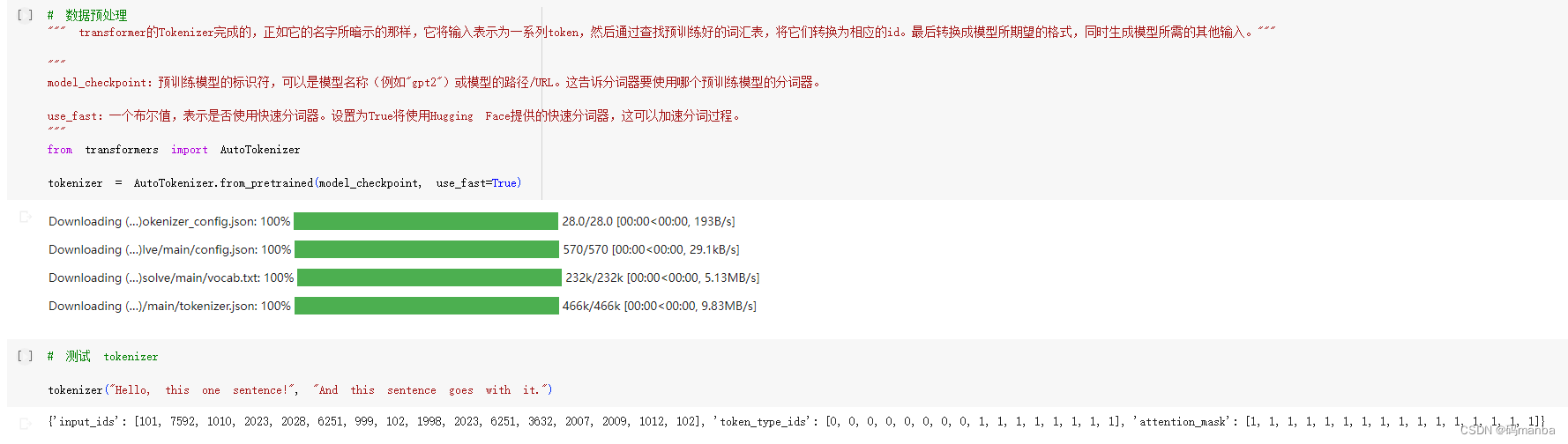
@TOC 安装库 多选问答介绍 定义参数、导入加载函数 缓存数据集 随机选择一些数据展示 进行数据预处理部分(tokenizer) 调用t...

【C++学习记录】为什么需要异常处理,以及Try Catch的使用方法
1.什么是异常,什么是错误? 程序无法保证100%正确运行,万无一失。有的错误在编译时能发现,比如:关键字拼写、变量名未定义、括号不配对、语句末尾缺分号等。这是在编译阶段发现的,称为编译错误。 有的能正常…...

孪生网络(Siamese Network)
基本概念 孪生网络(Siamese Network)是一类神经网络结构,它是由两个或更多个完全相同的网络组成的。孪生网络通常被用于解决基于相似度比较的任务,例如人脸识别、语音识别、目标跟踪等问题。 孪生网络的基本思想是将输入数据同时…...

【Redis】Redis是什么、能干什么、主要功能和工作原理的详细讲解
🚀欢迎来到本文🚀 🍉个人简介:陈童学哦,目前学习C/C、算法、Python、Java等方向,一个正在慢慢前行的普通人。 🏀系列专栏:陈童学的日记 💡其他专栏:CSTL&…...

8月26日,每日信息差
1、上海发布两项支持高级别自动驾驶的5G网络标准,在上海市通管局的指导下,由上海移动和中国信息通信研究院牵头组织二十余家标准起草单位共同参与编写的《支持高级别自动驾驶的5G网络规划建设和验收要求》和《支持高级别自动驾驶的5G网络性能要求》等两项…...
)
云和恩墨面试(部分)
一面 软件架构设计方案应该包含哪些内容,哪些维度 二面 架构师如何保证软件产品质量线程屏障(或者说线程栅栏)是什么,为什么要使用线程屏障事务传播⾏为为NESTED时,当内部事务发生异常时,外部事务会回滚吗?newBing:…...

volatile 关键字详解
目录 volatile volatile 关键用在什么场景下: volatile 关键字防止编译器优化: volatile 是一个在许多编程语言中(包括C和C)用作关键字的标识符。它用于告诉编译器不要对带有该关键字修饰的变量进行优化,以确保变量在…...

Ceph入门到精通-大流量10GB/s LVS+OSPF 高性能架构
LVS 和 LVSkeepalived 这两种架构在平时听得多了,最近才接触到另外一个架构LVSOSPF。这个架构实际上是LVSKeepalived 的升级版本,我们所知道LVSKeepalived 架构是这样子的: 随着业务的扩展,我们可以对web服务器做水平扩展…...

Unity光照相关
1. 光源类型 Unity支持多种类型的光源,包括: 1. 点光源(Point Light):从一个点向四周发射光线,适用于需要突出物体的光源。 2. 平行光(Directional Light):从无限远处…...

Qt基本类型
QT基本数据类型定义在#include <QtGlobal> 中,QT基本数据类型有: 类型名称注释备注qint8signed char有符号8位数据qint16signed short16位数据类型qint32signed short32位有符号数据类型qint64long long int 或(__int64)64位有符号数据类型&#x…...
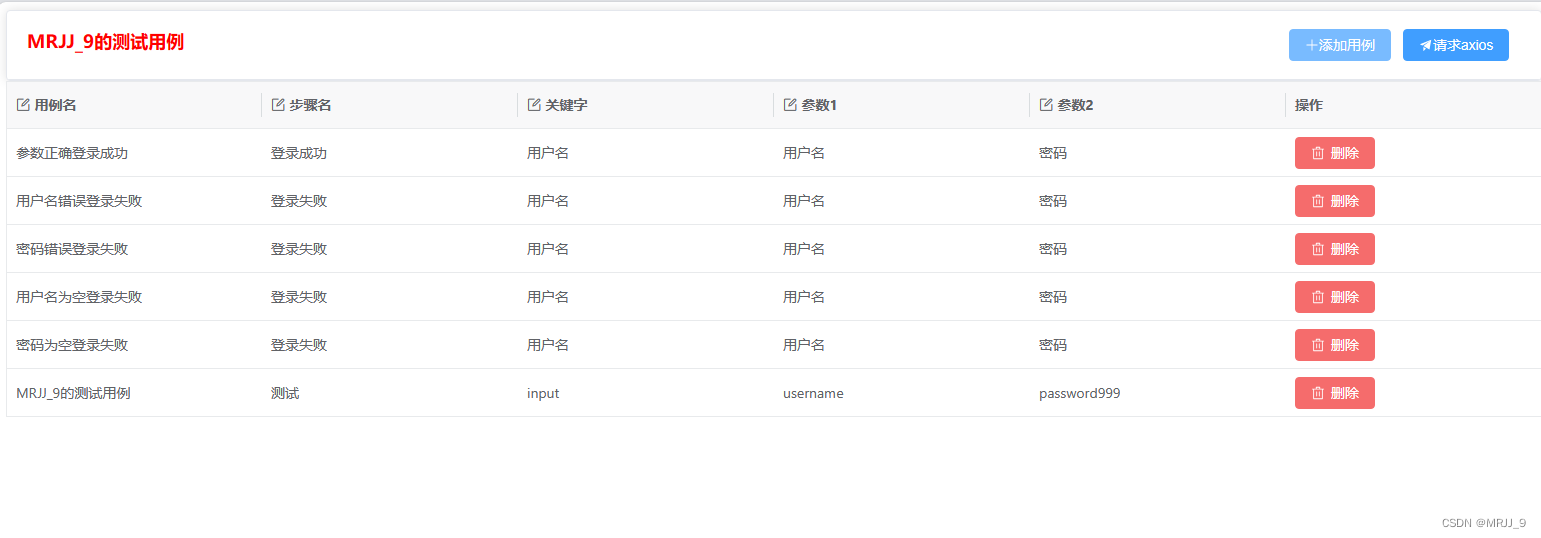
前端基础(Element、vxe-table组件库的使用)
前言:在前端项目中,实际上,会用到组件库里的很多组件,本博客主要介绍Element、vxe-table这两个组件如何使用。 目录 Element 引入element 使用组件的步骤 使用对话框的示例代码 效果展示 vxe-table 引入vxe-table 成果展…...

C++学习记录——이십팔 C++11(4)
文章目录 包装器1、functional2、绑定 这一篇比较简短,只是因为后要写异常和智能指针,所以就把它单独放在了一篇博客,后面新开几篇博客来写异常和智能指针 包装器 1、functional 包装器是一个类模板,对可调用对象类型进行再封装…...
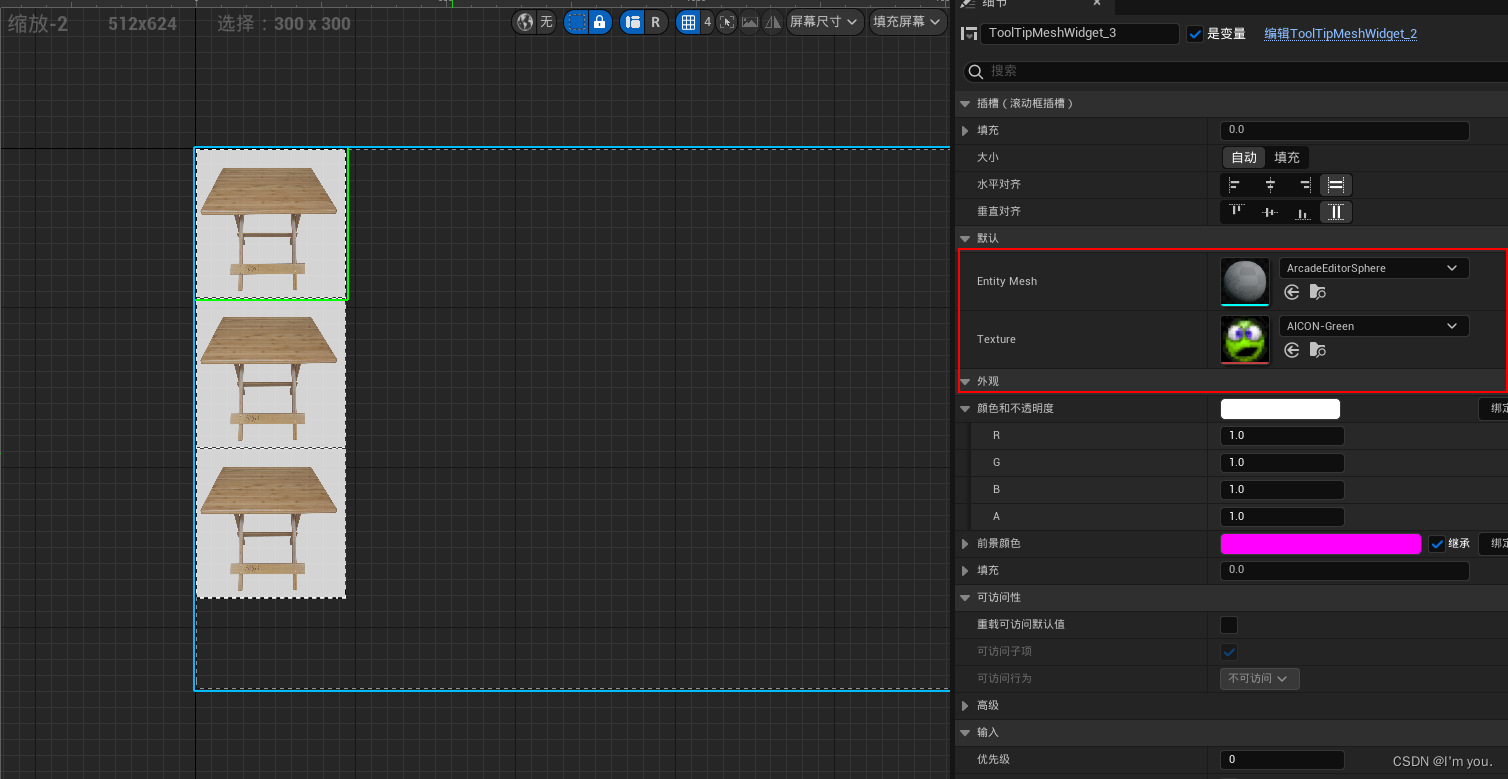
UE学习记录03----UE5.2 使用拖拽生成模型
0.创建蓝图控件,自己想要展示的样子 1.侦测鼠标拖动 2.创建拖动操作 3.拖动结束时生成模型 3.1创建actor , 创建变量EntityMesh设为可编辑 生成Actor,创建变量EntityMesh设为可编辑 屏幕鼠标位置转化为3D场景位置 4.将texture设置为变量并设为可编辑&am…...
)
Spring Cache框架(缓存)
1、介绍: Spring Cache 是一个框架,实现了基于注解的缓存功能,只需要简单加个注解,就能实现缓存功能。它提供了一层抽象,底层可以切换不同的cache实现。具体就是通过CacheManager 接口来实现不同的缓存技术。 针对不同…...
Linux学习之Ubuntu 20使用systemd管理OpenResty服务
sudo cat /etc/issue可以看到操作系统的版本是Ubuntu 20.04.4 LTS,sudo lsb_release -r可以看到版本是20.04,sudo uname -r可以看到内核版本是5.5.19,sudo make -v可以看到版本是GNU Make 4.2.1。 需要先参考我的博客《Linux学习之Ubuntu 2…...

[数据集][目标检测]疲劳驾驶数据集VOC格式4类别-4362张
数据集格式:Pascal VOC格式(不包含分割的txt文件,仅仅包含jpg图片和对应的xml) 图片数量(jpg文件个数):4362 标注数量(xml文件个数):4362 标注类别数:4 标注类别名称:["closed_eye","closed_mouth"…...
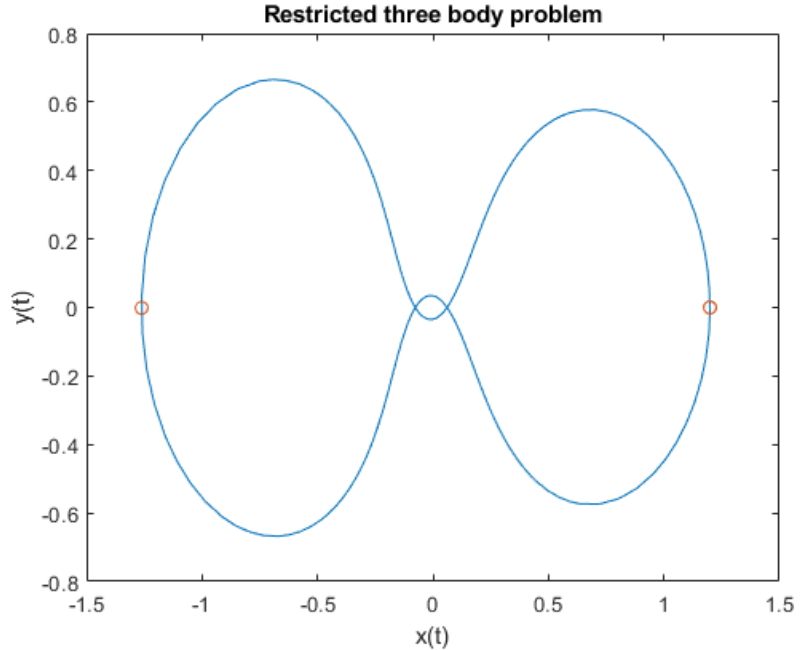
matlab使用教程(25)—常微分方程(ODE)选项
1.ODE 选项摘要 解算 ODE 经常要求微调参数、调整误差容限或向求解器传递附加信息。本主题说明如何指定选项以及每个选项与哪些微分方程求解器兼容。 1.1 选项语法 使用 odeset 函数创建 options 结构体,然后将其作为第四个输入参数传递给求解器。例如࿰…...

MybatisPlus简单到入门
一、MybatisPlus简介 1、入门案例(重点): 1.SpringBoot整合MP1).创建新模块选择,Spring项初始化。2).选择当前模块使用的技术,只保留MySQL Driver就行,不要选择mybatis避免与后面导入mybatisPlus的依赖发…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...

【Linux手册】探秘系统世界:从用户交互到硬件底层的全链路工作之旅
目录 前言 操作系统与驱动程序 是什么,为什么 怎么做 system call 用户操作接口 总结 前言 日常生活中,我们在使用电子设备时,我们所输入执行的每一条指令最终大多都会作用到硬件上,比如下载一款软件最终会下载到硬盘上&am…...

用递归算法解锁「子集」问题 —— LeetCode 78题解析
文章目录 一、题目介绍二、递归思路详解:从决策树开始理解三、解法一:二叉决策树 DFS四、解法二:组合式回溯写法(推荐)五、解法对比 递归算法是编程中一种非常强大且常见的思想,它能够优雅地解决很多复杂的…...

pgsql:还原数据库后出现重复序列导致“more than one owned sequence found“报错问题的解决
问题: pgsql数据库通过备份数据库文件进行还原时,如果表中有自增序列,还原后可能会出现重复的序列,此时若向表中插入新行时会出现“more than one owned sequence found”的报错提示。 点击菜单“其它”-》“序列”,…...
