matlab使用教程(25)—常微分方程(ODE)选项
1.ODE 选项摘要
1.1 选项语法
opts = odeset('RelTol',1e-2,'AbsTol',1e-5);
[t,y] = ode45(@odefun,tspan,y0,opts);if isempty(odeget(opts,'Stats'))
odeset(opts,'Stats','on')
end1.2 选项与每个求解器的兼容性
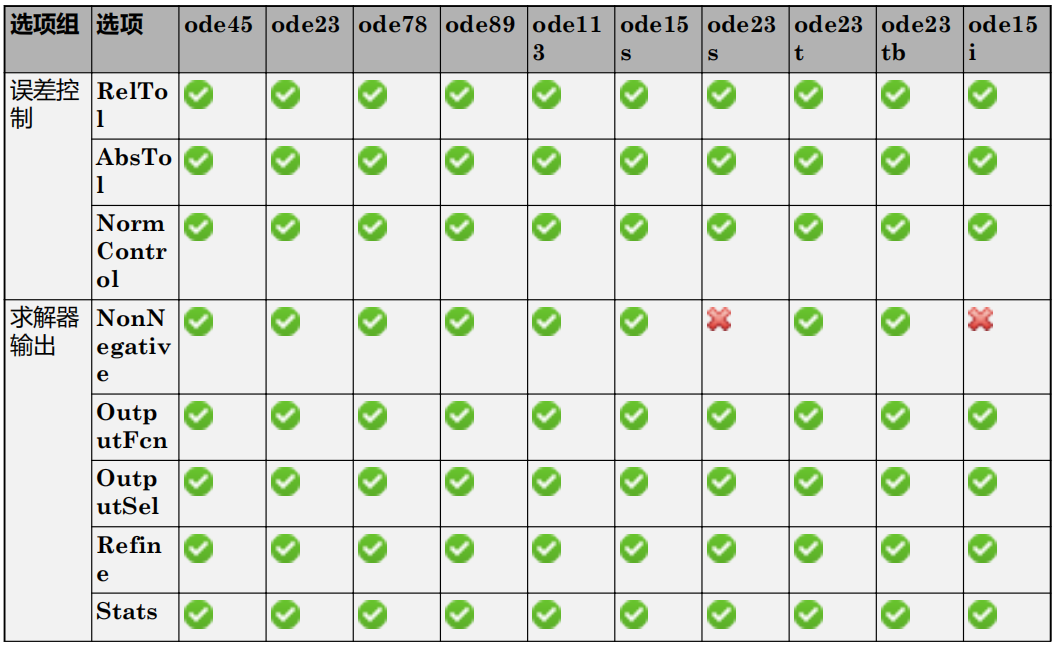

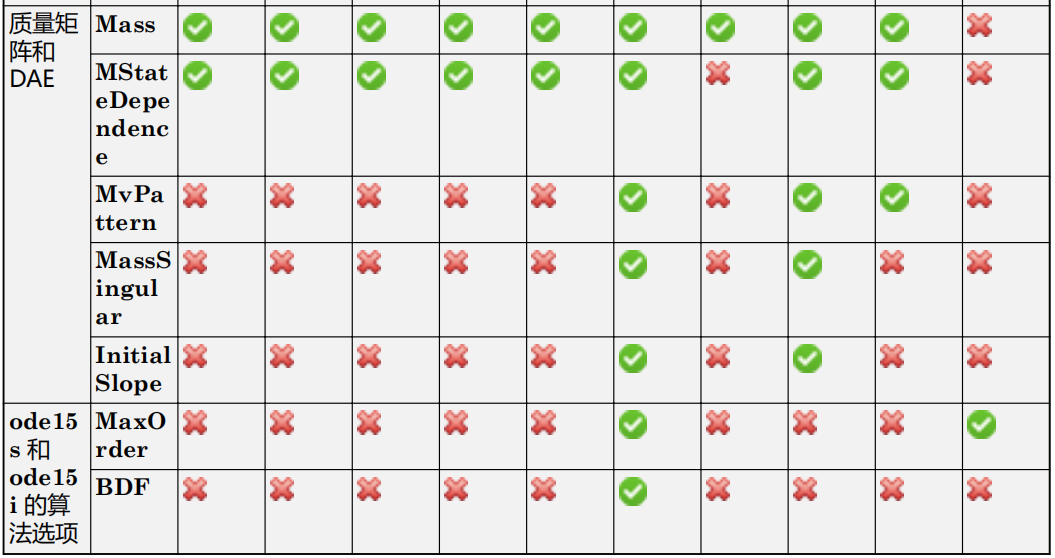
1.3 用法示例
2.ODE 事件位置
2.1 什么是事件位置?
2.2 编写事件函数
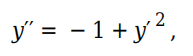
function [position,isterminal,direction] = appleEventsFcn(t,y)
position = y(1); % The value that we want to be zero
isterminal = 1; % Halt integration
direction = 0; % The zero can be approached from either direction
end2.3 事件信息
2.4 局限性
2.5 简单事件位置:弹球

function [value,isterminal,direction] = bounceEvents(t,y)
value = y(1); % Detect height = 0
isterminal = 1; % Stop the integration
direction = -1; % Negative direction onlyballode
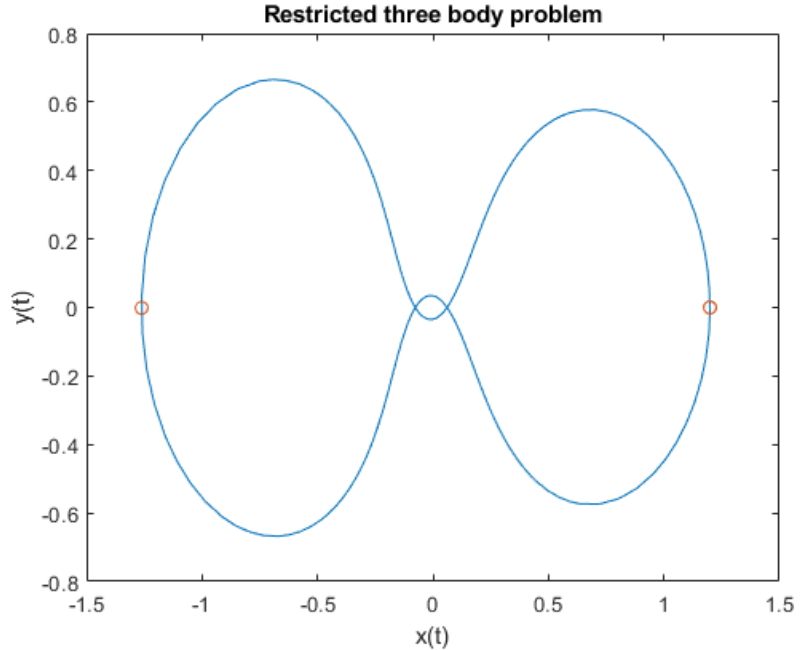
2.6 高级事件位置:限制性三体问题
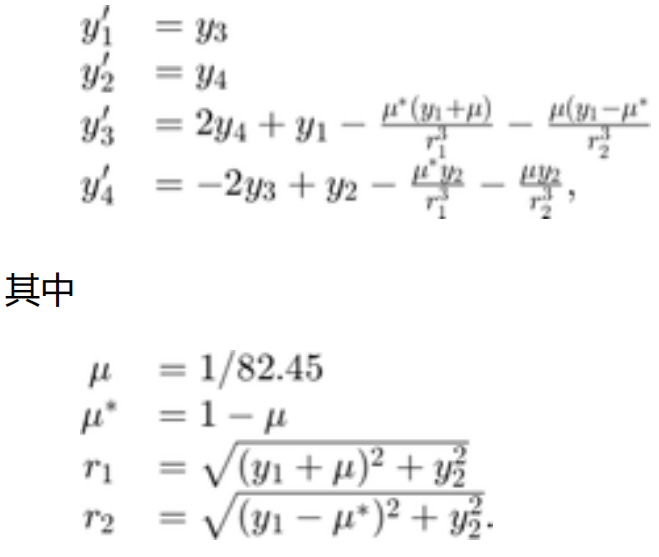
前两个解分量是微小物体的坐标,因此针对一个分量绘制另一个分量可以得到物体的轨迹。orbitode.m 中嵌套的事件函数将搜索两个事件。一个事件查找距离起点最远的点,另一个事件查找宇宙飞船返回到起点的点。即使积分器使用的步长并非通过事件位置确定,也会准确定位事件。在此示例中,指定过零方向的功能非常重要。返回到起点的点和距离起点最远的点具有相同的事件值,并由交叉方向来区分这两个点。为此行为编码的事件函数为
function [value,isterminal,direction] = orbitEvents(t,y)
% dDSQdt is the derivative of the equation for current distance. Local
% minimum/maximum occurs when this value is zero.
dDSQdt = 2 * ((y(1:2)-y0(1:2))' * y(3:4));
value = [dDSQdt; dDSQdt];
isterminal = [1; 0]; % stop at local minimum
direction = [1; -1]; % [local minimum, local maximum]
endorbitode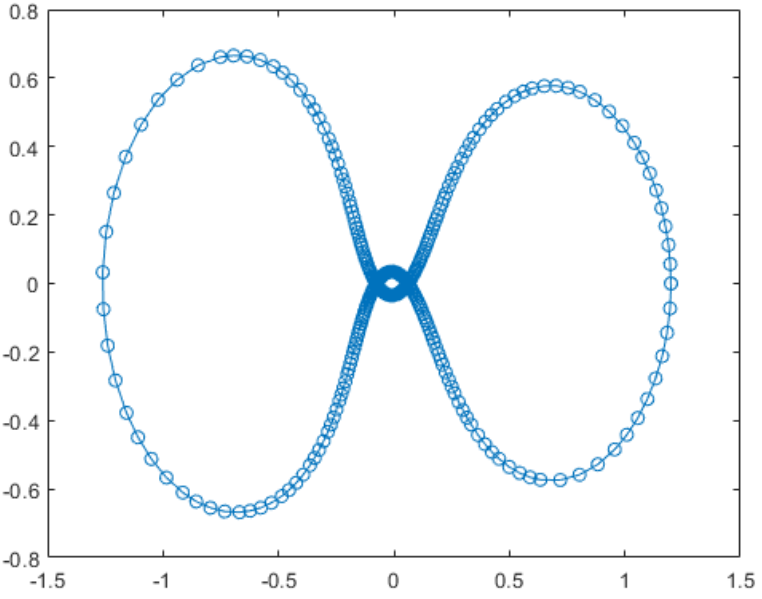
相关文章:

matlab使用教程(25)—常微分方程(ODE)选项
1.ODE 选项摘要 解算 ODE 经常要求微调参数、调整误差容限或向求解器传递附加信息。本主题说明如何指定选项以及每个选项与哪些微分方程求解器兼容。 1.1 选项语法 使用 odeset 函数创建 options 结构体,然后将其作为第四个输入参数传递给求解器。例如࿰…...

MybatisPlus简单到入门
一、MybatisPlus简介 1、入门案例(重点): 1.SpringBoot整合MP1).创建新模块选择,Spring项初始化。2).选择当前模块使用的技术,只保留MySQL Driver就行,不要选择mybatis避免与后面导入mybatisPlus的依赖发…...

9. 优化器
9.1 优化器 ① 损失函数调用backward方法,就可以调用损失函数的反向传播方法,就可以求出我们需要调节的梯度,我们就可以利用我们的优化器就可以根据梯度对参数进行调整,达到整体误差降低的目的。 ② 梯度要清零,如果梯…...

go学习之流程控制语句
文章目录 流程控制语句1.顺序控制2.分支控制2.1单分支2.2双分支单分支和双分支的四个题目switch分支结构 3.循环控制for循环控制while 和do...while的实现 4.跳转控制语句breakcontinuegotoreturngotoreturn 流程控制语句 介绍:在程序中,程序运行的流程…...

docker基于已有容器和通过Dockerfile进行制作镜像配置介绍
目录 一.制作镜像的两种方式 1.在已有容器中更新并提交这个镜像 2.使用Dockerfile来制作 二.基于容器制作镜像 1.格式 (1)主要格式 (2)可选参数 2.案例 基于容器创建镜像设置标签并进行验证是否可用 (1&…...

2022年09月 C/C++(四级)真题解析#中国电子学会#全国青少年软件编程等级考试
第1题:最长上升子序列 一个数的序列bi,当b1 < b2 < … < bS的时候,我们称这个序列是上升的。对于给定的一个序列(a1, a2, …, aN),我们可以得到一些上升的子序列(ai1, ai2, …, aiK),这里1 < i1 < i2 &…...
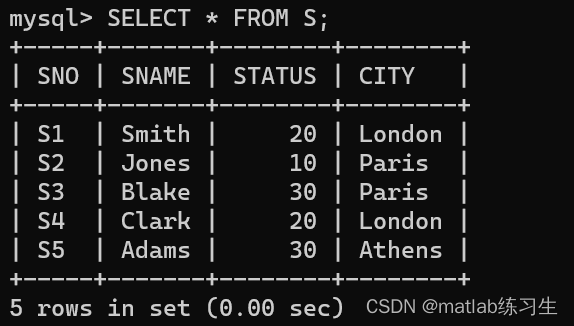
二级MySQL(九)——表格数据处理练习
在Mysql中,可以用INSERT或【REPLACE】语句,向数据库中已一个已有的表中插入一行或多行记录。 在Mysql中,可以用【DELETE】或【TRUNCATE】语句删除表中的所有记录。 在Mysql中,可以用【UPDATE】语句来修改数据表中的记录。 为了完…...

QT ListQvector at赋值出错以及解决办法 QT基础入门【QT存储结构】
1、问题 error: passing const QString as this argument discards qualifiers error: assignment of read-only location vec.QVector<int>::at(0) 在Qt中QList,Qvector一般获取元素都是通过at(index)来获取,但是at()的返回是一个const & 常引用,也就是元素不支…...

STM32 CubeMX (H750)RGB屏幕 LTDC
STM32 CubeMX STM32 RGB888 LTDC STM32 CubeMX一、STM32 CubeMX 设置时钟树LTDC使能设置屏幕参数修改RGB888的GPIO 二、代码部分效果 RGB屏幕线束定义: 一、STM32 CubeMX 设置 时钟树 这里设置的时钟,关于刷新速度 举例子:LCD_CLK24MHz 时…...

Redis问题集合(三)在Redis容器里设置键值对
前言 前提是已经拉取了Redis镜像并创建了对应的容器做个记录,方便后续查看 步骤 查看Redis容器的ID:docker ps -a 进入容器:docker exec -it 容器ID /bin/bash进入redis命令行:redis-cli输入密码:auth 配置密码 查看…...
spark中排查Premature EOF: no length prefix available
报错信息 /07/22 10:20:28 WARN DFSClient: Error Recovery for block BP-888461729-172.16.34.148-1397820377004:blk_15089246483_16183344527 in pipeline 172.16.34.64:50010, 172.16.34.223:50010: bad datanode 172.16.34.64:50010 [DataStreamer for file /bdp/data/u9…...

numpy高级函数之where和extract函数
1 numpy.where() 函数返回输入数组中满足给定条件的元素的索引 ---------------------------------------------------- 代码: n1np.random.randint(10,20,10) n2np.where(n1>15) 结果: [17 15 19 15 12 10 16 11 15 13] #原始数组 (array([…...

用Python写一个武侠游戏
前言 在本教程中,我们将使用Python写一个武侠类的游戏,大的框架全部搭好了,很多元素都可以自己添加,让游戏更丰富 📝个人主页→数据挖掘博主ZTLJQ的主页 个人推荐python学习系列: ☄️爬虫JS逆向系列专栏 -…...

Java --- 异常处理
目录 一、什么是异常 二、异常抛出机制 三、如何对待异常 四、 Java异常体系 4.1、Throwable 4.2、Error 4.2、Exception 4.2.1、编译时异常 4.2.2、运行时期异常 五、异常处理 5.1、捕获异常(try-catch) 5.1.2、catch中异常处理方式 …...
CDN/DCDN(全站加速)排查过程中如何获取Eagle ID/UUID
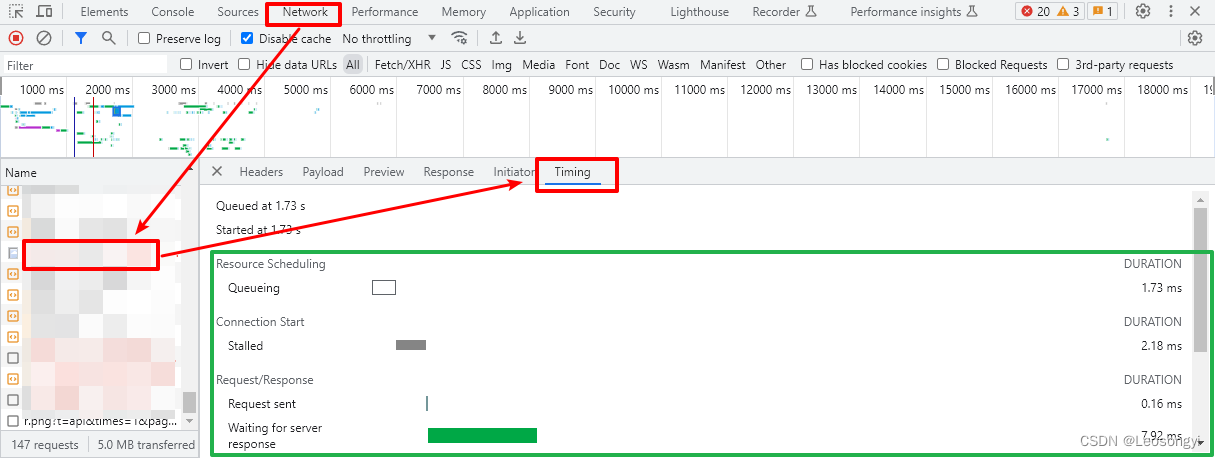
目录 前言1.通过浏览器直接访问文件时获取Request ID 前言 阿里云CDN/DCDN(全站加速)为接收到的每个请求分配唯一的服务器请求ID,作为关联各类日志信息的标识符。当您在使用CDN/DCDN(全站加速)过程中遇到错误且希望阿里云技术支持提供协助时,需要提交失…...

网络安全应急响应预案培训与演练目的
1、增强网络安全意识 网络安全事故隐患往往“生成”于无形。例如,漏洞或黑客攻 击发生之时,受害方企事业单位可能处于非常危险的境地而无所察 觉,一些内部部门人员的网络安全意识也容易懈怠。但不论是内部 员工的疏忽还是管理上的大意&am…...

2023年高教社杯 国赛数学建模思路 - 复盘:校园消费行为分析
文章目录 0 赛题思路1 赛题背景2 分析目标3 数据说明4 数据预处理5 数据分析5.1 食堂就餐行为分析5.2 学生消费行为分析 建模资料 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 赛题背景 校园一卡通是集…...

7.Oracle视图创建与使用
1、视图的创建与使用 在所有进行的SQL语句之中,查询是最复杂的操作,而且查询还和具体的开发要求有关,那么在开发过程之中,程序员完成的并不是是和数据库的所有内容,而更多的是应该考虑到程序的设计结构。可以没有一个项…...

rust学习-不安全操作
在 Rust 中,不安全代码块用于避开编译器的保护策略 四种不安全操作 解引用裸指针通过 FFI (Foreign Function Interface,外部语言函数接口)调用函数调用不安全的函数内联汇编(inline assembly)解引用裸指针 原始指针(raw pointer,裸指针)* 和引用 &T 有类似的功…...
RHCE——八、DNS域名解析服务器
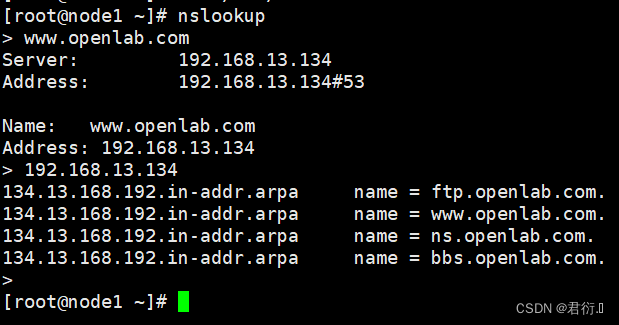
RHCE 一、概述1、产生原因2、作用3、连接方式4、因特网的域名结构4.1 拓扑4.2 分类4.3 域名服务器类型划分 二、DNS域名解析过程1、分类2、解析图:2.1 图:2.2 过程分析 三、搭建DNS域名解析服务器1、概述2、安装软件3、/bind服务中三个关键文件4、配置文…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...

AD学习(3)
1 PCB封装元素组成及简单的PCB封装创建 封装的组成部分: (1)PCB焊盘:表层的铜 ,top层的铜 (2)管脚序号:用来关联原理图中的管脚的序号,原理图的序号需要和PCB封装一一…...

对象回调初步研究
_OBJECT_TYPE结构分析 在介绍什么是对象回调前,首先要熟悉下结构 以我们上篇线程回调介绍过的导出的PsProcessType 结构为例,用_OBJECT_TYPE这个结构来解析它,0x80处就是今天要介绍的回调链表,但是先不着急,先把目光…...

高分辨率图像合成归一化流扩展
大家读完觉得有帮助记得关注和点赞!!! 1 摘要 我们提出了STARFlow,一种基于归一化流的可扩展生成模型,它在高分辨率图像合成方面取得了强大的性能。STARFlow的主要构建块是Transformer自回归流(TARFlow&am…...

Java并发编程实战 Day 11:并发设计模式
【Java并发编程实战 Day 11】并发设计模式 开篇 这是"Java并发编程实战"系列的第11天,今天我们聚焦于并发设计模式。并发设计模式是解决多线程环境下常见问题的经典解决方案,它们不仅提供了优雅的设计思路,还能显著提升系统的性能…...

FOPLP vs CoWoS
以下是 FOPLP(Fan-out panel-level packaging 扇出型面板级封装)与 CoWoS(Chip on Wafer on Substrate)两种先进封装技术的详细对比分析,涵盖技术原理、性能、成本、应用场景及市场趋势等维度: 一、技术原…...
