C语言二——C语言编写一段代码,求一元二次方程的根
这段代码实现了解一元二次方程的根的计算。用户需要输入方程的系数a、b、c,然后根据判别式的值确定方程的根的情况,并进行相应的输出。
- 如果判别式大于0,说明方程有两个实根,分别计算并输出。
- 如果判别式等于0,说明方程有一个重根,计算并输出。
- 如果判别式小于0,说明方程无实根,计算并输出虚根的实部和虚部。
其中,判别式的计算基于数学库中的pow函数和sqrt函数,实根和虚根的计算基于实部和虚部的公式。
如果你有关于这段代码的问题,请继续提问。
#include <stdio.h>
#include <math.h>int main() {double a, b, c;double discriminant, x1, x2;printf("请输入一元二次方程的系数(a、b、c):\n");scanf("%lf %lf %lf", &a, &b, &c);discriminant = pow(b,2) - 4 * a * c;if (discriminant > 0) {x1 = (-b + sqrt(discriminant)) / (2 * a);x2 = (-b - sqrt(discriminant)) / (2 * a);printf("方程有两个实根,分别是 %.2lf 和 %.2lf\n", x1, x2);}else if (discriminant == 0) {x1 = x2 = -b / (2 * a);printf("方程有一个实根,为 %.2lf\n", x1);}else {double realPart = -b / (2 * a);double imaginaryPart = sqrt(-discriminant) / (2 * a);printf("方程无实根,虚根为 %.2lf + %.2lfi 和 %.2lf - %.2lfi\n", realPart, imaginaryPart, realPart, imaginaryPart);}return 0;
}
这是一个用于求解一元二次方程的C语言程序。它会根据用户输入的系数,判断方程的根的情况,并输出相应的结果。
下面是程序的具体分块分析:
- 头文件引入和
main()函数的声明
#include <stdio.h>
#include <math.h>int main() {// ...
}
这里引入了两个头文件 stdio.h 和 math.h,stdio.h 用于使用标准输入输出函数,math.h 用于使用数学函数。然后声明了 main() 函数作为程序的入口。
- 变量声明和用户输入
double a, b, c;
double discriminant, x1, x2;printf("请输入一元二次方程的系数(a、b、c):\n");
scanf("%lf %lf %lf", &a, &b, &c);
在这个块中,声明了所需的变量 a、b、c,分别用来表示一元二次方程的系数。还声明了 discriminant、x1、x2,用来计算方程的判别式和根。通过 printf() 函数向用户输出提示信息,要求用户输入方程的系数。然后使用 scanf() 函数接收用户输入的系数。
- 计算判别式和求解根
discriminant = pow(b,2) - 4 * a * c;if (discriminant > 0) {x1 = (-b + sqrt(discriminant)) / (2 * a);x2 = (-b - sqrt(discriminant)) / (2 * a);printf("方程有两个实根,分别是 %.2lf 和 %.2lf\n", x1, x2);
}
else if (discriminant == 0) {x1 = x2 = -b / (2 * a);printf("方程有一个实根,为 %.2lf\n", x1);
}
else {double realPart = -b / (2 * a);double imaginaryPart = sqrt(-discriminant) / (2 * a);printf("方程无实根,虚根为 %.2lf + %.2lfi 和 %.2lf - %.2lfi\n", realPart, imaginaryPart, realPart, imaginaryPart);
}
这个块中,通过数学函数 pow() 计算出方程的判别式 discriminant。然后根据不同的判别式的值,作出相应的判断:
- 判别式大于0时,方程有两个实根,分别计算出这两个实根并输出。
- 判别式等于0时,方程有一个实根,计算出这个实根并输出。
- 判别式小于0时,方程无实根,计算出虚根的实部和虚部并输出。
- 返回并结束程序
return 0;
这个块用于表示程序执行成功,并通过 return 语句返回一个整数值 0,作为程序的退出码。
以上就是这个程序的具体分块分析。如果您还有其他问题,请随时提问。
相关文章:

C语言二——C语言编写一段代码,求一元二次方程的根
这段代码实现了解一元二次方程的根的计算。用户需要输入方程的系数a、b、c,然后根据判别式的值确定方程的根的情况,并进行相应的输出。 如果判别式大于0,说明方程有两个实根,分别计算并输出。如果判别式等于0,说明方程…...
用Idea把SpringBoot项目打包镜像上传至docker
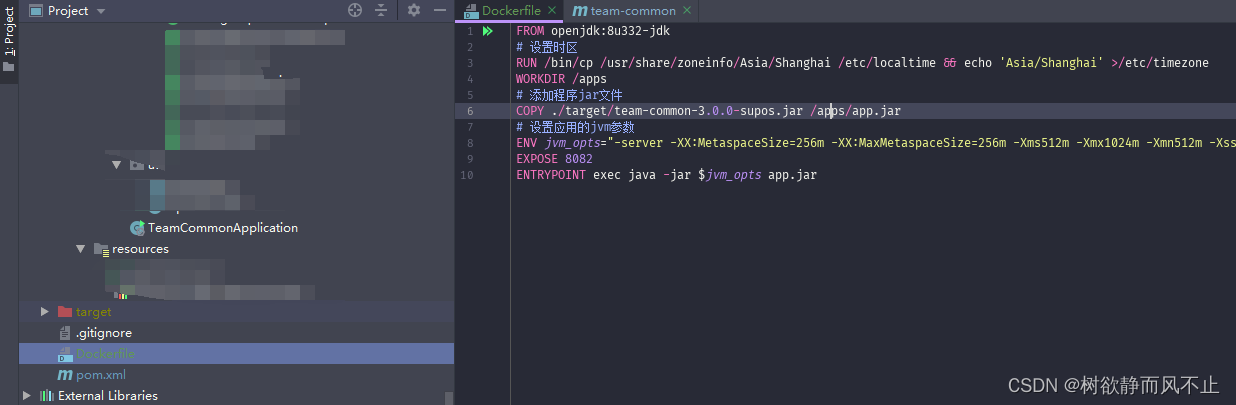
1、设置docker把2375端口开起来 命令查看docker装在哪里 vim docker.service 新增 -H tcp://0.0.0.0:2375 -H unix://var/run/docker.sock 2、配置Dockerfile 我在跟pom同一层 3、配置docker-maven-plugin <plugin><groupId>com.spotify</groupId><arti…...

基于 SVG 的图形交互方案实践
不知道从什么时候起,人们开始喜欢上数字大屏这种“花里胡哨”的东西,仿佛只要用上“科技蓝”这样神奇的色调,就可以让一家公司焕然一新,瞬间变得科技感满满。不管数字大屏的实际意义,是用来帮助企业监控和决策…...

微服务(rpc)
微服务(rpc) 微服务必备的模块生产者消费者管理平台流量控制集群情况下如何做到流量监控 负载均衡服务发现和治理序列化传输序列化和反序列化 微服务是一种架构风格,将一个应用程序拆分为一组小型、独立的服务,每个服务都可以独立…...
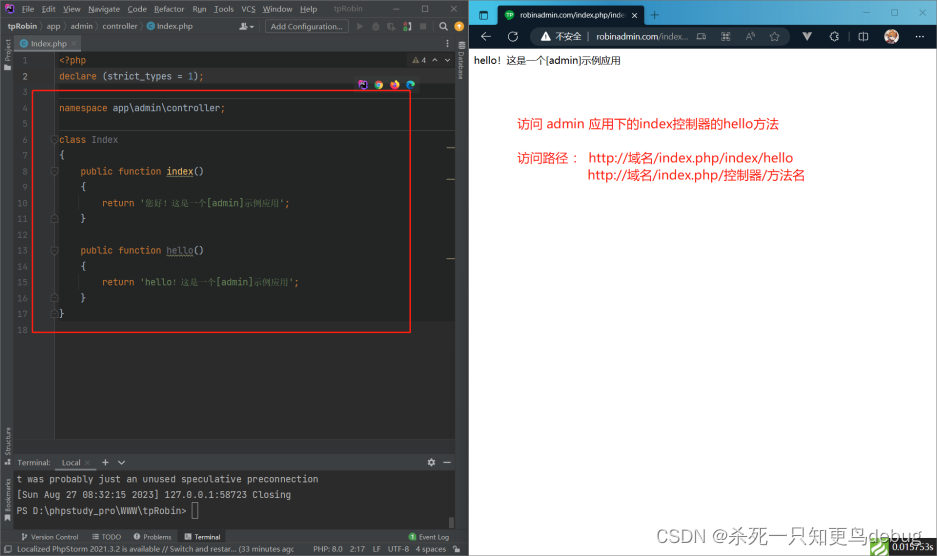
ThinkPHP 多应用配置,及不同域名访问不同应用的配置【详解】
ThinkPHP 多应用配置,及不同域名访问不同应用的配置【详解】 一、安装多应用扩展二、删除项目的中默认的controller文件夹三、创建多应用四、修改config/app.php文件五、测试并且访问多应用六、配置小皮,不同域名访问不同的应用七、小结 一、安装多应用扩…...

Springboot+Mybatis框架是否会取代SSM框架?
个人认真思考的观点:从市场使用来说,会有这个趋势。从技术上来说,不存在被替代这一说。 Spring BootMybatis框架是指使用Spring Boot作为基础框架,并集成Mybatis作为持久层框架的组合,它是一个基于Spring框架的快速开发…...

使用windeployqt和InstallShield打包发布Qt软件的流程
前言 Qt编译之后需要打包发布,并且发布给用户后需要增加一个安装软件,通过安装软件可以实现Qt软件的安装;用于安装软件的软件有很多,这里主要介绍InstallShield使用的流程; 使用windeployqt打包Qt编译后的程序 Qt程序…...
方法阻塞问题)
解决selenium的getdrive()方法阻塞问题
selenium里面的Webdriver的get()方法默认是阻塞的,也就是说要等整个页面全都加载完它才会相应。但我们大部分时候不需要用到页面里的所有东西,也许只需要用到里面的一个元素就行了 所以下面是我的解决方法: 初始化代码: # 设置…...

js的闭包
闭包是有权限访问其他函数作用域的局部变量的一个函数 代码 function outer(){const a1;function f(){console.log(a)}f()}outer() 简单来说:闭包内层函数引用的外层函数变量 为什么要使用闭包? 用此方法可以来统计函数调用次数, 但是如…...
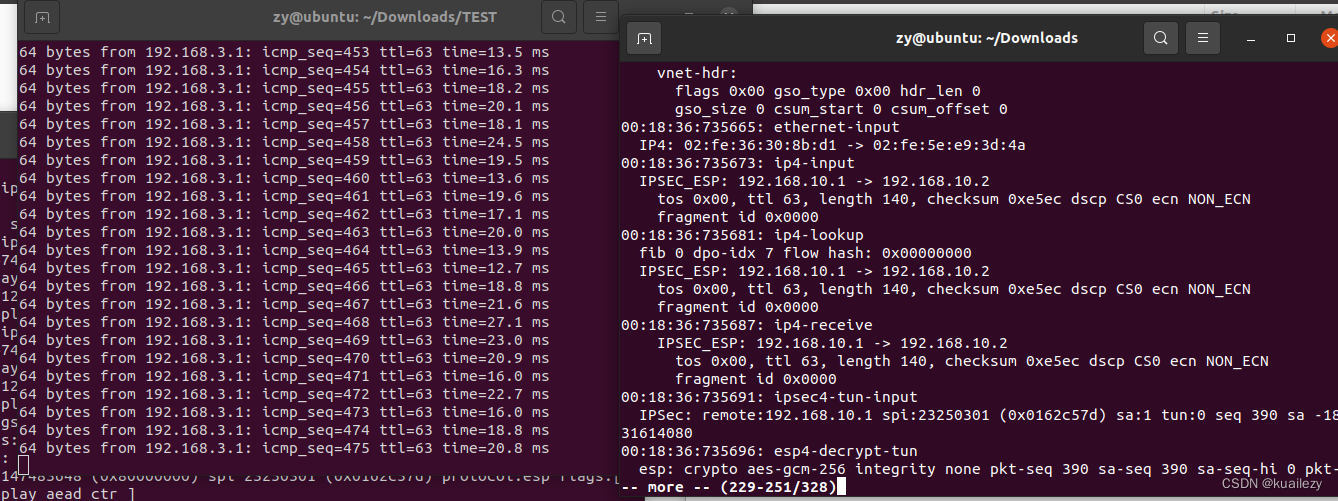
ubuntu20.04 直接安装vpp23.06 测试双 VPP Tunnel Ike2
环境信息:VMware Workstation 17 Pro ubuntu20.04 (清华源) ubuntu 源点进去选:ubuntu-22.04.3-desktop-amd64.iso 如果之前装过VPP,用以下命令确定是否卸载干净: dpkg -l | grep vpp dpkg -l | grep DPDK 卸载: …...

mysql sql 执行流程
监控查询缓存的命中率 show status like ‘%qcache%’; mysql 缓存机制,以及 8.0 为啥取消 select sql_NO_Cache * from 表 where xxx; # 不使用缓存...

go-kafka
go kafka包 本文使用的是kafka-go 6.5k 这个包 其他包参考: 我们在细分市场中非常依赖GO和Kafka。不幸的是,在撰写本文时,Kafka的GO客户库的状态并不理想。可用选项是: 萨拉玛(Sarama) 10k,这…...
如何在windows电脑上安装多个node,并可以进行随意切换
一、进入官网http://nvm.uihtm.com/ 下载 二、启动解压后的程序 1.开始安装nvm 选择要安装的目录 一直下一步–下一步–最后点击完成 3.最后点击完成即可 
《机器学习核心技术》分类算法 - 决策树
「作者主页」:士别三日wyx 「作者简介」:CSDN top100、阿里云博客专家、华为云享专家、网络安全领域优质创作者 「推荐专栏」:小白零基础《Python入门到精通》 决策树 1、决策树API2、决策时实际应用2.1、获取数据集2.2、划分数据集2.3、决策…...
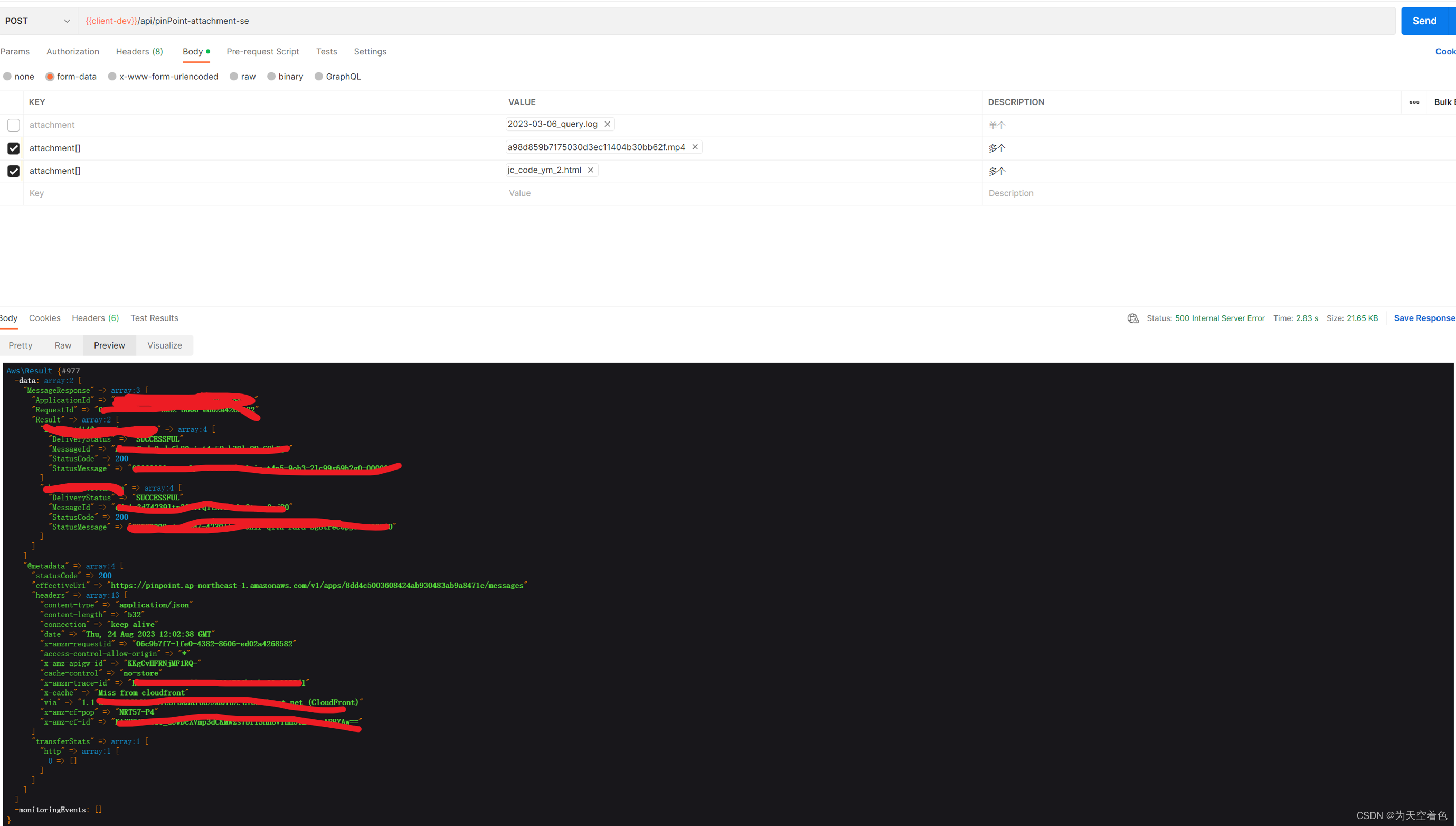
aws PinPoint发附件demo
php 版aws PinPoint发附件demo Laravel8框架,安装了"aws/aws-sdk-php": "^3.257" 主要代码: public function sendRawMail(Request $request) {$file $request->file(attachment);/*echo count($file);dd($file);*/$filenam…...
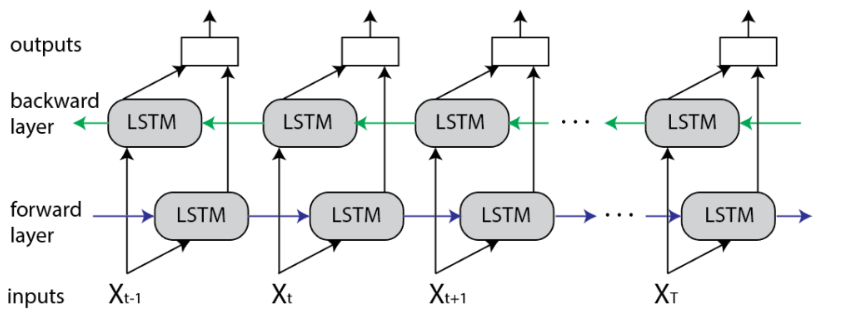
边写代码边学习之Bidirectional LSTM
1. 什么是Bidirectional LSTM 双向 LSTM (BiLSTM) 是一种主要用于自然语言处理的循环神经网络。 与标准 LSTM 不同,输入是双向流动的,并且它能够利用双方的信息。 它也是一个强大的工具,可以在序列的两个方向上对单词和短语之间的顺序依赖…...

Django学习笔记-实现联机对战
笔记内容转载自 AcWing 的 Django 框架课讲义,课程链接:AcWing Django 框架课。 CONTENTS 1. 统一长度单位2. 增加联机对战模式3. 配置Django Channels 1. 统一长度单位 多人模式中每个玩家所看到的地图相对来说应该是一样的,因此需要固定地…...
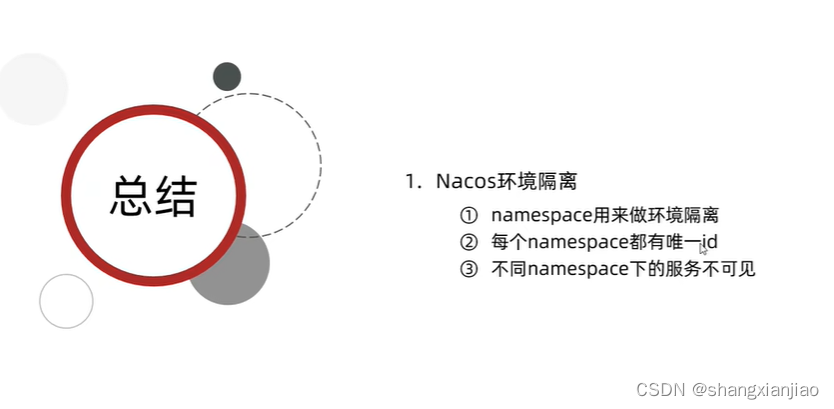
nacos总结1
5.Nacos注册中心 国内公司一般都推崇阿里巴巴的技术,比如注册中心,SpringCloudAlibaba也推出了一个名为Nacos的注册中心。 5.1.认识和安装Nacos Nacos是阿里巴巴的产品,现在是SpringCloud中的一个组件。相比Eureka功能更加丰富,…...
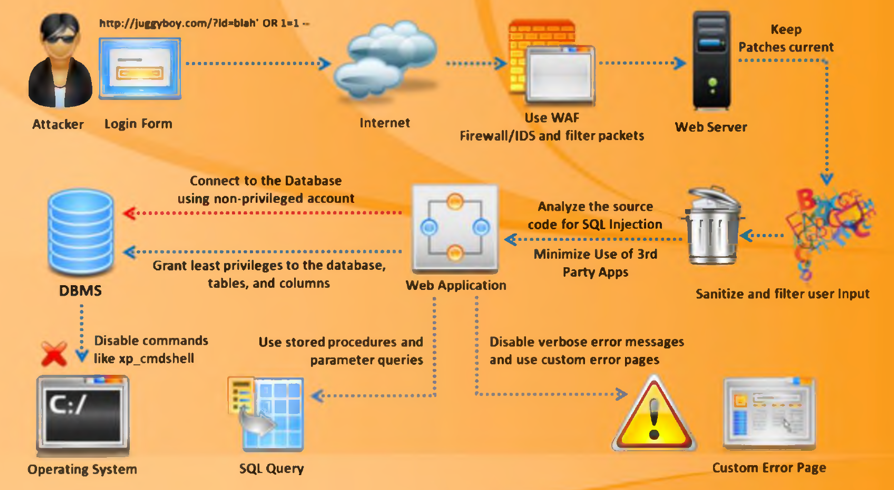
Web安全测试(三):SQL注入漏洞
一、前言 结合内部资料,与安全渗透部门同事合力整理的安全测试相关资料教程,全方位涵盖电商、支付、金融、网络、数据库等领域的安全测试,覆盖Web、APP、中间件、内外网、Linux、Windows多个平台。学完后一定能成为安全大佬! 全部…...
Webstorm 入门级玩转uni-app 项目-微信小程序+移动端项目方案
1. Webstorm uni-app语法插件 : Uniapp Support Uniapp Support - IntelliJ IDEs Plugin | Marketplace 第一个是不收费,第二个收费 我选择了第二个Uniapp Support ,有试用30天,安装重启webstorm之后,可以提高生产率…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...
