微积分基本概念
微分
函数的微分是指对函数的局部变化的一种线性描述。微分可以近似地描述当函数自变量的取值作足够小的改变时,函数的值是怎样改变的。。对于函数 y = f ( x ) y = f(x) y=f(x) 的微分记作:
d y = f ′ ( x ) d x d_y = f^{'}(x)d_x dy=f′(x)dx
微分和导数的区别在于:导数是曲线在那个点的切线斜率,而微分是那个切线的一元线性方程。
微分的几何意义:是用局部切线段近似代替曲线段,即非线性函数局部线性化。
积分
积分可以分为定积分和不定积分两种。
定积分
对于函数 f ( x ) f(x) f(x) 在区间 [a,b] 上定积分记作:
∫ b a f ( x ) d x \int^{a}_{b}f(x)d_x ∫baf(x)dx
其几何意义为函数 f ( x ) f(x) f(x)在区间[a,b]上的覆盖面积,如下图:


不定积分
不定积分是导数的逆运算,即反导数。当 f f f是 F F F的导数时,则 F F F是 f f f的不定积分。常用公式如下:
- ∫ a d x = a x + C \int ad_x = ax + C ∫adx=ax+C
- ∫ x a d x = 1 a + 1 x a + 1 + C \int x^{a}d_x = {1\over a+1}x^{a+1} + C ∫xadx=a+11xa+1+C
- ∫ 1 x = l n ∣ x ∣ + C \int {1 \over x} = ln|x| + C ∫x1=ln∣x∣+C
- ∫ a x d x = a x l n a + C \int {a^xdx} = {a^x\over lna} + C ∫axdx=lnaax+C
- ∫ s i n x d x = − c o s x + C \int sin\ x\ dx = -cos\ x + C ∫sin x dx=−cos x+C
- ∫ c o s x d x = s i n x + C \int cos\ x\ dx = sin\ x + C ∫cos x dx=sin x+C
- ∫ t a n x d x = − l n ∣ c o s x ∣ + C \int tan\ x\ dx = -ln|cos\ x| + C ∫tan x dx=−ln∣cos x∣+C
泰勒公式
用多项式拟合原函数:
f ( x ) = f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) + f ′ ′ ( x 0 ) 2 ! ( x − x 0 ) 2 + . . . + f n ( x 0 ) n ! ( x − x 0 ) n + . . . f(x) = f(x_0) + f^{'}(x_0)(x - x_0) + {f^{''}(x_0) \over 2!}(x - x_0)^2 + ... + {f^{n}(x_0) \over n!}(x - x_0)^n + ... f(x)=f(x0)+f′(x0)(x−x0)+2!f′′(x0)(x−x0)2+...+n!fn(x0)(x−x0)n+...
几何分析
如下内容来自如何通俗地解释泰勒公式?,因为在 x 0 x_0 x0点的任意阶导数都为常数,暂且不管,对于幂函数有如下特点:
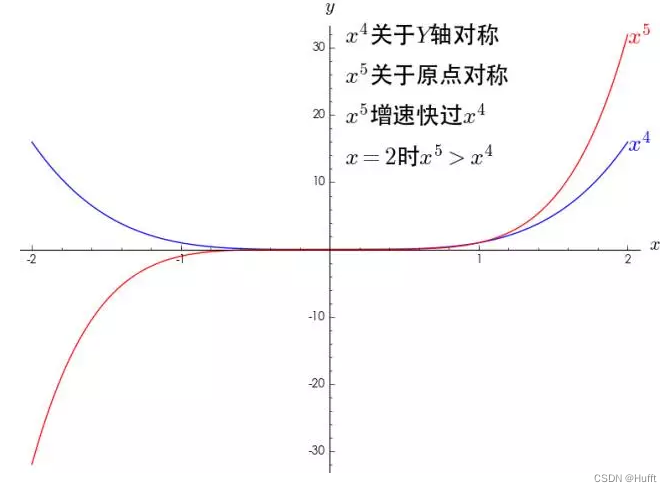
多个幂函数相加:

增加阶乘后效果如下:

通过改变系数,多项式可以像铁丝一样弯成任意的函数曲线,对于 e ( x ) e(x) e(x)拟合:

相关文章:

微积分基本概念
微分 函数的微分是指对函数的局部变化的一种线性描述。微分可以近似地描述当函数自变量的取值作足够小的改变时,函数的值是怎样改变的。。对于函数 y f ( x ) y f(x) yf(x) 的微分记作: d y f ′ ( x ) d x d_y f^{}(x)d_x dyf′(x)dx 微分和…...
【业务功能篇78】微服务-前端后端校验- 统一异常处理-JSR-303-validation注解
5. 前端校验 我们在前端提交的表单数据,我们也是需要对提交的数据做相关的校验的 Form 组件提供了表单验证的功能,只需要通过 rules 属性传入约定的验证规则,并将 Form-Item 的 prop 属性设置为需校验的字段名即可 校验的页面效果 前端数据…...

pytorch的用法
...

Qt 设置窗口背景
窗口背景无非两种:背景色、背景图片。Qt中窗口背景如何设置? 一、QPalette设置背景 二、实现paintEvent,使用QPainter来绘制背景 三、使用QSS来设置背景 关于QSS的使用不想多说,一般我不用QSS设置窗口背景,也不建议…...

大模型是什么?泰迪大模型能够解决企业哪些痛点?
什么是大模型? 大模型是指模型具有庞大的参数规模和复杂程度的机器学习模型。在深度学习领域,大模型通常是指具有数百万到数十亿参数的神经网络模型。这些模型需要大量的计算资源和存储空间来训练和存储,并且往往需要进行分布式计算和特殊…...

YOLOv7-tracker 目标追踪 输入视频帧
目录 1 项目安装1.1 环境搭建1.2 项目下载1.3 权重下载1.4 环境安装1.5 上传待检测的视频帧 2 视频帧检测与追踪2.1 检测与追踪2.3 结果 参考项目:https://github.com/JackWoo0831/Yolov7-tracker/tree/master github链接:https://github.com/Whiffe/Yo…...

C语言二——C语言编写一段代码,求一元二次方程的根
这段代码实现了解一元二次方程的根的计算。用户需要输入方程的系数a、b、c,然后根据判别式的值确定方程的根的情况,并进行相应的输出。 如果判别式大于0,说明方程有两个实根,分别计算并输出。如果判别式等于0,说明方程…...
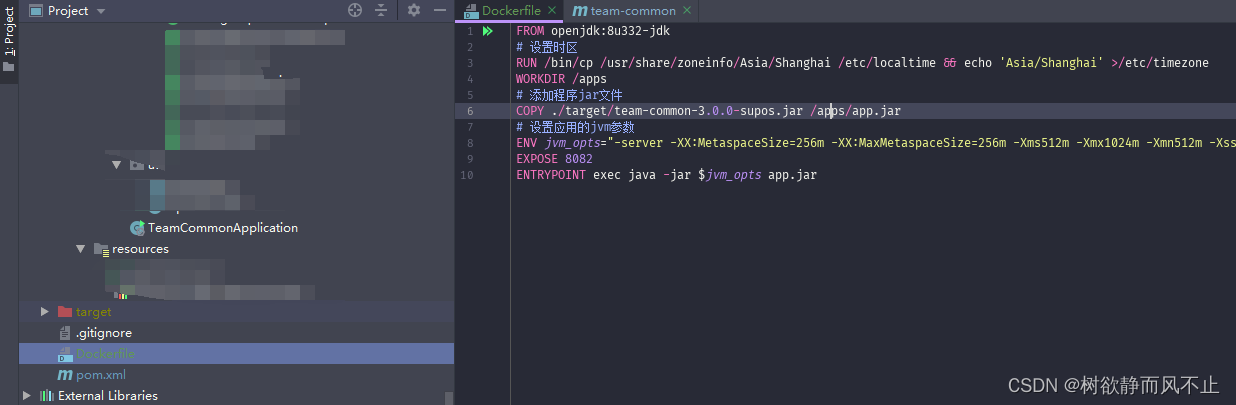
用Idea把SpringBoot项目打包镜像上传至docker
1、设置docker把2375端口开起来 命令查看docker装在哪里 vim docker.service 新增 -H tcp://0.0.0.0:2375 -H unix://var/run/docker.sock 2、配置Dockerfile 我在跟pom同一层 3、配置docker-maven-plugin <plugin><groupId>com.spotify</groupId><arti…...

基于 SVG 的图形交互方案实践
不知道从什么时候起,人们开始喜欢上数字大屏这种“花里胡哨”的东西,仿佛只要用上“科技蓝”这样神奇的色调,就可以让一家公司焕然一新,瞬间变得科技感满满。不管数字大屏的实际意义,是用来帮助企业监控和决策…...

微服务(rpc)
微服务(rpc) 微服务必备的模块生产者消费者管理平台流量控制集群情况下如何做到流量监控 负载均衡服务发现和治理序列化传输序列化和反序列化 微服务是一种架构风格,将一个应用程序拆分为一组小型、独立的服务,每个服务都可以独立…...
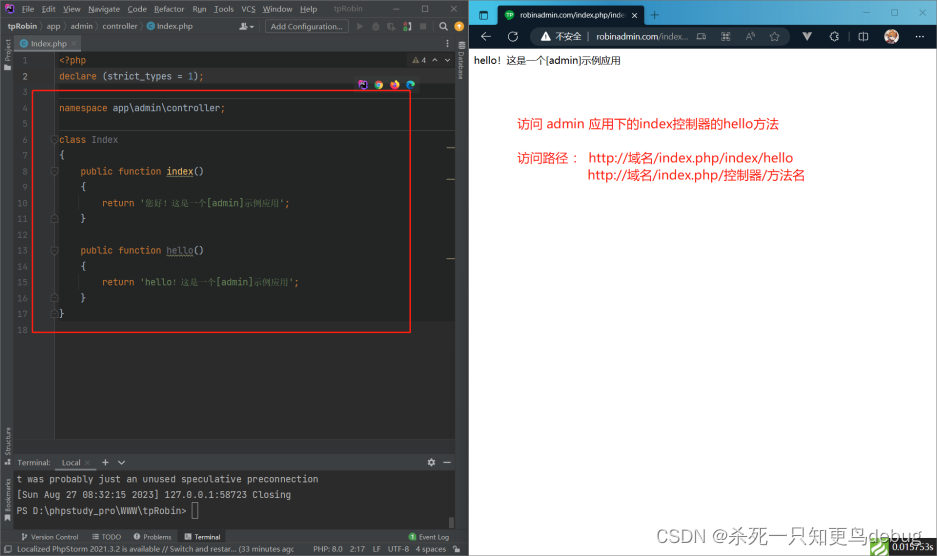
ThinkPHP 多应用配置,及不同域名访问不同应用的配置【详解】
ThinkPHP 多应用配置,及不同域名访问不同应用的配置【详解】 一、安装多应用扩展二、删除项目的中默认的controller文件夹三、创建多应用四、修改config/app.php文件五、测试并且访问多应用六、配置小皮,不同域名访问不同的应用七、小结 一、安装多应用扩…...

Springboot+Mybatis框架是否会取代SSM框架?
个人认真思考的观点:从市场使用来说,会有这个趋势。从技术上来说,不存在被替代这一说。 Spring BootMybatis框架是指使用Spring Boot作为基础框架,并集成Mybatis作为持久层框架的组合,它是一个基于Spring框架的快速开发…...

使用windeployqt和InstallShield打包发布Qt软件的流程
前言 Qt编译之后需要打包发布,并且发布给用户后需要增加一个安装软件,通过安装软件可以实现Qt软件的安装;用于安装软件的软件有很多,这里主要介绍InstallShield使用的流程; 使用windeployqt打包Qt编译后的程序 Qt程序…...
方法阻塞问题)
解决selenium的getdrive()方法阻塞问题
selenium里面的Webdriver的get()方法默认是阻塞的,也就是说要等整个页面全都加载完它才会相应。但我们大部分时候不需要用到页面里的所有东西,也许只需要用到里面的一个元素就行了 所以下面是我的解决方法: 初始化代码: # 设置…...

js的闭包
闭包是有权限访问其他函数作用域的局部变量的一个函数 代码 function outer(){const a1;function f(){console.log(a)}f()}outer() 简单来说:闭包内层函数引用的外层函数变量 为什么要使用闭包? 用此方法可以来统计函数调用次数, 但是如…...
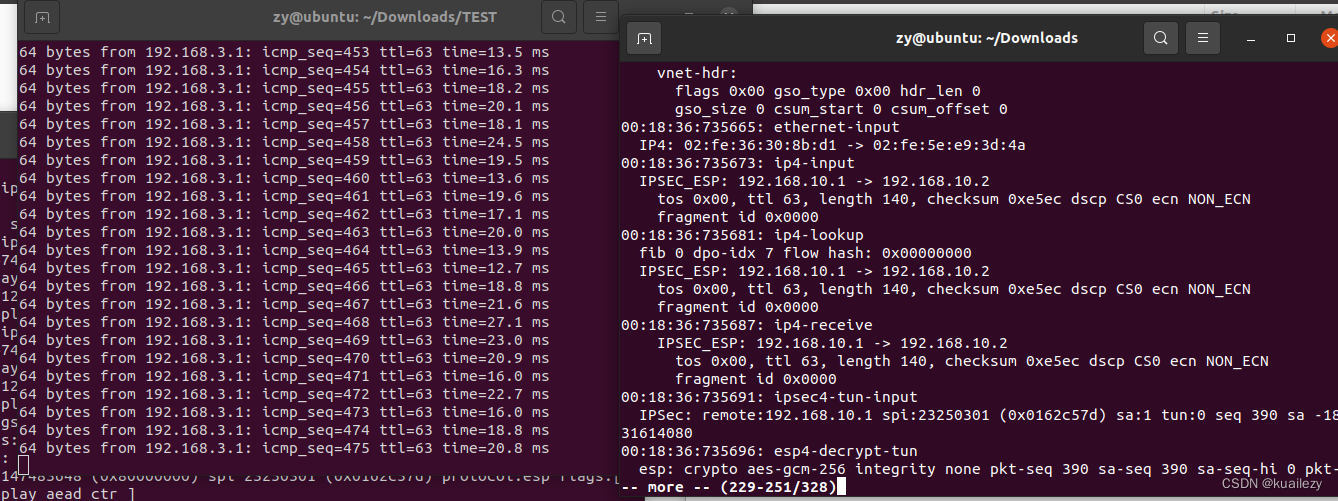
ubuntu20.04 直接安装vpp23.06 测试双 VPP Tunnel Ike2
环境信息:VMware Workstation 17 Pro ubuntu20.04 (清华源) ubuntu 源点进去选:ubuntu-22.04.3-desktop-amd64.iso 如果之前装过VPP,用以下命令确定是否卸载干净: dpkg -l | grep vpp dpkg -l | grep DPDK 卸载: …...

mysql sql 执行流程
监控查询缓存的命中率 show status like ‘%qcache%’; mysql 缓存机制,以及 8.0 为啥取消 select sql_NO_Cache * from 表 where xxx; # 不使用缓存...

go-kafka
go kafka包 本文使用的是kafka-go 6.5k 这个包 其他包参考: 我们在细分市场中非常依赖GO和Kafka。不幸的是,在撰写本文时,Kafka的GO客户库的状态并不理想。可用选项是: 萨拉玛(Sarama) 10k,这…...
如何在windows电脑上安装多个node,并可以进行随意切换
一、进入官网http://nvm.uihtm.com/ 下载 二、启动解压后的程序 1.开始安装nvm 选择要安装的目录 一直下一步–下一步–最后点击完成 3.最后点击完成即可 
《机器学习核心技术》分类算法 - 决策树
「作者主页」:士别三日wyx 「作者简介」:CSDN top100、阿里云博客专家、华为云享专家、网络安全领域优质创作者 「推荐专栏」:小白零基础《Python入门到精通》 决策树 1、决策树API2、决策时实际应用2.1、获取数据集2.2、划分数据集2.3、决策…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...
