Selenium 遇见伪元素该如何处理?
问题发生
在很多前端页面中,大家会见到很多::before、::after 元素,比如【百度流量研究院】:
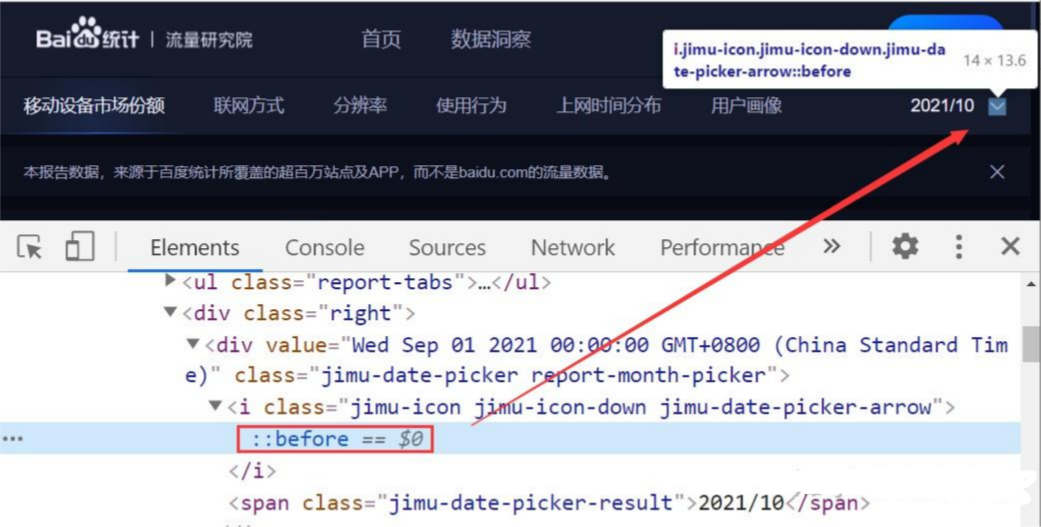
比如【百度疫情大数据平台】:
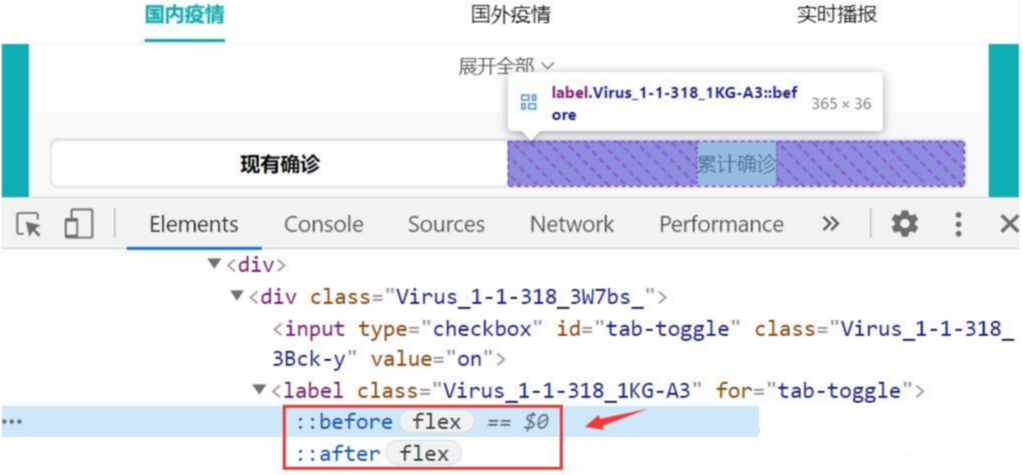
以【百度疫情大数据平台】为例,“累计确诊”文本并没有显示在 HTML 源代码中,如果通过常规的 xpath 元素定位方式是没办法的,因为“累计确诊”文本并不存在当前页面 dom 树中。
如何处理?
我们要弄清楚的是该元素的特殊之处,文本究竟存放在哪?
其实很简单,通过 Chrome 的 F12,我们将 style 选项展示出来:

可以看到元素的文本保存在 CSS 样式里面,通过 content 属性进行设置。
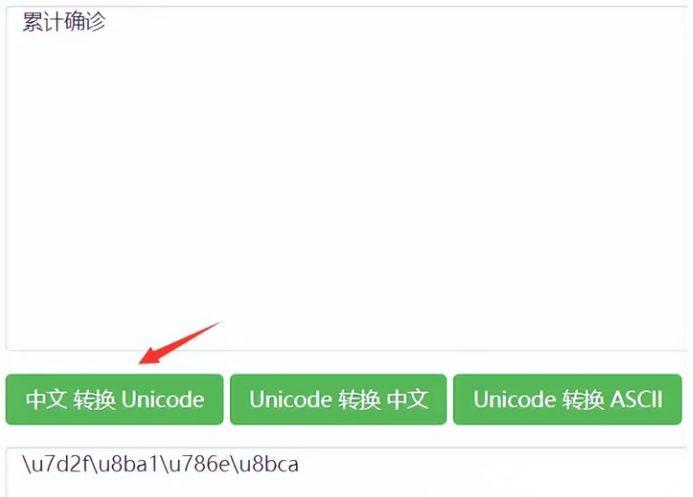
这里还有个小问题:文本根本对不上呢?
因为这里使用了 Unicode 编码,使用在线的 Unicode 编码转换工具即可看到
::after 元素也是同理,这种性质的元素我们称之为伪元素:
之所以被称为伪元素,是因为他们不是真正的页面元素,HTML 没有对应的元素,但是其所有用法和表现行为与真正的页面元素一样,可以对其使用诸如页面元素一样的 CSS 样式,表面上看上去貌似是页面的某些元素来展现,实际上是 CSS 样式展现的行为,因此被称为伪元素。
一、伪元素的定位
由于伪元素是通过 CSS 样式展现的行为,所以我们可以通过 CSS 样式选择器来进行定位,以“百度疫情大数据为例”:
1.先定位伪元素的父元素:div.Virus_1-1-318_3W7bs_
2.再定位到伪元素本身:div.Virus_1-1-318_3W7bs_>label

二、伪元素文本的获取
有些情况下我们需要获取到文本信息,其中伪元素的文本主要是通过 content 属性设置,我们可以通过 JavaScript 可以进行提取:

Selenium 中调用 JavaScript:
JavascriptExecutor jsExecutor = (JavascriptExecutor) driver;
jsExecutor.executeScript("window.getComputedStyle(document.querySelector('.Virus_1-1-318_1KG-A3'),'最后感谢每一个认真阅读我文章的人,礼尚往来总是要有的,虽然不是什么很值钱的东西,如果你用得到的话可以直接拿走:
软件测试面试小程序
被百万人刷爆的软件测试题库!!!谁用谁知道!!!全网最全面试刷题小程序,手机就可以刷题,地铁上公交上,卷起来!
涵盖以下这些面试题板块:
1、软件测试基础理论 ,2、web,app,接口功能测试 ,3、网络 ,4、数据库 ,5、linux
6、web,app,接口自动化 ,7、性能测试 ,8、编程基础,9、hr面试题 ,10、开放性测试题,11、安全测试,12、计算机基础

这些资料,对于【软件测试】的朋友来说应该是最全面最完整的备战仓库,这个仓库也陪伴上万个测试工程师们走过最艰难的路程,希望也能帮助到你!
相关文章:

Selenium 遇见伪元素该如何处理?
问题发生 在很多前端页面中,大家会见到很多::before、::after 元素,比如【百度流量研究院】: 比如【百度疫情大数据平台】: 以【百度疫情大数据平台】为例,“累计确诊”文本并没有显示在 HTML 源代码中&am…...

RPA技术介绍与应用价值
一、什么是RPA技术? RPA(Robotic Process Automation)机器人流程自动化,是一种能够模拟人类来执行重复性任务的新型技术。RPA可实现统筹安排、自动化业务处理,并提升业务工作流处理效率。用户只需通过图形方式显示的计算机操作界面对RPA软件进行动态设定即可。借助RPA (R…...

产品经理,需要具备哪些能力和知识
作为产品经理,需要具备以下能力和知识: 产品管理能力:具备全面的产品管理能力,包括产品策划、需求分析、产品规划、产品设计、项目管理、市场调研和竞争分析等。 用户导向思维:能够理解用户需求和期望,以…...

【C++】map和set
map和set 文章目录 map和set关联式容器setset介绍set的函数测试代码 multiset注意事项测试代码 mapmap介绍map的函数测试代码 关联式容器 前面了解过的vector,list,string等容器都是序列式容器,存储的都是元素本身,底层都是线性的…...
crawlab通过docker单节点部署简单爬虫
crawlab 单节点docker安装 此处介绍的是单节点的方式,多节点的情况可以把爬虫上传到一个节点中,之后会同步到其它节点上 version: 3.3 services:master:image: crawlabteam/crawlabcontainer_name: crawlab_masterrestart: alwaysenvironment:CRAWLAB…...

【STM32】中断与NVIC以外部中断为例
前言 在stm32中姑且可以认为,异常就是中断 单片机上电之后,首先执行启动文件,开辟堆栈之后,开始初始化中断向量表。 NVIC NVIC NVIC是嵌套向量中断控制器,控制着整个芯片中断相关的功能,它跟内核紧密耦…...
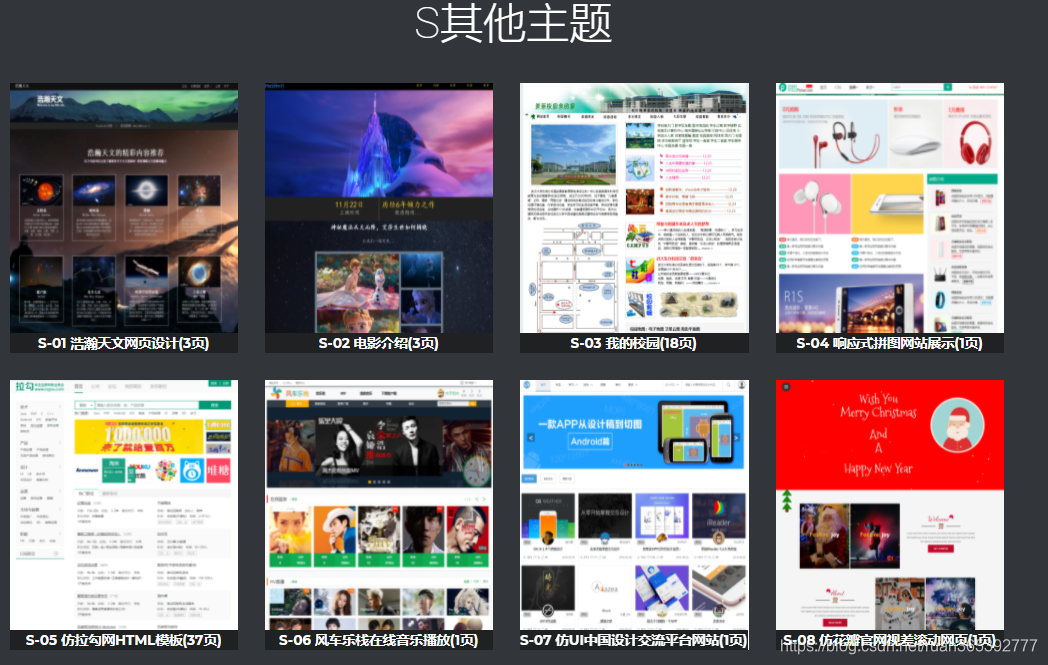
大学生网页设计制作作业实例代码 (全网最全,建议收藏) HTML+CSS+JS
文章目录 📚web前端期末大作业 (1500套) 集合一、网页介绍二、网页集合 三、作品演示A电影主题B漫画主题C商城主题D家乡主题E旅游主题F餐饮/美食主题G环境主题H游戏主题I 个人主题K体育主题L博客主题M汽车主题N文化主题P美妆主题Q企业主题R教育主题S其他主题 &#…...

Llama模型结构解析(源码阅读)
目录 1. LlamaModel整体结构流程图2. LlamaRMSNorm3. LlamaMLP4. LlamaRotaryEmbedding 参考资料: https://zhuanlan.zhihu.com/p/636784644 https://spaces.ac.cn/archives/8265 ——《Transformer升级之路:2、博采众长的旋转式位置编码》 前言&#x…...

基于XML实现SpringIoC配置
目录 SpringIoc创建与使用的大致步骤 一.基于xml配置SpringIoc 二.基于xml配置DI 三.创建IoC容器并获取组件 SpringIoc创建与使用的大致步骤 SpringIoC的创建与使用过程分为3步 1.编写配置信息(编写XML,注解、Java类) 2.创建IoC容器&…...

Kaniko在containerd中无特权快速构建并推送容器镜像
目录 一、kaniko是什么 二、kaniko工作原理 三、kanijo工作在Containerd上 基于serverless的考虑,我们选择了kaniko作为镜像打包工具,它是google提供了一种不需要特权就可以构建的docker镜像构建工具。 一、kaniko是什么 kaniko 是一种在容器或 Kube…...

分享5款不会被打入冷宫的神器软件
检查一下你最近安装的软件,他们是不是都一样无法避免最终被你打入冷宫的命运?我们明明很懂“在精不在多”的道理,却依然让我们的电脑塞满了形形色色无用的软件。你需要知道的是,如何找到一款适合自己且真正实用的电脑软件。 自…...
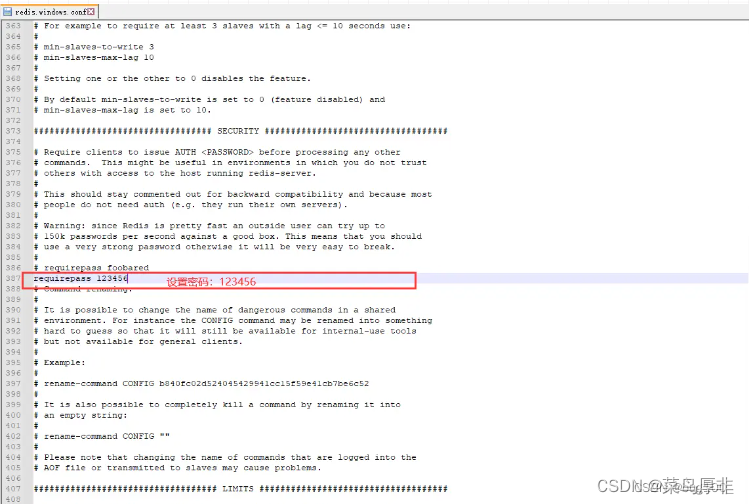
Windows如何部署Redis
一、简介 Redis (Remote Dictionary Server) 是一个由意大利人 Salvatore Sanfilippo 开发的 key-value 存储系统,具有极高的读写性能,读的速度可达 110000 次/s,写的速度可达 81000 次/s 。 二、下载 访问 https://github.com/tporadows…...

VUE数据双向绑定原理解析
VUE数据双向绑定原理解析 在Vue.js中,数据双向绑定是一项非常强大的功能。它使开发者能够轻松地将模板与数据进行动态关联,实现了页面和数据之间的实时同步更新。本文将深入探讨VUE中数据双向绑定的原理,并通过代码示例演示其工作机制。 1.…...

SSM商城项目实战:订单管理
SSM商城项目实战:订单管理 在SSM商城项目中,订单管理是一个非常重要的功能模块。本文将详细介绍订单管理的实现思路和步骤代码。 实现SSM商城项目中订单管理功能的思路如下: 设计数据库表结构:根据订单管理的需求,设计…...
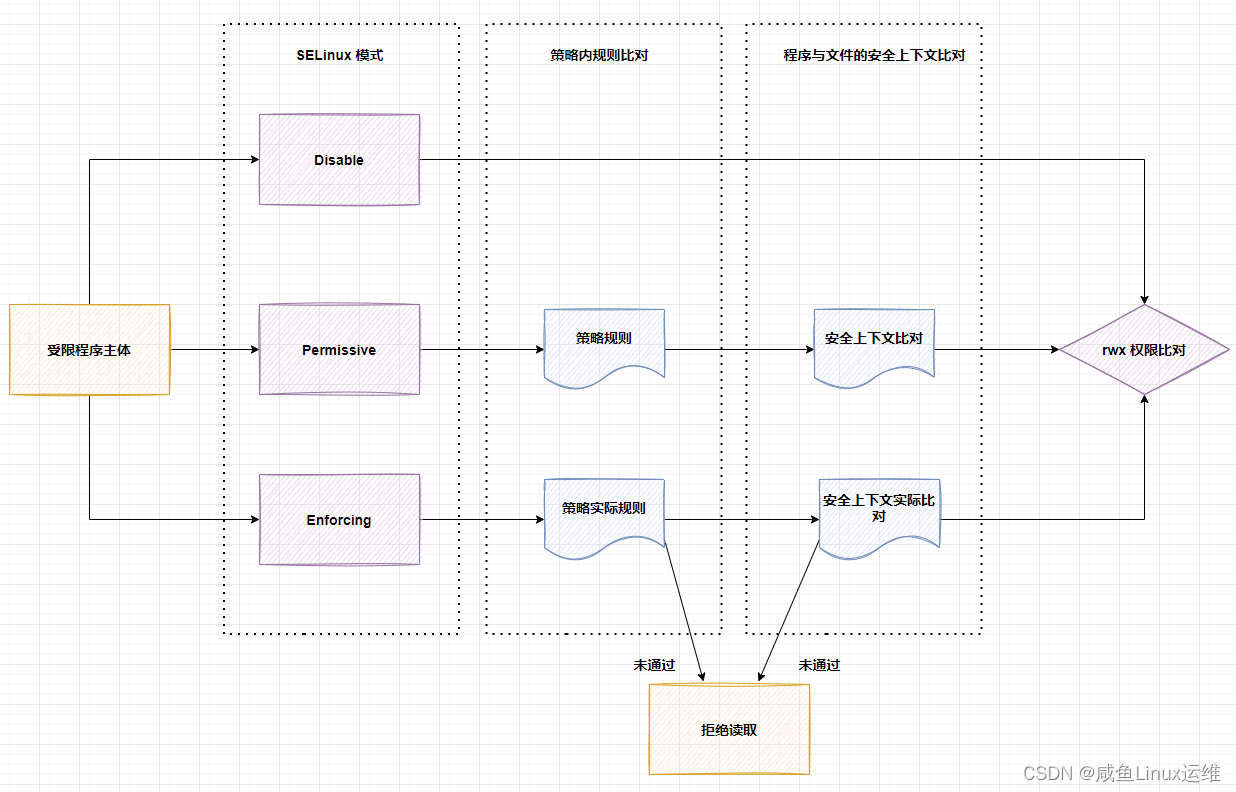
SELinux 入门 pt.2
哈喽大家好,我是咸鱼 在《SELinux 入门 pt.1》中,咸鱼向各位小伙伴介绍了 SELinux 所使用的 MAC 模型、以及几个重要的概念(主体、目标、策略、安全上下文) 我们还讲到: 对于受 SELinux 管制的进程,会先…...

函数(个人学习笔记黑马学习)
1、函数定义 #include <iostream> using namespace std;int add(int num1, int num2) {int sum num1 num2;return sum; }int main() {system("pause");return 0; } 2、函数的调用 #include <iostream> using namespace std;int add(int num1, int num2…...
《Flink学习笔记》——第五章 DataStream API
一个Flink程序,其实就是对DataStream的各种转换,代码基本可以由以下几部分构成: 获取执行环境读取数据源定义对DataStream的转换操作输出触发程序执行 获取执行环境和触发程序执行都属于对执行环境的操作,那么其构成可以用下图表示…...

Vue3.0 新特性以及使用变更总结
Vue3.0 在2020年9月正式发布了,也有许多小伙伴都热情的拥抱Vue3.0。去年年底我们新项目使用Vue3.0来开发,这篇文章就是在使用后的一个总结, 包含Vue3新特性的使用以及一些用法上的变更。 图片.png 为什么要升级Vue3 使用Vue2.x的小伙伴都熟悉…...

ToBeWritten之VSOC安全运营
也许每个人出生的时候都以为这世界都是为他一个人而存在的,当他发现自己错的时候,他便开始长大 少走了弯路,也就错过了风景,无论如何,感谢经历 转移发布平台通知:将不再在CSDN博客发布新文章,敬…...

2023爱分析·一站式通信解决方案市场厂商评估报告:牛信云
[图片] 01 中国企业出海发展背景及阶段 出海背景:出海,对中国企业而言,并不陌生。从最初的贸易型出海,到制造业崛起,再到互联网、移动互联网产业腾飞,中国企业在出海道路上走的越发稳健。行业也从最初的家电…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...

TJCTF 2025
还以为是天津的。这个比较容易,虽然绕了点弯,可还是把CP AK了,不过我会的别人也会,还是没啥名次。记录一下吧。 Crypto bacon-bits with open(flag.txt) as f: flag f.read().strip() with open(text.txt) as t: text t.read…...

基于开源AI智能名片链动2 + 1模式S2B2C商城小程序的沉浸式体验营销研究
摘要:在消费市场竞争日益激烈的当下,传统体验营销方式存在诸多局限。本文聚焦开源AI智能名片链动2 1模式S2B2C商城小程序,探讨其在沉浸式体验营销中的应用。通过对比传统品鉴、工厂参观等初级体验方式,分析沉浸式体验的优势与价值…...

链式法则中 复合函数的推导路径 多变量“信息传递路径”
非常好,我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题,统一使用 二重复合函数: z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y)) 来全面说明。我们会展示其全微分形式(偏导…...

