算法笔记:KD树
1 引入原因
- K近邻算法需要在整个数据集中搜索和测试数据x最近的k个点,如果一一计算,然后再排序,开销过大
- 引入KD树的作用就是对KNN搜索和排序的耗时进行改进
2 KD树
2.1 主体思路
- 以空间换时间,利用训练样本集中的样本点,沿各维度依次对k维空间进行划分,建立二叉树
- 利用分治思想提高算法搜索效率
- 二分查找的算法复杂度是O(logN)
,KD树的搜索效率与之接近(取决于所构造kd-tree是否接近平衡树)
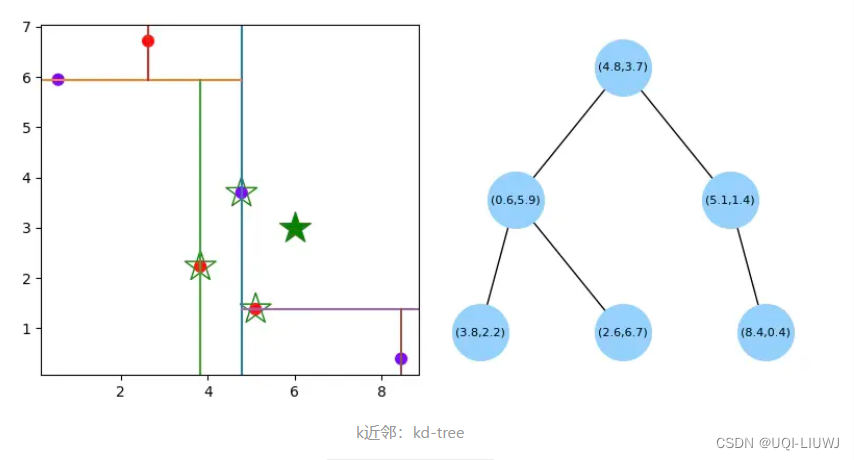
- 上图为为训练样本对空间的划分以及对应的kd树
- 绿色实心五角星为测试样本,通过kd-tree的搜索算法,快速找到与其最近邻的3个训练样本点(空心五角星标注的点)
2.2 KD树的建立
2.2.1 以一个例子引入
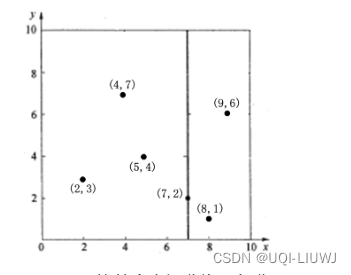
- 比如我有6个点:(2,3),(4,7),(5,4),(7,2),(8,1),(9,6)
- 1) 数据有两个维度,分别计算x,y方向上数据的方差
- x方向上的方差最大
- ——>先沿着X轴方向进行split
- 注:这一步也可以不要,因为KD树适用的问题大多是维度小于20的,所以按照维度顺序一个一个来也没有问题
- 2)根据x轴方向的值2,5,9,4,8,7排序选出中位数为7
- x≤7的和x >7的被分开了
- x≤7的和x >7的被分开了
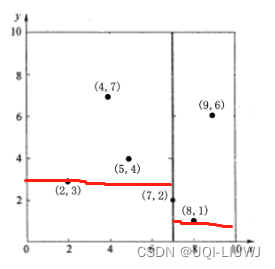
- 3) 被分开的左半区和右半区分别选出y轴方向的中位数(偶数选小的那个)
- 4)左上方三个点再根据x轴分一刀(其他三个区域已经各只剩一个点了)
- 最终得到的KD树
2.2.2 伪代码
def kd_tree_construct:input: x: 训练样本集dim: 当前节点的分割维度(子节点的分割维度=(dim+1)%样本的维度)output: node: 构造好的kd tree的根节点if 只有一个数据点:创建一个叶子结点node包含这一单一的点node.point = x[0]node.son1 = Nonenode.son2 = Nonereturn nodeelse:记dim维度上的中位点为x(对x中的数据按dim维排序,取中位点,偶数个则取较小的那个)记xl为左集合(dim维小于p点的所有点)记xr为右集合(dim维大于p点的所有点)创建带有两个孩子的node:node.point = pnode.son1 = fit_kd_tree(xl)node.son2 = fit_kd_tree(xr)return node2.3 KD树上的最近邻查找
2.3.1 伪代码
def kd_tree_search:global:Q, 缓存k个最近邻点(初始时包含一个无穷远点)q, 与Q对应,保存Q中各点与测试点的距离input: k, 寻找k个最近邻t, 测试点node, 当前节点(一开始时根节点)dim, 当前节点的分割维度(子节点的分割维度=(dim+1)%数据点的维度)output: 无if distance(t, node.point) < max(q):将node.point添加到Q,并同步更新q若Q内超过k个近邻点,则移出与测试点距离最远的那个点,并同步更新qif t[dim]-max(q) < node.point[dim]:kd_tree_search(k,t,node.son1)if t[dim]+max(q) > node.point[dim]:kd_tree_search(k,t,node.son2)
2.3.1 以一个例子开始
2.3.1.1 例子1
搜索(2.1,3.1)
记k=1
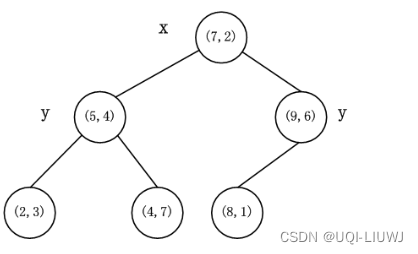
- 第1步:将(7,2)加入Q中,maxq=5.02,更新Q
- 2.1-5.02≤7
- 搜索左儿子
- 第2步:将(5.4)加入Q中,maxq=3.04,更新Q
- 3.1-3.04≤4
- 搜索下儿子
- 第3步:将(2,3)加入Q中,maxq=0.1414,更新Q
- 已经是叶子节点了,结束
- 3.1-3.04≥4
- 搜索上儿子
- 第4步:将(4,7)加入Q中,maxq=4.338>0.1414,不更新Q,仍为0.1414
- 已经是叶子节点了,结束
- 3.1-3.04≤4
- 2.1-5.02≥7
- 搜索右儿子
- 第5步,将(9,6)加入Q中,maxq=7.484>0.1414,不更新Q,仍为0.1414
- 3.1+7.484>6
- 搜索上儿子
- 没有上儿子,结束
- 2.1-5.02≤7
- 算法结束,最近的点是(2,3),q=0.1414
2.3.1.2 例子2 回溯时改变最近邻点
假设我们要查询的点是2,4.5
同样记k=1

- 第1步:将(7,2)加入Q中,maxq=5.59,更新Q
- 2-5.59≤7
- 搜索左儿子
- 第2步:将(5.4)加入Q中,maxq=3.04,更新Q
- 4.5-3.04≤4
- 搜索下儿子
- 第3步:将(2,3)加入Q中,maxq=1.5,更新Q
- 4.5+3.04≥4
- 搜索上儿子
- 第4步:将(4,7)加入Q中,maxq=3.20>1.5,不更新Q,仍为1.5
- 4.5-3.04≤4
- 2+5.59 >7
- 搜索右儿子
- 第5步,将(9,6)加入Q中,maxq=7.16>1.5,不更新Q,仍为1.5
- 4.5+7.16>6
- 搜索上儿子
- 没有上儿子,结束
- 4.5+7.16>6
- 2-5.59≤7
- 算法结束,最近的点是(2,3),距离为1.5
参考内容:KNN的核心算法kd-tree和ball-tree - 简书 (jianshu.com)
k-d tree算法 - J_Outsider - 博客园 (cnblogs.com)
相关文章:

算法笔记:KD树
1 引入原因 K近邻算法需要在整个数据集中搜索和测试数据x最近的k个点,如果一一计算,然后再排序,开销过大 引入KD树的作用就是对KNN搜索和排序的耗时进行改进 2 KD树 2.1 主体思路 以空间换时间,利用训练样本集中的样本点&…...
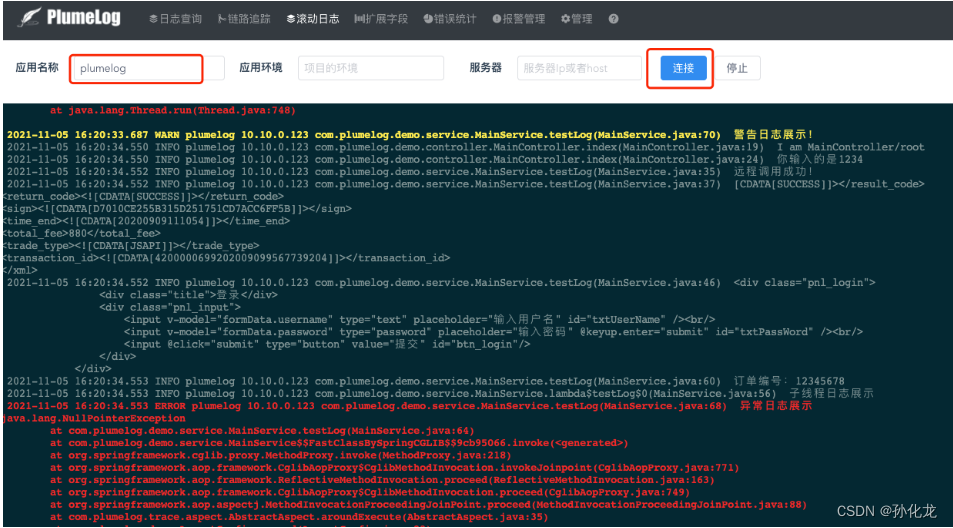
plumelog介绍与应用-一个简单易用的java分布式日志系统
官方文档:http://www.plumelog.com/zh-cn/docs/FASTSTART.html 简介 无代码入侵的分布式日志系统,基于log4j、log4j2、logback搜集日志,设置链路ID,方便查询关联日志基于elasticsearch作为查询引擎高吞吐,查询效率高全…...

百度网盘删除“我的应用数据”文件夹
百度网盘删除“我的应用数据”文件夹电脑端方法-2023.2.27成功 - 哔哩哔哩 (bilibili.com) 百度网盘怎样删除我的应用数据文件夹-手机端方法-2023.3.24日成功 - 哔哩哔哩 (bilibili.com)...

多店铺智能客服,助力店铺销量倍增
近年来电商发展得非常快速,市场竞争也是愈发激烈了。商家不仅需要提高产品和服务的质量,还要争取为自己获取更多的曝光,以此来分散运营的风险和降低经营的成本,所以越来越多的商家也开始转向多平台多店铺运营。但即使运营多个平台…...

会话跟踪技术
cookie 是通过在浏览器第一次请求服务器时,在响应中放入cookie,浏览器接收到cookie后保存在本地,之后每次请求服务器时都将cookie携带到请求头中,用来验证用户身份与状态等。 缺点: 移动端app没有cookiecookie保存在…...
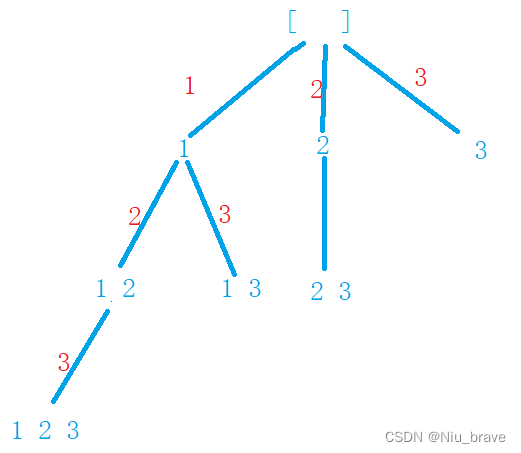
递归算法学习——子集
目录 一,题目解析 二,例子 三,题目接口 四,解题思路以及代码 1.完全深度搜索 2.广度搜索加上深度优先搜索 五,相似题 1.题目 2.题目接口 3.解题代码 一,题目解析 给你一个整数数组 nums ,…...
)
学习笔记:ROS使用经验(ROS报错)
报错:进程崩溃 ] process has died [pid 734, exit code -5, cmd /root/catkin_ws/devel/lib/pose_graph/pose_graph __name:pose_graph __log:/root/.ros/log/31b0ae1c-3295-11ee-bda9-02429b5737dc/pose_graph-5.log]. log file: /root/.ros/log/31b0ae1c-3295-11…...
)
设计模式二十四:访问者模式(Visitor Pattern)
用于将数据结构与数据操作分离,使得可以在不修改数据结构的情况下,定义新的操作。访问者模式的核心思想是,将数据结构和操作进行解耦,从而使得新增操作时不必修改数据结构,只需添加新的访问者。主要目的是在不改变数据…...
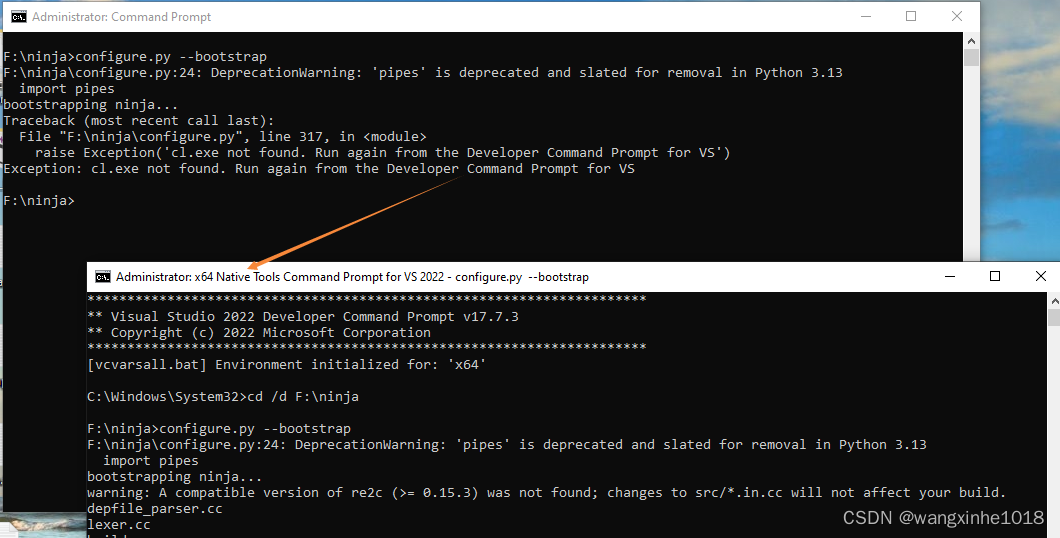
使用gn+Ninja构建项目
使用下载编译好的gn和ninja报错 先下载了gn的源码[gn.googlesource.com/gn],然后编译报错,就直接下载了了编译号的gn和Ninja,然后写了Helloworld应用的BUILD.gn,然后将"gn\examples\simple_build\build"拷贝至当前目录…...
VMware虚拟机连不上网络
固定ip地址 进入网络配置文件 cd /etc/sysconfig/network-scripts 打开文件 vi ifcfg-ens33 编辑 BOOTPROTO设置为static,有3个值(decp、none、static) BOOTPROTO"static" 打开网络 ONBOOT"yes" 固定ip IPADDR1…...
安防视频监控/视频集中存储/云存储平台EasyCVR平台无法取消共享通道该如何解决?
视频汇聚/视频云存储/集中存储/视频监控管理平台EasyCVR能在复杂的网络环境中,将分散的各类视频资源进行统一汇聚、整合、集中管理,实现视频资源的鉴权管理、按需调阅、全网分发、云存储、智能分析等,视频智能分析平台EasyCVR融合性强、开放度…...

算法通关村-----如何基于数组和链表实现栈
实现栈的基本方法 push(T t)元素入栈 T pop() 元素出栈 Tpeek() 查看栈顶元素 boolean isEmpty() 栈是否为空 基于数组实现栈 import java.util.Arrays;public class ArrayStack<T> {private Object[] stack;private int top;public ArrayStack() {this.stack new…...
day-05 TCP半关闭 ----- DNS ----- 套接字的选项
一、优雅的断开套接字连接 之前套接字的断开都是单方面的。 (一)基于TCP的半关闭 Linux的close函数和windows的closesocket函数意味着完全断开连接。完全断开不仅不能发送数据,从而也不能接收数据。在某些情况下,通信双方的某一方…...

区块链金融项目怎么做?
区块链技术的兴起引发了金融领域的变革,为金融行业带来了前所未有的机遇与挑战。在这个快速发展的领域中,如何在区块链金融领域做出卓越的表现?本文将从专业性和思考深度两个方面,探讨区块链金融的发展路径,并为读者提…...

Redis与数据库保持一致
参考链接 先更新数据库,再更新redis 存在漏洞,如果更新Redis失败,仍然会导致不一致 先删Redis,再更新数据库并同步数据到Redis 存在漏洞,多线程情况下,线程1删除redis后,还是有可能被其他线程读取旧的数据…...
idea中vue项目 npm安装插件后node modules中找不到
从硬盘中重新加载一下...

已知两地经纬度,计算两地直线距离
文章目录 1 原理公式2 代码实现2.1 JavaScript2.2 C2.3 Python2.4 MATLAB 1 原理公式 在地球上,计算两点之间的直线距离通常使用地理坐标系(例如WGS84)。计算两地直线距离的公式是根据经纬度之间的大圆距离(Great Circle Distanc…...

我想开通期权?如何开通期权账户?
场内期权的合约由交易所统一标准化定制,大家面对的同一个合约对应的价格都是一致的,比较公开透明,期权开户当天不能交易的,期权开户需要满足20日日均50万及半年交易经验即可操作,下文科普我想开通期权?如何…...

ChatGPT对软件测试的影响
ChatGPT 是一个经过预训练的 AI 语言模型,可以通过聊天的方式回答问题,或者与人闲聊。它能处理的是文本类的信息,输出也只能是文字。它从我们输入的信息中获取上下文,结合它被训练的大模型,进行分析总结,给…...
minion在ubuntu上的搭建步骤
在Ubuntu上搭建MinIO可以按照以下步骤进行: 下载MinIO服务器二进制文件: 通过浏览器访问 https://min.io/download 或使用以下命令获取最新的MinIO二进制文件:wget https://dl.min.io/server/minio/release/linux-amd64/minio赋予二进制文件…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...