(笔记五)利用opencv进行图像几何转换
参考网站:https://docs.opencv.org/4.1.1/da/d6e/tutorial_py_geometric_transformations.html
(1)读取原始图像和标记图像
import cv2 as cv
import numpy as np
from matplotlib import pyplot as pltpath = r"D:\data\flower.jpg"
img = cv.imread(path)
img = cv.cvtColor(img, cv.COLOR_BGR2RGB)# 拷贝图像
img1 = np.copy(img)
img1[100:105, 100:105, :] = [255, 0, 0] # main point is (103, 103)
img1[100:105, 150:155, :] = [255, 0, 0] # main point is (103, 153)
img1[150:155, 100:105, :] = [255, 0, 0] # main point is (153, 103)
img1[150:155, 150:155, :] = [255, 0, 0] # main point is (153, 153)
plt.figure(12)
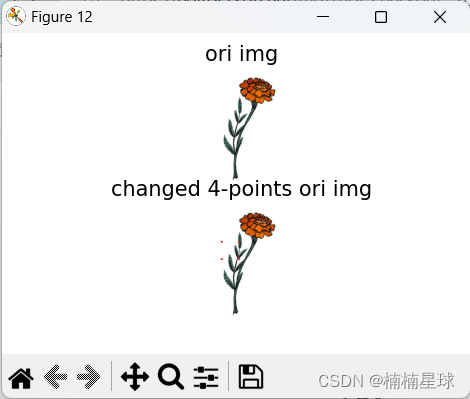
plt.subplot(211), plt.imshow(img), plt.title('ori img'), plt.axis('off')
plt.subplot(212), plt.imshow(img1), plt.title('changed 4-points ori img'), plt.axis('off')
# plt.show()
(2)改变图像分辨率
# 改变分辨率
img2 = np.copy(img)
# dsize = None,fx是x相对于原来的x要改变的比例,同理y
img3 = cv.resize(img2, None, fx=0.1, fy=0.1, interpolation=cv.INTER_CUBIC)
img4 = cv.resize(img2, None, fx=10, fy=10, interpolation=cv.INTER_CUBIC)
plt.figure(3)
plt.subplot(311), plt.imshow(img), plt.title('ori img resolution:' + str(img.shape[0:2])), plt.axis('off')
plt.subplot(312), plt.imshow(img3), plt.title('0.1 times resolution:' + str(img3.shape[0:2])), plt.axis('off')
plt.subplot(313), plt.imshow(img4), plt.title('10 times resolution:' + str(img4.shape[0:2])), plt.axis('off')
# plt.show()

(3)平移图像
核心函数:cv.warpAffine(img, M, (col, row))
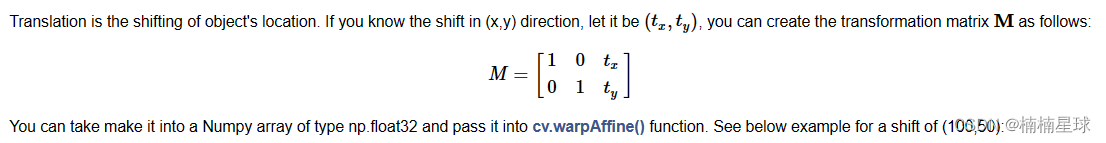
# 图像平移
img5 = np.copy(img)
row, col, sp = img5.shape
M1 = np.float32([[1, 0, 100], [0, 1, 50]]) # x平移100,y平移50
print('图像平移:')
print('图像平移所计算的转换矩阵为:', M1)
img6 = cv.warpAffine(img5, M1, (col, row)) # warpAffine函数利用转移矩阵平移
plt.figure(4)
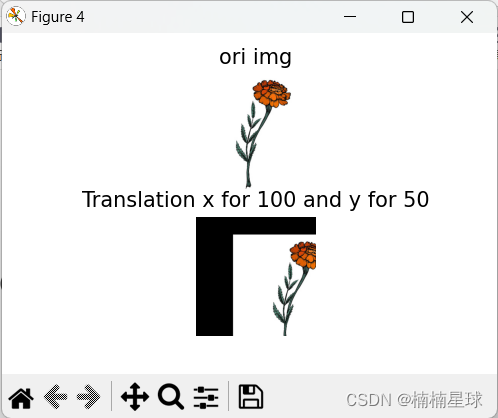
plt.subplot(211), plt.imshow(img), plt.title('ori img'), plt.axis('off')
plt.subplot(212), plt.imshow(img6), plt.title('Translation x for 100 and y for 50'), plt.axis('off')
# plt.show()

(4)图像旋转
核心函数:M=cv.getRotationMatrix2D(((旋转中心坐标(x,y)), 旋转角度, 相向尺度因子)
cv.warpAffine(img, M, (col, row))

# 图像旋转
img7 = np.copy(img)
# 图像中心,图像旋转角度,图像同向比例因子
M2 = cv.getRotationMatrix2D(((col - 1) / 2, (row - 1) / 2), 45, 1)
M3 = cv.getRotationMatrix2D(((col - 1) / 2, (row - 1) / 2), 0, 3)
print('图像旋转:')
print('旋转一的转换矩阵:', M2)
print('旋转二的转换矩阵:', M3)
img8 = cv.warpAffine(img7, M2, (col, row))
img9 = cv.warpAffine(img7, M3, (col, row))
plt.figure(5)
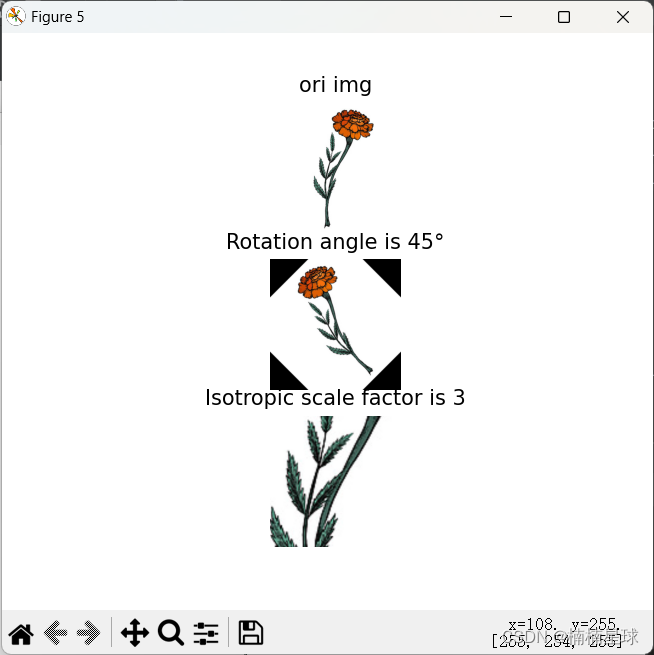
plt.subplot(311), plt.imshow(img), plt.title('ori img'), plt.axis('off')
plt.subplot(312), plt.imshow(img8), plt.title('Rotation angle is 45°'), plt.axis('off')
plt.subplot(313), plt.imshow(img9), plt.title('Isotropic scale factor is 3'), plt.axis('off')
# plt.show()

(5)图像仿射变换
核心函数:M=cv.getAffineTransform(原图三个点坐标, 转换图三个点坐标)
cv.warpAffine(img, M, (col, row))

# 仿射变换
img10 = np.copy(img1)
points_one = np.float32([[103, 103], [103, 153], [153, 103]]) # 原始图像三个点坐标
points_two = np.float32([[10, 100], [100, 10], [150, 275]]) # 仿射变换目标图像的三个点坐标
M4 = cv.getAffineTransform(points_one, points_two)
print('仿射变换:')
print('仿射变换的转换矩阵:', M4)
img11 = cv.warpAffine(img10, M4, (col, row))
plt.figure(6)
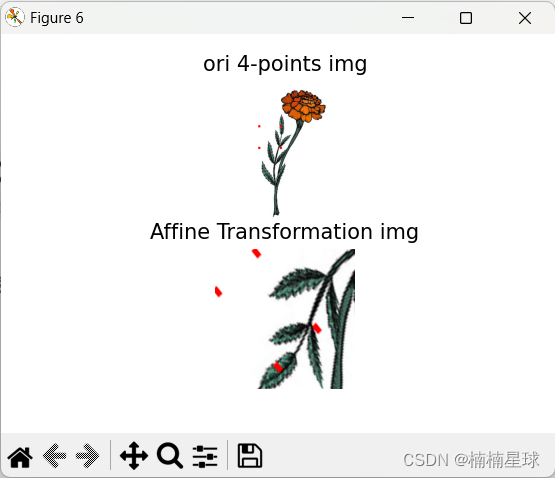
plt.subplot(211), plt.imshow(img1), plt.title('ori 4-points img'), plt.axis('off')
plt.subplot(212), plt.imshow(img11), plt.title('Affine Transformation img'), plt.axis('off')
# plt.show()
(6)图像透射变换
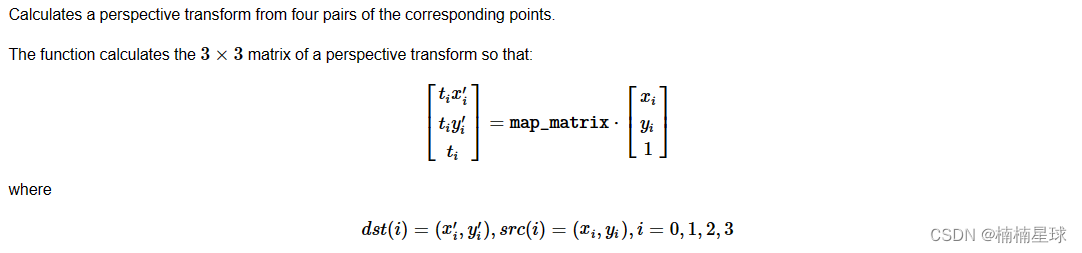
核心函数:M=cv.getPerspectiveTransform(原图四个点坐标,转换图像四个点坐标 )
cv.warpPerspective(img, M, (转换图长宽))
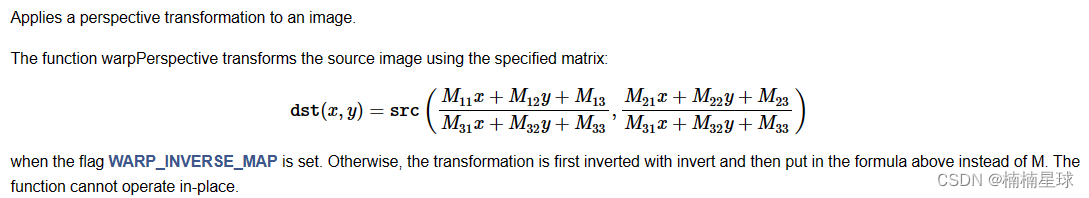
# 透射变换
img12 = np.copy(img1)
points_one_one = np.float32([[103, 103], [103, 153], [153, 103], [153, 153]]) # 原始图像四个点坐标
points_two_two = np.float32([[0, 0], [0, 300], [300, 0], [300, 300]]) # 透射变换目标图像的四个点坐标
M5 = cv.getPerspectiveTransform(points_one_one, points_two_two)
print('透射变换:')
print('透射变换的转换矩阵:', M5)
# img12为要转换的图像,M5为透射变换的转换矩阵,dsize为目标图像大小
img13 = cv.warpPerspective(img12, M5, (300, 300))
plt.figure(7)
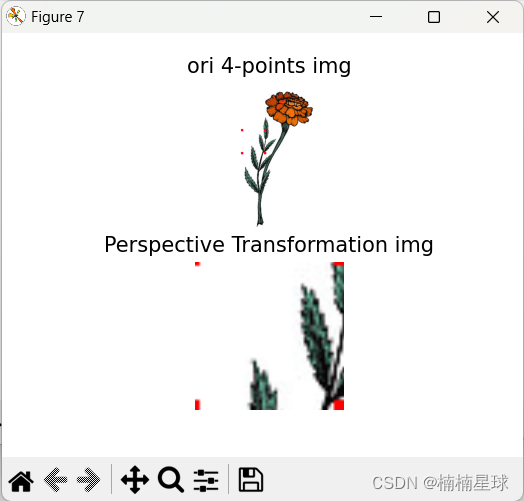
plt.subplot(211), plt.imshow(img1), plt.title('ori 4-points img'), plt.axis('off')
plt.subplot(212), plt.imshow(img13), plt.title('Perspective Transformation img'), plt.axis('off')
plt.show()

相关文章:

(笔记五)利用opencv进行图像几何转换
参考网站:https://docs.opencv.org/4.1.1/da/d6e/tutorial_py_geometric_transformations.html (1)读取原始图像和标记图像 import cv2 as cv import numpy as np from matplotlib import pyplot as pltpath r"D:\data\flower.jpg&qu…...
【Flutter】Flutter 使用 fluttertoast 实现显示 Toast 消息
【Flutter】Flutter 使用 fluttertoast 实现显示 Toast 消息 文章目录 一、前言二、安装和基础使用三、不同平台的支持情况四、如何自定义 Toast五、在实际业务中的应用六、完整的业务代码示例(基于 Web 端)七、总结 一、前言 在这篇文章中,…...
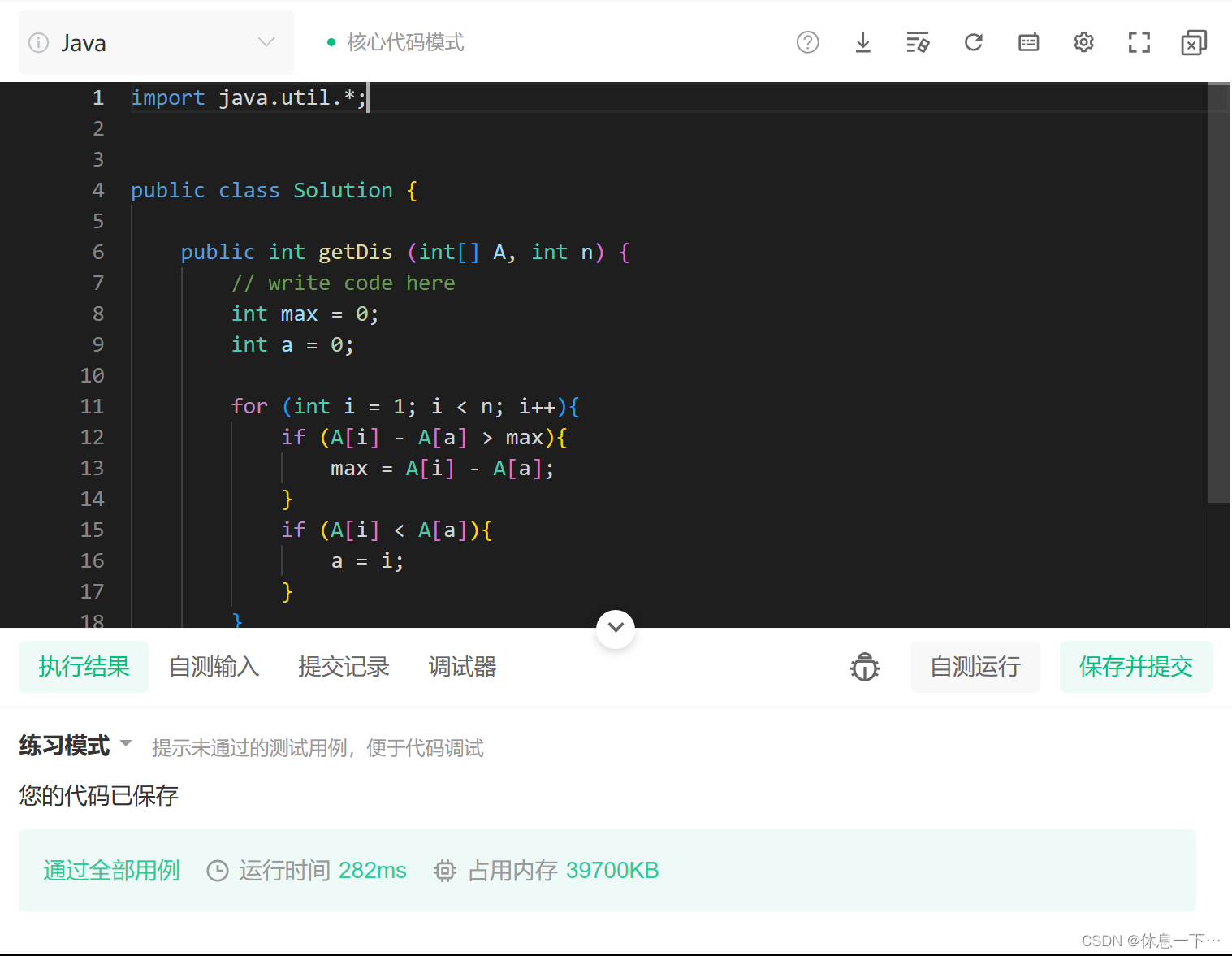
nowcoder NC236题 最大差值
目录 题目描述: 示例1 示例2 题干解析: 暴力求解: 代码展示: 优化: 代码展示: 题目跳转https://www.nowcoder.com/practice/a01abbdc52ba4d5f8777fb5dae91b204?tpId128&tqId33768&ru/exa…...
TCP/IP五层模型、封装和分用
1.网络通信基础2.协议分层OSI七层协议模型TCP/IP五层/四层协议模型【重点】 3. 封装&分用 1.网络通信基础 IP地址:表示计算机的位置,分源IP和目标IP;举个例子:买快递,商家从上海发货,上海就是源IP&…...

LeetCode 面试题 01.08. 零矩阵
文章目录 一、题目二、C# 题解 一、题目 编写一种算法,若M N矩阵中某个元素为0,则将其所在的行与列清零。 点击此处跳转题目。 示例 1: 输入: [ [1,1,1], [1,0,1], [1,1,1] ] 输出: [ [1,0,1], [0,0,0], [1,0,1] ] 示…...

Qt应用开发(基础篇)——进度条 QProgressBar
一、前言 QProgressBar类继承于QWidget,是一个提供了横向或者纵向进度条的小部件。 QProgressBar进度条一般用来显示用户某操作的进度,比如烧录、导入、导出、下发、上传、加载等这些需要耗时和分包的概念,让用户知道程序还在正常的执行中。 …...
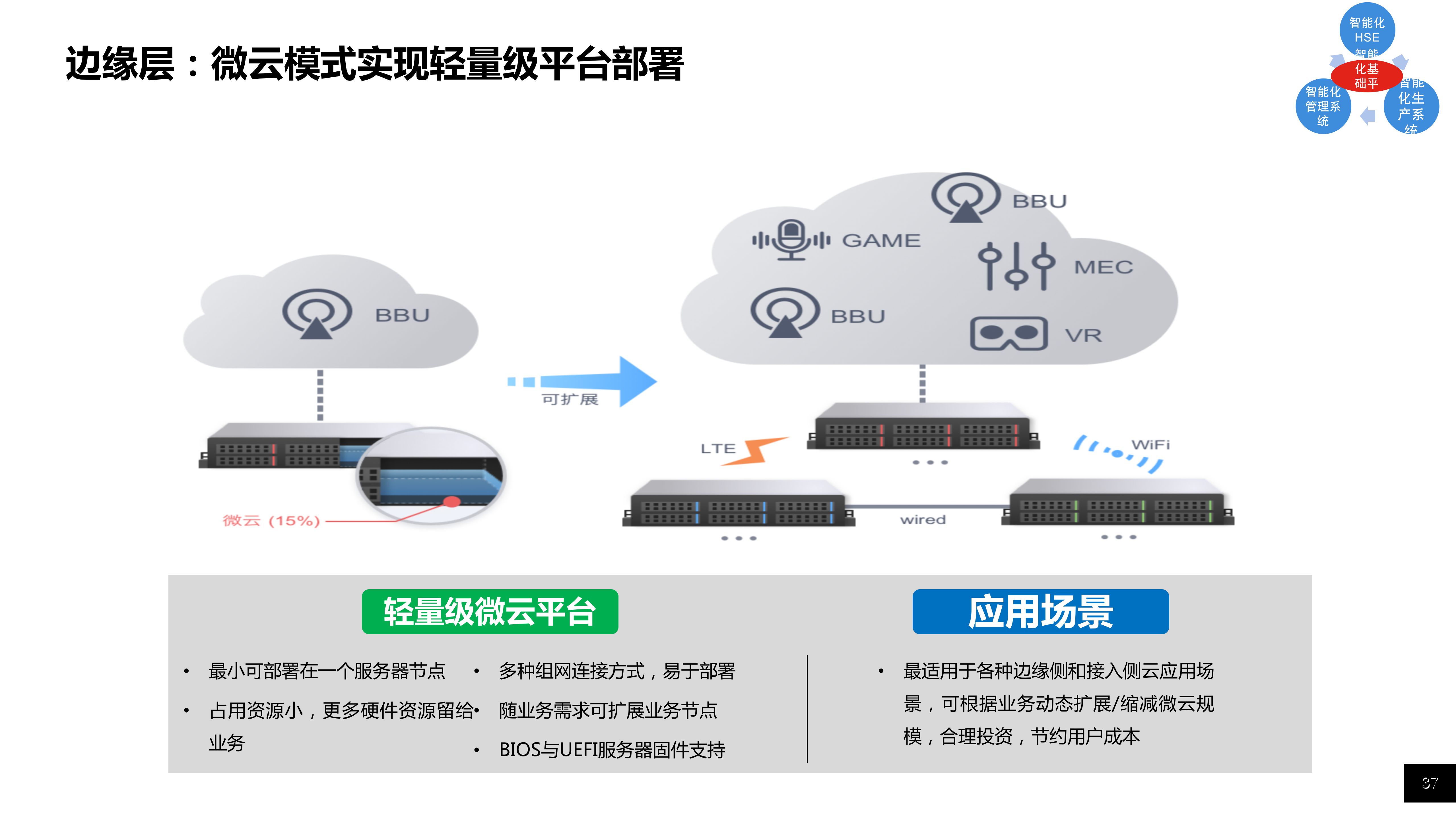
108页石油石化5G智慧炼化厂整体方案PPT
导读:原文《108页石油石化5G智慧炼化厂整体方案PPT》(获取来源见文尾),本文精选其中精华及架构部分,逻辑清晰、内容完整,为快速形成售前方案提供参考。以下是部分内容,...

Codeforces 1625E2 括号树 + BIT
题意 传送门 Codeforces 1625E2 Cats on the Upgrade (hard version) 题解 首先利用栈将原始字符串转换为合法的 RBS,不能匹配的括号设为 ‘.’。根据匹配的括号序列构造树,具体而言,遇到左括号,则新建节点向下递归,…...

PHP命令行CLI的使用
PHP命令行界面 PHP命令行界面(CLI)是一种使用命令行(终端)来运行PHP脚本的方式,与在Web服务器环境下运行PHP不同。CLI提供了一种与操作系统交互的方式,能够在命令行中直接执行PHP代码。 以下是一些与PHP命…...

近期嵌软线下笔试题记录
1、以下代码的输出结果是? #include <stdio.h> #include <string.h>int main() {int a,b,c,d;a 10;b a; //a先赋值给b,然后自增1c a; //a自增1后赋值给cd 10*a; //先进行运算然后a自增1printf("b,c,d:%d…...
基于MYSQL的主从同步和读写分离
目录 一.完成MySQL主从同步(一主两从) 1.主库配置 2.建立同步账号 3.锁表设置只读 4.备份数据库数据 5.主库备份数据上传到从库 6.从库上还原备份 7.解锁 8.从库上设定主从同步 9.启动从库同步开关 10.检查状态 二.基于MySQL一主两从配置&…...

java八股文面试[多线程]——合适的线程数是多少
知识来源: 【并发与线程】 合适的线程数量是多少?CPU 核心数和线程数的关系?_哔哩哔哩_bilibili 【2023年面试】程序开多少线程合适_哔哩哔哩_bilibili...

Linux系统下vim常用命令
一、基础命令: v:可视模式 i:插入模式 esc:命令模式下 :q :退出 :wq :保存并退出 ZZ:保存并退出 :q! :不保存并强制退出二、在Esc下: dd : 删除当前行 yy:复制当前行 p:复制已粘贴的文本 u:撤销上一步 U:…...

【2023】LeetCode HOT 100——链表
目录 1. 相交链表1.1 C++实现1.2 Python实现1.3 时空分析2. 反转链表2.1 C++实现2.2 Python实现2.3 时空分析3. 回文链表3.1 C++实现3.2 Python实现3.3 时空分析4. 环形链表4.1 C++实现4.2 Python实现4.3 时空分析5. 环形链表 II5.1 C++实现5.2 Python实现...
智能井盖传感器,物联网智能井盖系统
随着城市人口的不断增加和城市化进程的不断推进,城市基础设施的安全和可靠性变得愈发重要,城市窨井盖作为城市基础设施重要组成部分之一,其安全性事关城市安全有序运行和居民生产生活安全保障。 近年来,各地都在加强城市窨井盖治理…...

C语言三子棋解析
目录(标2的是我自己写的一堆问题不知道怎么改) 开始菜单1打印棋盘1玩家下棋1电脑下棋1判断输赢1开始菜单2打印棋盘2选择先后2玩家下棋2电脑下棋2判断输赢2完整代码文件else.h文件else.c文件test.c 开始菜单1 void menu()//打印菜单 {printf("*****…...
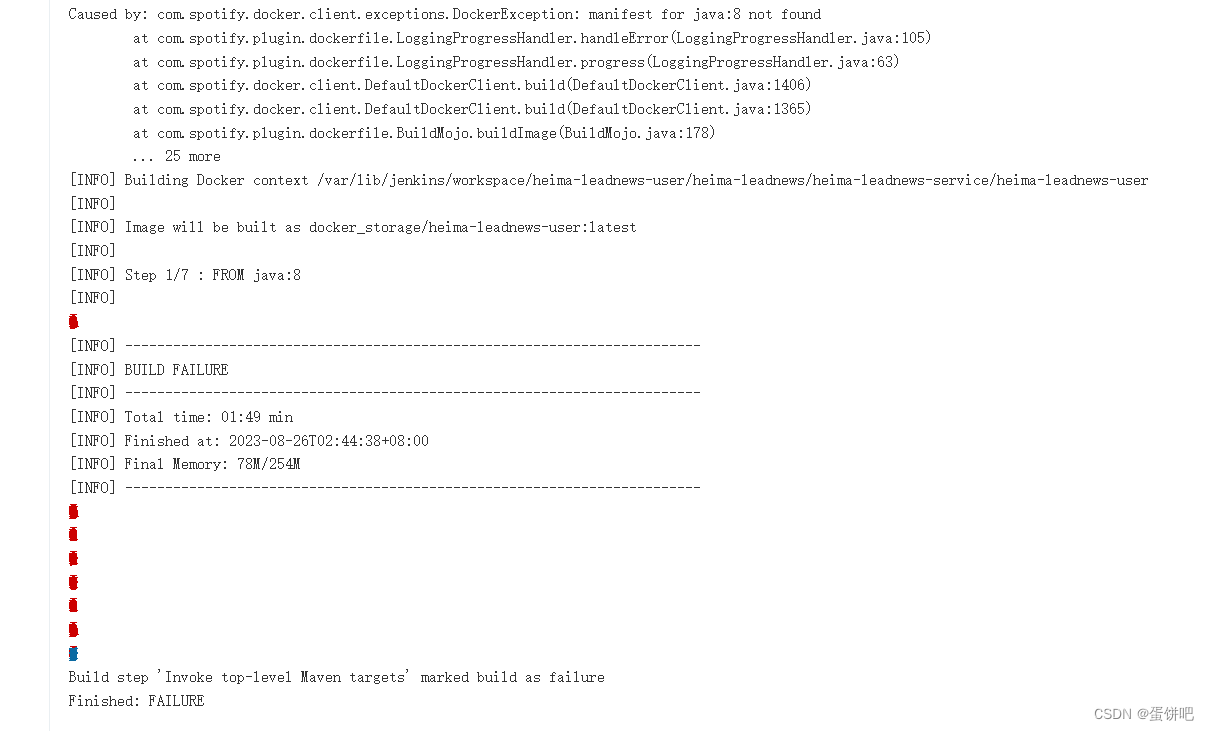
【Jenkins打包服务,Dockerfile报错:manifest for java : 8 not fourd】
1、问题描述 Jenkins打包服务运行dockerfile里的FROM java:8报错manifest for java : 8 not fourd Caused by: com.spotify. docker.client.exceptions.DockerException: manifest for java:8 not found2、解决方法 在网上查找许多方法后得出这是由于Docker官方已经弃用java…...
读SQL学习指南(第3版)笔记06_连接和集合
1. 连接 1.1. 笛卡儿积 1.1.1. 交叉连接(cross join) 1.1.2. 查询并没有指定两个数据表应该如何连接,数据库服务器就生成了笛卡儿积 1.1.2.1. 两个数据表的所有排列组合 1.1.3. 很少会用到(至少不会特意用到) 1.…...

C#学习,结构,面向对象,类
结构和类 结构是从过程化程序设计中保留下来的一种数据类型,类则是面向对象程序设计中最基本的、也是最重要的概念。 结构 结构是一种值类型,通常用来封装一组相关的变量,结构中可以包含构造函数、变量、字段、方法、属性、运算符、事件和…...

【PHP】文件操作
文章目录 文件编程的必要性目录操作其它目录操作递归遍历目录PHP5常见文件操作函数PHP4常见文件操作函数其他文件操作函数 文件编程的必要性 文件编程指利用PHP代码针对文件(文件夹)进行增删改查操作。 在实际开发项目中,会有很多内容&…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...
