LeetCode1049. 最后一块石头的重量 II
1049. 最后一块石头的重量 II
文章目录
- [1049. 最后一块石头的重量 II](https://leetcode.cn/problems/last-stone-weight-ii/)
- 一、题目
- 二、题解
- 方法一:01背包二维数组
- 算法思路
- 具体实现
- 方法二:01背包一维数组
一、题目
有一堆石头,用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。
每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x <= y。那么粉碎的可能结果如下:
- 如果
x == y,那么两块石头都会被完全粉碎; - 如果
x != y,那么重量为x的石头将会完全粉碎,而重量为y的石头新重量为y-x。
最后,最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下,就返回 0。
示例 1:
输入:stones = [2,7,4,1,8,1]
输出:1
解释:
组合 2 和 4,得到 2,所以数组转化为 [2,7,1,8,1],
组合 7 和 8,得到 1,所以数组转化为 [2,1,1,1],
组合 2 和 1,得到 1,所以数组转化为 [1,1,1],
组合 1 和 1,得到 0,所以数组转化为 [1],这就是最优值。
示例 2:
输入:stones = [31,26,33,21,40]
输出:5
提示:
1 <= stones.length <= 301 <= stones[i] <= 100
二、题解
方法一:01背包二维数组
算法思路
01背包问题回顾
在01背包问题中,我们有一组物品,每个物品有两个属性:重量和价值。背包有一个固定的容量,我们的目标是在不超过背包容量的情况下,选择物品放入背包,使得放入的物品总价值最大。
我们可以将这个问题的状态定义为 dp[i][j],表示在前 i 个物品中,背包容量为 j 的情况下,可以获得的最大价值。状态转移方程可以表示为:
dp[i][j] = max(dp[i-1][j], dp[i-1][j-weight[i]] + value[i])
将题目映射到01背包
现在我们回到题目中,虽然题目描述中没有直接提到背包,但我们可以通过观察发现类似的特性:我们要将石头分成两堆,使得两堆的重量差尽量小。
在01背包问题中,我们选择物品放入背包的状态是离散的:要么放入,要么不放入。在本题中,我们可以类比,将石头看作是我们要选择放入背包的“物品”,每块石头的重量看作是物品的“重量”。我们要将石头分成两堆,使得两堆的重量差尽量小,相当于在一个背包的容量为总重量的一半时,选择一些石头放入背包,使得背包中的石头总重量尽量接近总重量的一半。
(这里的背包容量就对应着总重量的一半,而每块石头的重量和价值相同)。这就是为什么我们能够将这个问题映射到01背包问题。
具体实现
-
状态定义: 定义一个二维数组
dp[i][j],表示在前i块石头中,能否找到一种分法,使得其中一组的总重量恰好为j。这里i的范围是从0到石头的总数,j的范围是从0到总重量的一半(因为我们要将石头分成两组,两组的重量和不能超过总重量的一半,否则不符合题意)。 -
状态转移: 对于每一块石头,我们可以选择将其放入其中一组,或者不放入。如果我们不放入第
i块石头,那么问题就转化为在前i-1块石头中寻找一种分法,使得其中一组的总重量恰好为j。如果我们放入第i块石头,那么问题就转化为在前i-1块石头中寻找一种分法,使得其中一组的总重量恰好为j - stones[i]。综合考虑这两种情况,我们可以得到状态转移方程:
dp[i][j] = dp[i-1][j] || dp[i-1][j-stones[i]] -
边界条件: 初始化时,当只有一块石头可选时,如果这块石头的重量不超过
j,那么我们可以将其放入其中一组,否则不放入。 -
最终结果: 最终的答案应该是在所有可能的总重量
j中,找到最大的j,使得dp[n-1][j]为true(n为石头的总数)。然后最小可能的剩余重量就是sum - 2 * j。
根据上述思路,可以实现出解题代码:
class Solution {
public:int lastStoneWeightII(vector<int>& stones) {int sum = 0;for (int i = 0; i < stones.size(); i++) {sum += stones[i];}int n = stones.size();vector<vector<int>> dp(n, vector<int>(sum / 2 + 1, 0));// 初始化for (int i = 0; i <= sum / 2; i++) {if (stones[0] <= i) {dp[0][i] = stones[0];}}// 填写dp数组for (int i = 1; i < n; i++) {for (int j = 1; j <= sum / 2; j++) {if (stones[i] > j) {dp[i][j] = dp[i - 1][j];} else {dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - stones[i]] + stones[i]);}}}return sum - 2 * dp[n - 1][sum / 2];}
};
方法二:01背包一维数组
class Solution {
public:int lastStoneWeightII(vector<int>& stones) {int sum = 0;for (int i = 0; i < stones.size(); i++) {sum += stones[i];}vector<int> dp(sum/2+1, 0);// 填写dp数组for (int i = 0; i < stones.size(); i++) {for (int j = sum/2; j >= stones[i]; j--) { dp[j] = max(dp[j], dp[j-stones[i]] + stones[i]);} }return sum - 2 * dp[sum/2];}
};
Q:为什么 for (int j = sum/2; j >= stones[i]; j–)要倒序遍历?
A:我们从前往后遍历石头,同时从总重量的一半开始递减遍历,这是因为我们想在填写 dp[j] 时,基于之前的状态 dp[j-stones[i]] 进行更新。如果我们从小到大遍历 j,那么在填写 dp[j] 时,我们可能会使用当前石头的重量(stones[i]),而这就会导致重复使用同一块石头,与题意不符。
所以,倒序遍历 j 可以确保在填写 dp[j] 时,我们只会考虑之前的状态,而不会用到当前石头。这是为了避免在填写 dp[j] 时,使用当前石头导致重复计算的情况。
Q:为什么一定要先遍历石头重量这一行然后遍历重量那一列?
A:这是为了确保状态转移方程的正确性。让我们通过一个例子来理解。
假设我们有以下石头的重量:stones = [2, 7, 4]。
我们想要使用动态规划找到一种分法,使得其中一组的总重量尽量接近总重量的一半。在此例中,总重量是 2 + 7 + 4 = 13,所以我们希望找到一种分法,使得其中一组的重量接近 13 / 2 = 6。
现在,假设先遍历重量(j),再遍历石头(i)。在这种情况下,第一次遍历(j = sum/2,i从0到stones.size())后我们的动态规划状态数组如下所示:
stones = [2, 7, 4]
dp[i][j]:0 1 2 3 4 5 6 2: 0 0 0 0 0 0 4 7: 0 0 0 0 0 0 4 4: 0 0 0 0 0 0 4
在这种遍历顺序下,最后一列一直到最后都不会再更新了,显然是一个错误的遍历顺序。
相关文章:

LeetCode1049. 最后一块石头的重量 II
1049. 最后一块石头的重量 II 文章目录 [1049. 最后一块石头的重量 II](https://leetcode.cn/problems/last-stone-weight-ii/)一、题目二、题解方法一:01背包二维数组算法思路具体实现 方法二:01背包一维数组 一、题目 有一堆石头,用整数数…...

universal robot 机械臂 官方基本教程
https://academy.universal-robots.cn/modules/e-Series-core-track/Chinese/module3/story_html5.html?courseId2166&languageChinese 教程1 控制箱内部 包含: 主机板,SD卡,和安全控制板 安全控制板负责所有控制信息,包括…...

网络常见安全漏洞
引言 随着互联网的迅猛发展,网络安全问题日益严重。在网络世界中,各种常见的安全漏洞给人们的通信和数据安全带来了巨大的威胁。本文将介绍一些常见的网络安全漏洞,并提供一些防范措施。 1. XSS(跨站脚本攻击) 跨站…...

【JS案例】JS实现图片放大镜功能
JS案例图片放大镜 🌟效果展示 🌟HTML结构 🌟CSS样式 🌟实现思路 🌟具体实现 1.初始化数据图片 2.获取所需DOM元素 3.初始化页面 初始化缩略图 绑定事件 🌟完整代码 🌟写在最后 &…...

linux centos7 bash中字符串反向输出
给定一个字符串,如何反向(倒序)输出? 字符串反转的方法:a.对各个字符位置进行循环调换(从原字符串左边取出放在新字符串的右边;从原字符串右边取出放在新字符串的左边)。b.对各个字符由水平排列转为垂直排…...

git rebase和merge区别
一、概述 merge和rebase 标题上的两个命令:merge和rebase都是用来合并分支的。 这里不解释rebase命令,以及两个命令的原理,详细解释参考这里。 下面的内容主要说的是两者在实际操作中的区别。 1.1 什么是分支 分支就是便于多人在同一项目…...

Vue插槽实现商品列表-编辑渲染
商品列表 文章目录 商品列表核心步骤创建组件 1. MyTag组件详细步骤双击显示,自动聚焦失去焦点,隐藏输入框回显标签信息回车修修改内容,同时隐藏输入框 MyTable组件详细步骤1-动态的设置整个表格的数据 : props2-实现自定义结构-插…...

Vue开发之父子组件
创建父子组建,分三步。一是创建文件,二是引入组建,三是组件间通信。在components目录下新建sub文件夹,用于存放一下可以复用的子组件。比如新建一个SubCon.vue组件 <template><div class"first-app">{{ ms…...

fastadmin think-queue supervisor配置
起因是微信支付回调需要同时做发货处理,但是发货接口不能影响,需要队列进行异步处理1. 1.fastadmin 后台购买queue插件(基于think-queue消息队列) 2.代码 2.1 添加文件:application---->extra--->queue.php 内容:我这里用的数据库做…...
STM32 进不了main 函数
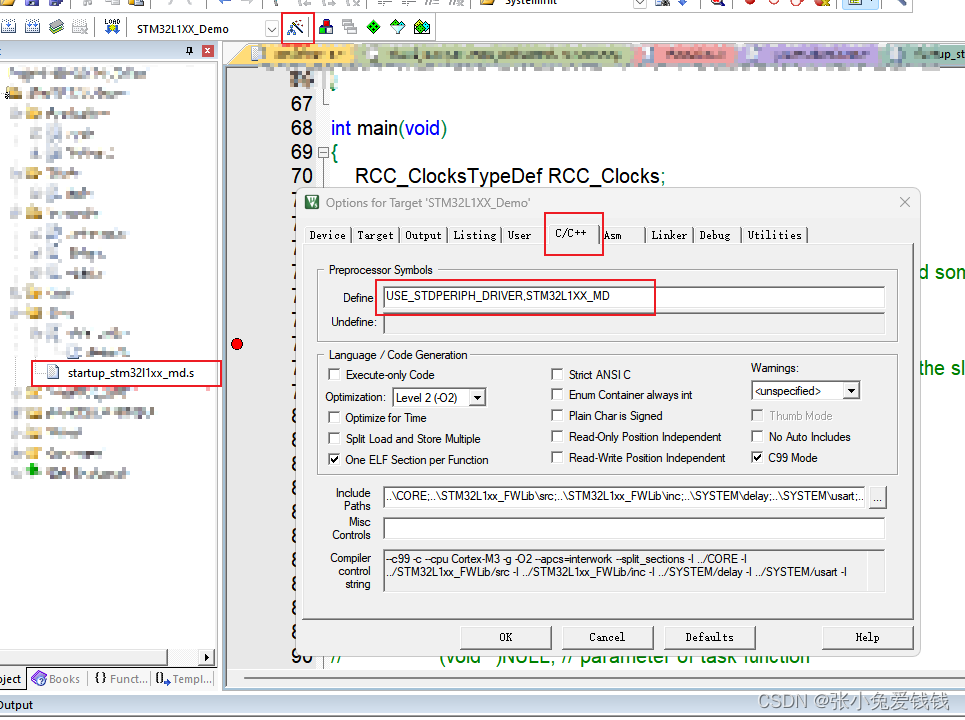
1. 我用的是STM32L151C8T6 的芯片,在github 上找了个别人的例程,拿来当模板改,由于他用的是HSE 外部晶振,我用的是内部晶振HSI,所以需要改系统时钟,改完后debug, 一直进不了main 函数࿰…...
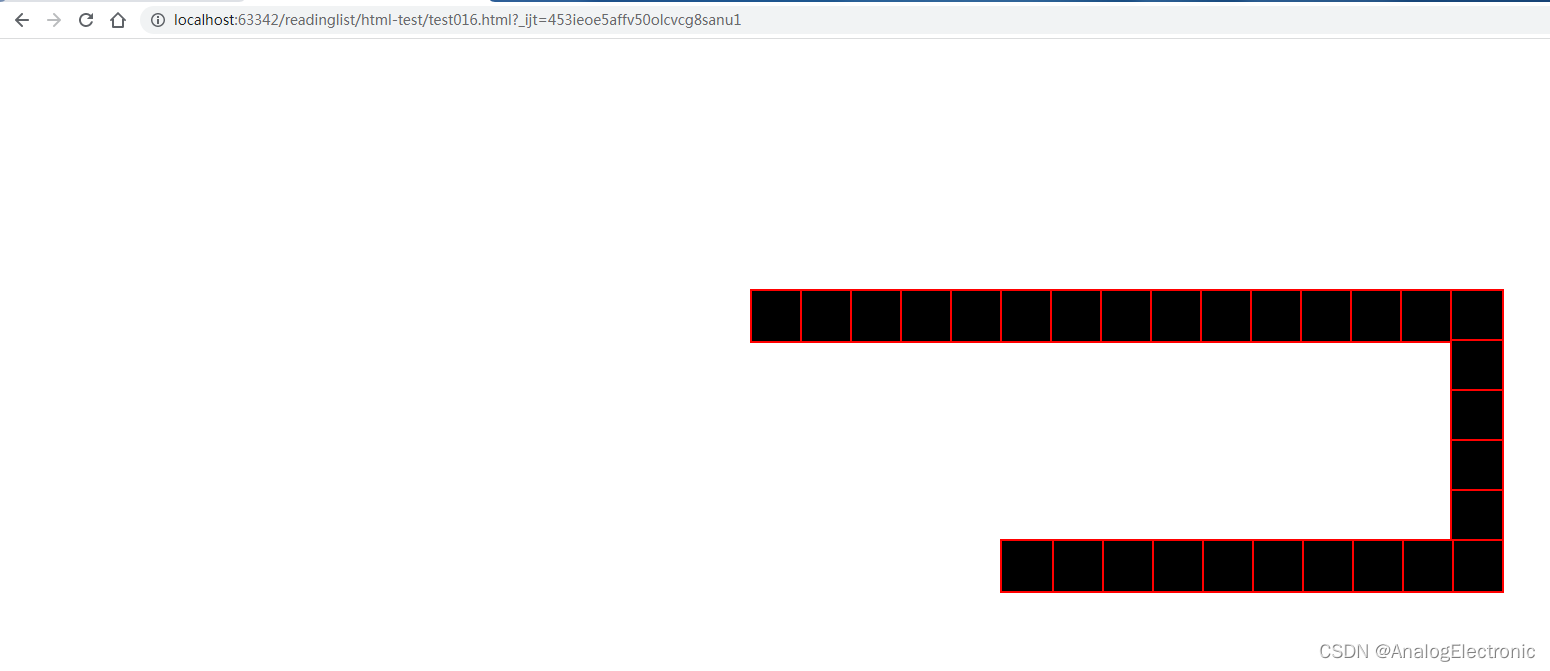
不用循环数组,js+html实现贪吃蛇
功能描述:每走10步随机改变一个方方向,当键盘按下方向键 w,s,a,d时,使用键盘方向控制蛇的移动,蛇头每撞到一次自身时改变屏幕颜色,蛇头碰到边界时从另一边回来。 实现思路:用个30大小的数组存放每个结点&a…...

什么是线程安全和线程不安全?
线程安全(Thread Safety)和线程不安全(Thread Unsafety)是与并发编程相关的概念,特别是在多线程环境中使用共享资源时会涉及到这些概念。 线程安全: 当多个线程同时访问共享资源时,如果在没有额外的同步措施的情况下,这些线程仍然能够正确地执行并保持数据的一致性,那…...
VUE笔记(十)Echarts
一、Echarts简介 1、什么是echarts ECharts是一款基个基于 JavaScript 的开源可视化图表库 官网地址:Apache ECharts 国内镜像:ISQQW.COM x ECharts 文档(国内同步镜像) - 配置项 示例:echarts图表集 2、第一个E…...
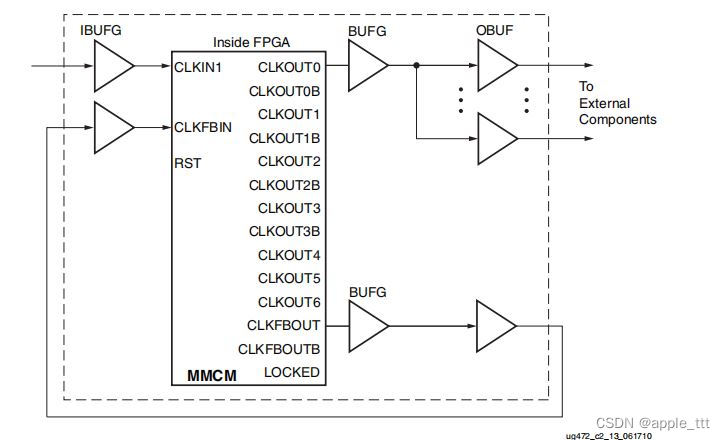
FPGA原理与结构——时钟IP核原理学习
一、前言 在之前的文章中,我们介绍了FPGA的时钟结构 FPGA原理与结构——时钟资源https://blog.csdn.net/apple_53311083/article/details/132307564?spm1001.2014.3001.5502 在本文中我们将学习xilinx系列的FPGA所提供的时钟IP核,来帮助我们进一…...
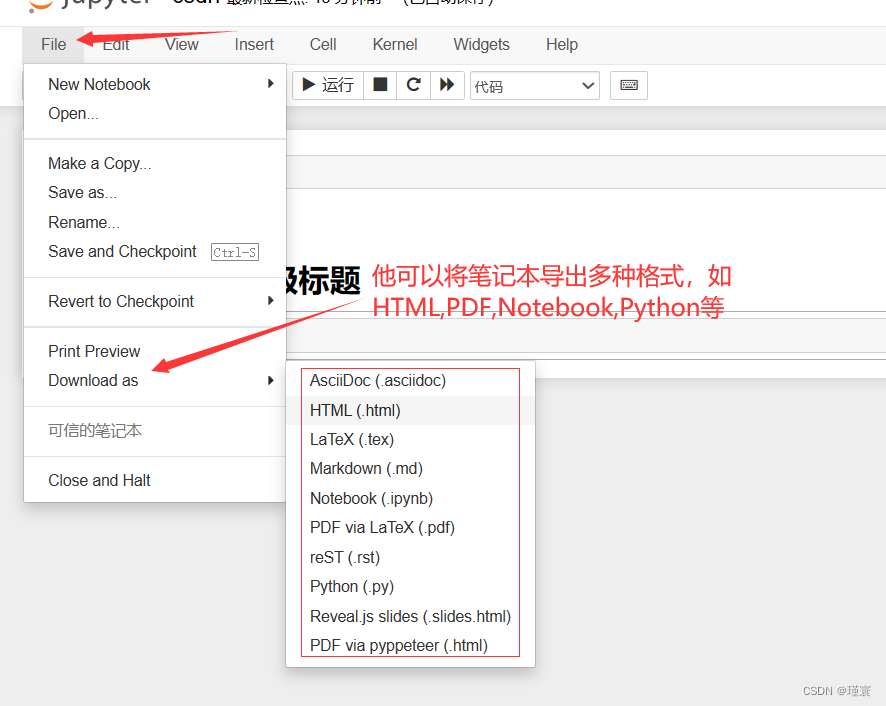
创建python环境——Anaconda
在Windows中安装Anaconda和简单使用 一.Anaconda发行概述 Anaconda是一个可以便捷获取和管理包,同时对环境进行统一管理的发行版本,它包含了conda、 Python在内的超过180个科学包及其依赖项。 1.Anaconda发行版本具有以下特点: (1)包含了…...

使用Linux部署Kafka教程
目录 一、部署Zookeeper 1 拉取Zookeeper镜像 2 运行Zookeeper 二、部署Kafka 1 拉取Kafka镜像 2 运行Kafka 三、验证是否部署成功 1 进入到kafka容器中 2 创建topic 生产者 3 生产者发送消息 4 消费者消费消息 四、搭建kafka管理平台 五、SpringBoot整合Kafka 1…...

pyechart笔记:opts.AxisOpts
定制化图表的轴线(x轴和y轴)的样式和设置 0 不设置坐标轴 c1(Bar().add_xaxis([力量,智力,敏捷]).add_yaxis(全能骑士,# 系列名称,用于 tooltip 的显示,legend 的图例筛选。[429,321,296],#系列数据).add_yaxis(猴子,[352,236,4…...

深度思考rpc框架面经之五:rpc熔断限流、rpc复用连接机制
11 RPC框架如何实现限流和熔断 推荐文章:RPC实现原理之核心技术-限流熔断 11.1 为什么Dubbo要做服务的限流?(根本原因是服务端进行自我保护) 限流是一种常见的系统保护手段。在分布式系统和微服务架构中,一个接口的过度使用可能会导致资源…...

Go 数组
数组用于在单个变量中存储相同类型的多个值,而不是为每个值声明单独的变量。 声明数组 在Go中,有两种声明数组的方式: 使用var关键字: 语法 var array_name [length]datatype{values} // 这里定义了长度 或者 var array_n…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...