【2023百度之星备赛】码蹄集 BD202301 公园(BFS求最短路)
题目
https://www.matiji.net/exam/brushquestion/1/4347/179CE77A7B772D15A8C00DD8198AAC74?from=1
题目大意:
给定一个无向图,有两个人往同一个目的地走,分别消耗体力TE、FE。如果他们到某个点汇合了,然后一起走向目的地,那么消耗的体力就会减少S。求他俩到景点 N 时,所需要的总消耗最少是多少?
思路
如下图所示,两个人F和T要先走到同一个汇合点x,然后在一起往目的地N点走。(图片来自【2023百度之星第一场题解】嘉宾:NOI、IOI金牌周航锐)
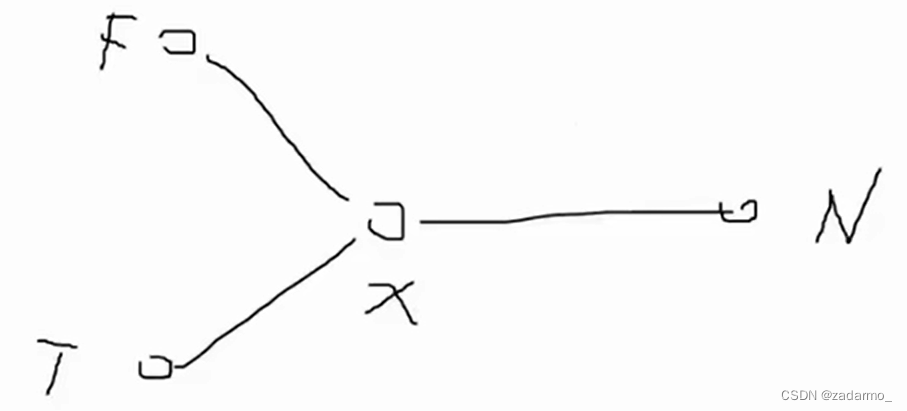
当汇合点x确定的时候,总体力 = F走到x的最短路径 * FE + T走到x的最短路径 * TE + x到N的最短路径 * (FE+TE-S)。由于无法确定哪个x是最优的汇合点,所以需要遍历所有的点,分别求出总体力,最后取一个最小值。
所以思路如下:
- 分别求F、T、N到所有点的最短距离
- 遍历所有点(汇合点),对于每个点,计算需要的总体力
- 取所有总体力的最小值
代码
#include<bits/stdc++.h> using namespace std;const int n = 40010;int TE, FE, S;
int T, F, N, M;vector<int> v[n]; // 邻接表
int d[3][n]; // 小度、度度熊、终点到每个点的最短距离void bfs(int dist[], int src) // 求src点到每个点的最短距离
{/* bfs求最短路的模板 */int q[n];for(int i = 1; i <= N; i ++ ) dist[i] = -1; // 初始化为-1,表示src不能到达iint hh = -1;int tt = 0;dist[src] = 0; q[++hh] = src;while (hh <= tt){int head = q[hh++];for (auto x : v[head]){if (dist[x] == -1){dist[x] = dist[head] + 1;q[++tt] = x;}}}
}int main( )
{cin >> TE >> FE >> S;cin >> T >> F >> N >> M;for(int i = 0; i < M; i ++ ) {int a, b;cin >> a >> b;v[a].push_back(b);v[b].push_back(a);}// 分别计算T、F、N到所有点的最短路径bfs(d[0], T);bfs(d[1], F);bfs(d[2], N);long long ans = 1e18;for (int i = 1; i <= N; i ++ ) {// 这里要判断是否等于-1。如果等于-1,说明当前汇合点i不能到达T、F、N中的某个点if (d[0][i] != -1 && d[1][i] != -1 && d[2][i] != -1){long long distance = 1ll * d[0][i] * TE + 1ll * d[1][i] * FE + 1ll * d[2][i] * (TE + FE - S);ans = min(ans, distance);}}if (ans == 1e18) cout << -1 << endl;else cout << ans << endl;return 0;
}
总结
BFS求解最短路径的代码:
const int N = 100010; // 题目所给的最大的点的个数
vector<int> v[N]; // 邻接表,用来存图void bfs(int dist[], int src)
{/* bfs求最短路的模板 */int q[N];// 初始化距离为-1,表示最开始src不能到达所有点for(int i = 1; i <= N; i ++ ) dist[i] = -1; // 将src入队,并将最短距离赋值为0int hh = -1;int tt = 0;dist[src] = 0; q[++hh] = src;// bfswhile (hh <= tt){// 取队首int head = q[hh++];// 遍历队首的邻接点for (auto x : v[head]){if (dist[x] == -1){dist[x] = dist[head] + 1;q[++tt] = x;}}}
}
相关文章:

【2023百度之星备赛】码蹄集 BD202301 公园(BFS求最短路)
题目 https://www.matiji.net/exam/brushquestion/1/4347/179CE77A7B772D15A8C00DD8198AAC74?from1 题目大意: 给定一个无向图,有两个人往同一个目的地走,分别消耗体力TE、FE。如果他们到某个点汇合了,然后一起走向目的地&…...
2022年下半年系统架构设计师真题(下午带答案)
试题一 (25分) 某电子商务公司拟升级其会员与促销管理系统,向用户提供个性化服务,提高用户的粘性。在项目立项之初,公司领导层一致认为本次升级的主要目标是提升会员管理方式的灵活性,由于当前用户规模不大,业务也相对…...
26、ADS瞬时波形仿真-TRANSIENT仿真(以共射放大器为例)
26、ADS瞬时波形仿真-TRANSIENT仿真(以共射放大器为例) 在本科期间,学习模电的时候总是要对各种三极管电路进行MULTISIM仿真,其实ADS具备相同的功能,而且对于射频电路,使用ADS进行仿真可以结合版图进行&am…...
【微服务部署】02-配置管理
文章目录 1.ConfigMap1.1 创建ConfigMap方式1.2 使用ConfigMap的方式1.3 ConfigMap使用要点建议 2 分布式配置中心解决方案2.1 什么时候选择配置中心2.2 Apollo配置中心系统的能力2.2.1 Apollo创建配置项目2.2.2 项目使用2.2.3 K8s中使用Apollo 1.ConfigMap ConfigMap是K8s提供…...

NTP时钟同步服务器
目录 一、什么是NTP? 二、计算机时间分类 三、NTP如何工作? 四、NTP时钟同步方式(linux) 五、时间同步实现软件(既是客户端软件也是服务端软件) 六、chrony时钟同步软件介绍 七、/etc/chrony.conf配置文件介…...
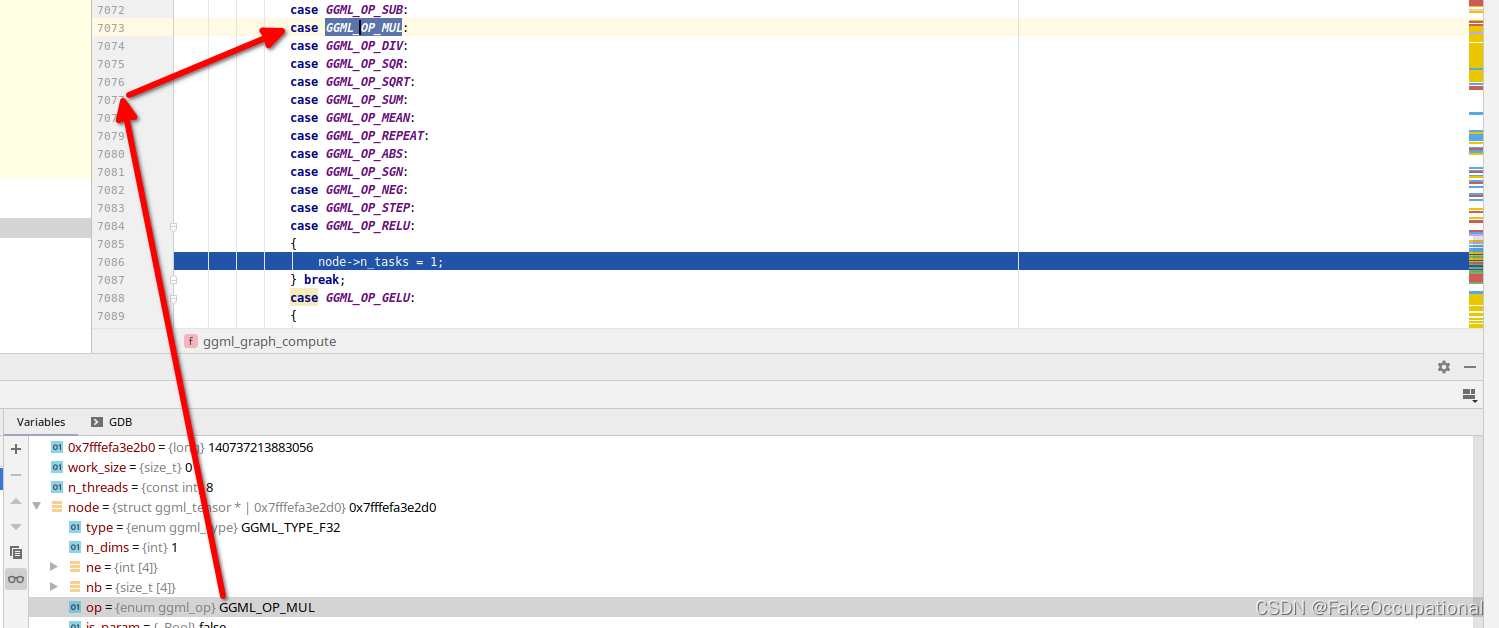
webassembly003 ggml GGML Tensor Library part-2 官方使用说明
https://github.com/ggerganov/whisper.cpp/tree/1.0.3 GGML Tensor Library 官方有一个函数使用说明,但是从初始版本就没修改过 : https://github1s.com/ggerganov/ggml/blob/master/include/ggml/ggml.h#L3-L173 This documentation is still a work in progres…...

ES主集群的优化参考点
因为流量比较大, 导致ES线程数飙高,cpu直往上窜,查询耗时增加,并传导给所有调用方,导致更大范围的延时。如何解决这个问题呢? ES负载不合理,热点问题严重。ES主集群一共有几十个节点࿰…...

全国范围内-二手房小区数据-2023-8月更新
收录融合去重多个平台数据:80万,仅供数字参考 数据纬度字段名注释枚举值基础信息id主键id:名称城市来源生成 md5值00001073838501125ec4473463ead9ccname名称瑞祥安文创园address地址(朝阳)双桥路东柳村口南口lng经度116.581903lat纬度39.89…...

第4章 循环变换
4.1 适配体系结构特征的关键技术 由于高级语言隐藏了底层硬件体系结构的大量细节,如果不经过优化直接将高级程序设计语言编写的程序部署在底层硬件上,往往无法充分利用底层硬件体系结构的处理能力。 算子融合不仅可以提…...

spring cloud使用git作为配置中心,git开启了双因子认证,如何写本地配置文件
问题 spring cloud使用git作为配置中心,git开启了双因子认证,死活认证不成功!!!!! 报错关键字 org.eclipse.jgit.api.errors.TransportException: https://git.qualink.com/zhaoxin15/sc-confi…...
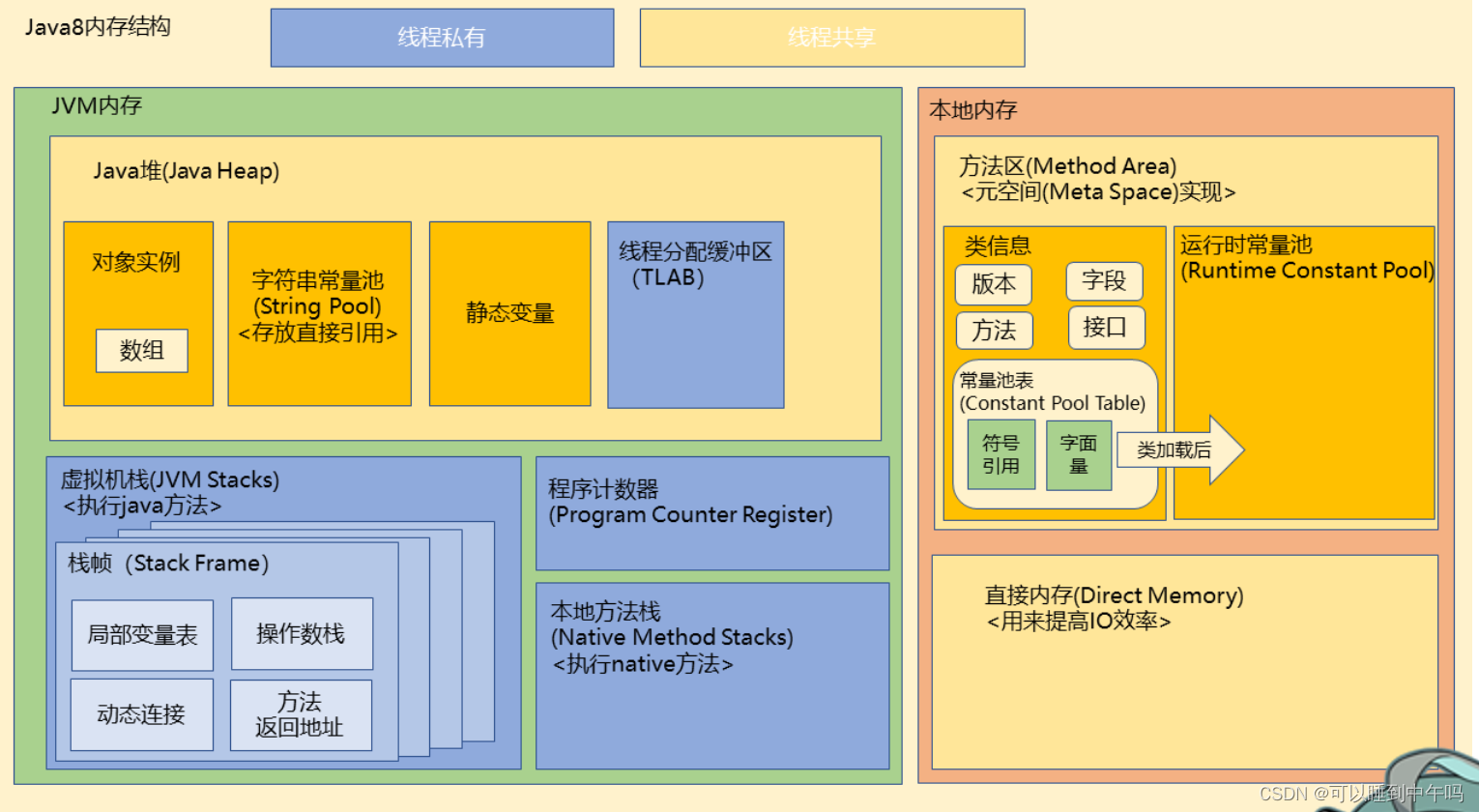
JVM内存管理、内存分区:堆、方法区、虚拟机栈、本地方法栈、程序计数器
内存管理 内存分区 线程共享 堆 存放实例,字符串常量(直接引用),静态变量,线程分配缓冲区(TLAB线程私有)。垃圾收集器管理的区域 方法区 非堆,和堆相对的概念。存储已被虚拟机加载的…...
 测试点全过)
L1-047 装睡(Python实现) 测试点全过
题目 你永远叫不醒一个装睡的人 —— 但是通过分析一个人的呼吸频率和脉搏,你可以发现谁在装睡!医生告诉我们,正常人睡眠时的呼吸频率是每分钟15-20次,脉搏是每分钟50-70次。下面给定一系列人的呼吸频率与脉搏,请你找…...
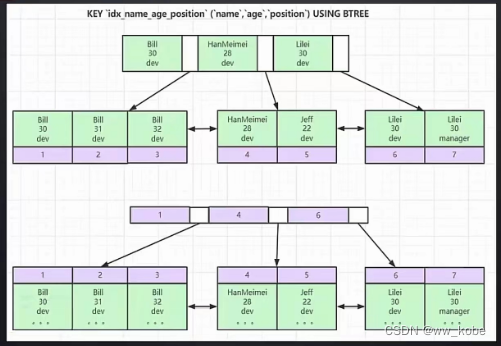
Mysql优化原理分析
一、存储引擎 1.1 MyISAM 一张表生成三个文件 xxx.frm:存储表结构xxx.MYD:存储表数据xxx.MYI:存储表索引 索引文件和数据文件是分离的(非聚集) select * from t where t.col1 30; 先去t.MYI文件查找30对应的索引…...

软考高级系统架构设计师系列案例考点专题一:软件架构设计
软考高级系统架构设计师系列案例考点专题一:软件架构设计 一、考点梳理及精讲1.质量属性判断与质量属性效用树2.必备概念3.架构风格对比4.MVC架构5.J2EE架构6.面向服务的架构SOA7.企业服务总线ESB一、考点梳理及精讲 系统架构设计师方面的知识在案例分析中每年必考1~2题,并且…...

css实现垂直上下布局的两种常用方法
例子:将两个<span>元素在<div>内垂直居中放置. 方法一:使用 Flexbox 来实现。 在下面的示例中,我将为 <div> 元素添加样式,使其成为一个 Flex 容器,并使用 Flexbox 属性将其中的两个 <span>…...
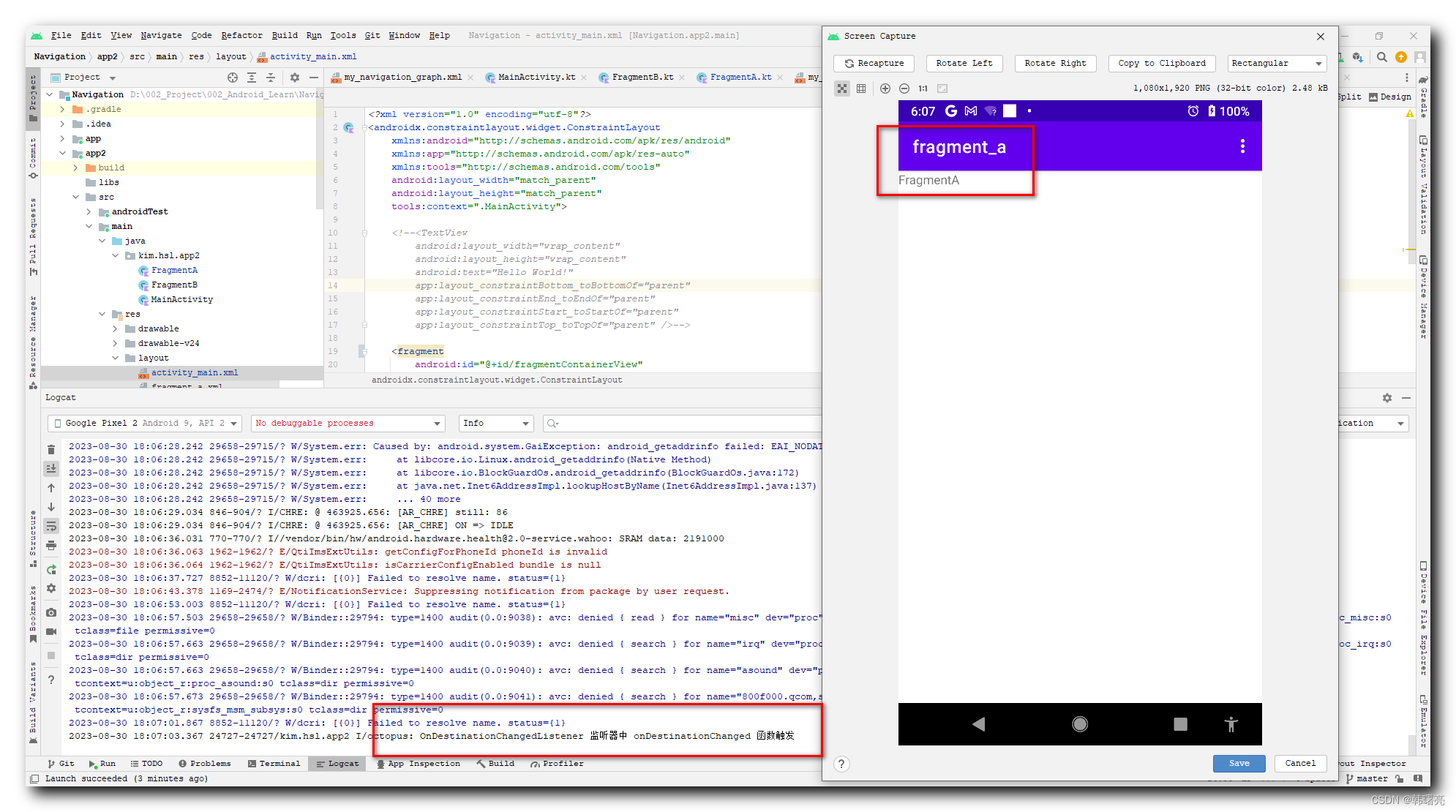
【Jetpack】Navigation 导航组件 ⑤ ( NavigationUI 类使用 )
文章目录 一、NavigationUI 类简介二、NavigationUI 类使用流程1、创建 Fragment2、创建 NavigationGraph3、Activity 导入 NavHostFragment4、创建菜单5、Activity 界面开发 NavigationUI 的主要逻辑 ( 重点 )a、添加 Fragment 布局b、处理 Navigation 导航逻辑 ( 重点 )c、启…...
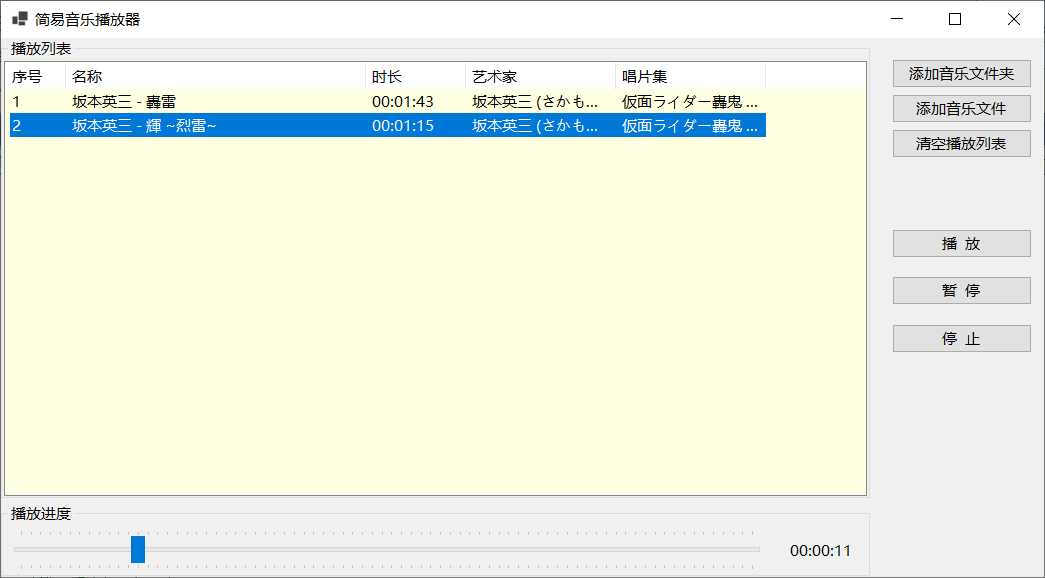
基于NAudio实现简单的音乐播放器
《测试.net开源音频库NAudio》介绍了使用NAudio实现音乐播放和录音的基本用法,本文基于NAudio的音乐播放功能实现简单的mp3音乐播放器程序,主要实现以下功能: 1)导入文件夹中的mp3音乐文件,直接导入多个mp3音乐文件…...

C++之“00000001“和“\x00\x00\x00\x01“用法区别(一百八十六)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 人生格言: 人生…...
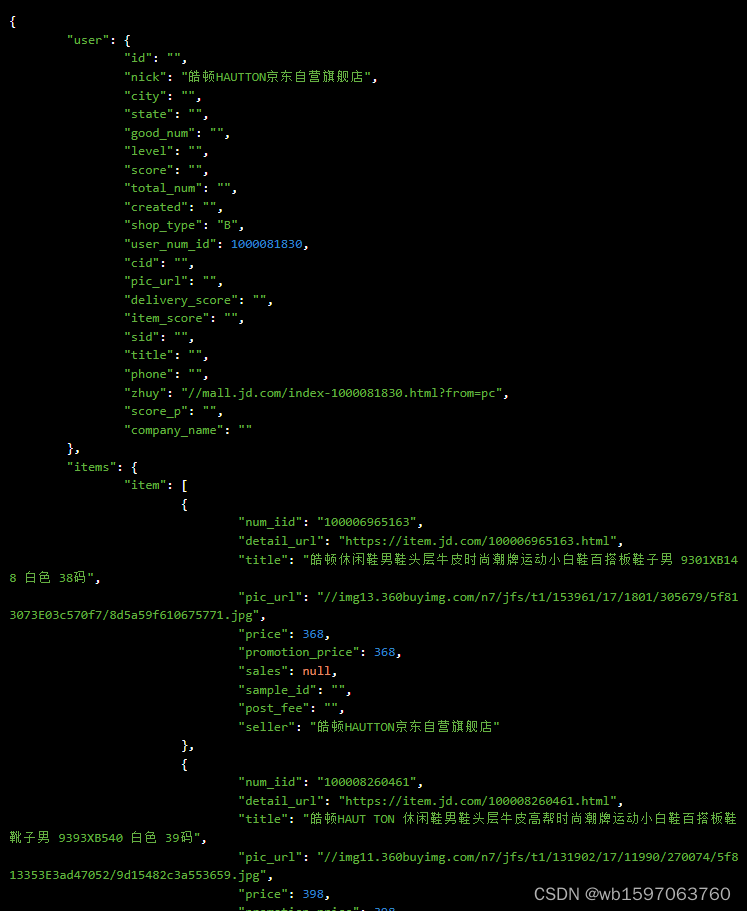
Java“魂牵”京东店铺所有商品数据接口,京东店铺所有商品API接口,京东API接口申请指南
要通过京东的API获取店铺所有商品数据,您可以使用京东开放平台提供的接口来实现。以下是一种使用Java编程语言实现的示例,展示如何通过京东开放平台API获取整店商品数据: 首先,确保您已注册成为京东开放平台的开发者,…...

vuex详细用法
Vuex是一个专门为Vue.js应用程序开发的状态管理模式。它可以帮助我们在Vue组件之间共享和管理数据,以及实现更好的代码组织和调试。 在Vue.js中,组件之间的数据通信可以通过props和事件来实现。然而,随着应用程序规模的增长,组件…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...
