如何使用Python和正则表达式处理XML表单数据

在日常的Web开发中,处理表单数据是一个常见的任务。而XML是一种常用的数据格式,用于在不同的系统之间传递和存储数据。本文通过阐述一个技术问题并给出解答的方式,介绍如何使用Python和正则表达式处理XML表单数据。我们将探讨整体设计、编写思路和一个完整的案例,以帮助读者理解和应用这项技术。
整体设计: 在处理XML数据表单时,我们需要考虑以下几个方面的设计:
- 设置代理信息:为了保证安全和隐私,我们需要设置代理信息来发送HTTP请求。将代理主机、端口、用户名和密码存储在相应的参数中。
- 发送HTTP请求并获取XML响应:使用Python的请求库发送HTTP请求,并获取XML响应。使用requests库发送GET请求,并设置代理信息。
- 解析XML数据:使用Python的内置库xml.etree.ElementTree来解析XML数据。使用xml.etree.ElementTree库解析XML响应,获取根元素。
- 使用正则表达式提取和处理数据:结合正则表达式,提取和处理XML表单数据中的信息。检索XML数据,使用正则表达式提取所需的信息,并进行相应的处理。
完整案例:以下是一个完整案例,演示如何使用Python和正则表达式处理XML表单数据:
Python复制
import ... requests
import ... xml.etree.ElementTree as ET
import re# 亿牛云爬虫代理参数设置
proxyHost = "u6205.5.tp.16yun.cn"
proxyPort = "5445"
proxyUser = "16QMSOML"
proxyPass = "280651"# 发送HTTP请求并获取XML响应
url = ... "http://example.com/form.xml"
proxies = {"http": f"http://{proxyUser}:{proxyPass}@{proxyHost}:{proxyPort}","https": f"http://{proxyUser}:{proxyPass}@{proxyHost}:{proxyPort}"
}
response = requests.get(url, ... proxies=proxies)# 解析XML数据
root = ET.fromstring(response.text)# 使用正则表达式提取和处理数据
phone_regex = r'\d{3}-\d{3}-\d{4}'
for field in root.iter('field'):name = field.attrib['name']value = field.textif name == 'phone':match = re.search(phone_regex, value)if match:phone_number = match.group()break# 打印提取的电话号码
print(f"Phone number: {phone_number}")
根据上述内容,使用Python和正则表达式在日常工作中处理XML表单数据具有重要性。它可以帮助我们提取和处理数据,清洗和验证数据,实现数据转换和集成,提升工作效率,以及处理错误掌握这些技能可以使我们更加、准确地高效处理XML表单数据,从而提升工作质量和效率。
相关文章:

如何使用Python和正则表达式处理XML表单数据
在日常的Web开发中,处理表单数据是一个常见的任务。而XML是一种常用的数据格式,用于在不同的系统之间传递和存储数据。本文通过阐述一个技术问题并给出解答的方式,介绍如何使用Python和正则表达式处理XML表单数据。我们将探讨整体设计、编写思…...

LA@方阵相似@相似矩阵的性质
文章目录 相似矩阵引言相似矩阵定义相似变换相似变换矩阵相似矩阵的矩阵多项式和特征值相同推论:与对角阵相似的矩阵性质定理 相似矩阵性质相似矩阵的乘方性质相似矩阵和矩阵多项式相似对角阵 对角阵多项式的展开小结 相似矩阵 引言 对角阵是矩阵中最简单的一类矩阵 对角阵相…...
ZLMediaKit 各种推拉流
1 用ffmpeg 推音视频流 ./ffmpeg -f dshow -i video"HP Wide Vision HD Camera" -f dshow -i audio"麦克风阵列 (Realtek High Definition Audio)" -rtbufsize 100M -max_delay 100 -pix_fmt yuv420p -tune zerolatency -c:v libx264 -crf 18 -s 1280x720…...
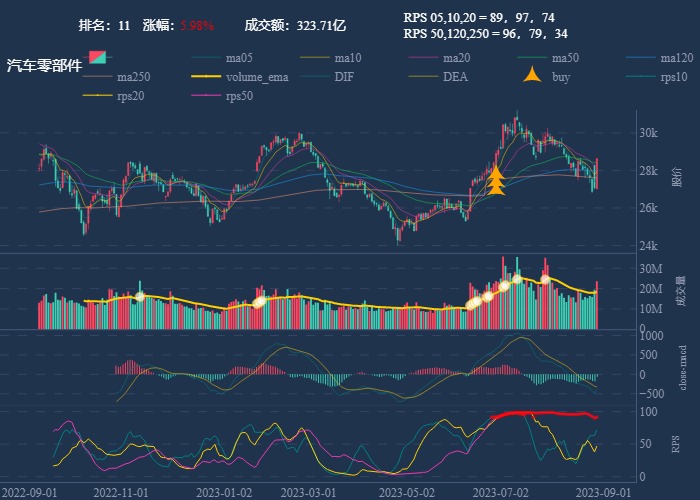
行业追踪,2023-08-29
自动复盘 2023-08-29 凡所有相,皆是虚妄。若见诸相非相,即见如来。 k 线图是最好的老师,每天持续发布板块的rps排名,追踪板块,板块来开仓,板块去清仓,丢弃自以为是的想法,板块去留让…...

【简单】228. 汇总区间
原题链接:https://leetcode.cn/problems/summary-ranges/description/ 228. 汇总区间 给定一个 无重复元素 的 有序 整数数组 nums 。 返回 恰好覆盖数组中所有数字 的 最小有序 区间范围列表 。也就是说,nums 的每个元素都恰好被某个区间范围所覆盖&…...
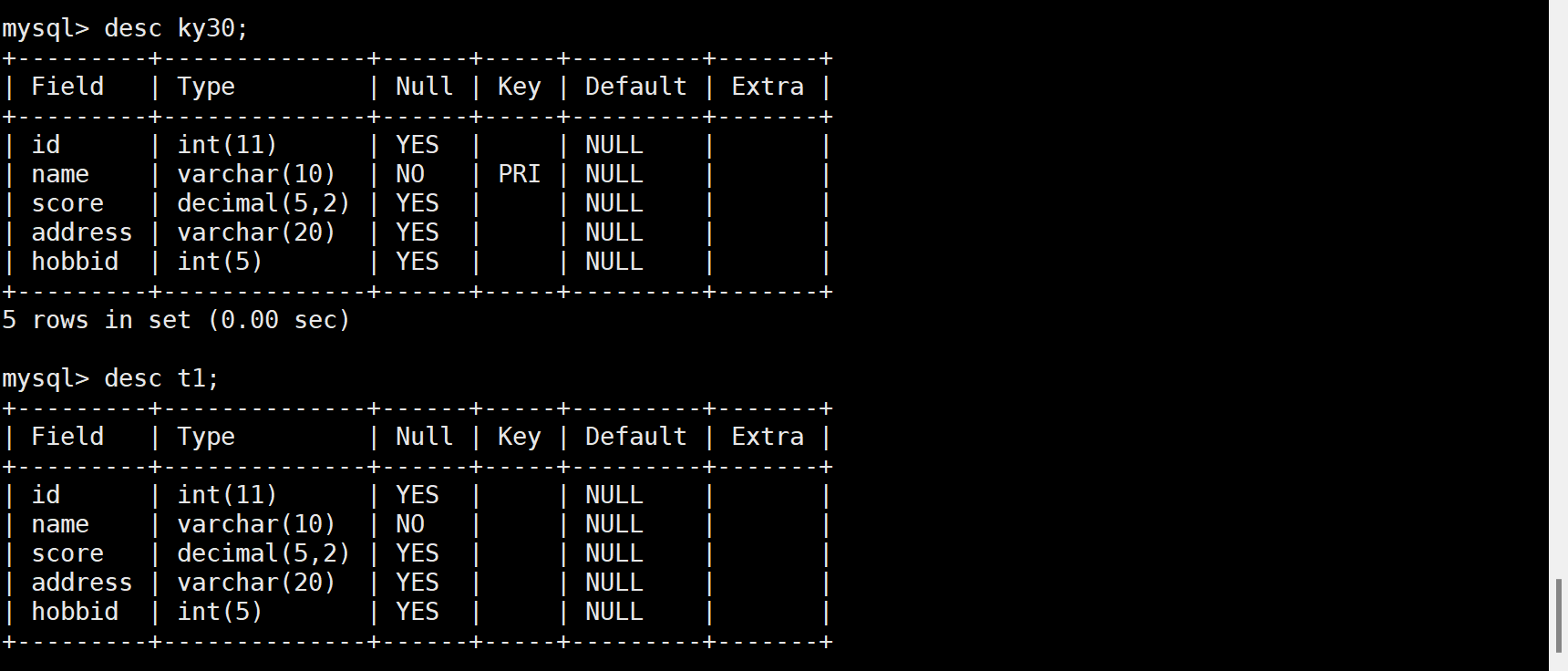
Mysql高级语句
高级语句 1.按关键字排序 SELECT column1, column2, ... FROM table_name ORDER BY column1, column2, ... ASC|DESC ASC 是按照升序进行排序的,是默认的排序方式,即 ASC 可以省略。 SELECT 语句中如果没有指定具体的排序方式,则默认按 ASC…...

Python中 re.compile 函数的使用
前言 嗨喽,大家好呀~这里是爱看美女的茜茜呐 以下介绍在python的re模块中怎样应用正则表达式 👇 👇 👇 更多精彩机密、教程,尽在下方,赶紧点击了解吧~ python源码、视频教程、插件安装教程、资料我都准备…...
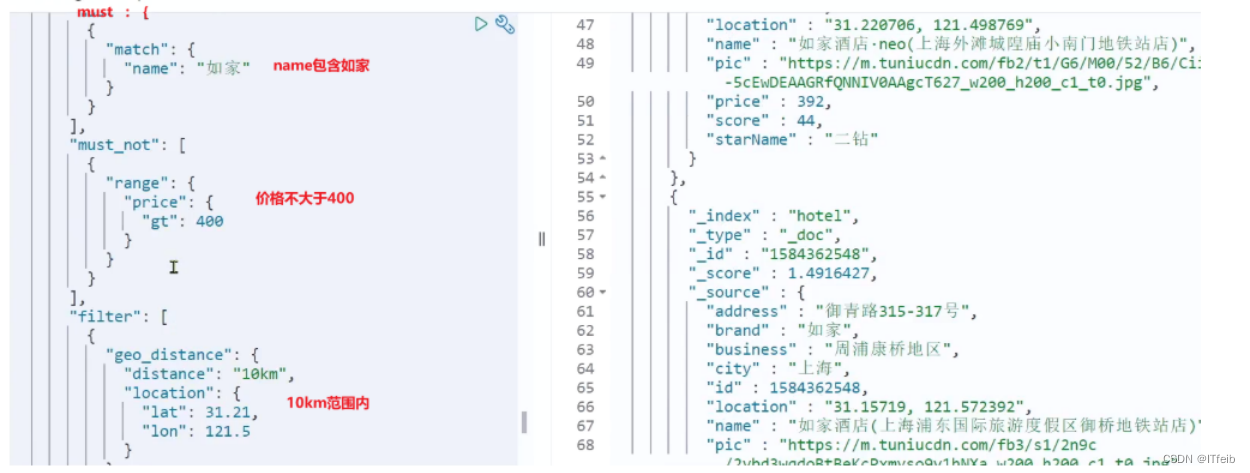
【分布式搜索引擎es】
文章目录 数据搜索DSL实现查询文档搜索结果处理 RestClient实现 elasticsearch最擅长的是 搜索和 数据分析。 数据搜索 DSL实现 查询文档 常见的查询类型包括: 查询所有:查询出所有数据,一般测试用。例如:match_all全文检索…...

单片机的ADC
如何理解ADC。ADC就是将模拟量转换成数字量的过程,就是转换为计算机所能存储的0和1序列,比如将模拟量转换为一个字节,所以这个字节的大小要能反应模拟量的大小,比如一个0-5V的电压测量量(外部输入电压最小0V,最大为5V&…...
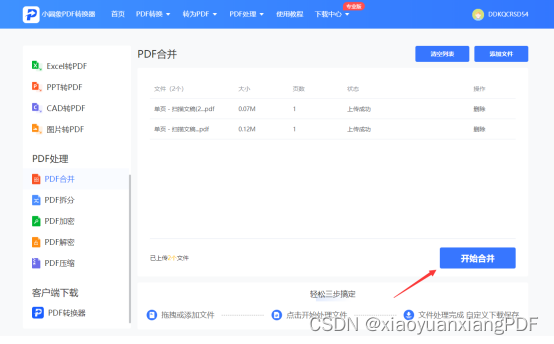
如何把pdf文件合并?分享最新pdf合并方法
在所有文档格式中,pdf应该是最常用的,像产品介绍、商务合同、法律文书等等,这些都是pdf格式的。有时候出于工作需要,我们要把两份或者多份pdf文件合并在一起,那么问题来了,如何把pdf文件合并呢?小编最近发…...
)
笙默考试管理系统-MyExamTest----codemirror(11)
笙默考试管理系统-MyExamTest----codemirror(11) 目录 笙默考试管理系统-MyExamTest----codemirror(11) 一、 笙默考试管理系统-MyExamTest----codemirror 二、 笙默考试管理系统-MyExamTest----codemirror 三、 笙默考试管…...
Spring MVC 五 - Spring MVC的配置和DispatcherServlet初始化过程
今天的内容是SpringMVC的初始化过程,其实也就是DispatcherServilet的初始化过程。 Special Bean Types DispatcherServlet委托如下一些特殊的bean来处理请求、并渲染正确的返回。这些特殊的bean是Spring MVC框架管理的bean、按照Spring框架的约定处理相关请求&…...
Ramp 有点意思的题目
粗一看都不知道这个要干什么,这 B 装得不错。 IyEvdXNyL2Jpbi9lbnYgcHl0aG9uMwoKJycnCktlZXAgdXMgb3V0IG9mIGdvb2dsZSBzZWFyY2ggcmVzdWx0cy4uCgokIG9kIC1kIC9kZXYvdXJhbmRvbSB8IGhlYWQKMDAwMDAwMCAgICAgNjAyMTUgICAyODc3OCAgIDI5MjI3ICAgMjg1NDggICA2MjY4NiAgIDQ1MT…...
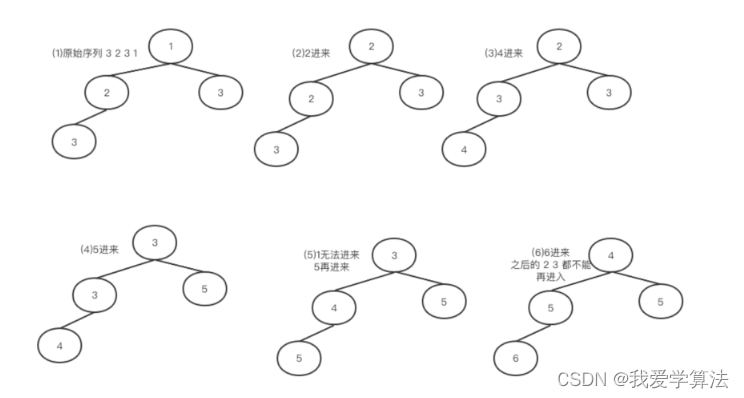
算法通关村14关 | 堆在数组中找第k大的元素应用
1. 在数组中找第k大元素 题目 LeetCode215:给定整数数组nums和整数k,请返回数组中第k个最大的元素, 思路 解题思路用三个,选择法,堆查找和快速排序。 我们选择用大堆小堆解决问题,“找最大用小堆ÿ…...
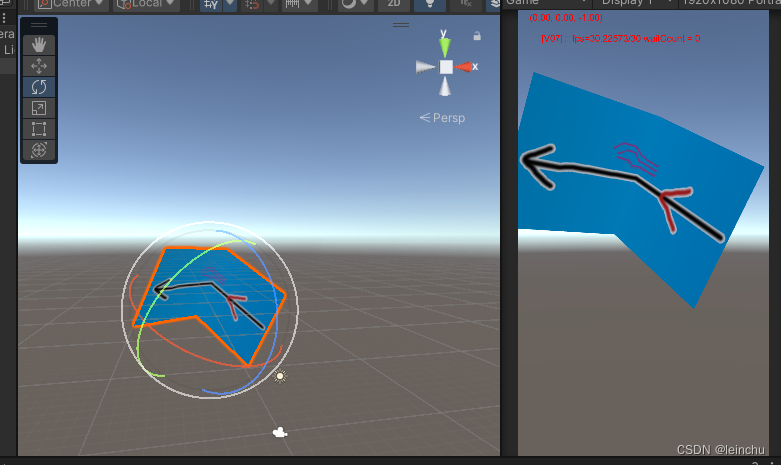
Unity 顶点vertices,uv,与图片贴图,与mesh
mesh就是组成3d物体的三角形们。 mesh由顶点组成的三角形组成,三角形的大小 并不 需要一样,由顶点之间的位置决定。 mesh可以是一个或者多个面。 贴图的原点在左下角,uv是贴图的坐标,数量和顶点数一样(不是100%确定…...

Shell编程之函数
目录 基本概念 自定义函数 系统函数 1.read 2.basename 3.dirname 基本概念 将一段代码组合封装在一起实现某个特定的功能或返回某个特定的值,然后给这段代码取个名字,也就是函数名,在需要实现某个特定功能的时候直接调用函数名即可。 函…...

10.物联网LWIP之TCP状态转变
一。TCP状态机 1.青粗线:理想TCP状态转变(服务器视角下) 2.虚线:被动TCP状态转变(服务器视角下) 3.细实线:不经常出现的TCP状态转变(类似于边界处理) 1.青粗线解释--》服…...

Img标签的src地址自动拼接本地域名(localhost:8080)导致图片不显示问题
摘要:做Vueelement ui项目的时候,发现使用element ui的upload上传图片时,不显示的问题。我项目的图片是上传到七牛云,长传成功后返回存储在七牛云中的地址。后面发现是因为返回的地址是外部地址,需要完整的URL…...

数据结构入门 — 栈
本文属于数据结构专栏文章,适合数据结构入门者学习,涵盖数据结构基础的知识和内容体系,文章在介绍数据结构时会配合上动图演示,方便初学者在学习数据结构时理解和学习,了解数据结构系列专栏点击下方链接。 博客主页&am…...
Unity Android 之 在Unity 中引入 OkHttp的操作注意(OKHttp4.xx- kotlin 的包)简单记录
Unity Android 之 在Unity 中引入 OkHttp的操作注意(OKHttp4.xx- kotlin 的包)简单记录 目录 Unity Android 之 在Unity 中引入 OkHttp的操作注意(OKHttp4.xx- kotlin 的包)简单记录 一、简单介绍 二、OKHttp 4.xx 的 SDK 封装 aar 给 Unity 的使用注意 三、附录 OKHttp 的…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

在 Spring Boot 中使用 JSP
jsp? 好多年没用了。重新整一下 还费了点时间,记录一下。 项目结构: pom: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://ww…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...

全面解析数据库:从基础概念到前沿应用
在数字化时代,数据已成为企业和社会发展的核心资产,而数据库作为存储、管理和处理数据的关键工具,在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理,到社交网络的用户数据存储,再到金融行业的交易记录处理&a…...

STM32标准库-ADC数模转换器
文章目录 一、ADC1.1简介1. 2逐次逼近型ADC1.3ADC框图1.4ADC基本结构1.4.1 信号 “上车点”:输入模块(GPIO、温度、V_REFINT)1.4.2 信号 “调度站”:多路开关1.4.3 信号 “加工厂”:ADC 转换器(规则组 注入…...

鸿蒙Navigation路由导航-基本使用介绍
1. Navigation介绍 Navigation组件是路由导航的根视图容器,一般作为Page页面的根容器使用,其内部默认包含了标题栏、内容区和工具栏,其中内容区默认首页显示导航内容(Navigation的子组件)或非首页显示(Nav…...

【R语言编程——数据调用】
这里写自定义目录标题 可用库及数据集外部数据导入方法查看数据集信息 在R语言中,有多个库支持调用内置数据集或外部数据,包括studentdata等教学或示例数据集。以下是常见的库和方法: 可用库及数据集 openintro库 该库包含多个教学数据集&a…...
