在iPhone 15发布之前,iPhone在智能手机出货量上占据主导地位,这对安卓来说是个坏消息
可以说这是一记重拳,但似乎没有一个有价值的竞争者能与苹果今年迄今为止的智能手机出货量相媲美。
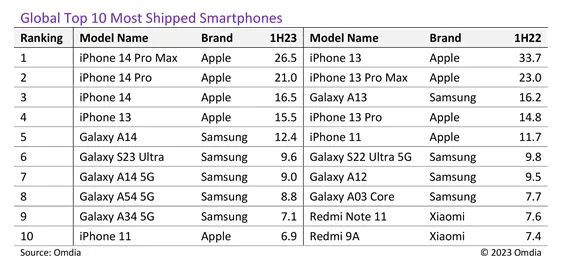
事实上,根据Omdia智能手机型号市场跟踪机构收集的数据,苹果的iPhone占据了前四名。位居榜首的是iPhone 14 Pro Max,2023年上半年出货量约为2650万部,成为出货量最大的智能手机。

更令人惊讶的是,苹果占据了榜单的前四位。这些估计对该公司即将于9月12日发布的iPhone 15来说是个好兆头。考虑到今年这批iPhone的兴奋和热议,有传言称它们将提供多年来最大的升级,看看2023年下半年会发生什么将是一件有趣的事情。
苹果在榜单上占据主导地位,并轻松击退了安卓领域最激烈的竞争对手。考虑到去年同一名单上有更多的安卓手机,这本身就令人震惊。在我们即将进入关键的假期之际,所有这些都可能给苹果带来更大的蛋糕。
一、iPhone 15的好消息
这份榜单还强调了一个事实,即消费者不怕花钱买苹果的智能手机,因为iPhone 14 Pro和iPhone 14是榜单前三名。我们可能会看到最昂贵的即将推出的机型iPhone 15 Pro和iPhone 15 Pro Max/iPhone 15 Ultra的销量会更强劲,据传它们的价格都更高。
特别是iPhone 15 Pro Max/iPhone 15 Ultra,据传起价1299美元,因为它有望获得所有独家功能和升级,比如耐用的钛框架、潜望镜长焦相机、A17仿生芯片等等。与此同时,iPhone 15 Pro也有望提价100美元,使其起价达到1100美元。
如果这份报告有任何迹象的话,苹果在今年下半年的出货量可能会更强劲。考虑到通货膨胀对消费者支出的影响,这是一个发人深省的提醒,人们仍然愿意花钱给自己买最好的手机。虽然从技术上讲,出货量并不能转化为销售额,但它仍然是市场需求的一个指标。

二、三星是唯一上榜的安卓系统制造商
不幸的是,对于该领域的其他人来说,这是一件单方面的事情,只有三星是唯一一家上榜的手机制造商。这与去年同期的两款Redmi手机成功上榜形成了鲜明对比。
令人震惊的是,三星Galaxy A13荣登韩国智能手机制造商排行榜榜首。这款廉价手机的全球出货量达1240万部,实际上超过了Galaxy S23 Ultra的960万部。三星的其他设备包括Galaxy A14 5G、Galaxy A54 5G和Galaxy A34 5G。

三、Pixel手机明显缺席
你可能会认为谷歌的Pixel手机会以某种方式上榜,但它们在报告中明显缺席。考虑到谷歌在智能手机定价方面的积极性,这在某种程度上令人难以置信。
例如,谷歌Pixel 7a是一款中等规格的手机,售价499美元,是最便宜的手机之一。除此之外,其旗舰手机Pixel 7和Pixel 7 Pro比同类手机低100美元,从而削弱了直接竞争对手的竞争力。你可能会认为这种激进的降价足以刺激其手机的出货量,但事实并非如此。

这一切都给其即将推出的Pixel 8手机带来了更大的压力,使其能够脱颖而出。考虑到苹果希望通过iOS 17的预期发布和iPhone 15的发布来抢尽风头,安卓制造商需要做出相应的回应,这样苹果就不会在假期成为t台。
相关文章:

在iPhone 15发布之前,iPhone在智能手机出货量上占据主导地位,这对安卓来说是个坏消息
可以说这是一记重拳,但似乎没有一个有价值的竞争者能与苹果今年迄今为止的智能手机出货量相媲美。 事实上,根据Omdia智能手机型号市场跟踪机构收集的数据,苹果的iPhone占据了前四名。位居榜首的是iPhone 14 Pro Max,2023年上半年…...

题目:2620.计数器
题目来源: leetcode题目,网址:2620. 计数器 - 力扣(LeetCode) 解题思路: 定义两个全局变量,一个判断 n 是否改变,另一个记录上一次出现的数。 解题代码: /*** par…...
列表(SHOW VARIABLES 的结果例))
【MySQL】MySQL系统变量(system variables)列表(SHOW VARIABLES 的结果例)
文章目录 【MySQL】MySQL系统变量(system variables)列表(SHOW VARIABLES 的结果例)SHOW VARIABLES 的结果例参考 【免责声明】文章仅供学习交流,观点代表个人,与任何公司无关。 编辑|SQL和数据库技术(ID:S…...

【多AZ】浅述云计算多az
多AZ(Availability Zone)是云计算中一种重要的容灾和冗余策略,它通过在不同的地理位置或不同的设备上存储数据副本以及网络切换策略,以保证在单个设备或地理位置发生故障时,云加计算集群仍然能够提供服务。 多AZ的特点…...

Element浅尝辄止13:Collapse 折叠面板
通过折叠面板收纳内容区域 1.如何使用? 可同时展开多个面板,面板之间不影响 <el-collapse v-model"activeNames" change"handleChange"><el-collapse-item title"一致性 Consistency" name"1">&l…...

51 单片机包含头文件 BIN51.H 直接写二进制数字
51 单片机包含头文件 BIN51.H 直接写二进制 最近学习 51 单片机,写代码的时候感觉用二进制的形式更直观。就是每次都需要宏定义,太麻烦。干脆把所有的8位二进制数字全部用宏定义写出来,放进头文件,下次使用直接包含头文件就行。 …...
php环境搭建步骤(与资源配套使用版)
1.将phpEnv.zip下载到D盘下 2.解压到当前文件夹 3.找到Apache24下的bin目录,执行cmd操作,回车。 4.在cmd中执行代码 Httpd -k install -n “Apache24” 4.使用winR键打开运行,输入services.msc ,回车,进入服务 …...

java 集合处理:
// 1 数组转map public static void main(String[] args) {String backendIdStr"[\"backend-mvj05upv7yc\",\"backend-mvj055qvric\",\"backend-mvj04hlutx4\"]";String[] backendIdList JsonUtil.asObject(backendIdStr, String[].c…...

算法训练第五十二天
718. 最长重复子数组 - 力扣(LeetCode) class Solution { public:int findLength(vector<int>& nums1, vector<int>& nums2) {vector<vector<int>> dp(nums1.size() 1,vector<int>(nums2.size() 1,0));int res…...

LeetCode——回溯篇(三)
刷题顺序及思路来源于代码随想录,网站地址:https://programmercarl.com 目录 46. 全排列 47. 全排列 II 332. 重新安排行程 51. N 皇后 37. 解数独 46. 全排列 给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任…...

Python爬取京东商品评论
寻找数据真实接口 打开京东商品网址查看商品评价。我们点击评论翻页,发现网址未发生变化,说明该网页是动态网页。 API名称:item_review-获得JD商品评论 公共参数 获取API测试key&secret 名称类型必须描述keyString是调用keyÿ…...
ROS机器人编程---------(一)安装ROS
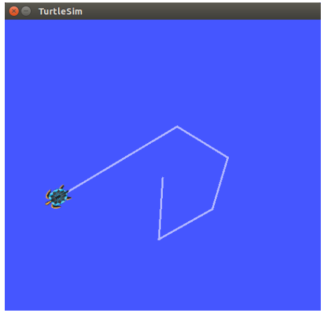
安装ROS 打开终端按顺序执行下面命令 默认安装在/opt/ros路径下 打开一个终端输入roscore 测试是否安装成功 启动ROS Master roscore启动小海龟仿真器 rosrun turtlesim turtlesim_node启动海龟控制结点 rosrun turtlesim turtlesim_teleop_key使用键盘方向键控…...

Maven入门教程(一):安装Maven环境
视频教程:Maven保姆级教程 Maven入门教程(一):安装Maven环境 Maven入门教程(二):idea/Eclipse使用Maven Maven入门教程(三):Maven语法 Maven入门教程(四):Nexus私服 Maven入门教程(五):自定义脚手架 Maven项…...

CSS中可继承与不可继承属性
可继承 1. 字体属性: font、font-style、font-variant、font-weight、font-size、line-height等属性是字体样式的属性,都可以被子元素继承。 2. 文本属性: color、text-indent、text-align、text-decoration、text-transform、letter-spa…...
Vscode画流程图
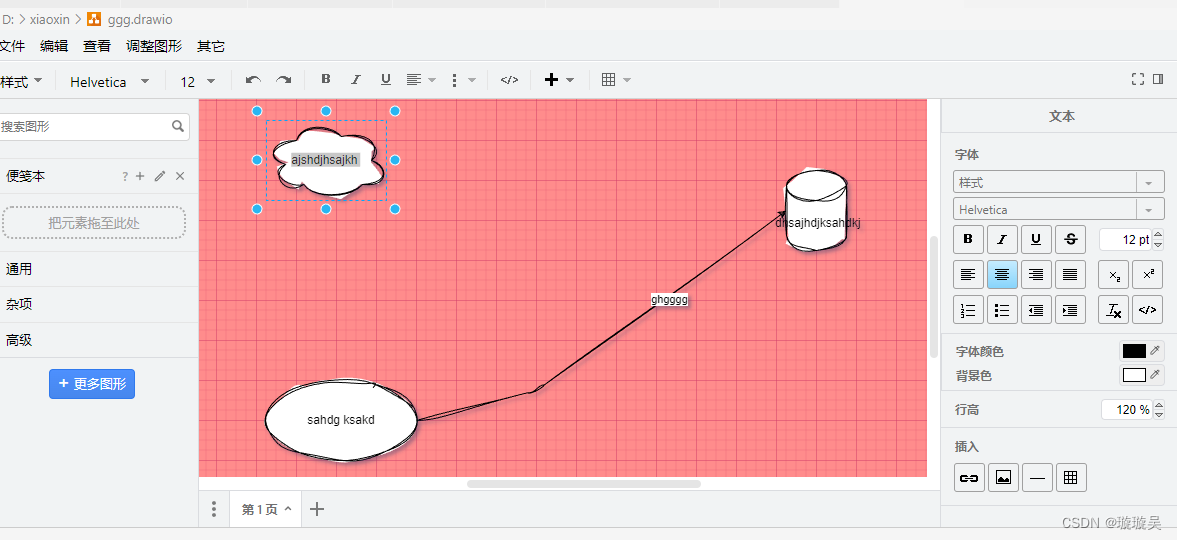
1.下载插件 Draw.id Integration 2.桌面新建文件,后缀名改为XXX.drawio 在vscode打开此文件 ,就可以进行绘制流程图啦...

【K8S系列】深入解析k8s网络插件—Cilium
序言 做一件事并不难,难的是在于坚持。坚持一下也不难,难的是坚持到底。 文章标记颜色说明: 黄色:重要标题红色:用来标记结论绿色:用来标记论点蓝色:用来标记论点 在现代容器化应用程序的世界中…...

OpenCV(十六):高斯图像金字塔
目录 1.高斯图像金字塔原理 2.高斯图像金字塔实现 1.高斯图像金字塔原理 高斯图像金字塔是一种用于多尺度图像表示和处理的重要技术。它通过对图像进行多次高斯模糊和下采样操作来生成不同分辨率的图像层级,每个层级都是原始图像的模糊和降采样版本。 以下是高斯…...
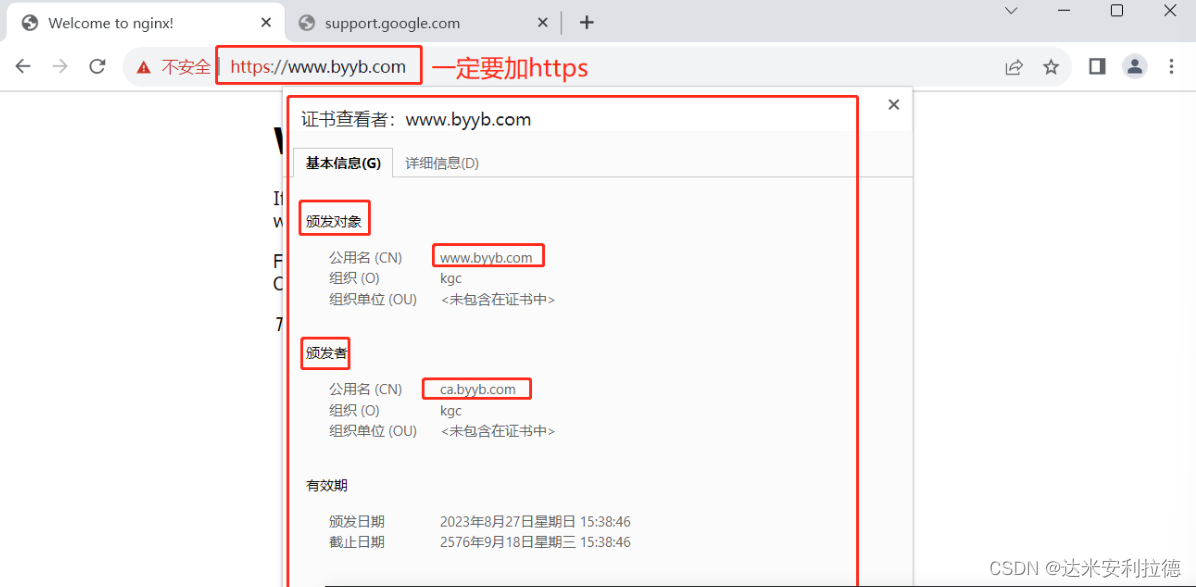
Nginx配置及优化3
Nginx配置及优化3 一、网页状态页二、nginx第三方模块2.1、echo模块 三、变量3.1、内置变量3.1.1、常用的内置变量3.1.2、举个例子 3.2、自定义变量 四、自定义访问日志优化4.1、自定义访问日志的格式4.2、自定义json格式日志 五、nginx压缩功能六、HTTPS功能6.1、nginx的HTTPS…...

网络直播源码UDP协议搭建:为平台注入一份力量
网络直播源码中的UDP协议的定义: UDP协议又名用户数据报协议,是一种轻量级、无连接的协议。在网络直播源码平台中,UDP协议有着高速传输与实时性的能力,尤其是在网络直播源码实时性要求较高的场景,UDP协议的应用有着重要…...

Ubuntu/linux系统环境变量配置详解
一 环境变量配置文件解释 /etc/profile 在登录时,操作系统定制用户环境时使用的第一个文件 ,此文件为系统的每个用户设置环境信息,当用户第一次登录时,该文件被执行。 /etc /environment 在登录时操作系统使用的第二个文件, 系统在读取你自己的profile前,设置环境文件的环境变…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...

Linux部署私有文件管理系统MinIO
最近需要用到一个文件管理服务,但是又不想花钱,所以就想着自己搭建一个,刚好我们用的一个开源框架已经集成了MinIO,所以就选了这个 我这边对文件服务性能要求不是太高,单机版就可以 安装非常简单,几个命令就…...

Axure 下拉框联动
实现选省、选完省之后选对应省份下的市区...

在golang中如何将已安装的依赖降级处理,比如:将 go-ansible/v2@v2.2.0 更换为 go-ansible/@v1.1.7
在 Go 项目中降级 go-ansible 从 v2.2.0 到 v1.1.7 具体步骤: 第一步: 修改 go.mod 文件 // 原 v2 版本声明 require github.com/apenella/go-ansible/v2 v2.2.0 替换为: // 改为 v…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...
