【图解算法数据结构】分治算法篇 + Java代码实现
文章目录
- 一、重建二叉树
- 二、数值的整数次方
- 三、打印从 1 到最大的 n 位数
- 四、二叉搜索树的后序遍历序列
- 五、数组中的逆序对
一、重建二叉树

public class Solution {int[] preorder;HashMap<Integer, Integer> dic = new HashMap<>();public TreeNode buildTree(int[] preorder, int[] inorder) {this.preorder = preorder;for (int i = 0; i < inorder.length; i++) {dic.put(inorder[i], i);}return recur(0, 0, inorder.length - 1);}TreeNode recur(int root, int left, int right) {if (left > right) {// 递归终止return null;}// 建立根节点TreeNode node = new TreeNode(preorder[root]);// 划分根节点、左子树、右子树int i = dic.get(preorder[root]);// 开启左子树递归node.left = recur(root + 1, left, i - 1);// 开启右子树递归 i - left + root + 1 含义为 根节点索引 + 左子树长度 + 1node.right = recur(root + i - left + 1, i + 1, right);// 回溯返回根节点return node;}public class TreeNode {int val;TreeNode left;TreeNode right;TreeNode(int x) {val = x;}}}
二、数值的整数次方

public class Solution {public double myPow(double x, int n) {long b = n;double res = 1.0;if (b < 0) {x = 1 / x;b = -b;}while (b > 0) {if ((b & 1) == 1) {res *= x;}x *= x;b >>= 1;}return res;}
}
三、打印从 1 到最大的 n 位数

public class Solution {public int[] printNumbers(int n) {int[] res = new int[(int) Math.pow(10, n) - 1];for (int i = 0; i < res.length; i++) {res[i] = i + 1;}return res;}
}
四、二叉搜索树的后序遍历序列
public class Solution {public boolean verifyPostorder(int[] postorder) {Stack<Integer> stack = new Stack<>();int root = Integer.MAX_VALUE;for(int i = postorder.length - 1; i >= 0; i--) {if(postorder[i] > root) {return false;}while(!stack.isEmpty() && stack.peek() > postorder[i]) {root = stack.pop();}stack.add(postorder[i]);}return true;}
}
五、数组中的逆序对

public class Solution {int[] nums, tmp;public int reversePairs(int[] nums) {this.nums = nums;tmp = new int[nums.length];return mergeSort(0, nums.length - 1);}private int mergeSort(int l, int r) {// 终止条件if (l >= r) {return 0;}// 递归划分int m = (l + r) / 2;int res = mergeSort(l, m) + mergeSort(m + 1, r);// 合并阶段int i = l, j = m + 1;for (int k = l; k <= r; k++) {tmp[k] = nums[k];}for (int k = l; k <= r; k++) {if (i == m + 1) {nums[k] = tmp[j++];} else if (j == r + 1 || tmp[i] <= tmp[j])nums[k] = tmp[i++];else {nums[k] = tmp[j++];res += m - i + 1; // 统计逆序对}}return res;}
}
相关文章:

【图解算法数据结构】分治算法篇 + Java代码实现
文章目录 一、重建二叉树二、数值的整数次方三、打印从 1 到最大的 n 位数四、二叉搜索树的后序遍历序列五、数组中的逆序对 一、重建二叉树 public class Solution {int[] preorder;HashMap<Integer, Integer> dic new HashMap<>();public TreeNode buildTree(in…...
——Ubuntu开机自动执行命令)
Ubuntu系统环境搭建(八)——Ubuntu开机自动执行命令
ubuntu环境搭建专栏🔗点击跳转 Ubuntu系统环境搭建(八)——Ubuntu开机自动执行命令 修改文件 vim /etc/rc.local以自启动mysql为例,在文件末尾添加 /usr/local/mysql8/bin/mysqld_safe --defaults-file/usr/local/etc/my.cnf …...
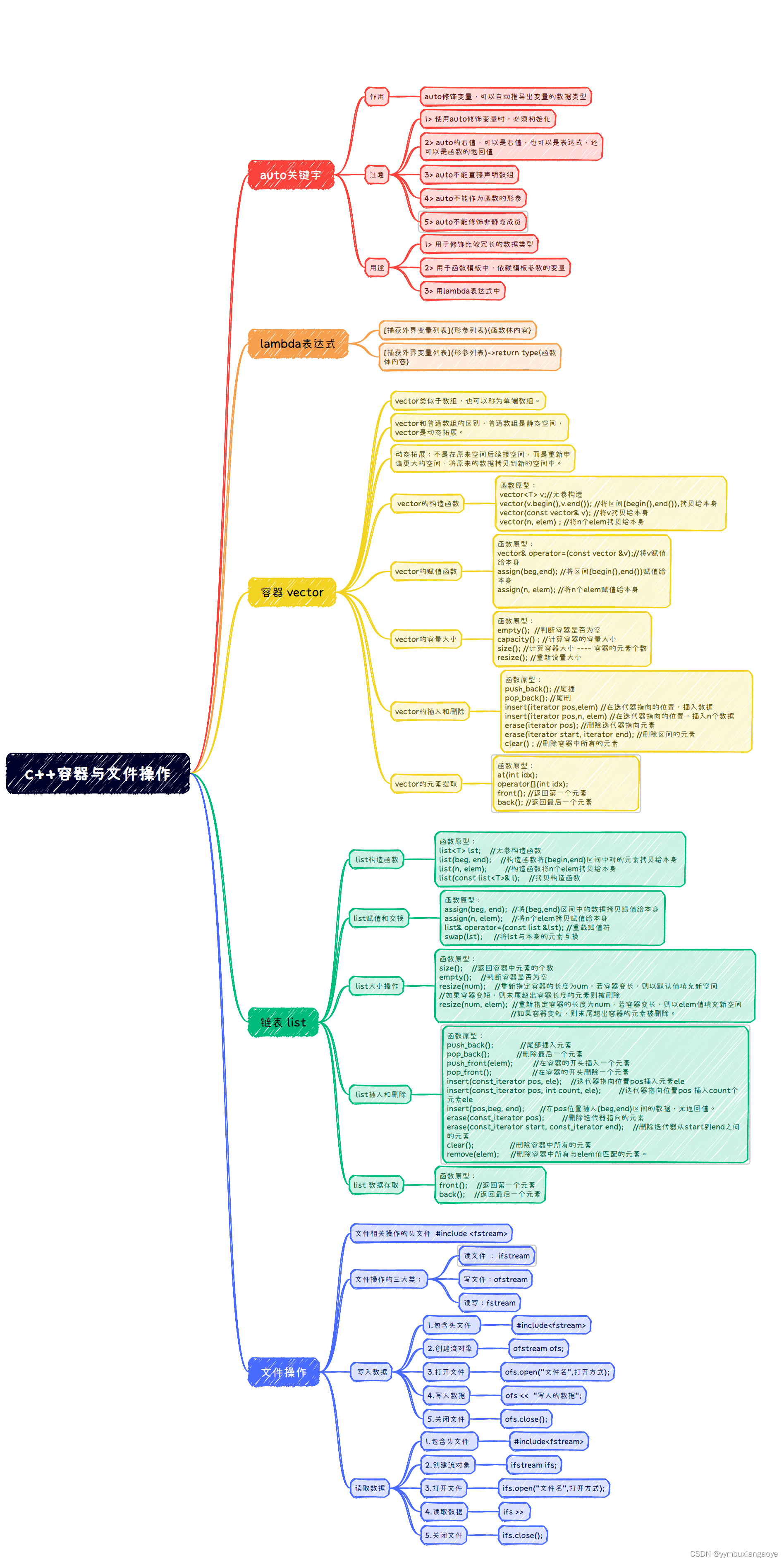
c++(8.29)auto关键字,lambda表达式,数据类型转换,标准模板库,list,文件操作+Xmind
作业: 封装一个学生的类,定义一个学生这样类的vector容器, 里面存放学生对象(至少3个) 再把该容器中的对象,保存到文件中。 再把这些学生从文件中读取出来,放入另一个容器中并且遍历输出该容器里的学生。…...
)
Docker学习笔记(持续更新)
Docker学习目录 1.基础1.1 Docker简介1.1.1 Why Docker?1.1.2 Docker理念1.1.3 容器与虚拟机1.1.4 Docker能做什么? 1.2 Docker的基本组成1.2.1 Docker的三要素1.2.2 Docker平台架构 1.基础 1.1 Docker简介 1.1.1 Why Docker? 在个人笔记本…...

无涯教程-Android - 应用组件
应用程序组件是Android应用程序的基本组成部分,这些组件需要在应用程序清单文件 AndroidManifest.xml 注册,该文件描述了应用程序的每个组件以及它们如何交互。 Android应用程序可以使用以下四个主要组件- Sr.NoComponents & 描述1 Activities 它们…...
树与图c++
1.树 前言 本文主要介绍的数据结构之树型结构的相关知识,树型数据结构是面试官面试的时候非常喜欢考的一种数据结构,树形结构的遍历也是大厂笔试非常喜欢设置的考点,这些内容都会在本篇文章中进行详细的介绍,并且还会介绍一些常…...
中小企业常用的 IT 项目管理软件有哪些?
越热门,越贵的IT项目管理软件越好用吗?对于预算有限的中小型企业来说,如何选择一款适合自己的项目管理工具着实是个头疼的问题。 首先适用于中小型企业使用的 IT 项目管理软件需要具备哪些特点呢? 1、简单易用:中小企…...

汇编原理计算方法:物理地址=段地址*16+偏移地址
文章目录 计算方法计算错误分析 计算方法 根据进制的不同选择不同的计算方法 注意:物理地址、段地址和偏移地址的进制统一,要么都是二进制,要么都是十六进制,一般而言多是十六进制 若是二进制表达,则将段地址左移四…...
jdk-8u371-linux-x64.tar.gz jdk-8u371-windows-x64.exe 【jdk-8u371】 全平台下载
jdk-8u371 全平台下载 jdk-8u371-windows-x64.exejdk-8u371-linux-x64.rpmjdk-8u371-linux-x64.tar.gzjdk-8u371-macosx-x64.dmgjdk-8u371-linux-aarch64.tar.gz 下载地址 迅雷云盘 链接:https://pan.xunlei.com/s/VNdLL3FtCnh45nIBHulh_MDjA1?pwdw4s6 百度…...
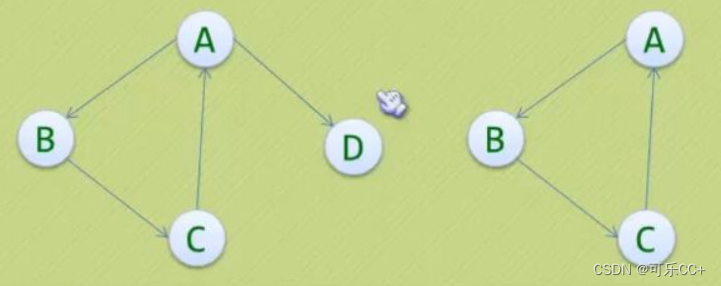
数据结构体--5.0图
目录 一、定义 二、图的顶点与边之间的关系 三、图的顶点与边之间的关系 四、连通图 五、连通图的生成树定义 一、定义 图(Graph)是由顶点的又穷非空集合合顶点之间边的集合组成,通常表示为:G(V,E&…...

深入剖析 Golang 程序启动原理 - 从 ELF 入口点到GMP初始化到执行 main!
大家好,我是飞哥! 在过去的开发工作中,大家都是通过创建进程或者线程来工作的。Linux进程是如何创建出来的? 、聊聊Linux中线程和进程的联系与区别! 和你的新进程是如何被内核调度执行到的? 这几篇文章就是…...
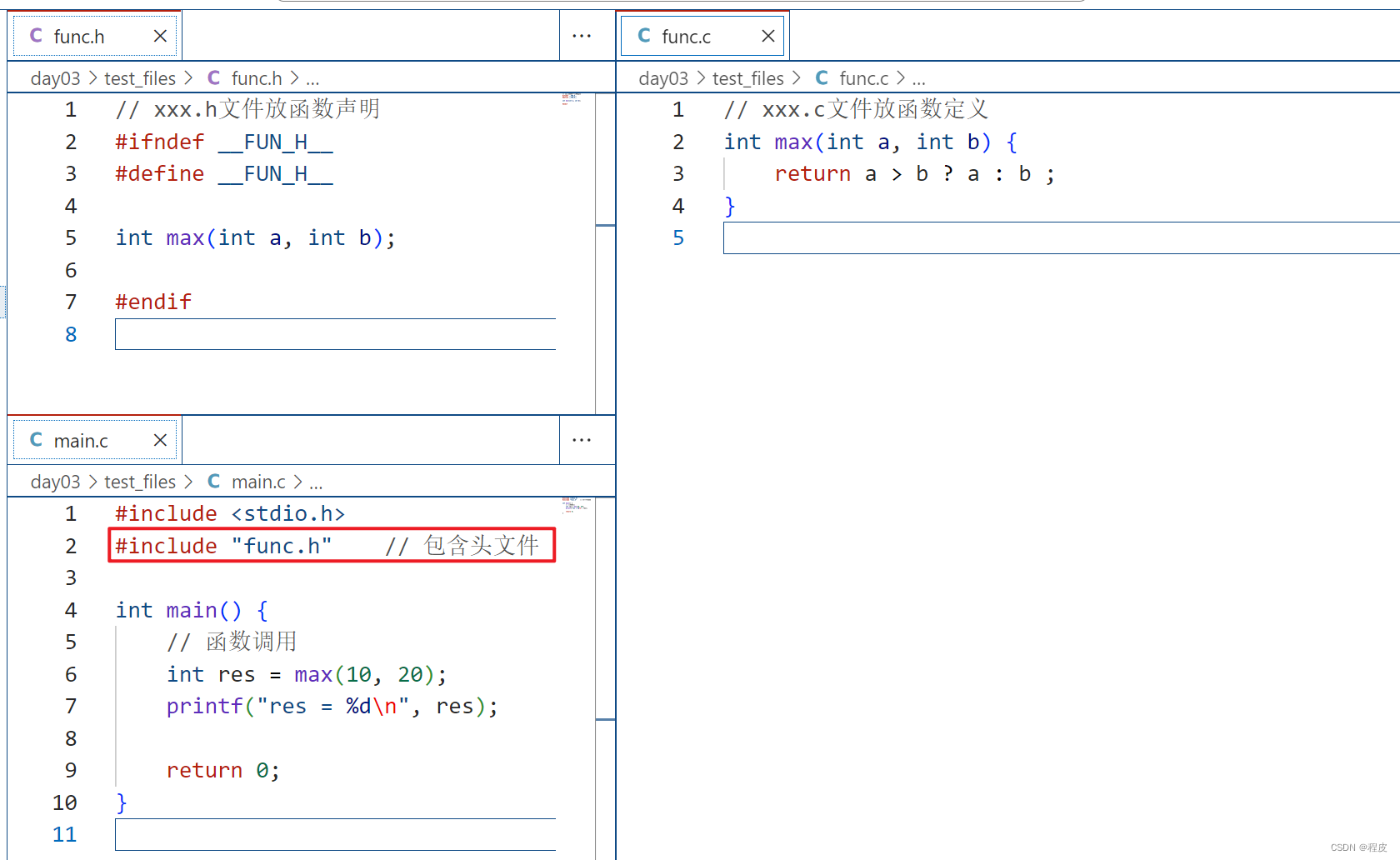
C语言——多文件编程
多文件编程 把函数声明放在头文件xxx.h中,在主函数中包含相应头文件在头文件对应的xxx.c中实现xxx.h声明的函数 防止头文件重复包含 当一个项目比较大时,往往都是分文件,这时候有可能不小心把同一个头文件 include 多次,或者头…...

Git学习part1
02.尚硅谷_Git&GitHub_为什么要使用版本控制_哔哩哔哩_bilibili 1.Git必要性 记录代码开发的历史状态 ,允许很多人同时修改文件(分布式)且不会丢失记录 2.版本控制工具应该具备的功能 1)协同修改 多人并行不悖的修改服务器端…...

2309C++均为某个类型
#include <常用> 构 A{空 f(){打印("啊");} }; 元<类 T>构 是点啊:假型{}; 元<>构 是点啊<A>:真型{}; 元<类 T>概念 是呀是点啊<T>::值;元<是呀...T>空 f(T&...t){(t.f(),...); }//均为元<类...T>要求 均为值&l…...

2023年打脸面试官之TCP--瞬间就懂
1.TCP 三次握手之为什么要三次呢?事不过三? 过程如下图: 先来解释下上述的各个标志的含义 序列号seq:占4个字节,用来标记数据段的顺序,TCP把连接中发送的所有数据字节都编上一个序号,第一个字节…...

设计模式-单例模式Singleton
单例模式 单例模式 (Singleton) (重点)1) 为什么要使用单例2) 如何实现一个单例2.a) 饿汉式2.b) 懒汉式2.c) 双重检查锁2.d) 静态内部类2.e) 枚举类2.f) 反射入侵2.g) 序列化与反序列化安全 3) 单例存在的问题3.a) 无法支持面向对象编程 单例模式 (Singleton) (重点) 一个类只…...

PPPoE连接无法建立的排查和修复
嗨,亲爱的读者朋友们!你是否曾经遇到过PPPoE连接无法建立的问题?今天我将为你详细解析排查和修复这个问题的步骤。 检查物理连接 首先,我们需要确保物理连接没有问题。请按照以下步骤进行检查: - 检查网线是否插好&…...

QT 发布软件基本操作
一、配置环境变量 找到Qt安装时的bin目录的路径:D:\Qt\Qt5.14.2\5.14.2\mingw73_64\bin,将目录拷贝至下述环境变量中。 打开计算机的高级系统设置 选中环境变量-->系统变量-->Path 点击编辑-->新建-->粘贴 二、生成发布软件的可执行程序 …...
CTFhub-SSRF-内网访问
CTFHub 环境实例 | 提示信息 http://challenge-8bf41c5c86a8c5f4.sandbox.ctfhub.com:10800/?url_ 根据提示,在url 后门添加 127.0.0.1/flag.php http://challenge-8bf41c5c86a8c5f4.sandbox.ctfhub.com:10800/?url127.0.0.1/flag.php ctfhub{a6bb51530c8f6be0…...

Cenos7安装小火车程序动画
运维Shell脚本小试牛刀(一) 运维Shell脚本小试牛刀(二) 运维Shell脚本小试牛刀(三)::$(cd $(dirname $0); pwd)命令详解 运维Shell脚本小试牛刀(四): 多层嵌套if...elif...elif....else fi_蜗牛杨哥的博客-CSDN博客 Cenos7安装小火车程序动画 一:替换…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...
