【分类】分类性能评价
评价指标
1、准确率、召回率、精确率、F-度量、ROC
属于各类的样本的并不是均一分布,甚至其出现概率相差很多个数量级,这种分类问题称为不平衡类问题。在不平衡类问题中,准确率并没有多大意义,我们需要一些别的指标。
通常在不平衡类问题中,我们使用F-度量来作为评价模型的指标。以二元不平衡分类问题为例,预测只可能出现4种状况:
a) 将正类样本预测为正类(True Positive, TP) b) 将负类样本预测为正类(False Positive, FP)
c) 将正类样本预测为负类(False Negative, FN) d) 将负类样本预测为负类(True Negative, TN)

- 对于测试集中 N N N个样本,有 M M M个被正确分类,则准确率(正确率)为:
准确率 ( A c c u r a c y ) = M N 准确率(Accuracy) =\frac{M}{N} 准确率(Accuracy)=NM
- 定义召回率(recall):不能接受漏报,预测到所有想被预测到的样本
召回率 ( r e c a l l ) = 被预测为正类的 原本的正类 = ∣ T P ∣ ∣ T P ∣ + ∣ F N ∣ 召回率(recall)=\frac{被预测为正类的}{原本的正类}=\frac{|TP|}{|TP|+|FN|} 召回率(recall)=原本的正类被预测为正类的=∣TP∣+∣FN∣∣TP∣
-
定义精确率(precision):不能接受误检,预测结果尽可能不出错
精确率 ( p r e c i s i o n ) = 被预测为正类的 预测的正类 = ∣ T P ∣ ∣ T P ∣ + ∣ F P ∣ 精确率(precision)=\frac{被预测为正类的}{预测的正类}=\frac{|TP|}{|TP|+|FP|} 精确率(precision)=预测的正类被预测为正类的=∣TP∣+∣FP∣∣TP∣ -
F F F-度量则是在召回率与精确率之间去调和平均数;
F α = ( 1 + α 2 ) R P R + α P F 1 = 2 R P R + P F_{ \alpha}=\frac{(1+\alpha ^2)RP}{R+\alpha P}\\ F_{1}=\frac{2RP}{R+P} Fα=R+αP(1+α2)RPF1=R+P2RP
精确率:分母是预测到的正类,精确率的提出是让模型的现有预测结果尽可能不出错(宁愿漏检,也不能让现有的预测有错)
以地震模型为例说就是宁愿地震了没报,也不能误报地震,比如说为了不错报,只预测了第50天可能发生地震,此时的
1.精确率:1/1=100%
2.召回率:1/2=50%
虽然有一次地震没预测到,但是我们做出的预测都是对的。
召回率:分母是原本的正类,召回率的提出是让模型预测到所有想被预测到的样本(就算多预测一些错的,也能接受)
以地震模型为例说这100次地震,比如说为了不漏报,预测了第30天、50天、51天、70天、85天地震,此时的
1.精确率:2/5=40%
2.召回率:2/2=100%
虽然预测错了3次,但是我们把会造成灾难的2次地震全预测到了。
精确率和召回率有什么用?为什么需要它?通俗讲解(人话)
上面我们已经讲的很清楚了,这里以两种需求为例
- 预测地震 - 不能接受漏报
- 人脸识别支付(银行人脸支付) - 不能接受误检
人脸识别支付:主要提升精确率,更倾向于不能出现错误的预测。
应用场景:你刷脸支付时就算几次没检测到你的脸,最多会让你愤怒,对银行损失不大,但是如果把你的脸检测成别人的脸,就会出现金融风险,让别人替你买单,对银行损失很大。所以宁愿让你付不了钱,也不会让别人帮你付钱。
预测地震:主要提升召回率,更倾向于宁愿多预测一些错的也不能漏检。
应用场景:地震预测时宁愿多预测一些错的,也不想漏掉一次地震,预测错误最多会让大家多跑几趟,造成少量损失。只要预测对一次,就会挽回百亿级别的损失,之前所有的损失都值了。
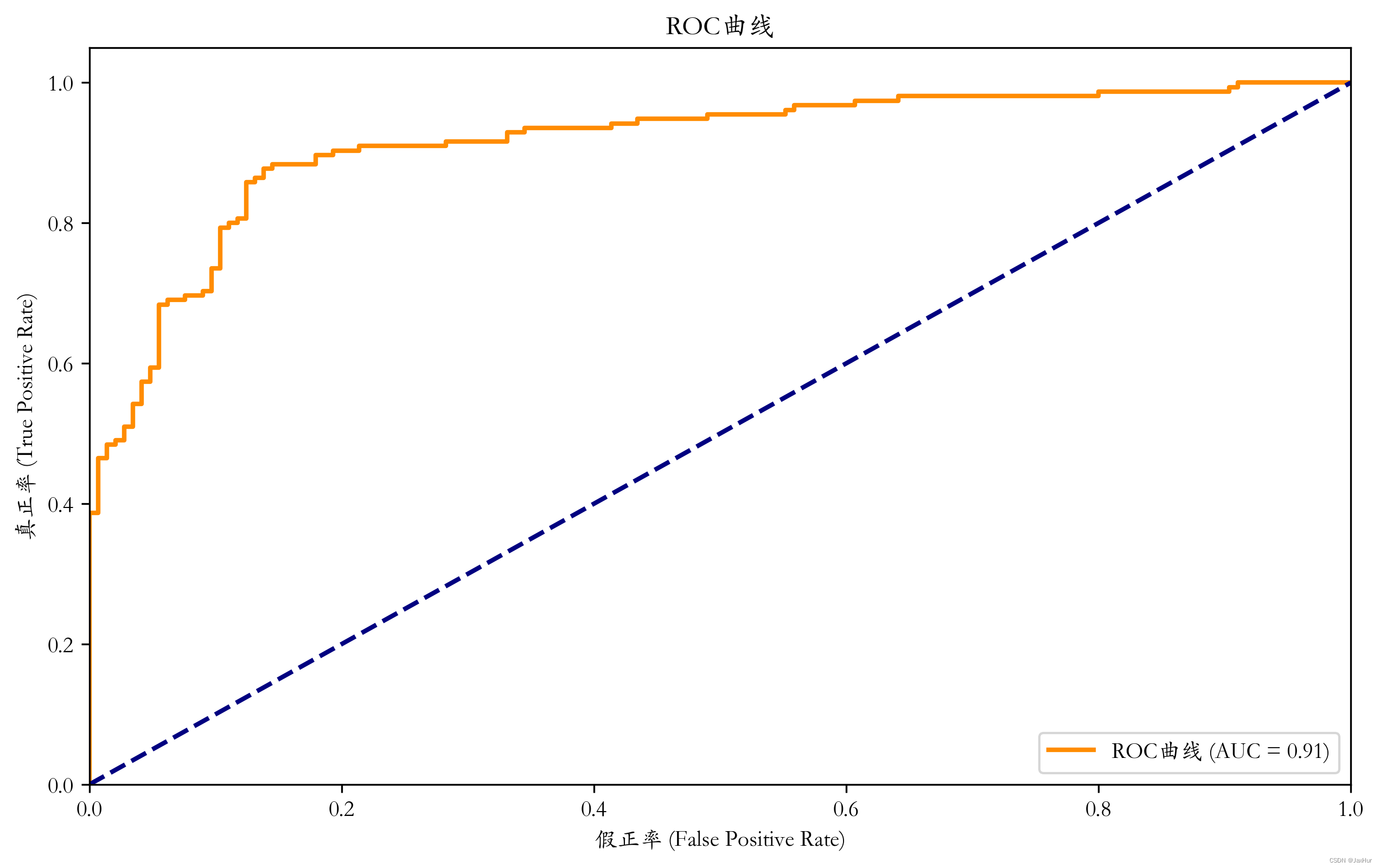
ROC曲线(Receiver Operating Characteristic,受试者操作特征)
通常情况下,我们希望ROC曲线越靠近左上角,这表示模型在各种阈值下都表现良好,同时具有高的真正率和低的假正率,而AUC值(曲线下面积)也可以用来衡量模型的整体性能,越接近1表示模型性能越好。
画ROC曲线步骤:
- 根据分类模型得出每个样本属于正类的概率,根据概率将样本由高到低排列
- 将样本为正类的概率由高到低,依次作为阈值 t t t,大于等于 t t t则为正类,小于t视为反类
- 使用真正率 T P R = T P T P + F N TPR=\frac{TP}{TP+FN} TPR=TP+FNTP作为竖轴,假正率 F P R = F P F P + T N FPR=\frac{FP}{FP+TN} FPR=FP+TNFP作为横轴,对于每个选定的阈值均能产生一个对应的点。
例子:
| 样本编号 | 分类 | 预测为正类的概率 | TPR | FPR |
|---|---|---|---|---|
| 1 | 正类 | 0.98 | 1 1 + 14 = 1 15 \frac{1}{1+14}=\frac{1}{15} 1+141=151 | 0 0 + 5 = 0 5 \frac{0}{0+5}=\frac{0}{5} 0+50=50 |
| 2 | 正类 | 0.96 | 2 2 + 13 = 2 15 \frac{2}{2+13}=\frac{2}{15} 2+132=152 | 0 0 + 5 = 0 5 \frac{0}{0+5}=\frac{0}{5} 0+50=50 |
| 3 | 正类 | 0.92 | 3 3 + 12 = 3 15 \frac{3}{3+12}=\frac{3}{15} 3+123=153 | 0 0 + 5 = 0 5 \frac{0}{0+5}=\frac{0}{5} 0+50=50 |
| 4 | 正类 | 0.88 | 4 4 + 11 = 4 15 \frac{4}{4+11}=\frac{4}{15} 4+114=154 | 0 0 + 5 = 0 5 \frac{0}{0+5}=\frac{0}{5} 0+50=50 |
| 5 | 正类 | 0.85 | 5 5 + 10 = 5 15 \frac{5}{5+10}=\frac{5}{15} 5+105=155 | 0 0 + 5 = 0 5 \frac{0}{0+5}=\frac{0}{5} 0+50=50 |
| 6 | 正类 | 0.83 | 6 6 + 9 = 6 15 \frac{6}{6+9}=\frac{6}{15} 6+96=156 | 0 0 + 5 = 0 5 \frac{0}{0+5}=\frac{0}{5} 0+50=50 |
| 7 | 反类 | 0.82 | 6 6 + 9 = 6 15 \frac{6}{6+9}=\frac{6}{15} 6+96=156 | 1 1 + 4 = 1 5 \frac{1}{1+4}=\frac{1}{5} 1+41=51 |
| 8 | 正类 | 0.8 | 7 7 + 8 = 7 15 \frac{7}{7+8}=\frac{7}{15} 7+87=157 | 1 1 + 4 = 1 5 \frac{1}{1+4}=\frac{1}{5} 1+41=51 |
| 9 | 正类 | 0.78 | 8 8 + 7 = 8 15 \frac{8}{8+7}=\frac{8}{15} 8+78=158 | 1 1 + 4 = 1 5 \frac{1}{1+4}=\frac{1}{5} 1+41=51 |
| 10 | 反类 | 0.71 | 8 8 + 7 = 8 15 \frac{8}{8+7}=\frac{8}{15} 8+78=158 | 2 2 + 3 = 2 5 \frac{2}{2+3}=\frac{2}{5} 2+32=52 |
| 11 | 正类 | 0.68 | 9 9 + 6 = 9 15 \frac{9}{9+6}=\frac{9}{15} 9+69=159 | 2 2 + 3 = 2 5 \frac{2}{2+3}=\frac{2}{5} 2+32=52 |
| 12 | 正类 | 0.64 | 10 10 + 5 = 10 15 \frac{10}{10+5}=\frac{10}{15} 10+510=1510 | 2 2 + 3 = 2 5 \frac{2}{2+3}=\frac{2}{5} 2+32=52 |
| 13 | 正类 | 0.59 | 11 11 + 4 = 11 15 \frac{11}{11+4}=\frac{11}{15} 11+411=1511 | 2 2 + 3 = 2 5 \frac{2}{2+3}=\frac{2}{5} 2+32=52 |
| 14 | 正类 | 0.55 | 12 12 + 3 = 12 15 \frac{12}{12+3}=\frac{12}{15} 12+312=1512 | 2 2 + 3 = 2 5 \frac{2}{2+3}=\frac{2}{5} 2+32=52 |
| 15 | 反类 | 0.52 | 12 12 + 3 = 12 15 \frac{12}{12+3}=\frac{12}{15} 12+312=1512 | 3 3 + 2 = 3 5 \frac{3}{3+2}=\frac{3}{5} 3+23=53 |
| 16 | 正类 | 0.51 | 13 13 + 2 = 13 15 \frac{13}{13+2}=\frac{13}{15} 13+213=1513 | 3 3 + 2 = 3 5 \frac{3}{3+2}=\frac{3}{5} 3+23=53 |
| 17 | 正类 | 0.5 | 14 14 + 1 = 14 15 \frac{14}{14+1}=\frac{14}{15} 14+114=1514 | 3 3 + 2 = 3 5 \frac{3}{3+2}=\frac{3}{5} 3+23=53 |
| 18 | 反类 | 0.48 | 14 14 + 1 = 14 15 \frac{14}{14+1}=\frac{14}{15} 14+114=1514 | 4 4 + 1 = 4 5 \frac{4}{4+1}=\frac{4}{5} 4+14=54 |
| 19 | 正类 | 0.42 | 15 15 + 0 = 15 15 \frac{15}{15+0}=\frac{15}{15} 15+015=1515 | 4 4 + 1 = 4 5 \frac{4}{4+1}=\frac{4}{5} 4+14=54 |
| 20 | 反类 | 0.2 | 15 15 + 0 = 15 15 \frac{15}{15+0}=\frac{15}{15} 15+015=1515 | 1 |

ROC曲线下方面积为 A U C AUC AUC, A U C AUC AUC值越大,表示分类模型的预测准确性越高, R O C ROC ROC曲线越光滑,一般表示过拟合现象较轻(为什么??
2.各项指标的python实现,以logistic回归为例
import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics import accuracy_score, precision_score, recall_score, roc_curve, auc
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression
plt.rcParams['font.sans-serif']=['STKaiTi'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
# 创建一个示例分类数据集
X, y = make_classification(n_samples=1000, n_features=20, random_state=42)# 将数据集分成训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)# 训练一个分类模型,例如Logistic回归
model = LogisticRegression(random_state=42)
model.fit(X_train, y_train)# 在测试集上进行预测
y_pred = model.predict(X_test)# 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print(f'准确率 (Accuracy): {accuracy:.2f}')# 计算召回率
recall = recall_score(y_test, y_pred)
print(f'召回率 (Recall): {recall:.2f}')# 计算精确率
precision = precision_score(y_test, y_pred)
print(f'精确率 (Precision): {precision:.2f}')# 计算F1指标
F1 = 2*recall*precision/(recall+ precision)
print(f'F1={F1}')#ROC曲线和AUC值
fpr, tpr, thresholds = roc_curve(y_test, model.predict_proba(X_test)[:, 1])
roc_auc = auc(fpr, tpr)# 可视化ROC曲线
plt.figure(figsize=(10, 6),dpi = 300)
plt.plot(fpr, tpr, color='darkorange', lw=2, label=f'ROC曲线 (AUC = {roc_auc:.2f})')
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('假正率 (False Positive Rate)')
plt.ylabel('真正率 (True Positive Rate)')
plt.title('ROC曲线')
plt.legend(loc='lower right')
plt.show()结果:
准确率 (Accuracy): 0.85
召回率 (Recall): 0.83
精确率 (Precision): 0.88
F1=0.8504983388704319
评价方法
- 保留法:划分训练集于测试集,比例不清楚,没有k-折交叉验证好
- k-折交叉验证:将样本随机划分为k个大小相等的子集,在每一轮交叉验证种,选择一个子集作为测试集,重复k轮,保证每个子集都作为测试集出现,对k轮检验结果取平均值作为评价表中
- 蒙特卡洛交叉验证:多次保留法,某些样本可能只出现在测试集中
相关文章:

【分类】分类性能评价
评价指标 1、准确率、召回率、精确率、F-度量、ROC 属于各类的样本的并不是均一分布,甚至其出现概率相差很多个数量级,这种分类问题称为不平衡类问题。在不平衡类问题中,准确率并没有多大意义,我们需要一些别的指标。 通…...

M1 Pro 新芯片安装python2 方案汇总
前言:磨刀不误砍柴工,环境装好,才能打工。M1 Pro 新芯片安装python2 文章目录 方案一 docker 容器构造环境(如果涉及本地两个仓库需要关联则不适用)方案二 使用 pyenv 🚀 作者简介:作为某云服务…...

无涯教程-Android - Broadcast Receivers
Broadcast Receivers 仅响应来自其他应用程序或系统本身的广播消息,这些消息有时称为events或intents。例如,应用程序还可以启动广播,以使其他应用程序知道某些数据已下载到设备并可供他们使用,因此广播接收器将拦截此通信并启动适…...

【Pytorch】Tutorials个人翻译集合
本文记录Pytorch Tutorials文档的翻译文章集合. 由于本人英语能力有限(only-CET4),欢迎指正翻译中的错误。 Introduction to PyTorch 【Pytorch】Pytorch文档学习1:Tensors 【Pytorch】Pytorch文档学习2:DATASETS &a…...

WordPress(6)网站侧边栏倒计时进度小工具
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 效果图在这里插入图片描述一、添加位置二、主题style.css文件中添加美化1.引入库2.添加自定义的HTML模块效果图 提示:以下是本篇文章正文内容,下面案例可供参考 一、添加位置 在主题中 child.js…...
uniapp小程序单页面改变手机电量,头部通知的颜色效果demo(整理)
onShow(){ // 改变电池的颜色 wx.setNavigationBarColor({ frontColor: ‘#ffffff’, //只支持两种颜色 backgroundColor: ‘#ffffff’, animation: { duration: 1 } }) }...
数据挖掘导论学习笔记1(第1 、2章)
参考:https://blog.csdn.net/u013232035/article/details/48281659?spm1001.2014.3001.5506 和《数据挖掘导论》学习笔记(第1-2章)_时机性样本_schdut的博客-CSDN博客 第1章 绪论 数据挖掘是一种技术,它将传统的数据分析方法…...

从零开始,探索C语言中的字符串
字符串 1. 前言2. 预备知识2.1 字符2.2 字符数组 3. 什么是字符串4. \04.1 \0是什么4.2 \0的作用4.2.1 打印字符串4.2.2 求字符串长度 1. 前言 大家好,我是努力学习游泳的鱼。你已经学会了如何使用变量和常量,也知道了字符的概念。但是你可能还不了解由…...

Ubuntu学习---跟着绍发学linux课程记录(第二部分)
文章目录 7 文件权限7.1 文件的权限7.2 修改文件权限7.3 修改文件的属主 8、可执行脚本8.2Shell脚本8.3python脚本的创建 9Shell9.1Shell中的变量9.2 环境变量9.3用户环境变量 学习链接: Ubuntu 21.04乌班图 Linux使用教程_60集Linux课程 所有资料在 http://afanihao.cn/java …...

React18 新特性
React18 新特性 自动批量更新State 定义 import { useState } from reactconst [x, setX] useState(0)渲染赋值 setX(5)并发CM模式 同步不可中断更新机制 -> 异步可中断并行 状态更新 机制 React18 默认开启并发模式 详见代码 ReactDOM 的引入 import ReactDOM fr…...
HarmonyOS Codelab 优秀样例——购物应用,体验一次开发多端部署魅力
一. 样例介绍 本篇Codelab基于自适应布局和响应式布局,实现购物应用在手机、折叠屏、平板不同屏幕尺寸设备上按不同设计显示。通过三层工程结构组织代码,实现一次开发,多端部署 。 手机运行效果如图所示: 折叠屏运行效果图&#x…...
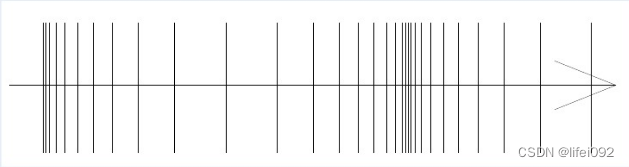
音频基本知识
声音传播方式: 1)声音的传播需要介质,在真空中不能传播; 2)声波属于纵波,即如下图传播方向与振动方向一致; 声音速度: 1)常温常压下,一般空气速度为340m/s; 2)温度越高,声速越大; 3)液体、固体的传播速度比空气快; 人耳可接收到的频域范围: 1)通常范围…...
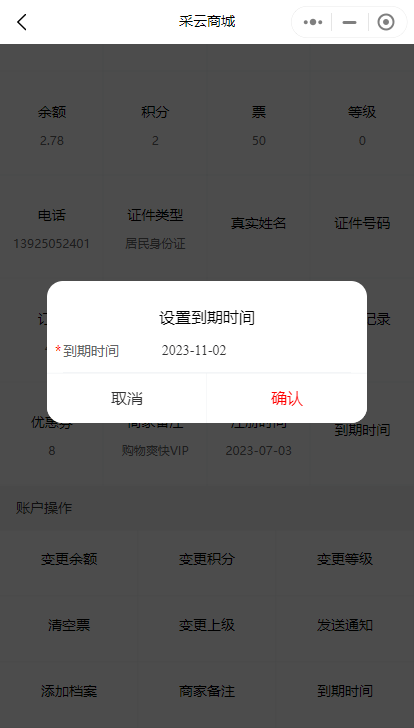
小程序中如何给会员卡设置到期时间
通过设置会员卡到期时间,可以有效地管理会员卡的使用周期,提供更好的会员服务体验。下面将介绍一种常见的给会员卡设置到期时间的方法。 1. 找到指定的会员卡。在管理员后台->会员管理处,找到需要设置到期时间的会员卡。也支持对会员卡按…...

Cookie与Session的区别及如何选择
目录 Cookie Session 如何选择 在网站开发中,Cookie与Session是两种常见的数据管理方式,它们在不同情况下有各自的优势和劣势。在这篇文章中,我们将深入了解Cookie与Session之间的区别,并提供了一些建议,帮助您在实…...

【快手小玩法-弹幕游戏】开发者功能测试报告提交模板
背景 快手有明确的要求,准入和准出更加严格,要求有明确的测试报告。格式如下: *本文参考字节wiki:CP侧测试报告模板(复制填写轻雀文档) 其他文章推荐:【抖音小玩法-弹幕游戏】开发者功能测试报告提交模板 一、前言…...

微信小程序在线阅读系统微信小程序设计与实现
摘 要:信息技术永远是改变生活的第一种创新方式,各种行业的发展更是脱离不了科技化的支持。原本传统的行业正在被科技行业的切入悄悄的发生变化。就拿我们生活当中常见的事情举例而言,在外卖行业还没有发展的快速的时候,方便面等速…...
【OpenCV入门】第七部分——图像的几何变换
文章结构 缩放dsize参数实现缩放fx参数和fy参数实现缩放 翻转仿射变换平移旋转倾斜 透视cmath模块 缩放 通过resize()方法可以随意更改图像的大小比例: dst cv2.resize(src, dsize, fx, fy, interpolation)src: 原始图像dsize: 输出图像的…...
)
淘宝app商品详情原数据接口API(支持高并发请求/免费测试)
item_get_app-获得淘宝app商品详情原数据 一、引言 随着移动互联网的迅速发展,移动电商应用的需求也在不断增长。淘宝作为中国最大的电商平台之一,每天需要处理大量的商品数据和用户访问请求。为了提供更加优质的用户体验,淘宝开放了商品详…...
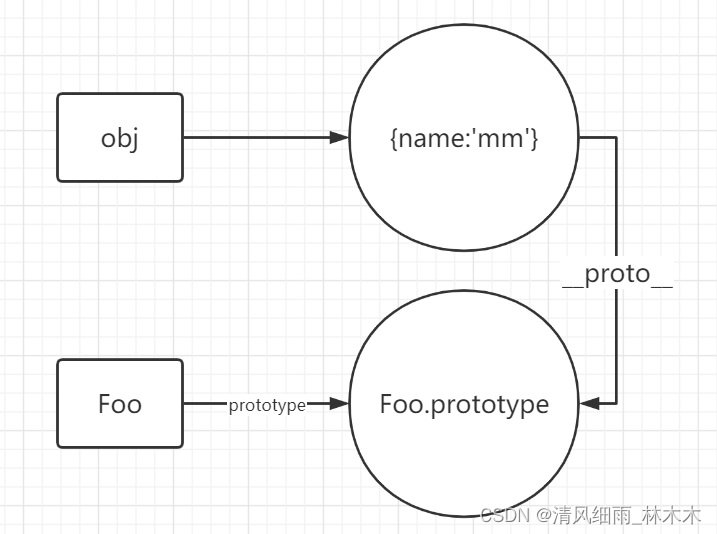
JS中的new操作符
文章目录 JS中的new操作符一、什么是new?二、new经历了什么过程?三、new的过程分析四、总结 JS中的new操作符 参考:https://www.cnblogs.com/buildnewhomeland/p/12797537.html 一、什么是new? 在JS中,new的作用是通过…...

文件编辑器、用户管理,嘎嘎学
打开文件 vim # 首先你先得下载这个插件 yum install -y vim vim 文件名 进入编辑模式 i #在光标所在处进入编辑模式 a #在当前光标后面进入编辑模式 o #在光标的下一行进入编辑模式 I #在光标所在处行首进入编辑模式 A #在光标所在处行尾进入编辑模式 O #在光标的上一…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...
