当前位置： 首页 > news >正文

Acwing 897. 最长公共子序列 (每日一题）

news 2026/2/11 0:56:58

最长公共子序列

题目描述

给定两个长度分别为 N 和 M 的字符串 A 和 B，求既是 A 的子序列又是 B 的子序列的字符串长度最长是多少。
输入格式

第一行包含两个整数 N和 M。

第二行包含一个长度为 N 的字符串，表示字符串 A。

第三行包含一个长度为 M 的字符串，表示字符串 B。

字符串均由小写字母构成。
输出格式

输出一个整数，表示最大长度。
数据范围

1≤N,M≤1000

输入样例：

4 5
acbd
abedc

输出样例：

3

状态表示：

集合：所有从A[1,i] B[1,j]的公共子序列的集合

属性：max

像最长上升子序列，状态的划分依据是找不同的点。最长上升子序列确定以a[i]为结尾的子序列，共同点便是以a[i]作为结尾。划分依据：a[1,i-1]中的每个数作为最后一个不同点进行划分**
有没有发现：

DP基操：

1.找不同和相同之处/不同和固定之处
2.结合定义出发！
最长公共子序列的不同点在于i,j在不在序列中，可以将集合划分为4类。
实际上只有3类，且往下看。
(1)i、j 均不在

i、j均不包含其中，那只能从a[i-1]、b[j-1]中去选
得到如下状态转移方程:
f [ i ] [ j ] = f [ i − 1 ] [ j − 1 ] f[i][j]=f[i-1][j-1] f[i][j]=f[i−1][j−1]
(2)i不在，j在

i不在序列中，只能从前i-1中选，j可在可不在。

刚好i不在，j在，包含在这种情况中，且最大值/最小值是可以允许重复的。
得到如下状态转移方程:
f [ i ] [ j ] = f [ i − 1 ] [ j ] f[i][j]=f[i-1][j] f[i][j]=f[i−1][j]
(3)i在，j不在

j不在序列中，那j只能从j-1中选择。i可在可不在。

刚好**i在，j**不在，包含在这种情况中，且最大值/最小值是可以允许重复的。
得到如下状态转移方程:
f [ i ] [ j ] = f [ i ] [ j − 1 ] f[i][j]=f[i][j-1] f[i][j]=f[i][j−1]

(4)i、j均在

只有满足**a[i]==b[j]这一条件才存在。

确定了**a[i]、b[j]之后，剩下的从i-1、j-1中选出最长公共子序列，从定义出发，恰好就是f[i-1][j-1]中选。最后再加上固定好的a[i]、b[j]这一对即可。
得到如下状态转移方程:
f [ i ] [ j ] = f [ i − 1 ] [ j − 1 ] + 1 f[i][j]=f[i-1][j-1]+1 f[i][j]=f[i−1][j−1]+1
最后，(1)是既可以包含在(2)也可以包含在(3)中的，允许最值重复。重复没关系，求出的必定是最值且包含在整个集合中，是合法的。最后，总共只有3种情况。

求和/求值则不允许重复！！！

Accode

import java.util.*;
public class Main{static int N=1010;static int f[][]=new int[N][N];public static void main(String []args){Scanner sc=new Scanner(System.in);int n=sc.nextInt();int m=sc.nextInt();char a[]=(" "+sc.next()).toCharArray();char b[]=(" "+sc.next()).toCharArray();for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){//情况1包含在情况2、3中//情况2、3取一个maxf[i][j]=Math.max(f[i-1][j],f[i][j-1]);//满足a[i]==b[j]这一条件//再与情况4取一个maxif(a[i]==b[j])f[i][j]=Math.max(f[i][j],f[i-1][j-1]+1);}}//输出集合定义System.out.println(f[n][m]);    }
}

往期回顾

不清楚蓝桥杯考什么的点点下方👇

考点秘籍

想背纯享模版的伙伴们点点下方👇

蓝桥杯省一你一定不能错过的模板大全(第一期)

蓝桥杯省一你一定不能错过的模板大全（第二期）

蓝桥杯省一你一定不能错过的模板大全（第三期）

蓝桥杯省一你一定不能错过的模板大全（第四期）！！！

想背注释模版的伙伴们点点下方👇

蓝桥杯必背第一期

蓝桥杯必背第二期

往期精彩回顾

蓝桥杯上岸每日N题 第一期(一)！！！

蓝桥杯上岸每日N题第一期(二)！！！

蓝桥杯上岸每日N题第一期(三)！！！

蓝桥杯上岸每日N题第二期(一)！！！

蓝桥杯上岸每日N题第三期(一)！！！

蓝桥杯上岸每日N题 第四期(最少刷题数)！！！

蓝桥杯上岸每日N题 第五期(山)！！！

蓝桥杯上岸每日N题 第六期(求阶乘)！！！

蓝桥杯上岸每日N题 第七期(小猫爬山)！！！

蓝桥杯上岸每日N题 第八期 (全球变暖)！！！

蓝桥杯每日N题 (消灭老鼠)

蓝桥杯每日N题（杨辉三角形）

蓝桥杯每日N题 (砝码称重)

蓝桥杯上岸每日N题(鸡尾酒)

操作系统期末题库 第九期(完结)

LeetCode Hot100 刷题(第三期)

idea创建SpringBoot项目报错解决方案

数据库SQL语句（期末冲刺）

想看JavaB组填空题的伙伴们点点下方 👇

填空题

竞赛干货

算法竞赛字符串常用操作大全

蓝桥杯上岸必刷！！！(模拟/枚举专题)

蓝桥杯上岸必背！！！ (第三期 DP)

蓝桥杯上岸必背！！！(第四期DFS)

蓝桥杯上岸必背！！！(第五期BFS)

蓝桥杯上岸必背！！！(第六期树与图的遍历)

蓝桥杯上岸必背！！！(第七期 最短路算法)

蓝桥杯上岸必背！！！(第八期 简单数论)

蓝桥杯上岸必刷！！！(进制、数位专题)

蓝桥杯上岸考点清单 (冲刺版）！！！

蓝桥杯上岸必背模板 (纯享版）

相关文章：

Acwing 897. 最长公共子序列 (每日一题）

最长公共子序列 题目描述 给定两个长度分别为 N 和 M 的字符串 A 和 B&#xff0c;求既是 A 的子序列又是 B 的子序列的字符串长度最长是多少。 输入格式 第一行包含两个整数 N和 M。 第二行包含一个长度为 N 的字符串&#xff0c;表示字符串 A。 第三行包含一个长度为 M …...

编程日记 2023/9/3 6:06:10

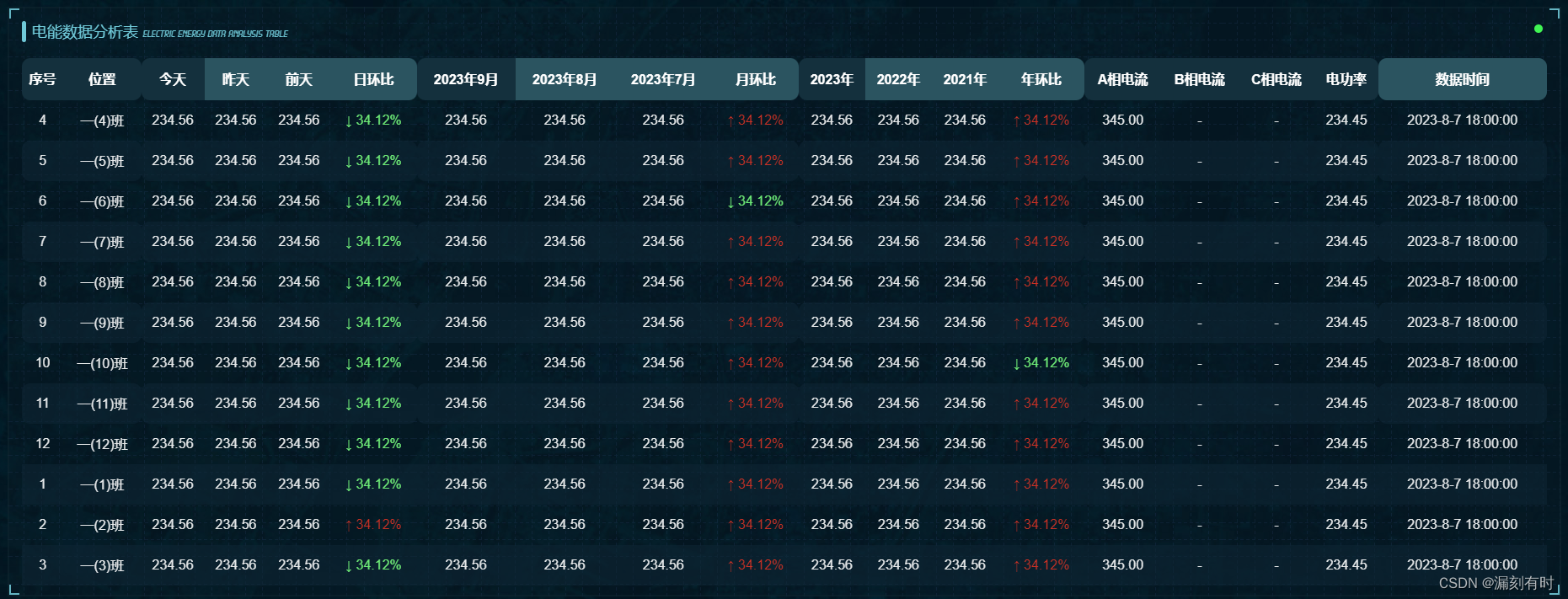
CSS中border-radius的来美化table的实战方案

border-radius是一种CSS属性&#xff0c;用于设置元素的边框的圆角程度。其具体的用法如下&#xff1a; 设置一个值&#xff1a;可以为元素设置一个单一的圆角半径&#xff0c;这个半径将应用于元素的四个角。例如&#xff1a; div {border-radius: 10px; }设置四个值&#x…...

编程日记 2023/9/3 6:05:09

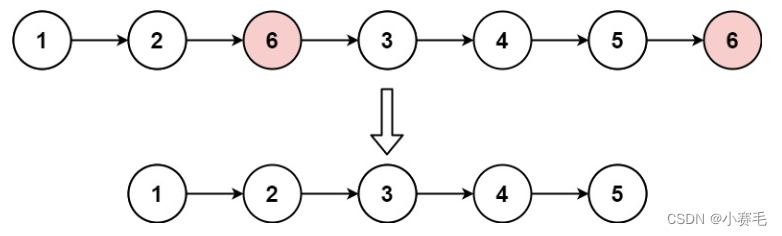
移除链表元素_每日一题

“路虽远&#xff0c;行则将至” ❤️主页&#xff1a;小赛毛 ☕今日份刷题&#xff1a;移除链表元素 题目描述&#xff1a; 给你一个链表的头节点 head 和一个整数 val &#xff0c;请你删除链表中所有满足 Node.val val 的节点&#xff0c;并返回 新的头节点 。 示例1&…...

编程日记 2023/9/3 6:04:08

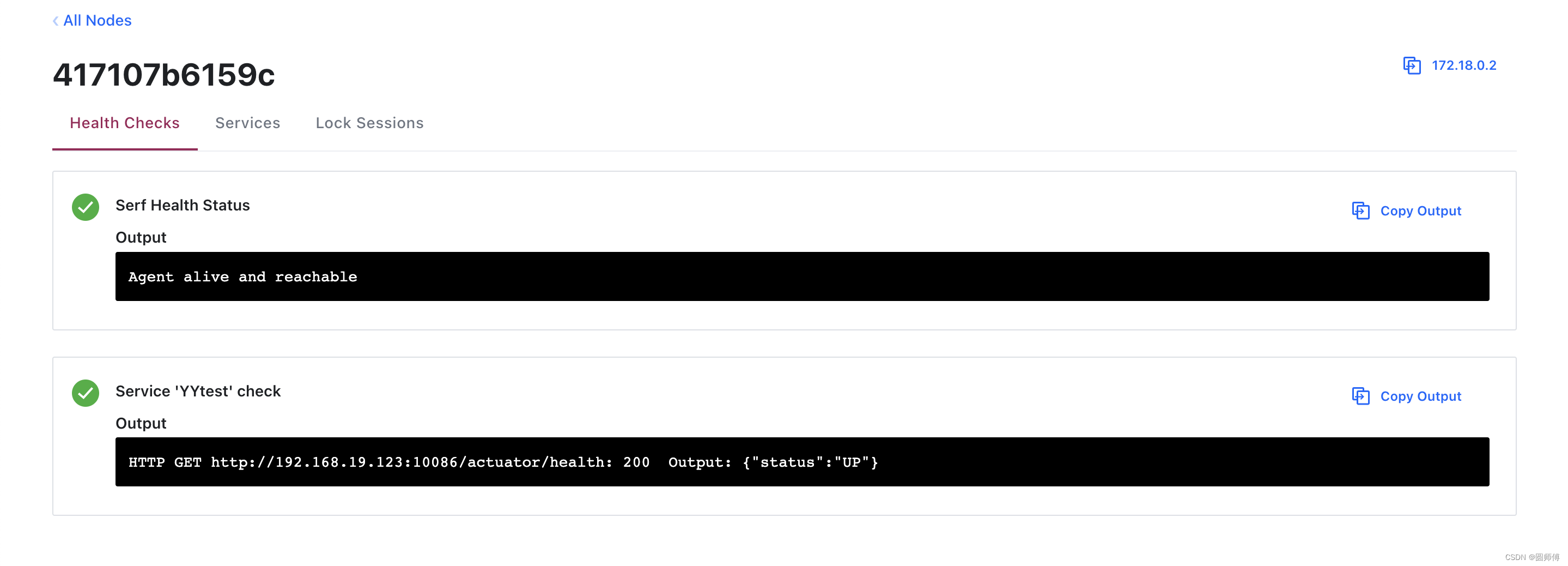
spring boot + Consul 示例 (Kotlin版)

文章目录 1.docker 安装consul2.创建基于springboot的client2.1 依赖版本2.2 pom.xml2.3 启动类2.4 application.properties 3 搭建完成4. 总结 1.docker 安装consul docker-compose.yaml version: "3"services:consul:image: consul:1.4.4container_name: consule…...

编程日记 2023/9/3 6:03:07

Git企业开发控制理论和实操-从入门到深入（四）｜Git的远程操作｜Gitee

前言 那么这里博主先安利一些干货满满的专栏了&#xff01; 首先是博主的高质量博客的汇总&#xff0c;这个专栏里面的博客&#xff0c;都是博主最最用心写的一部分&#xff0c;干货满满&#xff0c;希望对大家有帮助。 高质量博客汇总 然后就是博主最近最花时间的一个专栏…...

编程日记 2023/9/3 6:02:06

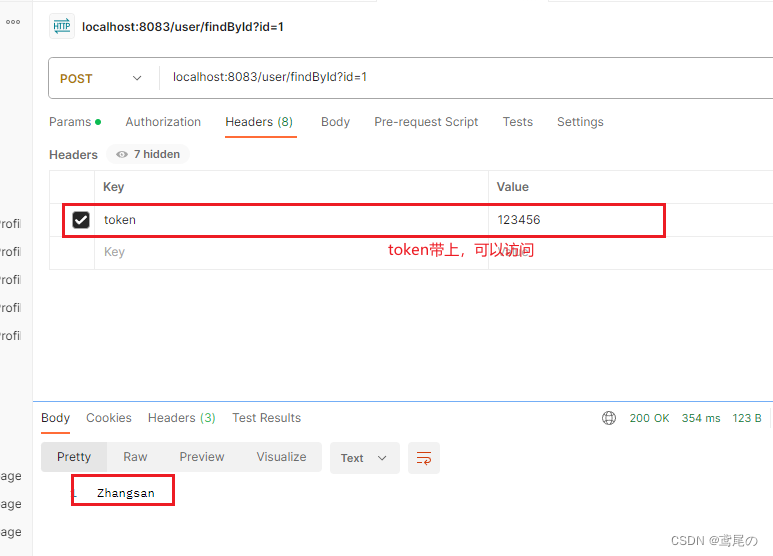
SpringCloudAlibaba Gateway(二)详解-内置Predicate、Filter及自定义Predicate、Filter

Predicate(断言) ​ Predicate(断言)&#xff0c;用于进行判断&#xff0c;如果返回为真&#xff0c;才会路由到具体服务。SpirnngCloudGateway由路由断言工厂实现&#xff0c;直接配置即生效&#xff0c;当然也支持自定义路由断言工厂。 内置路由断言工厂实现 ​ SpringClo…...

编程日记 2023/9/3 6:01:05

调用chat-gpt

调用chat-gpt 依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-web</artifactId></dependency><dependency><groupId>org.springframework.boot</groupId><artifact…...

编程日记 2023/9/3 6:00:02

Element组件浅尝辄止6：Dialog 对话框组件

Dialog 对话框组件&#xff1a;在保留当前页面状态的情况下&#xff0c;告知用户并承载相关操作。 大白话就是弹窗组件&#xff0c;日常开发中比较常见 1.怎样使用&#xff1f; //触发方式 <el-button type"text" click"dialogVisible true">打开&…...

编程日记 2023/9/3 5:59:01

Bert和LSTM：情绪分类中的表现

一、说明 这篇文章的目的是评估和比较 2 种深度学习算法&#xff08;BERT 和 LSTM&#xff09;在情感分析中进行二元分类的性能。评估将侧重于两个关键指标&#xff1a;准确性&#xff08;衡量整体分类性能&#xff09;和训练时间&#xff08;评估每种算法的效率&#xff09;。…...

编程日记 2023/9/3 5:58:00

【面试经典150题】跳跃游戏

题目链接 给你一个非负整数数组 nums &#xff0c;你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。 判断你是否能够到达最后一个下标&#xff0c;如果可以&#xff0c;返回 true &#xff1b;否则&#xff0c;返回 false 。 1 < nums…...

编程日记 2023/9/3 5:56:58

【Rust】003-基础语法：流程控制

【Rust】003-基础语法&#xff1a;流程控制 文章目录 【Rust】003-基础语法&#xff1a;流程控制一、概述二、if 表达式1、语法格式2、多个3、获取表达式的值 三、循环1、loop&#xff1a;无限循环&#xff0c;可跳出无限循环跳出循环返回值 2、while&#xff1a;条件循环&…...

编程日记 2023/9/3 5:55:58

0829【综述】面向时空数据的区块链研究综述

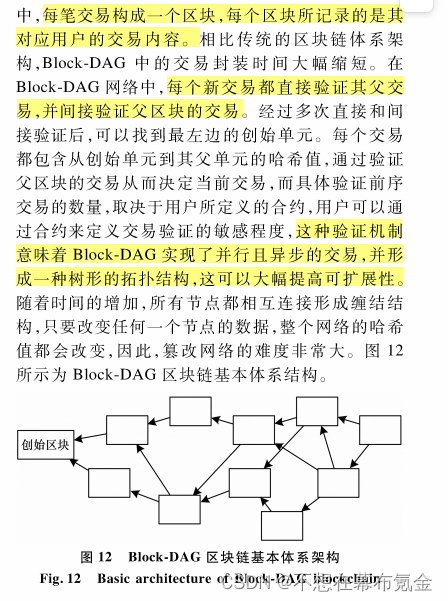
摘要:时空数据包括时间和空间2个维度,常被应用于物流、供应链等领域。传统的集中式存储方式虽然具有一定的便捷性,但不能充分满足时空数据存储及查询等要求,而区块链技术采用去中心化的分布式存储机制,并通过共识协议来保证数据的安全性。研究现有区块链1.0、2.0和以Block-DAG为…...

编程日记 2023/9/3 5:54:57

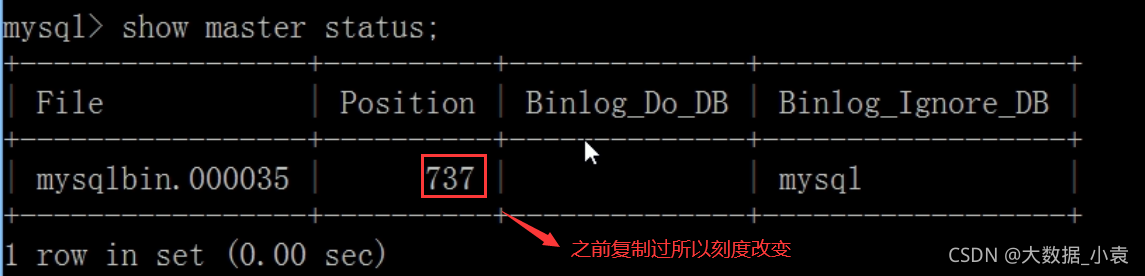
MySQL高级篇（SQL优化、索引优化、锁机制、主从复制）

目录 0 存储引擎介绍1 SQL性能分析2 常见通用的JOIN查询 SQL执行加载顺序七种JOIN写法3 索引介绍 3.1 索引是什么3.2 索引优劣势3.3 索引分类和建索引命令语句3.4 索引结构与检索原理3.5 哪些情况适合建索引3.6 哪些情况不适合建索引4 性能分析 4.1 性能分析前提知识4.2 Expla…...

编程日记 2023/9/3 5:53:54

YOLOV8模型使用-检测-物体追踪

这个最新的物体检测模型&#xff0c;很厉害的样子&#xff0c;还有物体追踪的功能。 有官方的Python代码&#xff0c;直接上手试试就好&#xff0c;至于理论&#xff0c;有想研究在看论文了╮(╯_╰)╭ 简单介绍 YOLOv8 中可用的模型 YOLOv8 模型的每个类别中有五个模型用于检…...

编程日记 2023/9/3 5:52:53

springmvc：设置后端响应给前端的json数据转换成String格式

设置spring-mvc.xml: xml <?xml version"1.0" encoding"UTF-8"?> <beans xmlns"http://www.springframework.org/schema/beans"xmlns:context"http://www.springframework.org/schema/context"xmlns:xsi"http://www.w…...

编程日记 2023/9/3 5:51:52

Mac安装brew、mysql、redis

mac安装brew mac安装brewmac安装mysql并配置开机启动mac安装redis并配置开机启动 mac安装brew 第一步&#xff1a;执行. /bin/bash -c "$(curl -fsSL https://raw.githubusercontent.com/Homebrew/install/HEAD/install.sh)"第二步&#xff1a;输入开机密码 第三…...

编程日记 2023/9/3 5:50:51

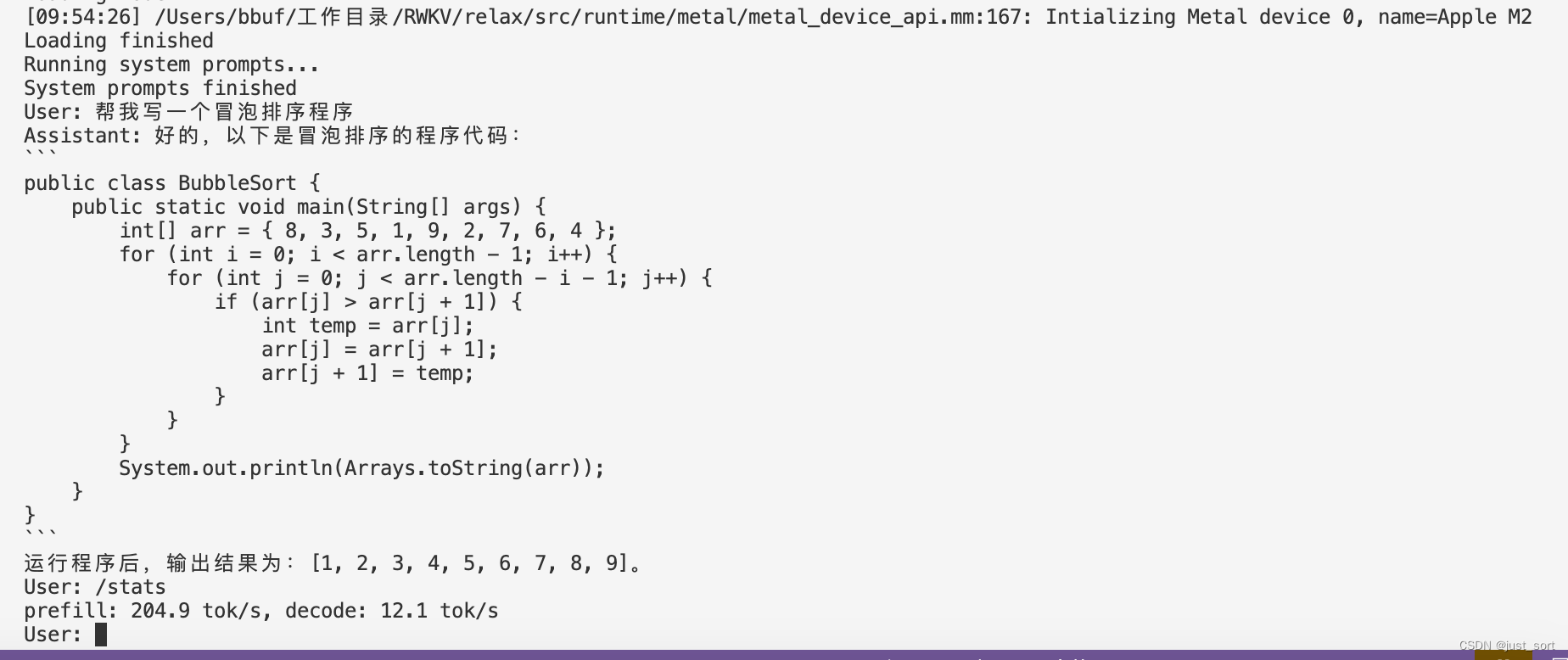
MLC-LLM 部署RWKV World系列模型实战（3B模型Mac M2解码可达26tokens/s）

0x0. 前言 我的 ChatRWKV 学习笔记和使用指南 这篇文章是学习RWKV的第一步&#xff0c;然后学习了一下之后决定自己应该做一些什么。所以就在RWKV社区看到了这个将RWKV World系列模型通过MLC-LLM部署在各种硬件平台的需求&#xff0c;然后我就开始了解MLC-LLM的编译部署流程和…...

编程日记 2023/9/3 5:49:49

Unity 之 参数类型之值类型参数的用法

文章目录 基本数据类型结构体结构体的进一步补充 总结&#xff1a; 当谈论值类型参数时&#xff0c;我们可以从基本数据类型和结构体两个方面详细解释。值类型参数指的是以值的形式传递给函数或方法的数据&#xff0c;而不是引用。 基本数据类型 基本数据类型的值类型参数&…...

编程日记 2023/9/3 5:48:48

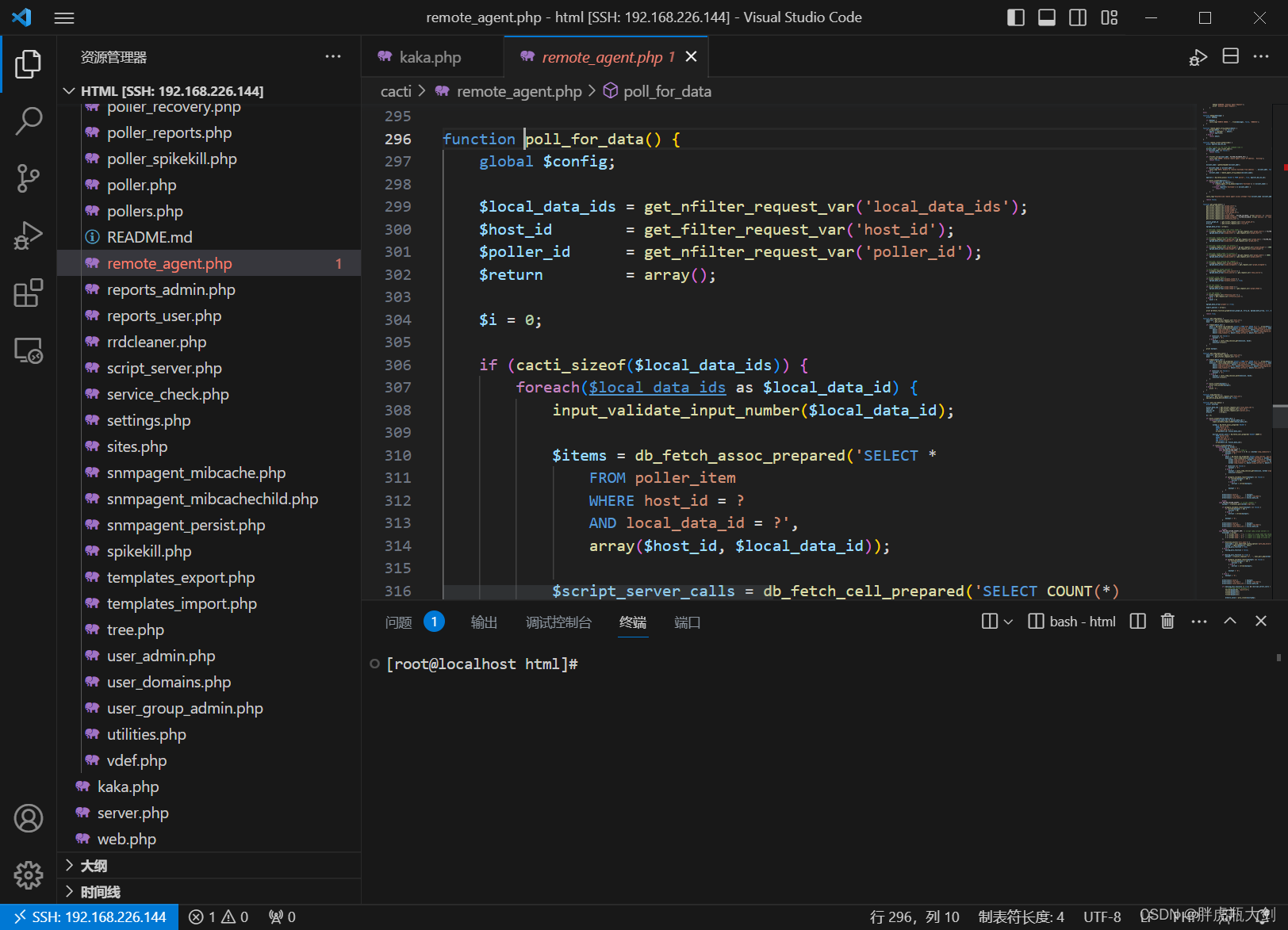
VScode远程连接主机

一、前期准备 1、Windows安装VSCode&#xff1b; 2、在VSCode中安装PHP Debug插件&#xff1b; 3、安装好Docker 4、在容器中安装Xdebug ①写一个展现phpinfo的php文件 <?php phpinfo(); ?>②在浏览器上打开该文件 ③复制所有信息丢到Xdebug: Installation instr…...

编程日记 2023/9/3 5:47:47

【iOS】属性关键字

文章目录 前言一、深拷贝与浅拷贝1、OC的拷贝方式有哪些2. OC对象实现的copy和mutableCopy分别为浅拷贝还是深拷贝&#xff1f;3. 自定义对象实现的copy和mutableCopy分别为浅拷贝还是深拷贝&#xff1f;4. 判断当前的深拷贝的类型&#xff1f;(区别是单层深拷贝还是完全深拷贝…...

编程日记 2023/9/3 5:46:46

Java 语言特性(面试系列2)

一、SQL 基础 1. 复杂查询 &#xff08;1&#xff09;连接查询&#xff08;JOIN&#xff09; 内连接&#xff08;INNER JOIN&#xff09;&#xff1a;返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

编程新知 2025/10/24 14:20:29

深入剖析AI大模型：大模型时代的 Prompt 工程全解析

今天聊的内容&#xff0c;我认为是AI开发里面非常重要的内容。它在AI开发里无处不在&#xff0c;当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗"&#xff0c;或者让翻译模型 "将这段合同翻译成商务日语" 时&#xff0c;输入的这句话就是 Prompt。…...

编程新知 2026/2/8 20:42:53

Linux 文件类型，目录与路径，文件与目录管理

文件类型 后面的字符表示文件类型标志 普通文件&#xff1a;-&#xff08;纯文本文件&#xff0c;二进制文件&#xff0c;数据格式文件&#xff09; 如文本文件、图片、程序文件等。 目录文件&#xff1a;d&#xff08;directory&#xff09; 用来存放其他文件或子目录。 设备…...

编程新知 2026/2/8 20:42:46

反向工程与模型迁移：打造未来商品详情API的可持续创新体系

在电商行业蓬勃发展的当下&#xff0c;商品详情API作为连接电商平台与开发者、商家及用户的关键纽带&#xff0c;其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息&#xff08;如名称、价格、库存等&#xff09;的获取与展示&#xff0c;已难以满足市场对个性化、智能…...

编程新知 2025/9/15 5:56:53

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能

下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能&#xff0c;包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

编程新知 2025/11/14 9:31:35

Oracle查询表空间大小

1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

编程新知 2025/11/8 0:24:13

循环冗余码校验CRC码 算法步骤+详细实例计算

通信过程&#xff1a;&#xff08;白话解释&#xff09; 我们将原始待发送的消息称为 M M M&#xff0c;依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)&#xff08;意思就是 G &#xff08; x ) G&#xff08;x) G&#xff08;x) 是已知的&#xff09;&#xff0…...

编程新知 2026/2/9 21:57:29

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码： prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

编程新知 2025/7/4 0:50:01

安卓基础（aar）

重新设置java21的环境&#xff0c;临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的&#xff1a; MyApp/ ├── app/ …...

编程新知 2026/1/25 8:10:56

NXP S32K146 T-Box 携手 SD NAND（贴片式TF卡）：驱动汽车智能革新的黄金组合

在汽车智能化的汹涌浪潮中&#xff0c;车辆不再仅仅是传统的交通工具&#xff0c;而是逐步演变为高度智能的移动终端。这一转变的核心支撑&#xff0c;来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒&#xff08;T-Box&#xff09;方案&#xff1a;NXP S32K146 与…...

编程新知 2026/1/24 14:43:35