数学建模之灰色预测
灰色预测(Grey Forecasting)是一种用于时间序列数据分析和预测的方法,通常用于处理具有较少历史数据的情况或者数据不够充分的情况。它是一种非常简单但有效的方法,基于灰色系统理论,用来估计未来的趋势。
以下是灰色预测的基本思想和步骤:
-
建立灰色模型:首先,需要建立一个灰色模型,通常使用一些已知的历史数据。灰色模型可以是一阶、二阶等,具体的模型选择取决于数据的性质和趋势。最常用的是一阶指数灰色模型(GM(1,1))。
-
数据预处理:对原始数据进行累加运算,将原始数据序列转化为累加生成数据序列。
-
建立灰色微分方程:使用累加生成数据序列,建立灰色微分方程,然后求解微分方程的参数。
-
模型检验:对模型进行检验,检查模型拟合的程度以及预测精度。可以使用残差分析等方法来检验模型。
-
预测未来:使用建立的模型来进行未来的预测。
灰色预测方法的优点是不需要大量的历史数据,适用于小样本数据和短期预测。然而,它也有一些限制,如对数据质量要求较高,无法处理非线性关系等。
灰色预测是一种在某些情况下非常有用的时间序列分析方法,特别是在数据有限或者数据质量较差的情况下,可以作为一种可选的预测工具。
灰色预测的示例代码如下。这里使用一阶指数灰色模型(GM(1,1))来对一组示例数据进行预测。
#include <iostream>
#include <vector>
#include <cmath>// 灰色预测的一阶指数灰色模型
void greyPrediction(const std::vector<double>& data, double& a, double& b) {int n = data.size();// 累加生成序列std::vector<double> sumData(n, 0.0);for (int i = 0; i < n; ++i) {for (int j = 0; j <= i; ++j) {sumData[i] += data[j];}}// 计算累加生成数据的一次差分序列std::vector<double> diffData(n - 1, 0.0);for (int i = 0; i < n - 1; ++i) {diffData[i] = sumData[i] + sumData[i + 1] / 2.0;}// 建立灰色微分方程double X0 = data[0];double B = 0.0;for (int i = 0; i < n - 1; ++i) {B += -2 * (X0 + B / 2.0 - diffData[i]) / (n - 1);}// 计算参数 a 和 ba = X0;b = B;
}int main() {// 示例数据std::vector<double> data = {45, 55, 67, 80, 92, 103};// 预测未来两个时间点的值double a, b;greyPrediction(data, a, b);double nextValue = a + b;double nextNextValue = a + 2 * b;std::cout << "Predicted next value: " << nextValue << std::endl;std::cout << "Predicted value after that: " << nextNextValue << std::endl;return 0;
}
在这个示例中,我们使用了一组示例数据 data,然后通过 greyPrediction 函数建立了一阶指数灰色模型,预测了未来两个时间点的值。这个示例只是一个简单的演示,实际应用中,您需要根据具体问题和数据来调整模型和参数。请注意,灰色预测方法通常需要更多的数据点来获得更准确的预测结果。
以下是使用 Python 进行灰色预测的示例代码。在这个示例中,我们将使用一阶指数灰色模型(GM(1,1))来对一组示例数据进行预测。
import numpy as np# 灰色预测的一阶指数灰色模型
def greyPrediction(data):n = len(data)# 累加生成序列sumData = np.cumsum(data)# 计算累加生成数据的一次差分序列diffData = np.zeros(n-1)for i in range(n-1):diffData[i] = sumData[i] + sumData[i+1] / 2.0# 建立灰色微分方程X0 = data[0]B = 0.0for i in range(n-1):B += -2 * (X0 + B / 2.0 - diffData[i]) / (n - 1)# 计算参数 a 和 ba = X0b = Breturn a, b# 示例数据
data = [45, 55, 67, 80, 92, 103]# 预测未来两个时间点的值
a, b = greyPrediction(data)
nextValue = a + b
nextNextValue = a + 2 * bprint("Predicted next value:", nextValue)
print("Predicted value after that:", nextNextValue)
在这个 Python 示例中,我们使用 NumPy 库来进行数组运算。首先,我们定义了 greyPrediction 函数来建立一阶指数灰色模型并预测未来两个时间点的值。然后,我们提供了示例数据 data,并打印出预测的结果。
相关文章:

数学建模之灰色预测
灰色预测(Grey Forecasting)是一种用于时间序列数据分析和预测的方法,通常用于处理具有较少历史数据的情况或者数据不够充分的情况。它是一种非常简单但有效的方法,基于灰色系统理论,用来估计未来的趋势。 以下是灰色…...

03_nodejd_npm install报错
npm install报错 npm ERR! code ERESOLVE npm ERR! ERESOLVE unable to resolve dependency tree npm ERR! npm ERR! While resolving: 5kcrm11.0.0 npm ERR! Found: vue2.5.17 npm ERR! node_modules/vue npm ERR! vue"2.5.17" from the root project npm ERR! np…...

three.js(二):webpack + three.js + ts
用webpackts 开发 three.js 项目 webpack 依旧是主流的模块打包工具;ts和three.js 是绝配,three.js本身就是用ts写的,ts可以为three 项目提前做好规则约束,使项目的开发更加顺畅。 1.创建一个目录,初始化 npm mkdir demo cd de…...
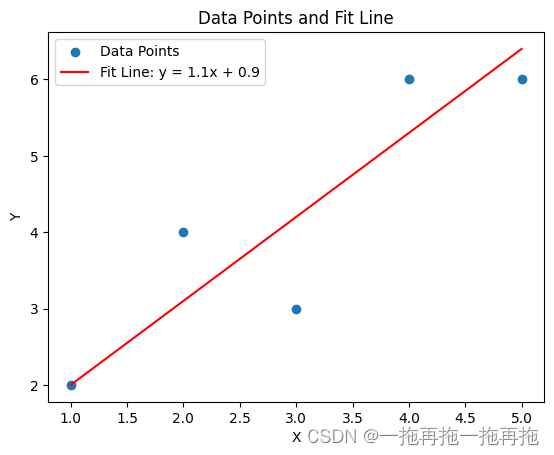
最小二乘法处理线性回归
最小二乘法是一种数学优化技术,用于查找最适合一组数据点的函数。 该方法主要用于线性回归分析,当然,也可用于非线性问题。 开始之前,我们先理解一下什么是回归。 回归:回归是一种监督学习算法,用于建模和…...

ModbusCRC16校验 示例代码
作者: Herman Ye Galbot Auromix 测试环境: Ubuntu20.04 更新日期: 2023/08/30 注1: Auromix 是一个机器人爱好者开源组织。 注2: 本文在更新日期经过测试,确认有效。 笔者出于学习交流目的, 给…...

一不留神就掉坑
乘除顺序问题 在据卡特兰数[1]公式,解决leetcode-96 不同的二叉搜索树[2]时,遇到一个非常诡异的问题, package mainimport "fmt"func main() { for i : 0; i < 40; i { fmt.Printf("第%d个卡特兰数为:%d\n", i, numTrees(i)) }}func numTrees(n int) i…...

Redis数据类型(list\set\zset)
"maybe its why" List类型 列表类型是⽤来存储多个有序的字符串,列表中的每个字符串称为元素(element),⼀个列表最多可以存储个2^32 - 1个元素。在Redis中,可以对列表两端插⼊(push)…...

TongWeb安装以及集成
TongWeb 安装步骤 静默安装 获取linux可执行安装包 如: Install_TWx.x.x.x_Enterprise_Linux.bin 创建安装所需配置文件 install.properties 内容如下 [root@node5 tongweb]# cat install.properties INSTALL_UI=silent USER_INSTALL_DIR=/home/tongweb SILENT_JDK_HOME=/jd…...
ScreenToGif-动图制作软件实用操作
ScreenToGif官网:ScreenToGif ⭕第一步:启动页面 ⭕第二步:选项 🥝录像机-捕获频率选择手动-播放延迟1000ms(可以任意) ⭕第三步:录像机开始录屏 🥝我们调整录屏的大小后,打开画图,…...

sqlibs安装及复现
sqlibs安装 安装phpstudy后,到github上获取sqlibs源码 sqli-labs项目地址—Github获取:GitHub - Audi-1/sqli-labs: SQLI labs to test error based, Blind boolean based, Time based. 在phpstudy本地文件中的Apache目录中解压上方下载的源码。 将sq…...

OpenAI 创始人 Sam Altman 博客有一篇 10 年前的文章
OpenAI 创始人 Sam Altman 博客有一篇 10 年前的文章《Advice for ambitious 19 year olds》,给 19 岁年轻人的建议,从 #参考答案 看到,非常适合我们🤣年轻人,顺便用 GPT4 重新翻译了下全文。 太长不读纯摘要版本如下&…...
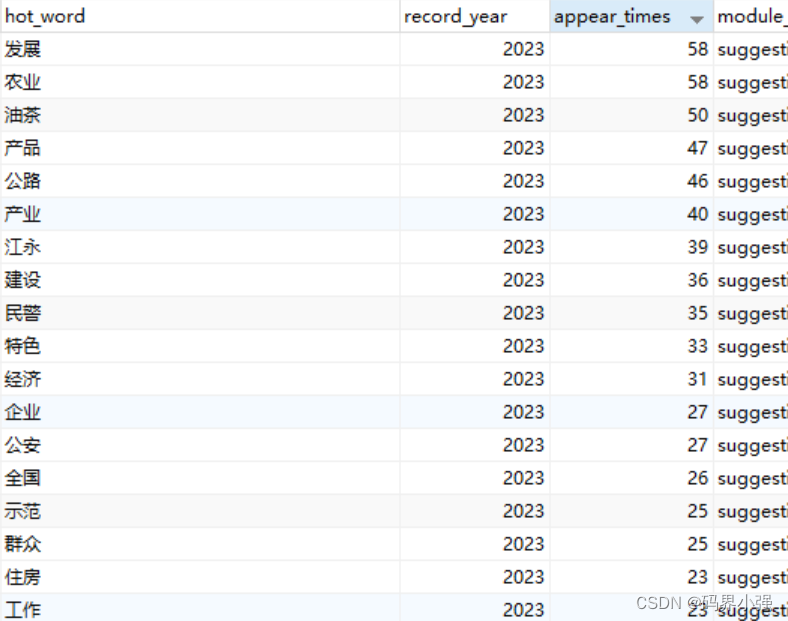
写的一款简易的热点词汇记录工具
项目需要对用户提交的附件、文章、搜索框内容等做热词分析。如下图: 公司有大数据团队。本着不麻烦别人就不麻烦别人的原则,写了一款简易的记录工具,原理也简单,手工在业务插入锚点,用分词器分好词,排掉字…...
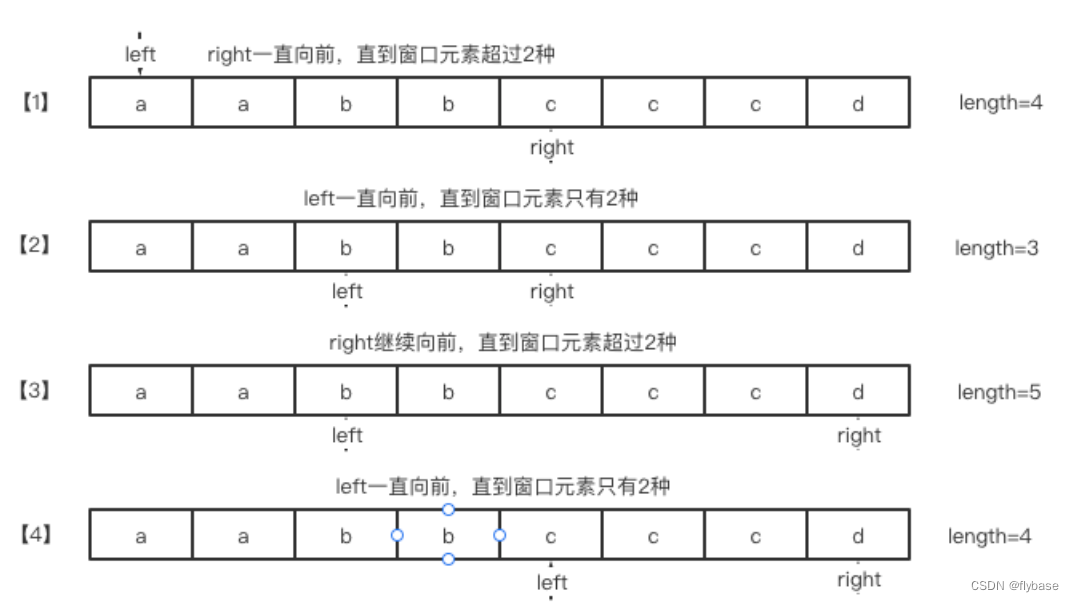
算法通关村——滑动窗口高频问题
1. 无重复字符的最长子串 给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。 示例 1: 输入: s “abcabcbb” 输出: 3 解释: 因为无重复字符的最长子串是 “abc”,所以其长度为 3。 1.1 滑动窗口 找到最长字串需要找到字串的首尾位置…...
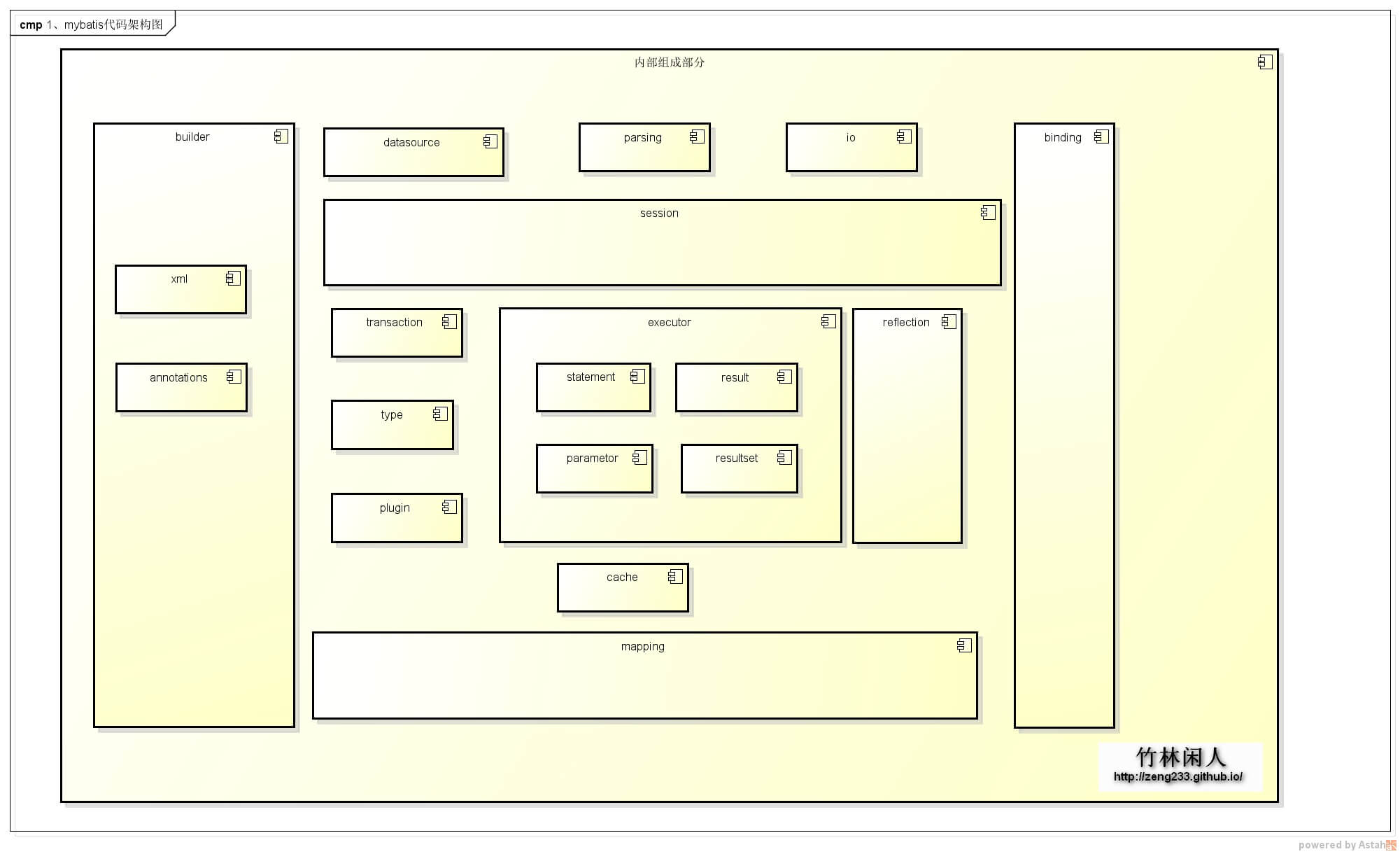
mybatis源码学习-2-项目结构
写在前面,这里会有很多借鉴的内容,有以下三个原因 本博客只是作为本人学习记录并用以分享,并不是专业的技术型博客笔者是位刚刚开始尝试阅读源码的人,对源码的阅读流程乃至整体架构并不熟悉,观看他人博客可以帮助我快速入门如果只是笔者自己观看,难免会有很多弄不懂乃至理解错误…...

selenium 自动化测试——环境搭建
安装python,并且使用pip命令安装 selenium pip3 install selenium 然后尝试第一次使用selenium 完成一个简单的测试自动化脚本 from selenium import webdriver from selenium.webdriver.common.by import By import timedriver webdriver.Chrome() driver.get(…...

得物一面,场景题问得有点多!
题目来源:https://www.nowcoder.com/discuss/525371909735792640 前文 本期是【捞捞面经】系列文章的第 1 期,持续更新中…。 《捞捞面经》系列正式开始连载啦,据说看了这个系列的朋友都拿到了大厂offer~ 欢迎星标订阅,持续更新…...

Prompt Tuning 和instruct tuning
Prompt Tuning 是啥? prompt的思想是,把下游任务的输入转化为预训练模型的原始任务。 以bert作为举例,假设任务是文本分类。“今天天气很好。”我们想判断一下这句话的情感是正面还是负面 fine-tune的方法是在bert之后接一个head࿰…...

springboot 与异步任务,定时任务,邮件任务
异步任务 在Java应用中,绝大多数情况下都是通过同步的方式来实现交互处理的;但是在处理与第三方系统交互的时候,容易造成响应迟缓的情况,之前大部分都是使用多线程来完成此类任务,其实,在Spring 3.x之后&a…...

2022年06月 C/C++(六级)真题解析#中国电子学会#全国青少年软件编程等级考试
C/C++编程(1~8级)全部真题・点这里 第1题:小白鼠再排队2 N只小白鼠(1 < N < 100),每只鼠头上戴着一顶有颜色的帽子。现在称出每只白鼠的重量,要求按照白鼠重量从小到大的顺序输出它们头上帽子的颜色。帽子的颜色用 “red”,“blue”等字符串来表示。不同的小白鼠可…...

【C++】C++11新特性(下)
上篇文章(C11的新特性(上))我们讲述了C11中的部分重要特性。本篇接着上篇文章进行讲解。本篇文章主要进行讲解:完美转发、新类的功能、可变参数模板、lambda 表达式、包装器。希望本篇文章会对你有所帮助。 文章目录 一…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...
