论文阅读_扩散模型_DM
英文名称: Deep Unsupervised Learning using Nonequilibrium Thermodynamics
中文名称: 使用非平衡热力学原理的深度无监督学习
论文地址: http://arxiv.org/abs/1503.03585
代码地址: https://github.com/Sohl-Dickstein/Diffusion-Probabilistic-Models
时间: 2015-11-18
作者: Jascha Sohl-Dickstein, 斯坦福大学
引用量: 1813
读后感
论文目标是建立灵活且易用的数据生成模型。它利用非平衡统计物理学原理:通过扩散过程(少量加噪)系统地、缓慢地破坏数据分布中的结构;然后,学习反向扩散过程,恢复数据结构。
介绍
扩散模型与变分模型
扩散模型与变分模型原理类似,都是将图片拆成一系列高斯分布的均值和方差,而扩散模型是一个逐步变化的过程,主要差别如下:
- 原理不同:扩散模型使用物理学、准静态过程和退火采样的思想。由于任何平滑目标分布都存在扩散过程,因此理论上该方法可以捕获任意形式的数据分布。
- 展示了用简单的乘法,将一个分布逐步转换为另一分布的过程。
- 解决了推理模型和生成模型之间目标的不对称性,将正向(推理)过程限制为简单的函数形式,反向(生成)过程将具有相同的函数形式。
- 可训练具有数**千层(时间步)**的模型。
- 精细控制每层中熵产生的上限和下限。
方法

请记住图中这些符号,很多后续文章都延用了这些符号的定义。
向前轨迹
其中蓝色是扩散过程,从左往右看,总共T步,每步加一点高斯噪声,将瑞士卷图扩散成了高斯分布,扩展过程设为q。每步都根据上一步数据而来:
q ( x ( 0 ⋯ T ) ) = q ( x ( 0 ) ) ∏ t = 1 T q ( x ( t ) ∣ x ( t − 1 ) ) q\left(\mathbf{x}^{(0 \cdots T)}\right)=q\left(\mathbf{x}^{(0)}\right) \prod_{t=1}^{T} q\left(\mathbf{x}^{(t)} \mid \mathbf{x}^{(t-1)}\right) q(x(0⋯T))=q(x(0))t=1∏Tq(x(t)∣x(t−1))
反向轨迹
中间红色部分是扩散的逆过程,从右往左看,图片逐步恢复,恢复过程设为p;在训练过程中,通过学习高斯扩散的逆过程,使数据转换回原分布,从而生成数据。
p ( x ( 0 ⋯ T ) ) = p ( x ( T ) ) ∏ t = 1 T p ( x ( t − 1 ) ∣ x ( t ) ) p\left(\mathbf{x}^{(0 \cdots T)}\right)=p\left(\mathbf{x}^{(T)}\right) \prod_{t=1}^{T} p\left(\mathbf{x}^{(t-1)} \mid \mathbf{x}^{(t)}\right) p(x(0⋯T))=p(x(T))t=1∏Tp(x(t−1)∣x(t))
最后一行展示了反向扩散过程的漂移项。fμ (x(t), t) 是高斯逆马尔可夫转移的均值和协方差的函数。
扩散的原理是通过马尔可夫链逐渐将一种分布转换为另一种分布。最终,估计概率分布的任务简化为对高斯序列的均值和协方差函数的回归任务(这里的0状态指的是原始图,T状态指高斯分布图);由于扩散链中的每个步骤都具有可分析评估的概率(对比正向和反向变化中每一步数据的相似度),因此也可以对整个链进行分析评估。
模型概率
计算将图像恢复成原图的概率,可拆解成每一步变化的累积。
p ( x ( 0 ) ) = ∫ d x ( 1 ⋯ T ) p ( x ( 0 ⋯ T ) ) q ( x ( 1 ⋯ T ) ∣ x ( 0 ) ) q ( x ( 1 ⋯ T ) ∣ x ( 0 ) ) = ∫ d x ( 1 ⋯ T ) q ( x ( 1 ⋯ T ) ∣ x ( 0 ) ) p ( x ( 0 ⋯ T ) ) q ( x ( 1 ⋯ T ) ∣ x ( 0 ) ) = ∫ d x ( 1 ⋯ T ) q ( x ( 1 ⋯ T ) ∣ x ( 0 ) ) p ( x ( T ) ) ∏ t = 1 T p ( x ( t − 1 ) ∣ x ( t ) ) q ( x ( t ) ∣ x ( t − 1 ) ) \begin{aligned} p\left(\mathbf{x}^{(0)}\right)= & \int d \mathbf{x}^{(1 \cdots T)} p\left(\mathbf{x}^{(0 \cdots T)}\right) \frac{q\left(\mathbf{x}^{(1 \cdots T)} \mid \mathbf{x}^{(0)}\right)}{q\left(\mathbf{x}^{(1 \cdots T)} \mid \mathbf{x}^{(0)}\right)} \\ = & \int d \mathbf{x}^{(1 \cdots T)} q\left(\mathbf{x}^{(1 \cdots T)} \mid \mathbf{x}^{(0)}\right) \frac{p\left(\mathbf{x}^{(0 \cdots T)}\right)}{q\left(\mathbf{x}^{(1 \cdots T)} \mid \mathbf{x}^{(0)}\right)} \\ = & \int d \mathbf{x}^{(1 \cdots T)} q\left(\mathbf{x}^{(1 \cdots T)} \mid \mathbf{x}^{(0)}\right) \\ & p\left(\mathbf{x}^{(T)}\right) \prod_{t=1}^{T} \frac{p\left(\mathbf{x}^{(t-1)} \mid \mathbf{x}^{(t)}\right)}{q\left(\mathbf{x}^{(t)} \mid \mathbf{x}^{(t-1)}\right)} \end{aligned} p(x(0))===∫dx(1⋯T)p(x(0⋯T))q(x(1⋯T)∣x(0))q(x(1⋯T)∣x(0))∫dx(1⋯T)q(x(1⋯T)∣x(0))q(x(1⋯T)∣x(0))p(x(0⋯T))∫dx(1⋯T)q(x(1⋯T)∣x(0))p(x(T))t=1∏Tq(x(t)∣x(t−1))p(x(t−1)∣x(t))
训练
具体方法是计算熵 H 和 KL 散度。其推导与变分贝叶斯方法中对数似然界限的推导类似。DK散度描述了每一时间步数据分布的差异,熵描述了数据的混乱程度。
L ≥ K K = − ∑ t = 2 T ∫ d x ( 0 ) d x ( t ) q ( x ( 0 ) , x ( t ) ) . D K L ( q ( x ( t − 1 ) ∣ x ( t ) , x ( 0 ) ) ∥ p ( x ( t − 1 ) ∣ x ( t ) ) ) + H q ( X ( T ) ∣ X ( 0 ) ) − H q ( X ( 1 ) ∣ X ( 0 ) ) − H p ( X ( T ) ) . \begin{aligned} L & \geq K \\ K= & -\sum_{t=2}^{T} \int d \mathbf{x}^{(0)} d \mathbf{x}^{(t)} q\left(\mathbf{x}^{(0)}, \mathbf{x}^{(t)}\right) . \\ & D_{K L}\left(q\left(\mathbf{x}^{(t-1)} \mid \mathbf{x}^{(t)}, \mathbf{x}^{(0)}\right) \| p\left(\mathbf{x}^{(t-1)} \mid \mathbf{x}^{(t)}\right)\right) \\ & +H_{q}\left(\mathbf{X}^{(T)} \mid \mathbf{X}^{(0)}\right)-H_{q}\left(\mathbf{X}^{(1)} \mid \mathbf{X}^{(0)}\right)-H_{p}\left(\mathbf{X}^{(T)}\right) . \end{aligned} LK=≥K−t=2∑T∫dx(0)dx(t)q(x(0),x(t)).DKL(q(x(t−1)∣x(t),x(0))∥p(x(t−1)∣x(t)))+Hq(X(T)∣X(0))−Hq(X(1)∣X(0))−Hp(X(T)).
设置扩散率 βt
热力学中,在平衡分布之间移动时所采取的时间表决定了损失多少自由能。简单地说,就是如何设置每一步变化的大小。一般情况下,第一步β设成一个很小的常数,以防过拟合,然后2-T步逐步扩大。将在之后的DDPM中详述。
乘以分布计算后验
对大多数模型而言,乘以分布计算量大,而在扩散模型中则比较简单,第二个分布可以被视为扩散过程中每个步骤的小扰动。
相关文章:

论文阅读_扩散模型_DM
英文名称: Deep Unsupervised Learning using Nonequilibrium Thermodynamics 中文名称: 使用非平衡热力学原理的深度无监督学习 论文地址: http://arxiv.org/abs/1503.03585 代码地址: https://github.com/Sohl-Dickstein/Diffusion-Probabilistic-Models 时间: 2015-11-18 作…...
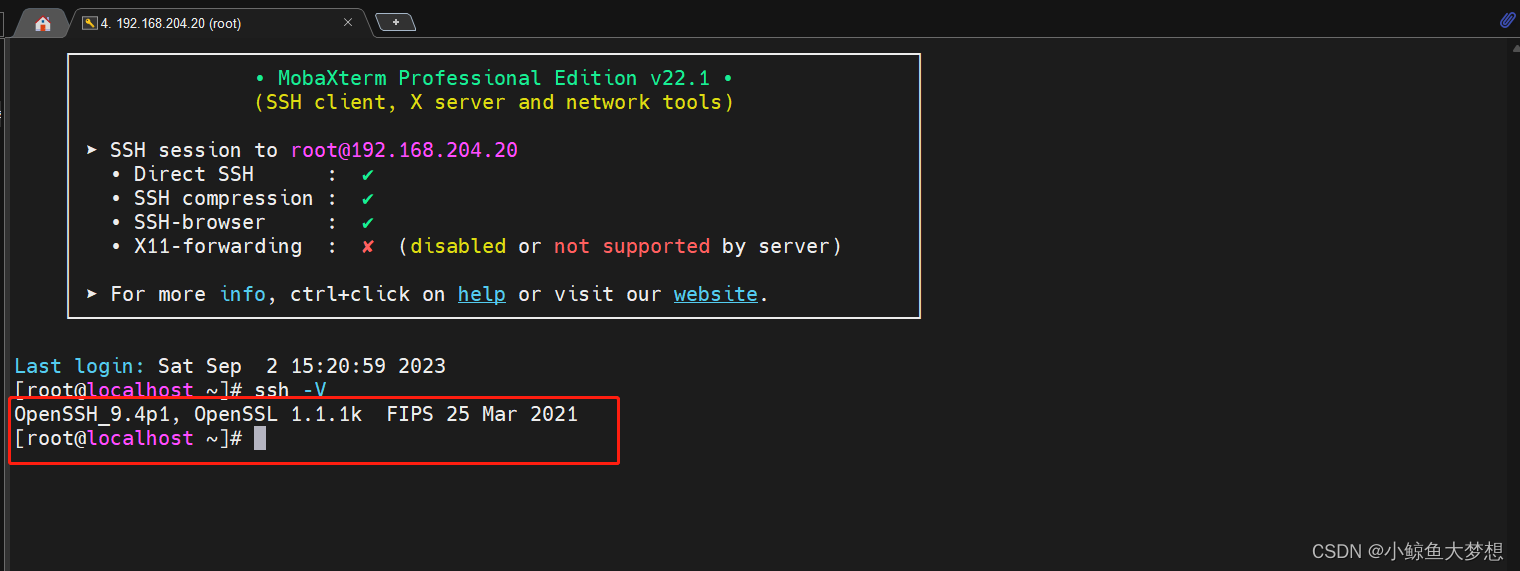
【每日运维】RockyLinux8.6升级OpenSSH9.4p1
为什么需要升级openssh呢,因为很多项目进行漏扫结果都会涉及到这个服务器核心组件,一想到以前升级openssh带来的各种依赖性问题就头疼,不管是什么发行版,升级这个东西真的很烦,这次发现可能还会有好一点的通用一点的升…...
)
libdrm全解析三十八 —— 源码全解析(35)
接前一篇文章:libdrm全解析三十七 —— 源码全解析(34) 本文参考以下博文: DRM 驱动程序开发(VKMS) 特此致谢! 前一篇文章讲解完了drmModeSetCrtc(crtc_id, fb_id, connector_id, mode)&#…...

jar包和war包的区别
SpringBoot项目既可以打成war包发布,也可以找成jar包发布。 jar包 jar包:直接通过内置Tomcat运行,不需要额外安装Tomcat。如需修改内置Tomcat的配置,只需要在SpringBoot的配置文件中配置。内置Tomcat没有自己的日志输出࿰…...
——点云投影到平面)
CloudCompare 二次开发(10)——点云投影到平面
目录 一、概述二、代码集成三、结果展示一、概述 不依赖任何第三方点云相关库,使用CloudCompare编程实现点云投影到指定平面,具体计算原理见:PCL 点云投影到拟合平面 二、代码集成 1、mainwindow.h文件public中添加: void doActionProjectToPlane(); // 投影到平面2、…...
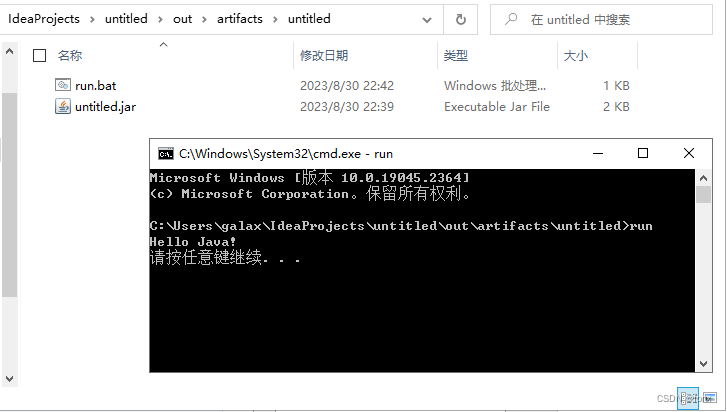
如何制作并运行 jar 程序
以下是用 Intellij 制作 jar 程序,并运行的方法。 【1】新建工程,保持默认选项,Next 【2】保持默认选项,Next 【3】给工程命名,设置保存位置,Finish 【4】新建工程结束,进入开发界面 【5】展开…...

Hadoop MapReduce 调优参数
文章目录 MapReduce 调优参数详解MapReduce 调优参数一键复制 前言: 下列参数基于 hadoop v3.1.3 版本,共三台服务器,配置都为 4 核,4G 内存。 MapReduce 调优参数详解 这个参数定义了在 Reduce 阶段同时进行的拷贝操作的数量&…...

springboot 与 Redis整合
SpringBoot 操作数据:Spring-data jpa jdbc mongodb redis! SpringData 也是和SpringBoot 齐名的项目! 说明:在SpringBoot2.X 之后,原来使用的jedis被替换成了lettuce jedis: 采用的直连,多个线程操作的话&…...

如何高效地设计测试用例并评审
编写出好的测试用例是每一个测试工程师的职责,但在实际工作中大家写的测试用例往往需要不断地修改才能使用,这不仅浪费了时间,还容易让测试工程师产生自我否定的情绪,甚至在团队中产生各种矛盾。 那如何高效地设计测试用例呢&…...

基于python+Django知识图谱的医疗问答系统设计与实现
摘 要 从信息技术的发展至今,各色各样的技术能够满足各类人群的需求,能够让各种业务行业的痛点变成能够可以解决的方法,随着我们经济的不断提高,越来越多的人都该关注健康,那么健康饮食、健康医疗是我们生活中所追求的…...

cuda编程常见问题
cuda环境配置 参考链接 https://blog.csdn.net/weixin_43788327/article/details/125823507?spm1001.2014.3001.5506 疑难问题 在学习《GPU高性能编程CUDA实战》这本书时,发现书里面的代码很多变量都没定义过,经过搜索发现这都是书上自带的代码。 代…...

QTday3
作业1:通过对话框实现保存文件 void burger::on_saveBtn_clicked() {//调用函数,获取文件路径QString filename QFileDialog::getSaveFileName(this,"选择文件夹","./","Text File(*.txt)");if(filename.isNull()){QMes…...

docker镜像是如何导入的?
镜像导入是由image/tarexport/load.go#tarexporter.Load()完成的 以下代码参考github.com/docker/docker版本v0.0.0-20181129155816-baab736a3649 主要是注册镜像信息以及解包镜像tar流到新root 导出和保存的区别在于 导出(export): 仅导出文件结构保存(save): 保存镜像历史和元…...

四川大学874考研真题00-23
22, 2022年硕士学位研究生入学考试试题回忆版 数据结构 1.一个时间复杂度为n2 的算法运行,m1算n个问题用时1秒,m2处理器是m1效率的64倍,则m2每秒能计算()个问题。 A. 64n B. 8n …...

openGauss学习笔记-58 openGauss 高级特性-资源池化
文章目录 openGauss学习笔记-58 openGauss 高级特性-资源池化58.1 特性简介58.2 架构介绍58.3 功能特点58.4 适用场景与限制58.5 手动安装示例58.6 OCK RDMA使用示例58.7 OCK SCRLock使用示例 openGauss学习笔记-58 openGauss 高级特性-资源池化 58.1 特性简介 资源池化特性主…...

centos升级cmake之相关问题解决
1. yum安装(仓库默认版本) # 查看可安装版本 yum --showduplicates list xxxx# 安装指定版本 yum install xxxx-1.23.1 2. 安装高版本cmake 2.1 一开始下载的是cmake-xxx.zip,在 ./bootstrap 一直会报错“missing terminating " character”,后来…...

vcs仿真教程(查看断言)
VCS是在linux下面用来进行仿真看波形的工具,类似于windows下面的modelsim以及questasim等工具,以及quartus、vivado仿真的操作。 1.vcs的基本指令 vcs的常见指令后缀 sim常见指令 2.使用vcs的实例 (1)新建文件夹: …...

2023开学礼新疆石河子大学图书馆藏八一新书《乡村振兴战略下传统村落文化旅游设计》许少辉新财经理工
2023开学礼新疆石河子大学图书馆藏八一新书《乡村振兴战略下传统村落文化旅游设计》许少辉新财经理工...

javaee spring aop 切入点表达式
1、切入点表达式:对指定的方法进行拦截,并且生成代理表达式。 表达式语法:execution([修饰符] 返回值类型 包名.类名.方法名(参数))execution( public void com.test.service.impl.UsersService.add() )2、表达式不同写法 1.匹配指定方法 …...

js 获得元素的offsetLeft
要获得元素相对于其offsetParent元素左侧边缘的距离(即offsetLeft),可以使用如下代码: var el document.getElementById(your-element-id); var offsetLeft el.offsetLeft;其中,el为要获取offsetLeft的元素对象&…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...
