games101作业1
题目
给定三维下三个点 v0(2.0, 0.0, −2.0), v1(0.0, 2.0, −2.0), v2(−2.0, 0.0, −2.0), 你需要将这三个点的坐标变换为屏幕坐标并在屏幕上绘制出对应的线框三角形 (在代码框架中,我们已经提供了 draw_triangle 函数,所以你只需要去构建变换矩阵即可)。简而言之,我们需要进行模型、视图、投影、视口等变换来将三角形显示在屏幕上。在提供的代码框架中,我们留下了模型变换和投影变换的部分给你去完成。
题解
本次作业需要实现代码框架中的两个接口:
Eigen::Matrix4f get_model_matrix(float rotation_angle);
Eigen::Matrix4f get_projection_matrix(float eye_fov, float aspect_ratio,float zNear, float zFar);
1. 旋转
第一个接口相对比较简单,直接返回旋转矩阵即可。注意:需要将角度转为弧度。
绕Z轴旋转矩阵如下:
R z ( α ) = ( cos α − sin α 0 0 sin α cos α 0 0 0 0 1 0 0 0 0 1 ) \mathbf{R}_z(\alpha)=\left(\begin{array}{cccc} \cos \alpha & -\sin \alpha & 0 & 0 \\ \sin \alpha & \cos \alpha & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right) Rz(α)= cosαsinα00−sinαcosα0000100001
课程中还讲到了绕X 轴的旋转矩阵
R x ( α ) = ( 1 0 0 0 0 cos α − sin α 0 0 sin α cos α 0 0 0 0 1 ) \mathbf{R}_x(\alpha)=\left(\begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & \cos \alpha & -\sin \alpha & 0 \\ 0 & \sin \alpha & \cos \alpha & 0 \\ 0 & 0 & 0 & 1 \end{array}\right) Rx(α)= 10000cosαsinα00−sinαcosα00001
绕Y轴的旋转矩阵( 注意这里的sin符号和其他两种情况不同,是因为右手坐标系,从+x->+z旋转,Y轴和拇指方向相反)
R y ( α ) = ( cos α 0 sin α 0 0 1 0 0 − sin α 0 cos α 0 0 0 0 1 ) \mathbf{R}_y(\alpha)=\left(\begin{array}{cccc} \cos \alpha & 0 & \sin \alpha & 0 \\ 0 & 1 & 0 & 0 \\ -\sin \alpha & 0 & \cos \alpha & 0 \\ 0 & 0 & 0 & 1 \end{array}\right) Ry(α)= cosα0−sinα00100sinα0cosα00001
角度转为弧度:
α = θ π 180 \alpha=\theta \frac{\pi}{180} α=θ180π
2. 正交投影
根据课程中的推导过程:其中 z ∈ [ − 1 , 1 ] z \in[-1,1] z∈[−1,1],采用右手坐标系。观察变换完成后,将物体投影到相机坐标系中。然后在相机坐标系中进行投影变换:正交投影或者透视投影。正交投影的基本思想是:将长方体视窗体平移到原点,然后进行缩放,使得: x , y , z ∈ [ − 1 , 1 ] x,y,z \in[-1,1] x,y,z∈[−1,1]
假设长方体视窗体的左右上下前后六个面的坐标分别为: l , r , t , b , n , f l,r,t,b,n,f l,r,t,b,n,f. 正交投影矩阵如下:
M ortho = [ 2 r − l 0 0 0 0 2 t − b 0 0 0 0 2 n − f 0 0 0 0 1 ] [ 1 0 0 − r + l 2 0 1 0 − t + b 2 0 0 1 − n + f 2 0 0 0 1 ] = [ 2 r − l 0 0 − r + l r − l 0 2 t − b 0 − t + b t − b 0 0 2 n − f − n + f n − f 0 0 0 1 ] M_{\text {ortho }}=\left[\begin{array}{cccc} \frac{2}{r-l} & 0 & 0 & 0 \\ 0 & \frac{2}{t-b} & 0 & 0 \\ 0 & 0 & \frac{2}{n-f} & 0 \\ 0 & 0 & 0 & 1 \end{array}\right]\left[\begin{array}{cccc} 1 & 0 & 0 & -\frac{r+l}{2} \\ 0 & 1 & 0 & -\frac{t+b}{2} \\ 0 & 0 & 1 & -\frac{n+f}{2} \\ 0 & 0 & 0 & 1 \end{array}\right]=\left[\begin{array}{cccc} \frac{2}{r-l} & 0 & 0 & -\frac{r+l}{r-l} \\ 0 & \frac{2}{t-b} & 0 & -\frac{t+b}{t-b} \\ 0 & 0 & \frac{2}{n-f} & -\frac{n+f}{n-f} \\ 0 & 0 & 0 & 1 \end{array}\right] Mortho = r−l20000t−b20000n−f200001 100001000010−2r+l−2t+b−2n+f1 = r−l20000t−b20000n−f20−r−lr+l−t−bt+b−n−fn+f1
3.透视投影
透视投影可以看作是将视锥体的大端进行压缩成长方体视窗体。透视投影矩阵可以写成如下形式:
M persp = M ortho M persp → ortho M_{\text {persp }}=M_{\text {ortho }} M_{\text {persp } \rightarrow \text { ortho }} Mpersp =Mortho Mpersp → ortho
压缩过程需要满足以下两个条件:
1.所有近平面的坐标不发生改变
2.远平面的z坐标不发生改变。
教程中根据上述条件可以推出
M persp → ortho = ( n 0 0 0 0 n 0 0 0 0 n + f − n f 0 0 1 0 ) M_{\text {persp } \rightarrow \text { ortho }}=\left(\begin{array}{cccc} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n+f & -nf \\ 0 & 0 & 1 & 0 \end{array}\right) Mpersp → ortho = n0000n0000n+f100−nf0
所以投影矩阵如下:
M persp = M ortho M persp → ortho = [ 2 r − l 0 0 − r + l r − l 0 2 t − b 0 − t + b t − b 0 0 2 n − f − n + f n − f 0 0 0 1 ] [ n 0 0 0 0 n 0 0 0 0 n + f − n f 0 0 1 0 ] = [ 2 n r − l 0 r + l l − r 0 0 2 n t − b t + b b − t 0 0 0 n + f n − f − 2 n f n − f 0 0 1 0 ] M_{\text {persp }}=M_{\text {ortho }} M_{\text {persp } \rightarrow \text { ortho }}= \left[\begin{array}{cccc} \frac{2}{r-l} & 0 & 0 & -\frac{r+l}{r-l} \\ 0 & \frac{2}{t-b} & 0 & -\frac{t+b}{t-b} \\ 0 & 0 & \frac{2}{n-f} & -\frac{n+f}{n-f} \\ 0 & 0 & 0 & 1 \end{array}\right] \left[\begin{array}{cccc} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n+f & -nf \\ 0 & 0 & 1 & 0 \end{array}\right]= \left[\begin{array}{cccc} \frac{2n}{r-l} & 0 & \frac{r+l}{l-r} & 0 \\ 0 & \frac{2n}{t-b} & \frac{t+b}{b-t} & 0 \\ 0 & 0 & \frac{n+f}{n-f} & -\frac{2nf}{n-f} \\ 0 & 0 & 1 & 0 \end{array}\right] Mpersp =Mortho Mpersp → ortho = r−l20000t−b20000n−f20−r−lr+l−t−bt+b−n−fn+f1 n0000n0000n+f100−nf0 = r−l2n0000t−b2n00l−rr+lb−tt+bn−fn+f100−n−f2nf0
此时投影矩阵就算推导完毕,但是投影接口的参数是:张角 f o v fov fov,纵横比 a s p e c t aspect aspect,近平面到原点的距离 n e a r near near,远平面到原点的距离 f a r far far
下面将矩阵中的参数都转为接口中的入参:
一般情况下,长方体视窗体是轴对称,故有 l = − r , b = − t l=-r,b=-t l=−r,b=−t,由于从原点看向 − z -z −z方向看去,所以 n = − n e a r , f = − f a r n=-near,f=-far n=−near,f=−far
w = r − l , h = t − b , t a n ( f o v 2 ) = h / 2 n e a r , a s p e c t = w h , w=r-l,\\ h=t-b,\\ tan(\frac{fov}{2})=\frac{h/2}{near},aspect=\frac{w}{h}, w=r−l,h=t−b,tan(2fov)=nearh/2,aspect=hw,
故
h = 2 ∗ n e a r ∗ t a n ( f o v 2 ) w = h ∗ a s p e c t = 2 ∗ n e a r ∗ t a n ( f o v 2 ) ∗ a s p e c t h=2*near *tan(\frac{fov}{2})\\ w=h*aspect=2*near *tan(\frac{fov}{2})*aspect h=2∗near∗tan(2fov)w=h∗aspect=2∗near∗tan(2fov)∗aspect
化简后
M persp = [ − 1 a s p e c t ∗ t a n ( f o v 2 ) 0 0 0 0 − 1 t a n ( f o v 2 ) 0 0 0 0 n e a r + f a r n e a r − f a r 2 ∗ n e a r ∗ f a r n e a r − f a r 0 0 1 0 ] M_{\text {persp }}=\left[\begin{array}{cccc} -\frac{1}{aspect*tan(\frac{fov}{2})} & 0 & 0 & 0 \\ 0 & -\frac{1}{tan(\frac{fov}{2})} & 0 & 0 \\ 0 & 0 & \frac{near+far}{near-far} & \frac{2*near*far}{near-far} \\ 0 & 0 & 1 & 0 \end{array}\right] Mpersp = −aspect∗tan(2fov)10000−tan(2fov)10000near−farnear+far100near−far2∗near∗far0
这个结果和glm库中实现不同
template<typename T>GLM_FUNC_QUALIFIER mat<4, 4, T, defaultp> perspectiveRH_NO(T fovy, T aspect, T zNear, T zFar){assert(abs(aspect - std::numeric_limits<T>::epsilon()) > static_cast<T>(0));T const tanHalfFovy = tan(fovy / static_cast<T>(2));mat<4, 4, T, defaultp> Result(static_cast<T>(0));Result[0][0] = static_cast<T>(1) / (aspect * tanHalfFovy);Result[1][1] = static_cast<T>(1) / (tanHalfFovy);Result[2][2] = - (zFar + zNear) / (zFar - zNear);Result[2][3] = - static_cast<T>(1);Result[3][2] = - (static_cast<T>(2) * zFar * zNear) / (zFar - zNear);return Result;}
都是右手坐标系,为什么不同呢?博客对此进行了解释。主要由于glm 是基于 n , f n,f n,f都是正值进行推导的,同时,glm的透视投影中还进行了NDC坐标转换,而NDC坐标系是左手坐标系。
完整代码如下:
constexpr double MY_PI = 3.1415926;inline double DEG2RAD(double deg) { return deg * MY_PI / 180; }
Eigen::Matrix4f get_model_matrix(float rotation_angle)
{Eigen::Matrix4f model = Eigen::Matrix4f::Identity();double rad = DEG2RAD(rotation_angle);model << cos(rad), -sin(rad), 0, 0,sin(rad), cos(rad), 0, 0,0, 0, 1, 0,0, 0, 0, 1;return model;
}Eigen::Matrix4f get_projection_matrix(float eye_fov, float aspect_ratio,float zNear, float zFar)
{Eigen::Matrix4f projection = Eigen::Matrix4f::Identity();double rad = DEG2RAD(eye_fov/2);projection << -1/(aspect_ratio * tan(rad)),0, 0, 0,0, -1/tan(rad), 0, 0,0, 0, (zNear+zFar) /(zNear - zFar), 2*zNear*zFar/(zNear - zFar),0, 0, 1, 0;return projection;
}
参考文献
OpenGL NDC 左手还是右手?
Games101中的透视矩阵和glm::perspective的关系
相关文章:

games101作业1
题目 给定三维下三个点 v0(2.0, 0.0, −2.0), v1(0.0, 2.0, −2.0), v2(−2.0, 0.0, −2.0), 你需要将这三个点的坐标变换为屏幕坐标并在屏幕上绘制出对应的线框三角形 (在代码框架中,我们已经提供了 draw_triangle 函数,所以你只需要去构建变换矩阵即可…...

LeetCode 面试题 02.08. 环路检测
文章目录 一、题目二、C# 题解 一、题目 给定一个链表,如果它是有环链表,实现一个算法返回环路的开头节点。若环不存在,请返回 null。 如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了…...
【Linux】线程安全-生产者消费者模型
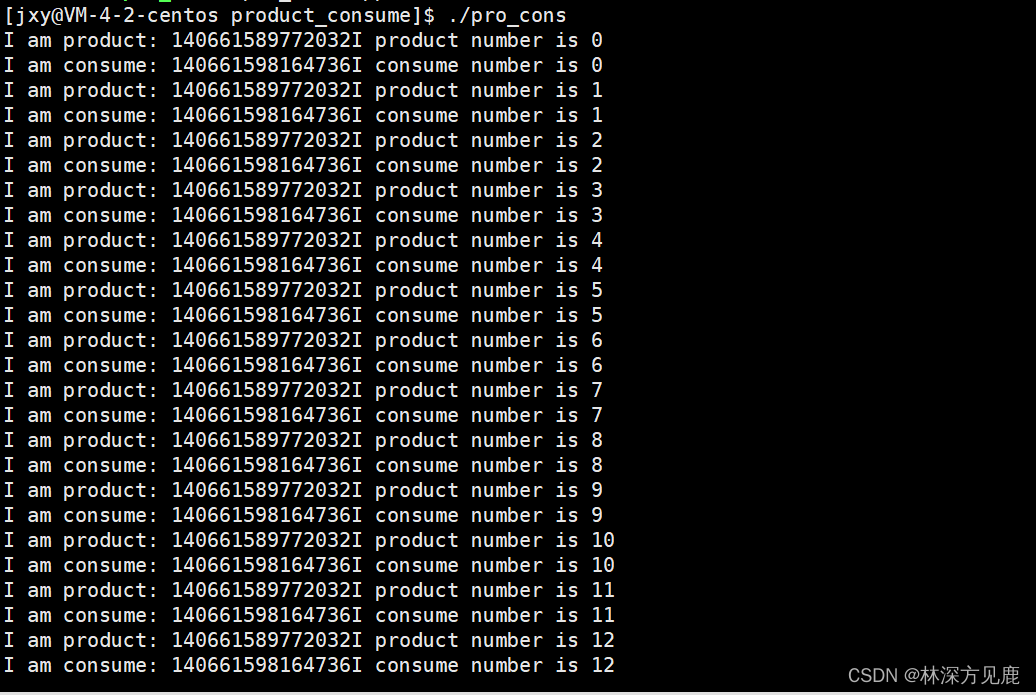
文章目录 生产者消费者模型123规则应用场景优点忙闲不均生产者和消费者解耦支持高并发 代码模拟 生产者消费者模型 123规则 1个线程安全的队列:只要保证先进先出特性的数据结构都可以称为队列 这个队列要保证互斥(就是保证当前只有一个线程对队列进行操…...
 2023/09/03)
优化(2) 2023/09/03
今天重新温习了下clean abap,以前只是偶尔打开看几眼。今天把有些自己不熟悉的地方,重点研究了下。有几个点可以在以后工作使用。这几点可能并不能提升程序效率,但会大大提高代码可读性和代码的可扩展性: 用insert XXX into tabl…...

Swap and Reverse 题解
Swap and Reverse 题面翻译 题目描述 本题共有 t t t 组数据。 给定一个长度为 n n n 的字符串 s s s 和一个整数 k k k, s s s 只包含小写字母,你可以进行若干次操作(可以是零次),具体操作如下: 选…...
单元测试:优雅编写Kotlin单元测试
一、MockK简介 MockK是一款功能强大、易于使用的Kotlin mocking框架。在编写单元测试时,MockK能够帮助我们简化代码、提高测试覆盖率,并改善测试的可维护性。除了基本用法外,MockK还提供了许多额外的功能和灵活的用法,让我们能够…...
深度学习入门教学——卷积神经网络CNN
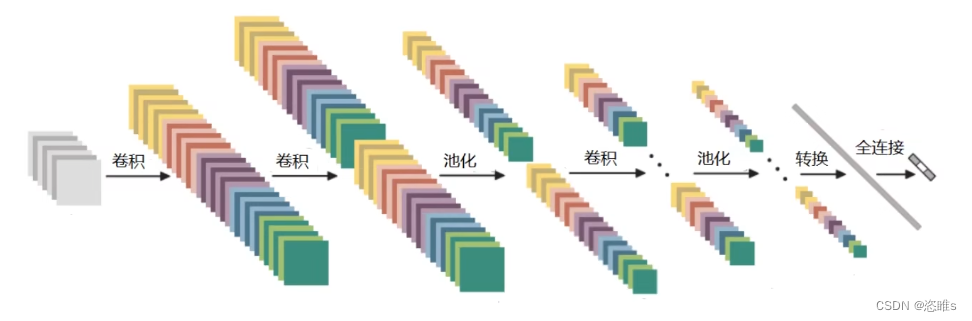
目录 一、CNN简介 一、输入层 二、卷积层 三、池化层 四、全连接层 一、CNN简介 1、应用领域 检测任务 分类与检索 超分辨率重构 2、卷积网络与传统网咯的区别 传统神经网络和卷积神经网络都是用来提取特征的。神经网络: 可以将其看作是一个二维的。卷积神经…...
列表(mysqld --verbose --help的结果例))
【MySQL】MySQL系统变量(system variables)列表(mysqld --verbose --help的结果例)
文章目录 【MySQL】MySQL系统变量(system variables)列表(mysqld --verbose --help的结果例)mysqld --verbose --help的结果例参考 【免责声明】文章仅供学习交流,观点代表个人,与任何公司无关。 编辑|SQL和…...
Python学习之四 数据输入与输出
(一) 脚本编程 前面的章节,组要学习了一些简单的Python编程,使用的是交互式解释器,本章节将开始进行脚本编程。可以使用多种编辑器或者IDE完成编码,主要使用vim。 参考前续小节的写法,我们给a、b分别赋值3和5。 在终端运行程序后发现,没有任何输出。这就是本次我们将要…...

VBA技术资料MF51:VBA_在Excel中突出显示唯一值
【分享成果,随喜正能量】世间万物,因果循环不休,你的善心善行,都可能成为你的善缘善果。每天忆佛念佛,每天都在佛菩萨的加持下生活,自然吉祥如意,法喜充满。 。 我给VBA的定义:VBA是…...
Mqtt学习笔记--交叉编译移植(1)
简述 Mqtt目前在物联网行业的应用比较多,mqtt属于应用层的一个中间件,这个中间件实现消息的订阅发布机制。网上介绍Mqtt的实现原来的比较多,这里不细介绍。 其实在我们之前的产品中,自己也开发的有类似的中间件,除了具…...
Gateway的服务网关
Gateway服务网关 Gateway网关是我们服务的守门神,所有微服务的统一入口。 网关的核心功能特性: 请求路由 权限控制 限流 架构如下: gateway使用 引入依赖 创建gateway服务,引入依赖 <!--网关--> <dependency>…...

信息化发展18
存储技术 1 、存储分类 2 、常用存储模式的技术与应用对比: ( 1 ) 存储虚拟化( Storage Virtualization ) 是“ 云存储” 的核心技术之一。 它带给人们直接的好处是提高了存储利用率, 降低了存储成本, 简…...
TypeScript学习 + 贪吃蛇项目
TypeSCript简介 TypeScript是JavaScript的超集。它对JS进行了扩展,向JS中引入了类型的概念,并添加了许多新的特性。TS代码需要通过编译器编译为JS,然后再交由JS解析器执行。TS完全兼容JS,换言之,任何的JS代码都可以直…...

YOLO-NAS详细教程-介绍如何进行物体检测
对象检测是计算机视觉中的一项核心任务,可以检测和分类图像中的边界框。自从深度学习首次取得突破以来,它就以极快的速度获得普及和普及,并推动了医疗领域、监控、智能购物等众多公司的发展。考虑到它最终满足了两个基本需求,这一点也就不足为奇了端到端方式:找到所有当前…...

容器没有命令时,如何查看进程、容器executable file not found in $PATH: unknown
前言 当容器没有ps -ef命令时,可以通过以下的命令来查看容器的进程。 docker container top查看容器运行的进程(该命令很有用) #docker container top 命令用于查看容器运行的进程 #当容器里面没有ps -ef命令时,使用docker con…...

如何使用 Amazon EMR 在 Amazon EKS 上构建可靠、高效、用户友好的 Spark 平台
这是 SafeGraph 技术主管经理 Nan Zhu 与亚马逊云科技高级解决方案架构师 Dave Thibault 共同撰写的特约文章。 SafeGraph 是一家地理空间数据公司,管理着全球超过 4100 万个兴趣点(POI,Point of Interest),提供品牌隶…...

国产IDE如何获得捐赠和风险投资
有人在开发VB6 脚本工具,有人在开发VB6的插件,把VB6变成VSCODE界面模式,再加上NUGET,NPM等包管理器原理的在线组件、源码下载功能。 还有TWINBASIC几乎80%代替了VB6,radbasic一直封闭,听说也收到了不少众筹…...

【数学建模】清风数模正课5 相关性分析
相关系数 相关性分析的关键是计算相关系数,在本节课中将会介绍两种常用的相关系数:皮尔逊相关系数(Pearson)和斯皮尔曼相关系数(Spearman)。 它们可以用来衡量两个变量间相关性的大小,对于不同…...

Java设计模式:一、六大设计原则-03:里氏替换原则
文章目录 一、定义:里氏替换原则1.1 里氏替换原则1.2 里氏替换原则的作用 二、模拟场景:里氏替换原则三、违背方案:里氏替换原则3.1 工程结构3.2 储蓄卡和信用卡3.2.1 储蓄卡3.2.2 信用卡 3.3 单元测试3.3.1 储蓄卡测试3.3.2 信用卡测试 四、…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...
