浙大陈越何钦铭数据结构07-图6 旅游规划【最小堆实现】
题目:
题目和浙大陈越何钦铭数据结构07-图6 旅游规划是一样的,不同的是用最小堆实现函数【FindMinDist】。
时间复杂度对比:
浙大陈越何钦铭数据结构07-图6 旅游规划:
创建图(CreateGraph):时间复杂度为O(N^2),因为需要使用两层循环初始化邻接矩阵。
插入边(InsertEdge):时间复杂度为O(1),因为只是将边的距离和代价插入到邻接矩阵中。
构建图(BuildGraph):时间复杂度为O(E),其中E为边的个数。需要进行E次的边的插入操作。
查找未被收录顶点中dist最小者(FindMinDist):时间复杂度为O(N),需要遍历所有未收录的顶点,查找其中dist最小的顶点。
Dijkstra算法主循环:时间复杂度为O(N^2),每次循环都需要找到未收录顶点中dist最小的顶点,并更新其周围顶点的dist和cost值。
综上所述,整个算法的时间复杂度为O(N^2)。
堆实现代码:
如果将 FindMinDist 函数使用最小堆实现,会使得 Dijkstra 算法的时间复杂度变为 O((N + E)logN),其中 N 为顶点数,E 为边数。
具体分析如下:
创建图(CreateGraph):时间复杂度仍为 O(N^2),与之前相同。
插入边(InsertEdge):时间复杂度仍为 O(1),与之前相同。
构建图(BuildGraph):时间复杂度仍为 O(E),与之前相同。
查找未被收录顶点中dist最小者(FindMinDist):使用最小堆实现后,每次查找最小值的时间复杂度为 O(logN),总共需要进行 N 次查找,因此时间复杂度为 O(NlogN)。
Dijkstra算法主循环:在每个节点更新最短路径时,需要将其邻接节点的信息插入最小堆中,插入一个节点的时间复杂度为 O(logN),总共需要插入 E 个节点,因此时间复杂度为 O(ElogN)。同时,在每个节点更新最短路径时,还需要进行一次堆操作,将堆中的最小值取出,时间复杂度为 O(logN),总共需要进行 N 次堆操作,因此时间复杂度为 O(NlogN)。
综上所述,使用最小堆实现的 Dijkstra 算法的时间复杂度为 O((N + E)logN)。相比于之前的 O(N^2),当图的规模较大时,使用最小堆可以提高算法的效率。
代码:
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>#define MAX_VERTEX_NUM 500
#define MAX_DIST 501
#define MAX_COST 501
#define ERROR -1
#define MIN_DATA -1000typedef int ELEMENT_TYPE;
typedef int Vertex;struct _MinHeap
{ELEMENT_TYPE *Elements;int Size;int Capacity;
};
typedef struct _MinHeap *MinHeap;struct _Edge
{Vertex V, W;int dist, cost;
};
typedef struct _Edge *Edge;struct _MGraph
{int Nv, Ne;int dist[MAX_VERTEX_NUM][MAX_VERTEX_NUM];int cost[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
};
typedef struct _MGraph *MGraph; /* 以邻接矩阵存储的图的类型 */void InsertEdge(MGraph G, Edge E); // 插入边
MGraph CreateGraph(int vertexNum); // 初始化图
MGraph BuildGraph();bool isEmpty(MinHeap H);
bool isFull(MinHeap H);
void PercUp(MinHeap H, int p, int dist[]);
ELEMENT_TYPE DelMin(MinHeap H, int dist[]);
void FreeHeap(MinHeap H);
MinHeap CreateHeap(int MaxSize);
void BuildMinHeap(MinHeap H, int dist[]);Vertex FindMinDist(MinHeap H, int dist[]);
void Dijkstra(MGraph G, int dist[], int cost[], Vertex S);Vertex src, dst;
// 对于全局的int数组自动初始化为0,bool数组初始化为false
int dist[MAX_VERTEX_NUM];
int cost[MAX_VERTEX_NUM];
bool collected[MAX_VERTEX_NUM];/*
07-图6 旅游规划
难度:3颗星4 5 0 3
0 1 1 20
1 3 2 30
0 3 4 10
0 2 2 20
2 3 1 203 40*/int main()
{MGraph G = BuildGraph();Dijkstra(G, dist, cost, src);printf("%d %d\n", dist[dst], cost[dst]);return 0;
}MGraph CreateGraph(int vertexNum)
{MGraph G = (MGraph)malloc(sizeof(struct _MGraph));G->Nv = vertexNum;G->Ne = 0;Vertex V, W;for (V = 0; V < vertexNum; V++){for (W = 0; W < vertexNum; W++){G->dist[V][W] = MAX_DIST;G->cost[V][W] = MAX_COST;}}return G;
}void InsertEdge(MGraph G, Edge E)
{/* 插入边<V,W> */G->dist[E->V][E->W] = E->dist;G->cost[E->V][E->W] = E->cost;/* 若是无向图则要反向也插入 */G->dist[E->W][E->V] = E->dist;G->cost[E->W][E->V] = E->cost;
}MGraph BuildGraph()
{MGraph G;Edge E;int Nv, Ne;scanf("%d %d %d %d", &Nv, &Ne, &src, &dst);G = CreateGraph(Nv);if (Ne){G->Ne = Ne;E = (Edge)malloc(sizeof(struct _Edge));for (int i = 0; i < G->Ne; i++){scanf("%d %d %d %d", &E->V, &E->W, &E->dist, &E->cost);InsertEdge(G, E);}free(E);}return G;
}Vertex FindMinDist(MinHeap H, int dist[])
{Vertex minV = ERROR;// 从堆中取出最小值,并维护最小堆的有效性。minV = DelMin(H, dist);return minV;
}void Dijkstra(MGraph G, int dist[], int cost[], Vertex S)
{Vertex V, W;/* 初始化:此处默认邻接矩阵中不存在的边用INFINITY表示 */for (V = 0; V < G->Nv; V++){ // dist和cost分别保存的是源点到顶点V的距离和开销dist[V] = G->dist[S][V];cost[V] = G->cost[S][V];}/* 先将起点收入集合 */dist[S] = 0;cost[S] = 0;collected[S] = true;// 根据dist对未收录顶点创建最小堆MinHeap H = CreateHeap(MAX_VERTEX_NUM);for (V = 0; V < G->Nv; V++){if (collected[V] == false){ // H->Elements保存的是未收集顶点的编号,本例依次是1,2,3H->Elements[++H->Size] = V;}}BuildMinHeap(H, dist);while (1){/* V = 未被收录顶点中dist最小者 */V = FindMinDist(H, dist);if (V == ERROR) /* 若这样的V不存在 */break; /* 算法结束 */collected[V] = true; /* 收录V */for (W = 0; W < G->Nv; W++) /* 对图中的每个顶点W *//* 若W是V的邻接点并且未被收录 */if (collected[W] == false && G->dist[V][W] < MAX_DIST){if (G->dist[V][W] < 0) /* 若有负边 */return; /* 不能正确解决,返回错误标记 *//* 若收录V使得dist[W]变小 */if (dist[V] + G->dist[V][W] < dist[W]){dist[W] = dist[V] + G->dist[V][W]; /* 更新dist[W] */cost[W] = cost[V] + G->cost[V][W];}else if (dist[V] + G->dist[V][W] == dist[W] &&cost[V] + G->cost[V][W] < cost[W]){cost[W] = cost[V] + G->cost[V][W];}}} /* while结束*/FreeHeap(H);free(G);
}bool isEmpty(MinHeap H)
{return H->Size == 0;
}bool isFull(MinHeap H)
{return H->Size == H->Capacity;
}ELEMENT_TYPE DelMin(MinHeap H, int dist[])
{if (!isEmpty(H)){ELEMENT_TYPE min, last;int parent, child;min = H->Elements[1];last = H->Elements[H->Size--];for (parent = 1; 2 * parent <= H->Size; parent = child){child = 2 * parent;if ((child != H->Size) && (dist[H->Elements[child]] > dist[H->Elements[child + 1]])){child++;}if (dist[last] <= dist[H->Elements[child]]){break;}else{H->Elements[parent] = H->Elements[child];}}H->Elements[parent] = last;return min;}else{return ERROR;}
}void PercUp(MinHeap H, int p, int dist[])
{ /*根据顶点的dist值,决定顶点在堆中的存储位置。对dist[H->Elements[child]] > dist[H->Elements[child + 1]]的理解dist[x] > dist[y],本质是比较两个顶点之间的dist值,x,y是顶点序号。dist[x]的初始值通过dist[V] = G->dist[S][V]获得,并用dist[W] = dist[V] + G->dist[V][W]更新child是顶点在堆中的索引,H->Elements[child]存储的是顶点序号所以dist[H->Elements[child]]是顶点的dist值。*/int parent, child;ELEMENT_TYPE X;X = H->Elements[p];for (parent = p; 2 * parent <= H->Size; parent = child){child = 2 * parent;if ((child != H->Size) && (dist[H->Elements[child]] > dist[H->Elements[child + 1]])){child++;}if (dist[X] <= dist[H->Elements[child]]){break;}else{H->Elements[parent] = H->Elements[child];}}H->Elements[parent] = X;
}void FreeHeap(MinHeap H)
{if (H != NULL){free(H->Elements);free(H);}
}MinHeap CreateHeap(int MaxSize)
{MinHeap H = (MinHeap)malloc(sizeof(struct _MinHeap));H->Elements = (ELEMENT_TYPE *)malloc((MaxSize + 1) * sizeof(ELEMENT_TYPE));H->Elements[0] = MIN_DATA;H->Size = 0;H->Capacity = MaxSize;return H;
}void BuildMinHeap(MinHeap H, int dist[])
{ // p表示顶点在堆中的位置int p;for (p = H->Size / 2; p > 0; p--){PercUp(H, p, dist);}
}
小结:
本题的最小堆比用循环的方式实现FindMinDist要难一些,主要是要理解和修改堆的几个实现,核心是构造和维护最小堆要根据dist的值,来维护对应的顶点。
相关文章:

浙大陈越何钦铭数据结构07-图6 旅游规划【最小堆实现】
题目: 题目和浙大陈越何钦铭数据结构07-图6 旅游规划是一样的,不同的是用最小堆实现函数【FindMinDist】。 时间复杂度对比: 浙大陈越何钦铭数据结构07-图6 旅游规划: 创建图(CreateGraph):时…...
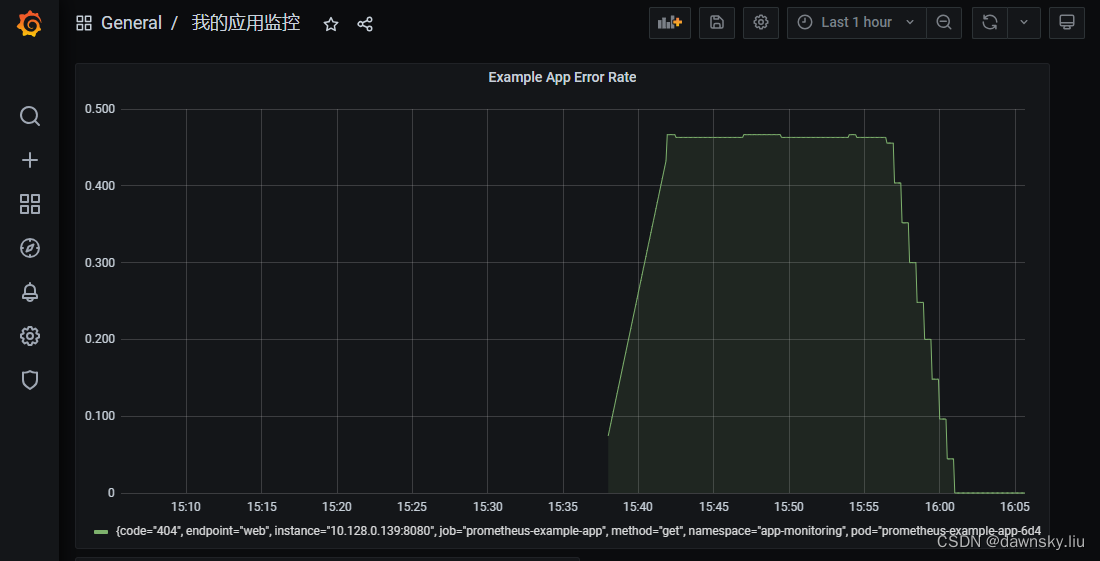
OpenShift 4 - 用 Prometheus 和 Grafana 监视用户应用定制的观测指标(视频)
《OpenShift / RHEL / DevSecOps 汇总目录》 说明:本文已经在 OpenShift 4.13 的环境中验证 文章目录 OpenShift 的监控功能构成部署被监控应用用 OpenShift 内置功能监控应用用 Grafana 监控应用安装 Grafana 运行环境配置 Grafana 数据源定制监控 Dashboard 演示视…...
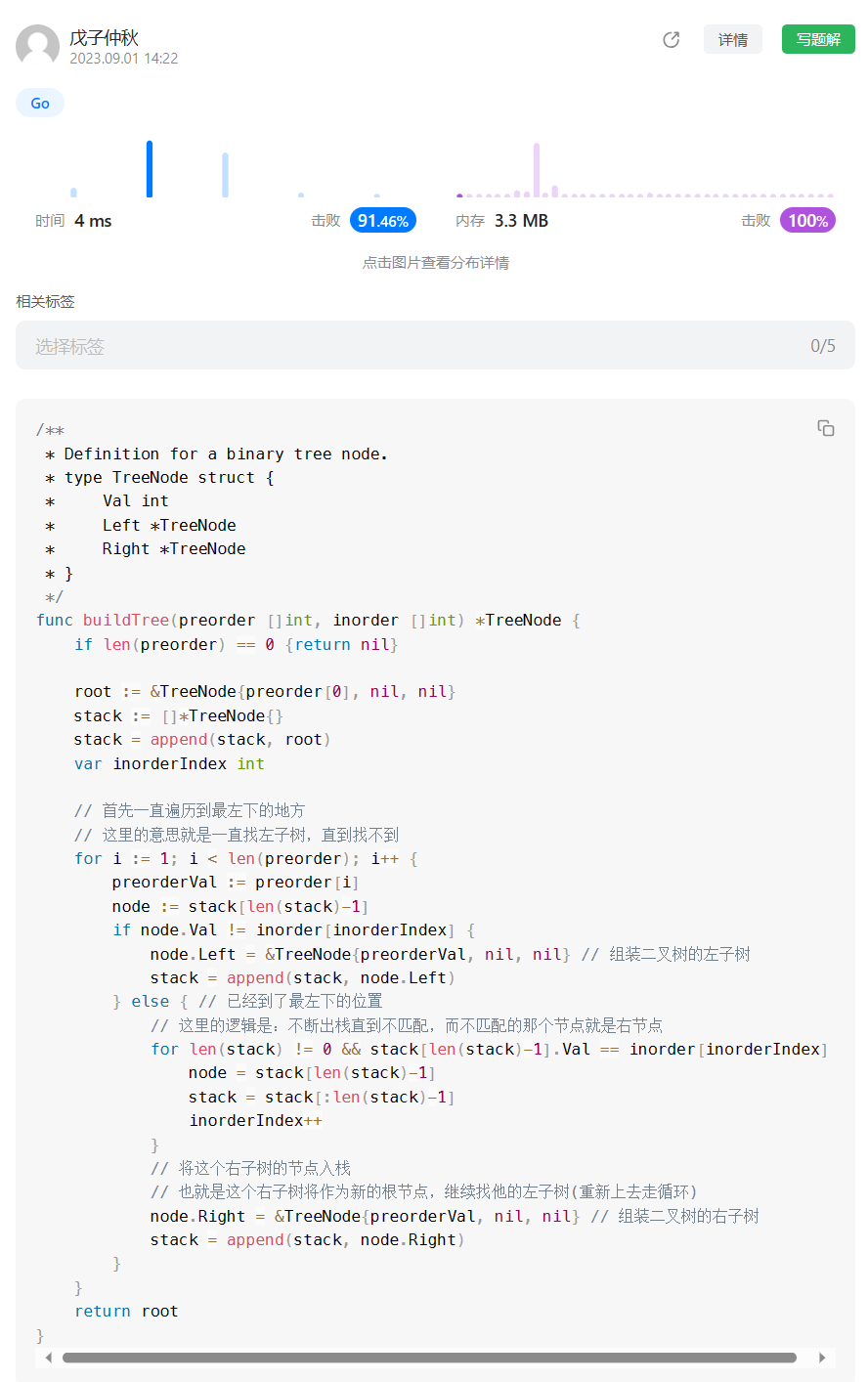
【LeetCode】剑指 Offer <二刷>(3)
目录 题目:剑指 Offer 06. 从尾到头打印链表 - 力扣(LeetCode) 题目的接口: 解题思路: 代码: 过啦!!! 题目:剑指 Offer 07. 重建二叉树 - 力扣…...

Ceph IO流程及数据分布
1. Ceph IO流程及数据分布 1.1 正常IO流程图 步骤: client 创建cluster handler。client 读取配置文件。client 连接上monitor,获取集群map信息。client 读写io 根据crshmap 算法请求对应的主osd数据节点。主osd数据节点同时写入另外两个副本节点数据。…...

Netty-NIO
文章目录 一、NIO-Selector1.处理accept2.cancel3.处理read4.处理客户端断开5. 处理消息的边界6. 写入内容过多的问题7. 处理可写事件 一、NIO-Selector 1.处理accept //1.创建selector,管理多个channel Selector selector Selector.open(); ByteBuffer buffer ByteBuffer.…...

红外物理学习笔记 ——第三章
第三章 基尔霍夫定律:就是说物体热平衡条件下,发射的辐射功率要等于吸收的辐射功率 M α E M\alpha E MαE α \alpha α 是吸收率, M M M 是幅出度(发射出去的), E E E是辐照度(外面照过来的…...

使用 htmx 构建交互式 Web 应用
学习目标:了解htmx的基本概念、特点和用法,并能够运用htmx来创建交互式的Web应用程序。 学习内容: 1. 什么是htmx? - htmx是一种用于构建交互式Web应用程序的JavaScript库。 - 它通过将HTML扩展为一种声明性的交互式语言&a…...
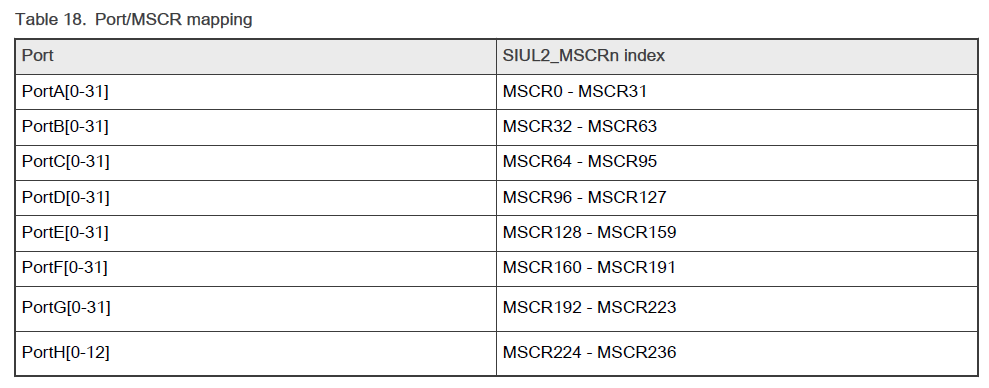
S32K324芯片学习笔记
文章目录 Core and architectureDMASystem and power managementMemory and memory interfacesClocksSecurity and integrity安全与完整性Safety ISO26262Analog、Timers功能框图内存mapflash Signal MultiplexingPort和MSCR寄存器的mapping Core and architecture 两个Arm Co…...

htmx-使HTML更强大
本文作者是360奇舞团开发工程师 htmx 让我们先来看一段俳句: javascript fatigue: longing for a hypertext already in hand 这个俳句很有意思,是开源项目htmx文档中写的,意思是说,我们已经有了超文本,为什么还要去使用javascr…...
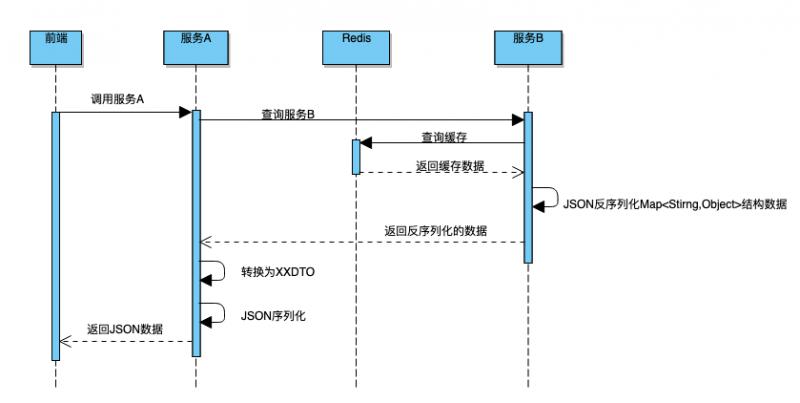
Java学习之序列化
1、引言 《手册》第 9 页 “OOP 规约” 部分有一段关于序列化的约定 1: 【强制】当序列化类新增属性时,请不要修改 serialVersionUID 字段,以避免反序列失败;如果完全不兼容升级,避免反序列化混乱,那么请…...
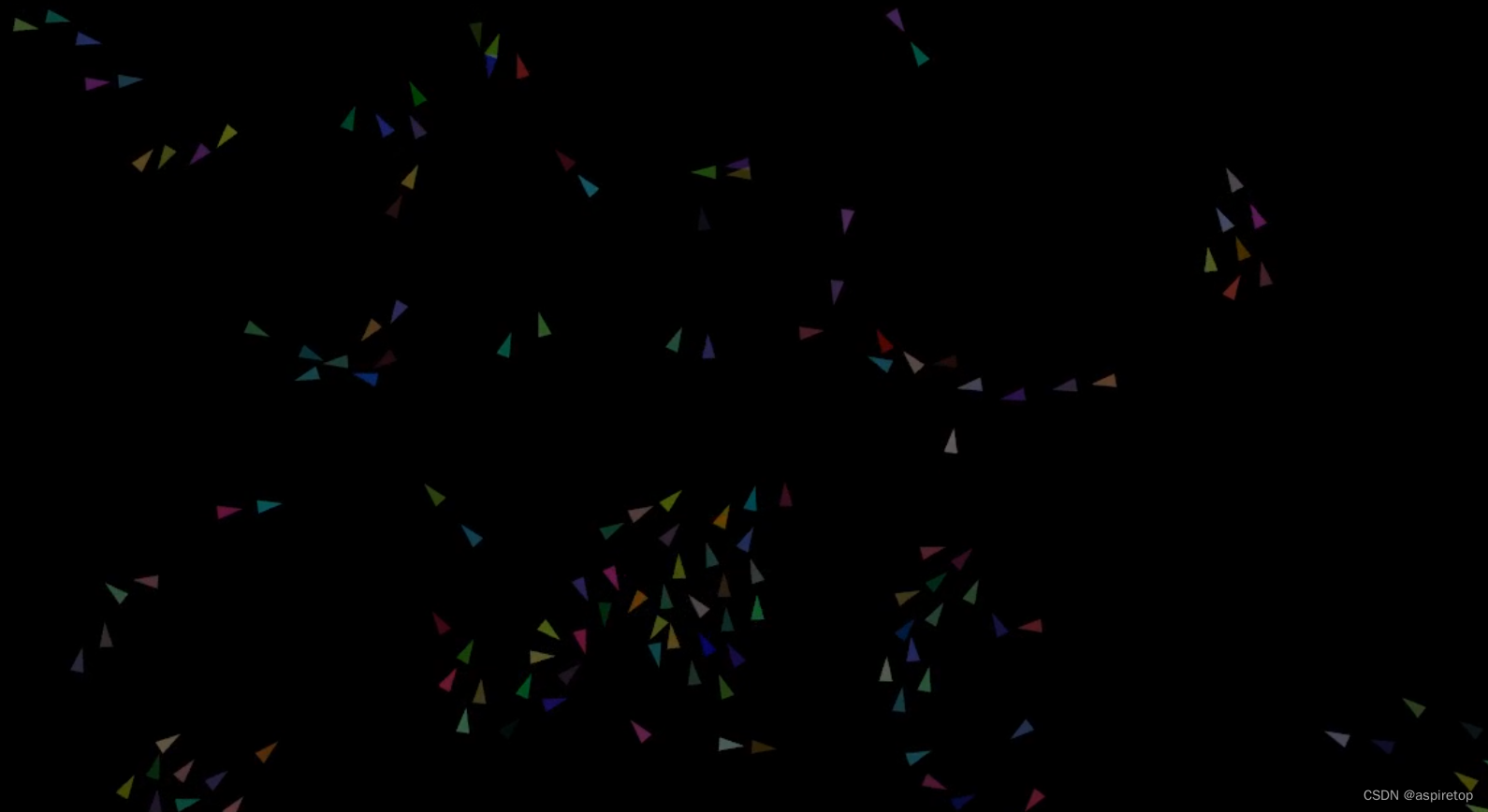
C++实现蜂群涌现效果(flocking)
Flocking算法0704_元宇宙中的程序员的博客-CSDN博客 每个个体的位置,通过计算与周围个体的速度、角度、位置,去更新位置。...
IDEA复制一个工程为多个并启动,测试负载均衡
1 找到服务按钮 2 选择复制配置 3 更改新的名称与虚拟机参数 复制下面的代码在VM参数中 -Dserver.port8082 4 最后启动即可...

001_C++语法基础
C语法基础 所有C语法要用英文区分大小写每个语句写完以分号结束 C标准输入输出头文件iostream 若想通过C实现数据的输入和输出,需要导入标准输入输出头文件 #include <iostream>标准输入输出头文件<iostream>中包含了cin输入语句和cout输出语句 标…...
对Excel表中归类的文件夹进行自动分类
首先把excel表另存为.txt文件(注意:刚开始可能是ANSI格式,需要转成UTF-8格式);再新建一个.txt文件,重命名成.bat文件(注意:直接创建的如果是是UTF-8格式,最好转成ANSI格式࿰…...
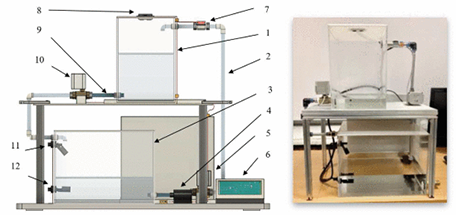
LabVIEW液压支架控制系统的使用与各种配置的预测模型的比较分析
LabVIEW液压支架控制系统的使用与各种配置的预测模型的比较分析 模型预测控制在工业中应用广泛。这种方法的优点之一是在求解最优控制问题时能够明确考虑对输入和输出状态施加的约束。控制对象模型用于有限时间范围内最优控制的实时计算。所使用的数学设备允许从具有单输入和单…...

C++中位运算符使用
& 与 只有都为1结果为1 0 & 0 00 & 1 01 & 0 01 & 1 1 | 或 只要一个为1结果为1 0|00 0|11 1|01 1|11 ^ 异或 两个相同的数字为0,其余为1 0^00 1^01 0^11 1^10 ~ 取反 将进制位数进行取反 ~1-2 //0000 0001-->代…...

微机原理 || 第2次测试:汇编指令(加减乘除运算,XOR,PUSH,POP,寻址方式,物理地址公式,状态标志位)(测试题+手写解析)
(一)测试题目: 1.数[X]补1111,1110B,则其真值为 2.在I/O指令中,可用于表示端口地址的寄存器 3. MOV AX,[BXSl]的指令中,源操作数的物理地址应该如何计算 4.执行以下两条指令后,标志寄存器FLAGS的六个状态…...

人员闯入检测告警算法
人员闯入检测告警算法通过yolov5网络模型识别检测算法,人员闯入检测告警算法对未经许可或非法进入的人员进行及时识别告警,确保对危险区域的安全管理和保护。YOLO系列算法是一类典型的one-stage目标检测算法,其利用anchor box将分类与目标定位…...
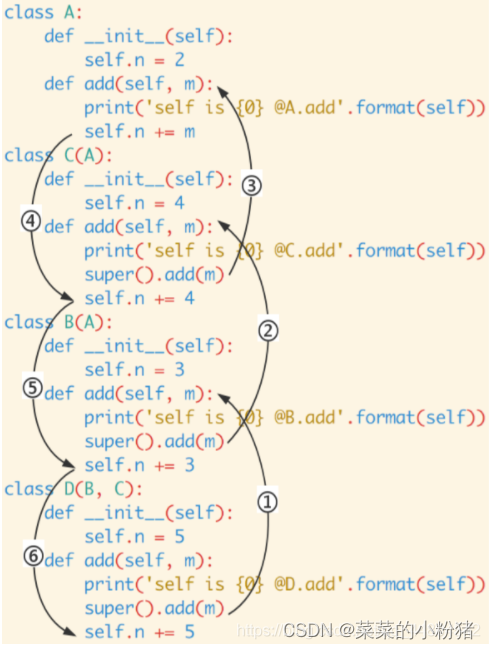
python中super()用法
super关键字的用法 一、概述二、作用三、语法四、使用示例1.通过super() 来调用父类的__init__ 构造方法:2.通过supper() 来调用与子类同名的父类方法2.1 单继承2.2 多继承 一、概述 super() 是python 中调用父类(超类)的一种方法࿰…...
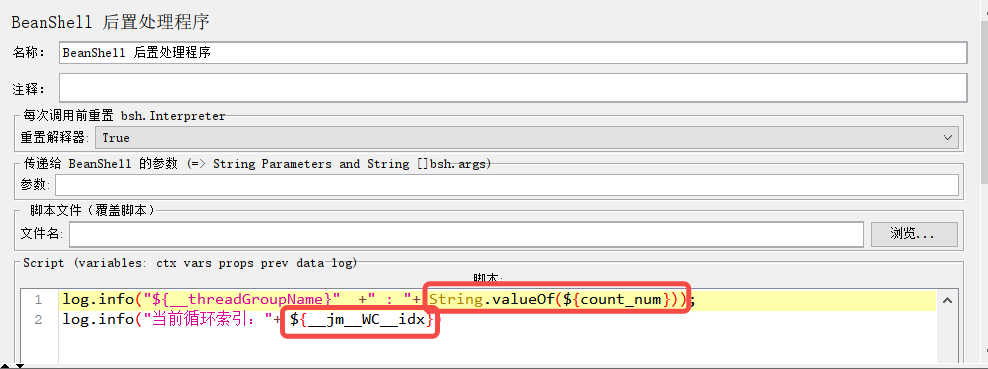
jmeter While控制器
一种常见的循环控制语句,用于重复执行一段代码块,直到指定的条件不再满足。 参数: 空LASTJMeter变量、函数、属性或任意其他可用表达式 (jmeter提供的方法)。判断变量值count_num小于等于20,推荐简单的几…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...

【大模型】RankRAG:基于大模型的上下文排序与检索增强生成的统一框架
文章目录 A 论文出处B 背景B.1 背景介绍B.2 问题提出B.3 创新点 C 模型结构C.1 指令微调阶段C.2 排名与生成的总和指令微调阶段C.3 RankRAG推理:检索-重排-生成 D 实验设计E 个人总结 A 论文出处 论文题目:RankRAG:Unifying Context Ranking…...

python基础语法Ⅰ
python基础语法Ⅰ 常量和表达式变量是什么变量的语法1.定义变量使用变量 变量的类型1.整数2.浮点数(小数)3.字符串4.布尔5.其他 动态类型特征注释注释是什么注释的语法1.行注释2.文档字符串 注释的规范 常量和表达式 我们可以把python当作一个计算器,来进行一些算术…...
