数学建模--层次分析法(AHP)的Python实现
目录
1.算法流程简介
2.算法核心代码
3.算法效果展示
1.算法流程简介
"""
AHP:层次分析法,层次分析法还是比较偏向于主观的判断的,所以在建模的时候尽可能不要去使用层次分析法
不过在某些创新的评价方法上,也是能够运用层次分析使得评价变得全面一些,有可能险中求胜,获得评委的青睐的
"""
具体流程如下:
#1.首先进行预备信息的求解便于一致性检验
#2.进行一致性检验,判断是否可以使用层次分析法
#3.求解权重的三种方法(算术平均值法,几何平均值法,特征向量法)2.算法核心代码
"""
AHP:层次分析法,层次分析法还是比较偏向于主观的判断的,所以在建模的时候尽可能不要去使用层次分析法
不过在某些创新的评价方法上,也是能够运用层次分析使得评价变得全面一些,有可能险中求胜,获得评委的青睐的
"""
import numpy as np
class AHP:
#1.首先进行预备信息的求解便于一致性检验def __init__(self,cmatrix):self.arr=cmatrix#导入比较矩阵#获取比较矩阵的相关数据self.n=cmatrix.shape[0]#比较矩阵的大小#设置RI便于一致性检验self.RI= [0, 0, 0.52, 0.89, 1.12, 1.26, 1.36, 1.41, 1.46, 1.49, 1.52, 1.54, 1.56, 1.58,1.59]#求解特征值和特征向量np.linalg.eig()会一起返回self.eig_val, self.eig_vector = np.linalg.eig(self.arr)#求解矩阵的最大特征值self.max_eig_val = np.max(self.eig_val)#矩阵最大特征值对应的特征向量self.max_eig_vector = self.eig_vector[:, np.argmax(self.eig_val)].real#矩阵的一致性指标CIself.CI_val = (self.max_eig_val - self.n) / (self.n - 1)#矩阵的一致性比例CRself.CR_val = self.CI_val / (self.RI[self.n - 1])
#2.进行一致性检验,判断是否可以使用层次分析法def consist_test(self):#一致性指标CIprint("比较矩阵的CI值为:",str(self.CI_val))#一致性指标CRprint("比较矩阵的CR值为:",str(self.CR_val))if self.n==2:print("仅有两个子因素,不存在一致性冲突问题")else:if self.CR_val<0.1:#CR<0.1,一致性问题通过print("比较矩阵CR值为:",str(self.CR_val),"<0.1,通过一致性检验!")return Trueelse:print("比较矩阵CR值为:",str(self.CR_val),">0.1,未通过一致性检验,不能使用层次分析法!")return False
#3.求解权重的三种方法:
#1.算术平均法def Arithmetic_averaging_method(self):#求每一列的和sum_col=np.sum(self.arr,axis=0)#归一化处理array_std=self.arr/sum_col#计算权重向量weight_Arithmetic_averaging=np.sum(array_std,axis=1)/self.nprint("算术平均法求得的权重为:",weight_Arithmetic_averaging)return weight_Arithmetic_averaging#2.几何平均法def Geometric_averaging_method(self):# 求矩阵的每列的积col_plus = np.product(self.arr, axis=0)# 将得到的积向量的每个分量进行开n次方array_power = np.power(col_plus, 1 / self.n)# 将列向量归一化weight_Geometric_averaging = array_power / np.sum(array_power)# 打印权重向量print("几何平均法求得的权重为:", weight_Geometric_averaging)# 返回权重向量的值return weight_Geometric_averaging#3.特征值权重法def Eigenvalue_weighting_method(self):# 将矩阵最大特征值对应的特征向量进行归一化处理就得到了权重weight_Eigenvalue_weighting = self.max_eig_vector / np.sum(self.max_eig_vector)# 打印权重向量print("特征值权重法法求得的权重为:", weight_Eigenvalue_weighting)# 返回权重向量的值return weight_Eigenvalue_weightingdef test_run_demo():#comparsion_matrix可以随意修改comparsion_matrix=np.array([[1,1/4,1/9],[4,1,1/2],[9, 2, 1]])weight1 = AHP(comparsion_matrix).Arithmetic_averaging_method()weight2 = AHP(comparsion_matrix).Geometric_averaging_method()weight3 = AHP(comparsion_matrix).Eigenvalue_weighting_method()#运行区域:
test_run_demo()3.算法效果展示
算术平均法求得的权重为: [0.07243906 0.30125047 0.62631047]
几何平均法求得的权重为: [0.7374984 0.17727613 0.08522547]
特征值权重法法求得的权重为: [0.07239208 0.30116321 0.62644471]
相关文章:
的Python实现)
数学建模--层次分析法(AHP)的Python实现
目录 1.算法流程简介 2.算法核心代码 3.算法效果展示 1.算法流程简介 """ AHP:层次分析法,层次分析法还是比较偏向于主观的判断的,所以在建模的时候尽可能不要去使用层次分析法 不过在某些创新的评价方法上,也是能够运用层次分析使得评价变得全面一些,有可…...

机器学习笔记之最优化理论与方法(三)凸集的简单认识(下)
机器学习笔记之最优化理论与方法——凸集的简单认识[下] 引言回顾:基本定义——凸集关于保持集合凸性的运算仿射变换 凸集基本性质:投影定理点与凸集的分离支撑超平面定理 引言 继续凸集的简单认识(上)进行介绍,本节将介绍凸集的基本性质以及…...
Apipost:API文档、调试、Mock与测试的一体化协作平台
随着数字化转型的加速,API(应用程序接口)已经成为企业间沟通和数据交换的关键。而在API开发和管理过程中,API文档、调试、Mock和测试的协作显得尤为重要。Apipost正是这样一款一体化协作平台,旨在解决这些问题…...

Homebrew下载安装及使用教程
Homebrew是什么? 简单来说,就是用命令行的形式去管理mac系统的包或软件。 安装命令 /bin/bash -c "$(curl -fsSL https://raw.githubusercontent.com/Homebrew/install/HEAD/install.sh)"国内请使用镜像源进行下载 执行上述命令后会要求输入…...

【Codeforces】CF193D Two Segments
题目链接 CF方向 Luogu方向 题目解法 考虑在值域上的问题:有多少段区间,对应在排列上不超过 2 2 2 段 肯定需要枚举一个端点,另一个快速算出,考虑枚举值域区间右端点 r r r,计算 l l l 可以发现,新增…...

内存管理概述
前言 在学习计算机科学时,内存管理是一个非常重要的概念。简单地说,内存是计算机用来存储和访问数据的地方。而内存管理是计算机系统如何分配、使用和管理内存的过程。 为什么要学习内存管理? 1. 高效性:内存管理能够帮助计算机更…...
Spring的重试机制-SpringRetry
在我们的日常开发中,经查会遇到调用接口失败的情况,这时候就需要通过一些方法来进行重试,比如通过while循环手动重复调用或,或者通过记录错误接口url和参数到数据库,然后手动调用接口,或者通过JDK/CGLib动态…...
水稻叶病害数据集(目标检测,yolo使用)
1.数据集文件夹 train文件夹(44229张),test文件夹(4741张),valid文件夹(6000张) 2.train文件夹展示 labels展示 标签txt展示 data.yaml文件展示 对数据集感兴趣的可以关注最后一行…...
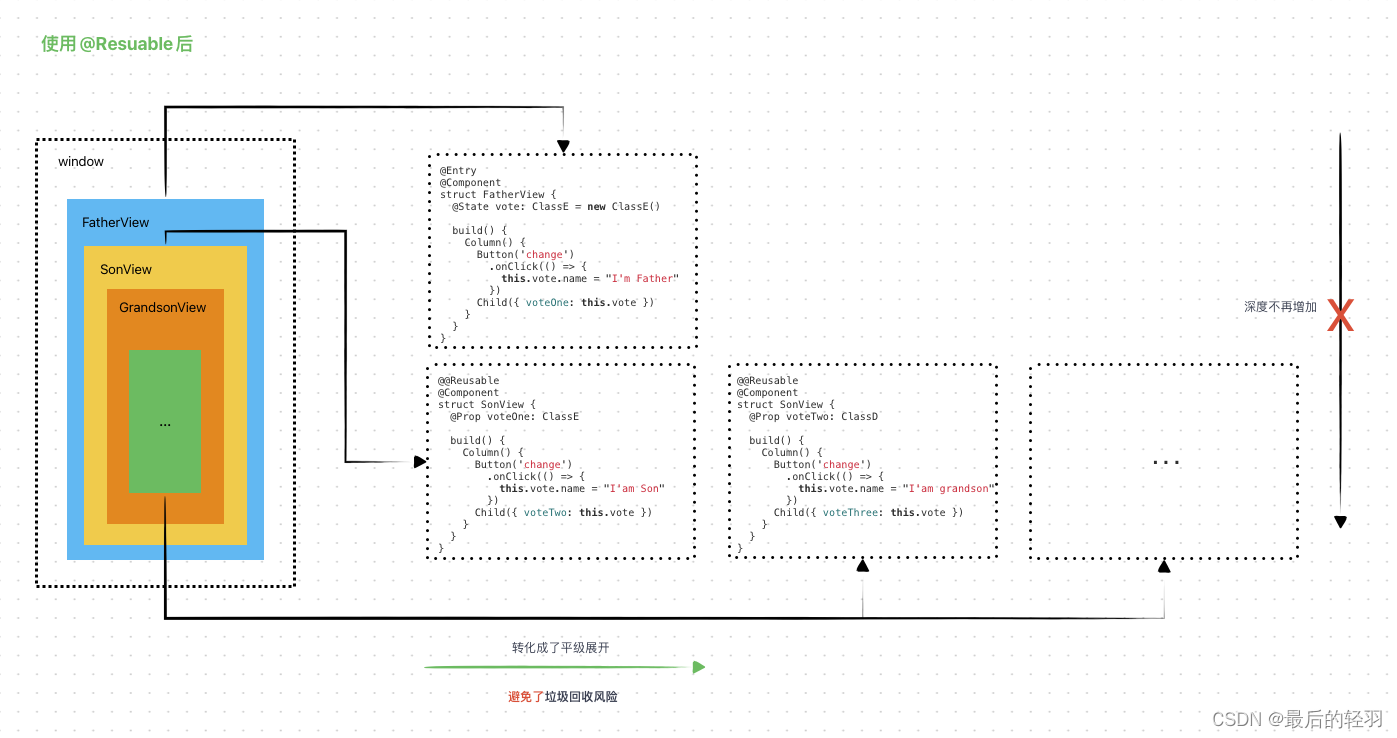
鸿蒙系列-如何使用好 ArkUI 的 @Reusable?
如何使用好 ArkUI 的 Reusable? OpenHarmony 组件复用机制 在ArkUI中,UI显示的内容均为组件,由框架直接提供的称为 系统组件,由开发者定义的称为 自定义组件。 在进行 UI 界面开发时,通常不是简单的将系统组件进行组合…...

展锐平台音频框架
Audio DT介绍 1.概述 DT(Device Tree)是一种描述硬件的数据结构,DTS即设备树源码。 2.Audio DTS 文件架构 \bsp\kernel\kernel.4.14\arch\arm64\boot\sprd ums512.dts //SOC级相关节点 ——sc2730.dtsi //Codec ——sharkl5Pro.dts…...

webpack loader和plugins的区别
在Webpack中,Loader和Plugin是两个不同的概念,用于不同的目的。 Loader是用于处理非JavaScript模块的文件的转换工具。它们将文件作为输入,并将其转换为Webpack可以处理的模块。例如,当您在Webpack配置中使用Babel Loader时&…...

适配器模式:接口的平滑过渡
欢迎来到设计模式系列的第七篇文章!在前面的几篇文章中,我们已经学习了一些常见的设计模式,今天我们将继续探讨另一个重要的设计模式——适配器模式。 适配器模式简介 适配器模式是一种结构型设计模式,它主要用于将一个类的接口…...
vscode搭建springboot开发环境
前言 idea好用到但是收money,eclipse免费但是界面有点丑,所以尝试使用vscode开发springboot 提前准备 安装jdk,jdk需要大于11 安装vscode 安装maven 安装插件 主要是下面的插件 Extension Pack for JavaSpring Boot Extension PackDepe…...
SpringMVC-学习笔记
文章目录 1.概述1.1 SpringMVC快速入门 2. 请求2.1 加载控制2.2 请求的映射路径2.3 get和post请求发送2.4 五种请求参数种类2.5 传递JSON数据2.6 日期类型参数传递 3.响应3.1 响应格式 4.REST风格4.1 介绍4.2 RESTful快速入门4.3 简化操作 1.概述 SpringMVC是一个基于Java的Web…...
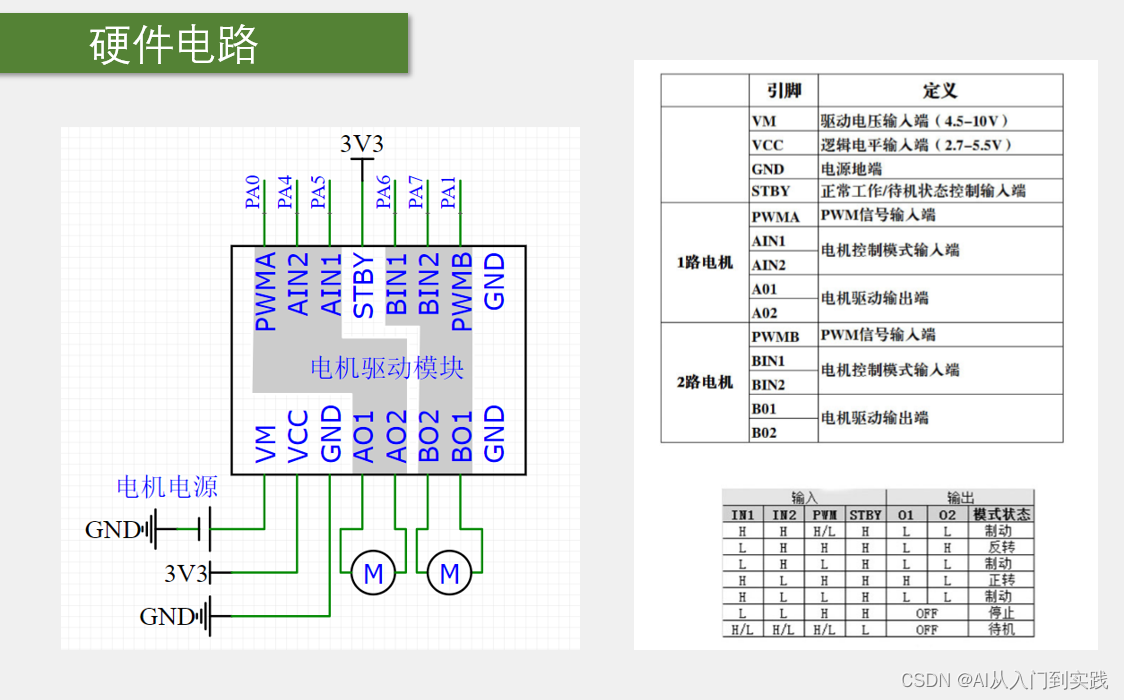
【STM32】学习笔记(TIM定时器)
TIM(Timer)定时器 定时器可以对输入的时钟进行计数,并在计数值达到设定值时触发中断 16位计数器、预分频器、自动重装寄存器的时基单元,在72MHz计数时钟下可以实现最大59.65s的定时 不仅具备基本的定时中断功能,而且…...
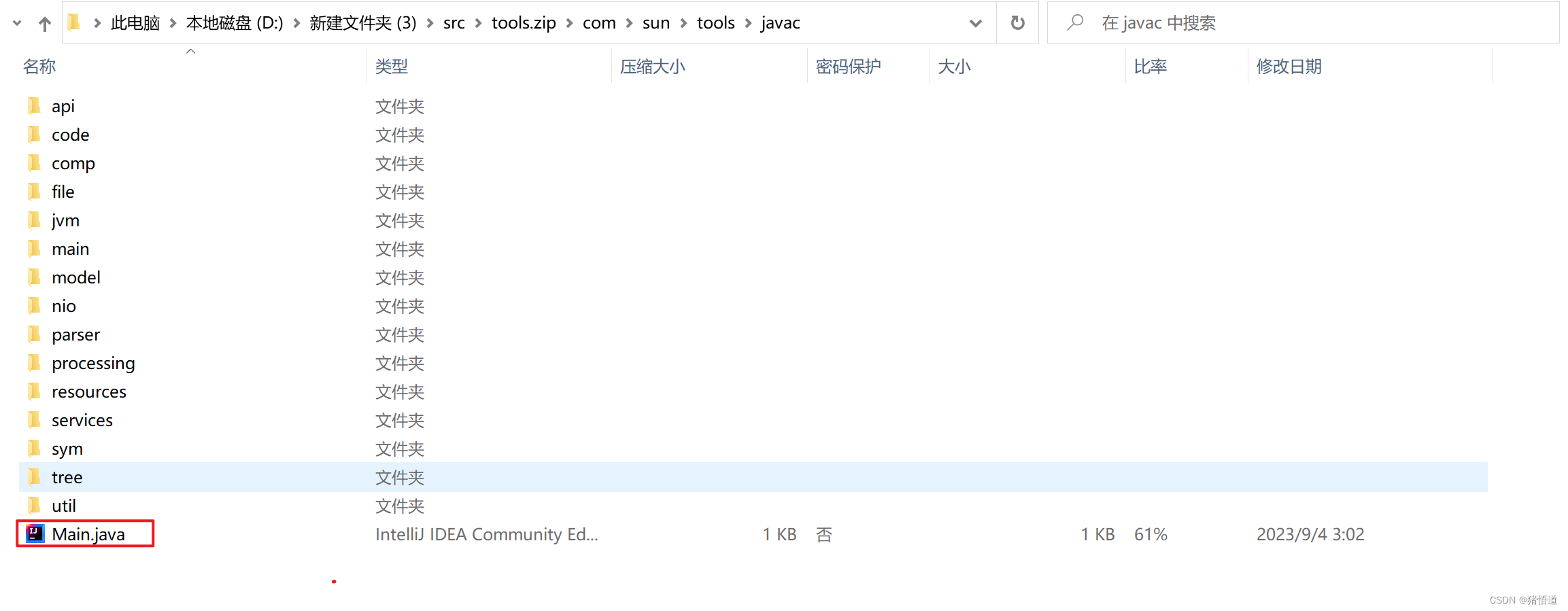
Jdk8 动态编译 Java 源码为 Class 文件(三)
Jdk8 动态编译 Java 源码为 Class 文件 一.JDK版本二.工程介绍1.依赖2.启动类3.配置类(用于测试依赖注入)4.工具类1.Java 源码文件读取类2.SpringBoot 容器实例管理类 5.测试类1.抽象类2.接口类3.默认抽象实现4.默认接口实现 6.接口类1.测试接口2.类重载…...

Shell自动化日志维护脚本
简介: 系统日志对于了解操作系统的运行状况、故障排除和性能分析至关重要。然而,长期积累的日志文件可能变得庞大,影响系统性能。在这篇文章中,我们将介绍一个自动化的解决方案,使用 Bash 脚本来监控和维护系统日志文件…...
设计模式入门笔记
1 设计模式简介 在IT这个行业,技术日新月异,可能你今年刚弄懂一个编程框架,明年它就不流行了。 然而即使在易变的IT世界也有很多几乎不变的知识,他们晦涩而重要,默默的将程序员划分为卓越与平庸两类。比如说ÿ…...

存储成本降低85%,携程历史库场景的降本实践
携程,一家中国领先的在线票务服务公司,从 1999 年创立至今,数据库系统历经三次替换。在移动互联网时代,面对云计算卷积而来的海量数据,携程通过新的数据库方案实现存储成本降低 85% 左右,性能提升数倍。本文…...

如何精确掌握函数防抖和函数节流的使用?
前序 函数防抖(Debouncing)和函数节流(Throttling)都是用于控制函数执行频率的技术,通常在处理高频率触发的事件(如窗口滚动、鼠标移动、输入框输入等)时非常有用 一、核心概念 函数防抖 函…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...
