QT实现任意阶贝塞尔曲线绘制
bezier曲线在编程中的难点在于求取曲线的系数,如果系数确定了那么就可以用微小的直线段画出曲线。bezier曲线的系数也就是bernstein系数,此系数的性质可以自行百度,我们在这里是利用bernstein系数的递推性质求取:
简单举例
两个点p0,p1 为一阶曲线,系数为 (1-u)p0+u*p1; 将系数存在数组中b[0] =1-u,b[1]=u。
三个点 p0 p1 p2 为二阶曲线,系数(1-u)(1-u)p0+2u(1-u)p1+u*u*p2 可以看出二阶的系数是一届的系数的关系 ((1-u)+u)(b[0]+b[1])。
注意:通过这个公式有没有发现,当u==0的时候这个点就是p0,当u==1的时候这个点就是p2,其他时候点被p1所吸引,也就是p1点的存在会导致(u!=0&&u!=1)的时候生成的点靠近p1。
四个点 三阶曲线为:
((1-u)+u)((1-u)+u)(b[0]+b[1])
是不是有种似曾相识的感觉,对了,这就是高中牛顿二项式展开的过程:

二阶贝塞尔曲线实现代码:
QPointF p0(0,0);
QPointF p1(1000,0);
QPointF p2(1000,1000);
QPainterPath path;
path.moveTo(p0);
QPointF pTemp;
for(double t=0; t<1; t+=0.01) //2次Bezier曲线
{pTemp =pow((1-t),2)*p0+2*t*(1-t)*p1+pow(t,2)*p2;path.lineTo(pTemp);
}没有使用贝塞尔曲线(三个点直接相连)画出来三角形是这样:

使用贝塞尔曲线之后,(1000,0)这个位置的角会圆化:
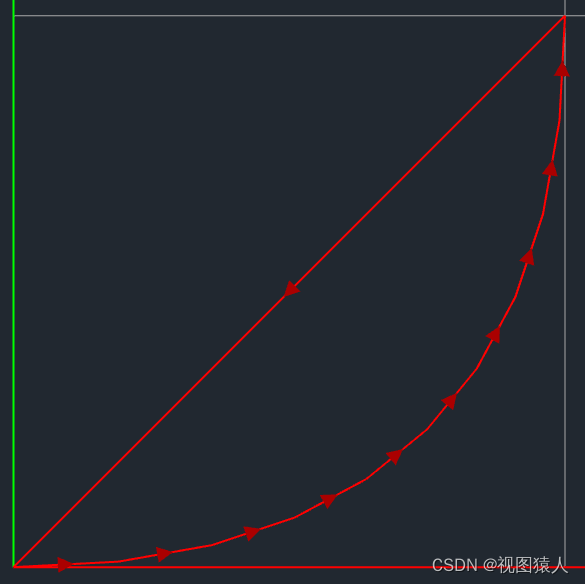
上图中你会发现曲线不太圆滑,这个你可以调参数precision,主要的问题是它用了贝塞尔曲线之后都不像一个三角形了,我们只想对三角形的角进行圆化。我们可以选择构成三角形角的两边上接近交点位置的两个点,用这个两个点和这两边的交点(三角形的角)生成贝塞尔曲线,效果如下:
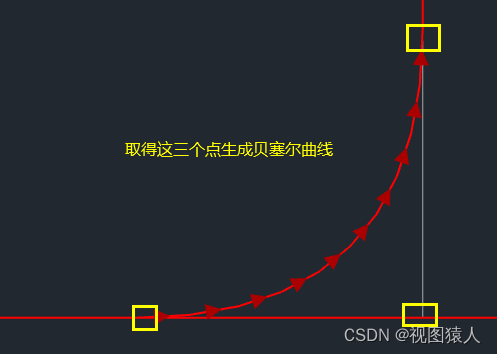
我们发现他就是有很多短小的曲线构成的,所以这就是多边形的角圆化的原理。
上面是实现的二阶贝塞尔曲线,但是有时候我们可能会使用其他阶数曲线,所以我们需要改一下代码使得代码更大众化:
/*** @brief createNBezierCurve 生成N阶贝塞尔曲线点* @param src 源贝塞尔控制点,里面有两个点就是一阶,有三个点就是二阶,依次类推* @param dest 目的贝塞尔曲线点* @param precision 生成精度,控制着细小直线的长度,细小直线长度越小模拟出现的圆角越圆滑(此值越小细小直线长度越小)*/
static void createNBezierCurve(const QList<QPointF> &src, QList<QPointF> &dest, qreal precision=0.5)
{if (src.size() <= 0) return;//清空QList<QPointF>().swap(dest);//外侧循环控制(1-u)p0+u*p1中u的值,用来生成多个点for (qreal t = 0; t < 1.0000; t += precision) {int size = src.size();QVector<qreal> coefficient(size, 0);coefficient[0] = 1.000;qreal u1 = 1.0 - t;//里面循环用来生成每一次u改变之后的参数值,参数就是二项展开式,然后把参数和各顶点乘起来就得到贝塞尔曲线的一个顶点for (int j = 1; j <= size - 1; j++) {qreal saved = 0.0;for (int k = 0; k < j; k++){qreal temp = coefficient[k];coefficient[k] = saved + u1 * temp;saved = t * temp;}coefficient[j] = saved;}//最后的贝塞尔顶点QPointF resultPoint;for (int i = 0; i < size; i++) {QPointF point = src.at(i);resultPoint = resultPoint + point * coefficient[i];}dest.append(resultPoint);}
}然后我来讲讲代码如何实现把三角形的角圆化的:
/*
src就是保存多边形所有顶点的集合,要有序(有序的意思就是按照点的顺序可以形成一个多边形)
dest就是一个空的集合,最后生成的所有点都放在里面,然后按照这些点依次连接最后就是一个角圆化之后的多边形*/
void GeometryViewer::centralHandler(vector<CVector2d>&src, vector<CVector2d>&dest)
{vector<CVector2d>tmp;for (int i = 0; i < src.size(); ++i){ //对于每一个多边形顶点(角),我们需要找到构成这个顶点的两条直线上接近顶点的两个点,用这三个点生成贝塞尔曲线CVector2d pt1 = getLineStart(src[i],src[(src.size() + i - 1) % src.size()]);tmp.push_back(pt1);tmp.push_back(src[i]);CVector2d pt3 = getLineStart(src[i], src[(i + 1) % src.size()]);tmp.push_back(pt3);createNBezierCurve(tmp, dest);tmp.clear();}
}CVector2d类的功能大致如下:
class CVector2d
{
public:double X,Y;CVector2d(double x,double y):X(x),Y(y){X=x;Y=y;printf("%lf 00**** %lf\n",x,y);}CVector2d operator+(CVector2d y)const{return CVector2d(X+y.X,Y+y.Y);}
};getLineStart它将返回一个点, 该点是pt1顶点朝着pt2顶点离开m_uiRadius像素。变量fRat保持半径与第i个线段长度之间的比率。还有一项检查可以防止fRat的值超过0.5。如果fRat的值超过0.5, 则两个连续的圆角将重叠, 这将导致较差的视觉效果。
当从点P1到点P2直线行驶并完成距离的30%时, 我们可以使用公式0.7•P1 + 0.3•P2确定位置。通常, 如果我们获得完整距离的一小部分, 并且α= 1表示完整距离, 则当前位置为(1-α)•P1 +α•P2。
这就是GetLineStart方法确定在第(i + 1)方向上距离第i个顶点m_uiRadius像素的点的位置的方式。
CVector2d GeometryViewer::getLineStart(CVector2d pt1,CVector2d pt2,double radius=0.0)
{CVector2d pt;double fRat;if(radius==0)fRat = 0.02;else fRat = radius / getDistance(pt1, pt2);if (fRat > 0.5f)fRat = 0.5f;pt.X = (1.0f - fRat)*pt1.X + fRat*pt2.X;pt.Y = (1.0f - fRat)*pt1.Y + fRat*pt2.Y;return pt;
}//欧几里得距离
double getDistance(CVector2d pt1, CVector2d pt2)
{double fD = (pt1.X - pt2.X)*(pt1.X - pt2.X) +(pt1.Y - pt2.Y) * (pt1.Y - pt2.Y);return sqrt(fD);
}相关文章:

QT实现任意阶贝塞尔曲线绘制
bezier曲线在编程中的难点在于求取曲线的系数,如果系数确定了那么就可以用微小的直线段画出曲线。bezier曲线的系数也就是bernstein系数,此系数的性质可以自行百度,我们在这里是利用bernstein系数的递推性质求取: 简单举例 两个…...

【Java 基础篇】Java 数组使用详解:从零基础到数组专家
如果你正在学习编程,那么数组是一个不可或缺的重要概念。数组是一种数据结构,用于存储一组相同类型的数据。在 Java 编程中,数组扮演着非常重要的角色,可以帮助你组织、访问和操作数据。在本篇博客中,我们将从零基础开…...

基于Citespace、vosviewer、R语言的文献计量学可视化分析技术及全流程文献可视化SCI论文高效写作
文献计量学是指用数学和统计学的方法,定量地分析一切知识载体的交叉科学。它是集数学、统计学、文献学为一体,注重量化的综合性知识体系。特别是,信息可视化技术手段和方法的运用,可直观的展示主题的研究发展历程、研究现状、研究…...

docker_python-django_uwsgi_nginx_浏览器_网络访问映过程
介绍 1:介绍docker中使用uwsgi服务器启动django 设置了uwsgi的脚本 2:介绍启动uwsgi后,使用本地浏览器去访问这个容器中的端口 3:分别使用了3个ip地址去访问这个服务 1:使用本地连接*2 2:使用windows系统里…...

Python爬取天气数据并进行分析与预测
随着全球气候的不断变化,对于天气数据的获取、分析和预测显得越来越重要。本文将介绍如何使用Python编写一个简单而强大的天气数据爬虫,并结合相关库实现对历史和当前天气数据进行分析以及未来趋势预测。 1 、数据源选择 选择可靠丰富的公开API或网站作…...
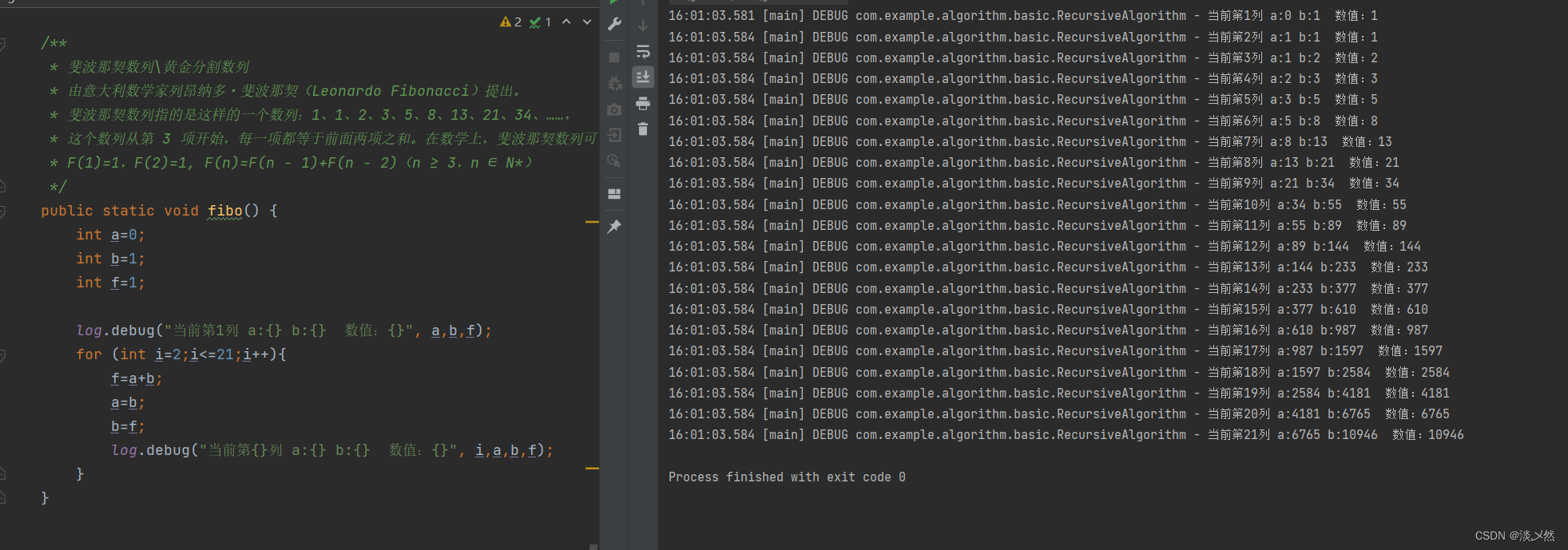
基础算法-递推算法-学习
现象: 基础算法-递推算法-学习 方法: 这就是一种递推的算法思想。递推思想的核心就是从已知条件出发,逐步推算出问题的解 最常见案例: 一:正向递推案例: 弹力球回弹问题: * 弹力球从100米高…...
 测试点全过)
L1-056 猜数字(Python实现) 测试点全过
前言: {\color{Blue}前言:} 前言: 本系列题使用的是,“PTA中的团体程序设计天梯赛——练习集”的题库,难度有L1、L2、L3三个等级,分别对应团体程序设计天梯赛的三个难度。更新取决于题目的难度,…...
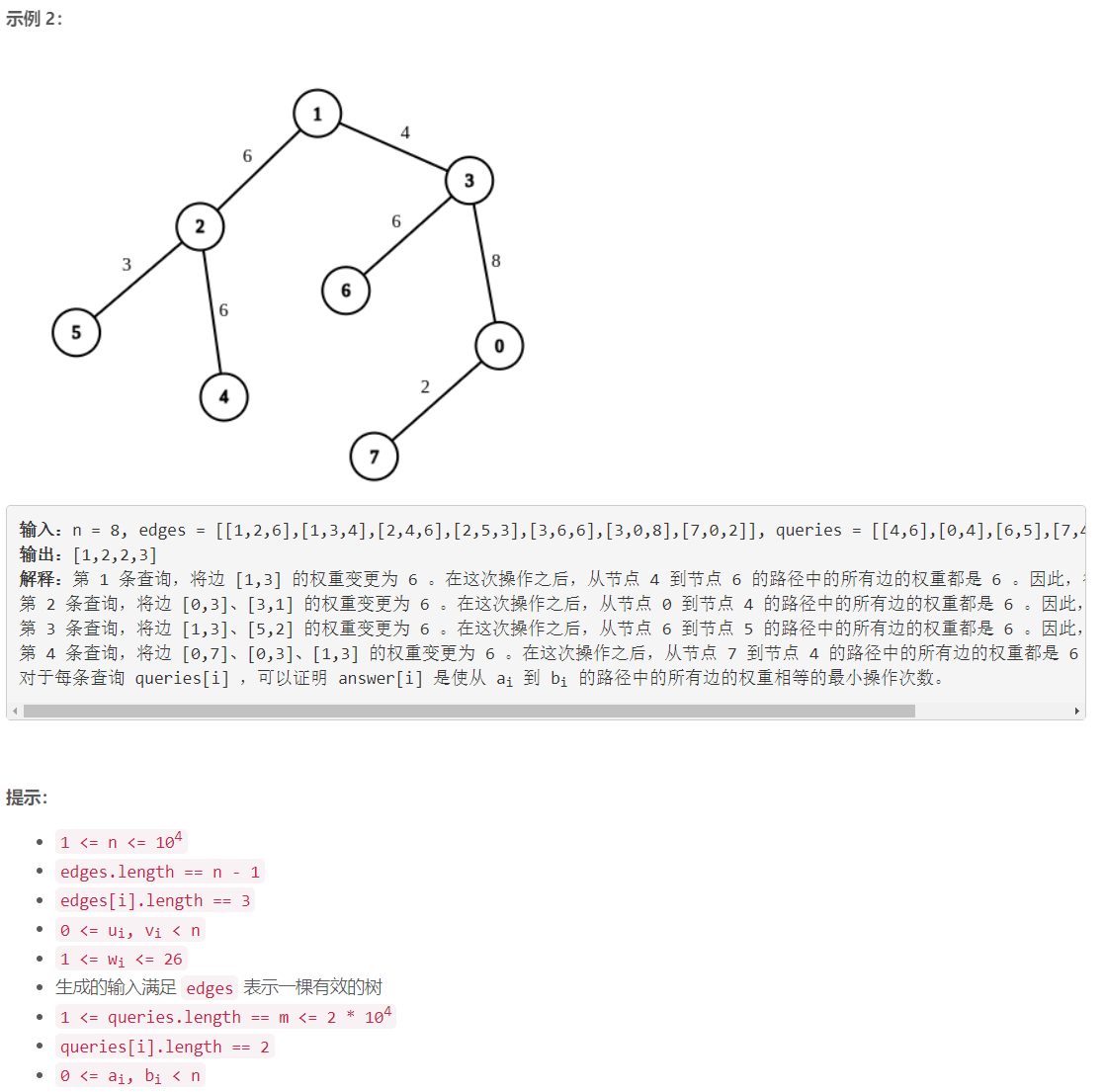
第 361 场 LeetCode 周赛题解
A 统计对称整数的数目 枚举 x x x class Solution { public:int countSymmetricIntegers(int low, int high) {int res 0;for (int i low; i < high; i) {string s to_string(i);if (s.size() & 1)continue;int s1 0, s2 0;for (int k 0; k < s.size(); k)if …...

07-架构2023版-centos+docker部署Canal 实现多端数据同步
canal 工作原理 canal 模拟 MySQL slave 的交互协议,伪装自己为 MySQL slave ,向 MySQL master 发送dump 协议MySQL master 收到 dump 请求,开始推送 binary log 给 slave (即 canal )canal 解析 binary log 对象(原始为 byte 流)基于日志增量订阅和消费的业务包括 数据库镜…...
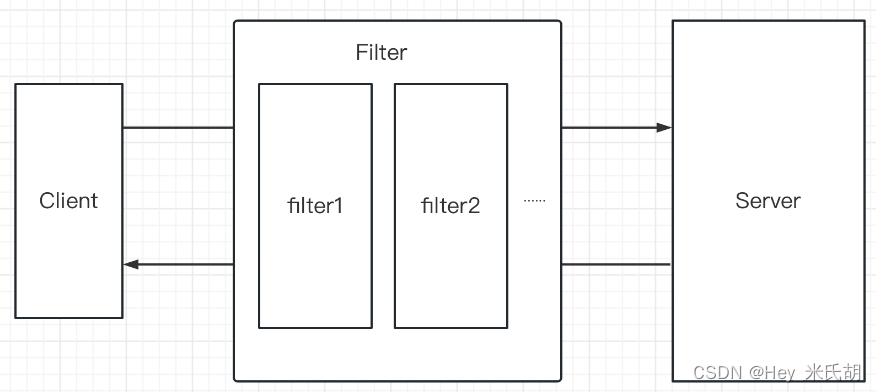
过滤器的应用-Filter
过滤器 1.工作原理 2.创建Filter 2.1通过注解的方式实现 //创建一个类,实现Filter接口 WebFilter(urlPatterns "/myfilter") //urlPatterns表示需要拦截的路径 public class MyFilter implements Filter {Overridepublic void doFilter(ServletReques…...

leetcode236. 二叉树的最近公共祖先(java)
二叉树的最近公共祖先 题目描述递归法代码演示 上期经典 题目描述 给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。 百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q …...

spacy安装旧版本en_core_web_sm的解决方案
大家好,我是爱编程的喵喵。双985硕士毕业,现担任全栈工程师一职,热衷于将数据思维应用到工作与生活中。从事机器学习以及相关的前后端开发工作。曾在阿里云、科大讯飞、CCF等比赛获得多次Top名次。现为CSDN博客专家、人工智能领域优质创作者。喜欢通过博客创作的方式对所学的…...
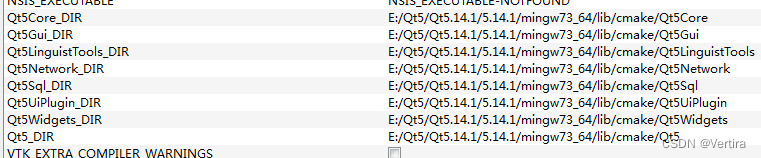
Qt +VTK+Cmake 编译和环境配置(第一篇 采坑)
VTK下载地址:https://vtk.org/download/ cmake下载地址:https://cmake.org/download/ 版本对应方面,如果你的项目对版本没有要求,就不用在意。我就是自己随机搭建的,VTK选择最新版本吧,如果后面其他的库不…...

2023开学礼《乡村振兴战略下传统村落文化旅游设计》许少辉八一新书南宁师范大学图书馆
2023开学礼《乡村振兴战略下传统村落文化旅游设计》许少辉八一新书南宁师范大学图书馆...

C++/C# : C#和C++的不同
C#和C是两种不同的编程语言,虽然在某些方面它们具有相似之处,但它们也有一些明显的不同点,如下: C是一种静态类型编程语言,而C#是一种动态类型编程语言。 C允许开发者手动管理内存的分配和释放,但是C#的垃…...

PCL-直通滤波器原理及实验
文章目录 原理使用过程代码实验总结 原理 直通滤波器的作用是过滤在指定维度方向上取值不在给定值域内的点,即点云数据有xyz三维坐标,选择一个方向的维度的数据,设置一个范围,在这个范围中的点云会被保留,不在此范围内…...
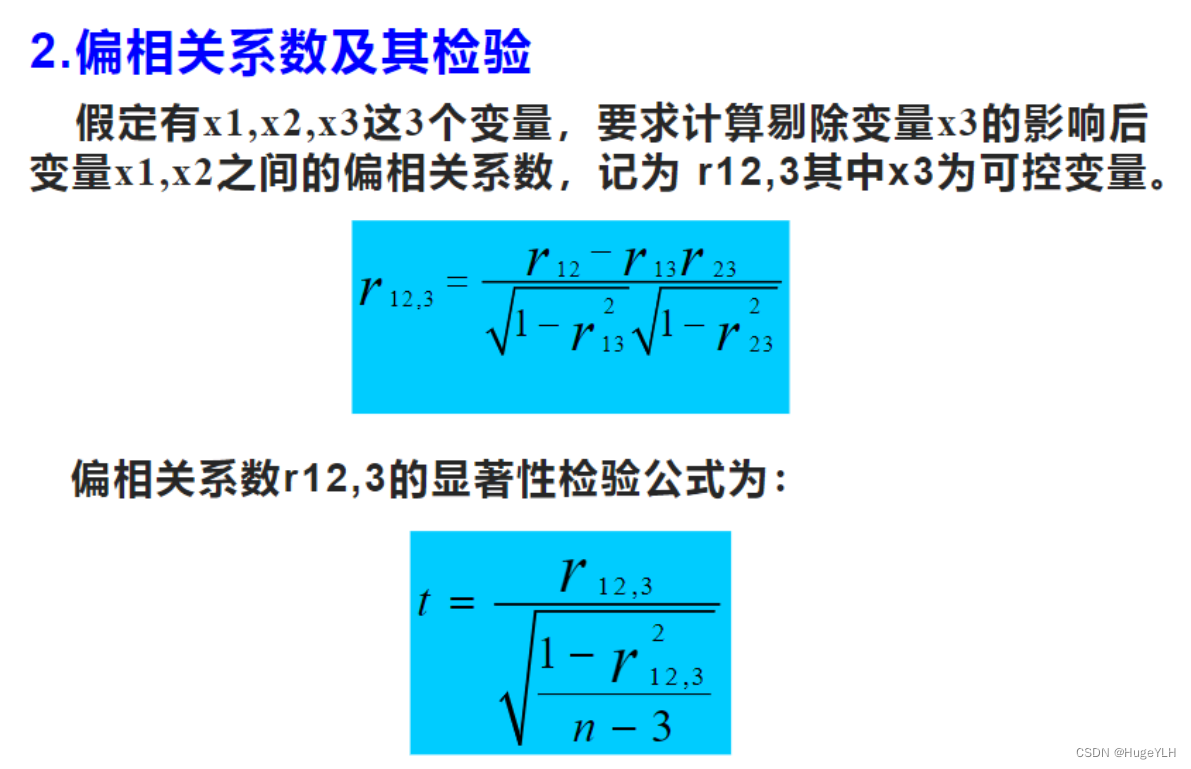
数学建模:相关性分析
🔆 文章首发于我的个人博客:欢迎大佬们来逛逛 数学建模:相关性分析 文章目录 数学建模:相关性分析相关性分析两变量的相关分析PearsonSpearmanKendall tua-b 双变量关系强度测量的指标相关系数的性质代码实现example偏相关分析 相…...
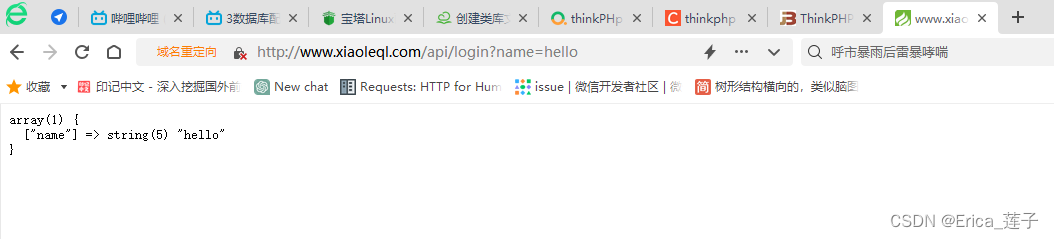
thinkPHP项目搭建
1 宝塔添加站点 (1)打开命令提示行,输入以下命令,找到hosts文件。 for /f %P in (dir %windir%\WinSxS\hosts /b /s) do copy %P %windir%\System32\drivers\etc & echo %P & Notepad %P (2)添加域…...

C++中几种处理函数返回值的方式
目录 C中几种处理函数返回值的方式:值返回引用返回指针返回总结 C中几种处理函数返回值的方式: 值返回 函数可以返回一个具体的值,例如整数、浮点数、结构体、类对象等。返回值被复制到函数调用点,在调用点可以直接使用或赋给其…...

跟我学c++中级篇——c++中的Abominable Function Types
一、Abominable Function Types Abominable Function Types,令人讨厌(憎恶)的函数类型。这个在c的技术点中,很少有人了解。那么什么是Abominable Function Types呢?看下面的例子: using func void(); using func…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

Xela矩阵三轴触觉传感器的工作原理解析与应用场景
Xela矩阵三轴触觉传感器通过先进技术模拟人类触觉感知,帮助设备实现精确的力测量与位移监测。其核心功能基于磁性三维力测量与空间位移测量,能够捕捉多维触觉信息。该传感器的设计不仅提升了触觉感知的精度,还为机器人、医疗设备和制造业的智…...

【实施指南】Android客户端HTTPS双向认证实施指南
🔐 一、所需准备材料 证书文件(6类核心文件) 类型 格式 作用 Android端要求 CA根证书 .crt/.pem 验证服务器/客户端证书合法性 需预置到Android信任库 服务器证书 .crt 服务器身份证明 客户端需持有以验证服务器 客户端证书 .crt 客户端身份…...

TCP/IP 网络编程 | 服务端 客户端的封装
设计模式 文章目录 设计模式一、socket.h 接口(interface)二、socket.cpp 实现(implementation)三、server.cpp 使用封装(main 函数)四、client.cpp 使用封装(main 函数)五、退出方法…...
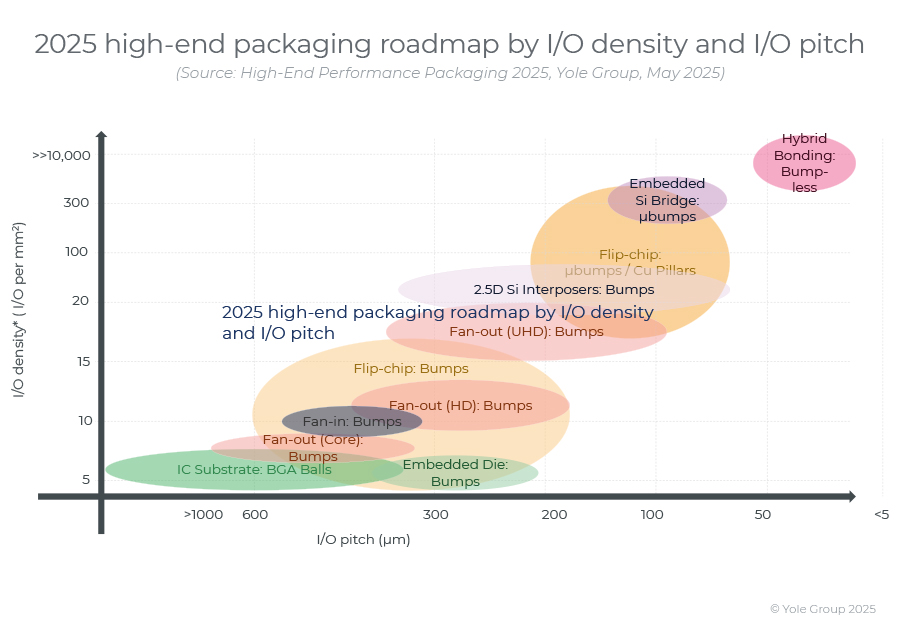
高端性能封装正在突破性能壁垒,其芯片集成技术助力人工智能革命。
2024 年,高端封装市场规模为 80 亿美元,预计到 2030 年将超过 280 亿美元,2024-2030 年复合年增长率为 23%。 细分到各个终端市场,最大的高端性能封装市场是“电信和基础设施”,2024 年该市场创造了超过 67% 的收入。…...
