【LeetCode题目详解】第九章 动态规划part02 62.不同路径 63. 不同路径 II day39补
本文章代码以c++为例!
一、力扣第62题:不同路径
题目:
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
示例 1:
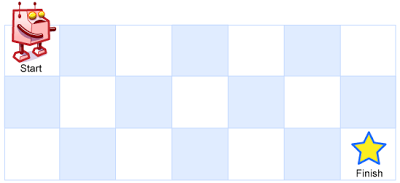
输入:m = 3, n = 7 输出:28
示例 2:
输入:m = 3, n = 2 输出:3 解释: 从左上角开始,总共有 3 条路径可以到达右下角。 1. 向右 -> 向下 -> 向下 2. 向下 -> 向下 -> 向右 3. 向下 -> 向右 -> 向下
示例 3:
输入:m = 7, n = 3 输出:28
示例 4:
输入:m = 3, n = 3 输出:6
提示:
1 <= m, n <= 100- 题目数据保证答案小于等于
2 * 109
思路
# 深搜
这道题目,刚一看最直观的想法就是用图论里的深搜,来枚举出来有多少种路径。
注意题目中说机器人每次只能向下或者向右移动一步,那么其实机器人走过的路径可以抽象为一棵二叉树,而叶子节点就是终点!
如图举例:
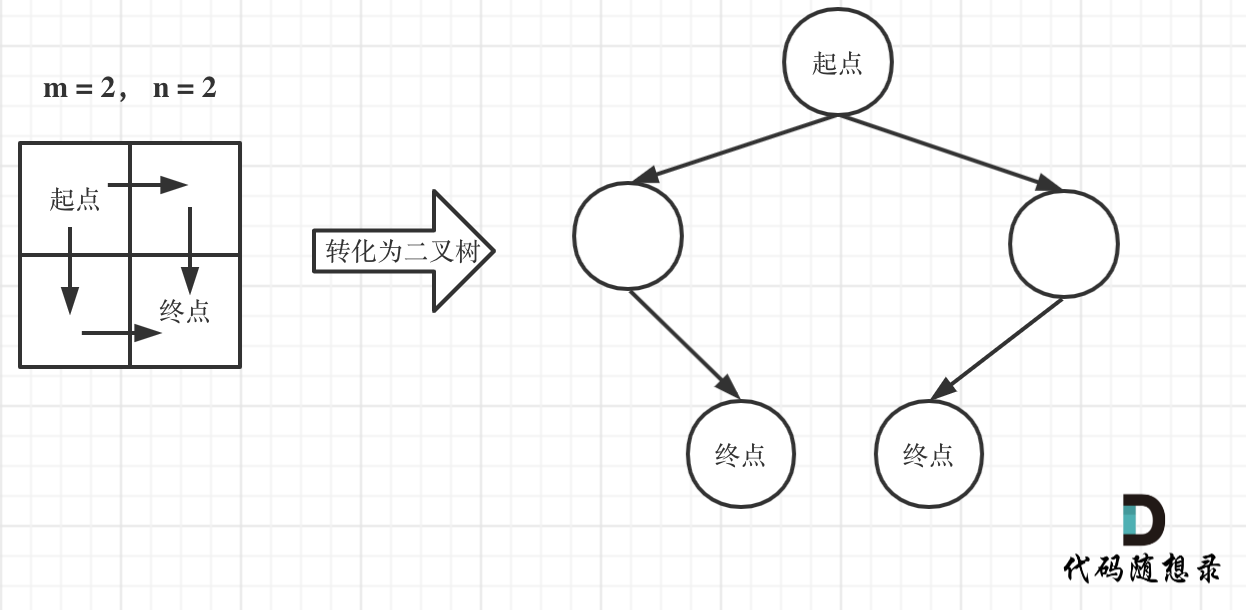
此时问题就可以转化为求二叉树叶子节点的个数,代码如下:
class Solution {
private:int dfs(int i, int j, int m, int n) {if (i > m || j > n) return 0; // 越界了if (i == m && j == n) return 1; // 找到一种方法,相当于找到了叶子节点return dfs(i + 1, j, m, n) + dfs(i, j + 1, m, n);}
public:int uniquePaths(int m, int n) {return dfs(1, 1, m, n);}
};
大家如果提交了代码就会发现超时了!
来分析一下时间复杂度,这个深搜的算法,其实就是要遍历整个二叉树。
这棵树的深度其实就是m+n-1(深度按从1开始计算)。
那二叉树的节点个数就是 2^(m + n - 1) - 1。可以理解深搜的算法就是遍历了整个满二叉树(其实没有遍历整个满二叉树,只是近似而已)
所以上面深搜代码的时间复杂度为O(2^(m + n - 1) - 1),可以看出,这是指数级别的时间复杂度,是非常大的。
# 动态规划
机器人从(0 , 0) 位置出发,到(m - 1, n - 1)终点。
按照动规五部曲来分析:
- 确定dp数组(dp table)以及下标的含义
dp[i][j] :表示从(0 ,0)出发,到(i, j) 有dp[i][j]条不同的路径。
- 确定递推公式
想要求dp[i][j],只能有两个方向来推导出来,即dp[i - 1][j] 和 dp[i][j - 1]。
此时在回顾一下 dp[i - 1][j] 表示啥,是从(0, 0)的位置到(i - 1, j)有几条路径,dp[i][j - 1]同理。
那么很自然,dp[i][j] = dp[i - 1][j] + dp[i][j - 1],因为dp[i][j]只有这两个方向过来。
- dp数组的初始化
如何初始化呢,首先dp[i][0]一定都是1,因为从(0, 0)的位置到(i, 0)的路径只有一条,那么dp[0][j]也同理。
所以初始化代码为:
for (int i = 0; i < m; i++) dp[i][0] = 1;
for (int j = 0; j < n; j++) dp[0][j] = 1;
- 确定遍历顺序
这里要看一下递推公式dp[i][j] = dp[i - 1][j] + dp[i][j - 1],dp[i][j]都是从其上方和左方推导而来,那么从左到右一层一层遍历就可以了。
这样就可以保证推导dp[i][j]的时候,dp[i - 1][j] 和 dp[i][j - 1]一定是有数值的。
- 举例推导dp数组
如图所示:
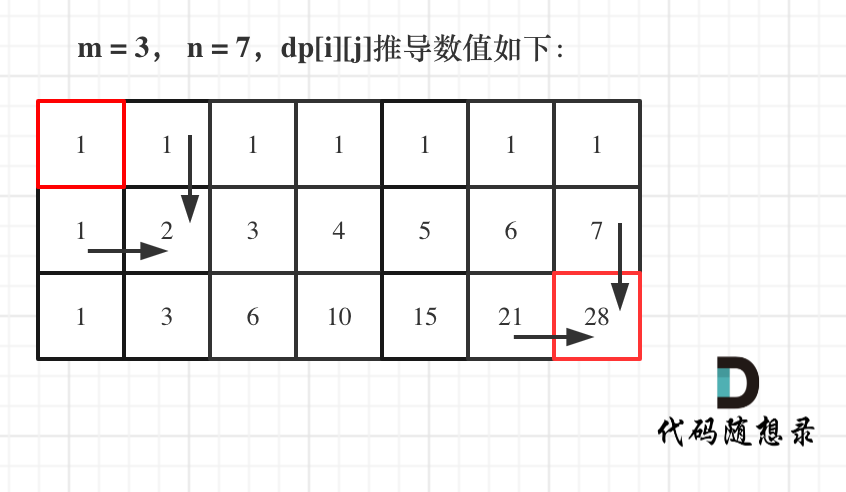
以上动规五部曲分析完毕,C++代码如下:
class Solution {
public:int uniquePaths(int m, int n) {vector<vector<int>> dp(m, vector<int>(n, 0));for (int i = 0; i < m; i++) dp[i][0] = 1;for (int j = 0; j < n; j++) dp[0][j] = 1;for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}}return dp[m - 1][n - 1];}
};
- 时间复杂度:O(m × n)
- 空间复杂度:O(m × n)
其实用一个一维数组(也可以理解是滚动数组)就可以了,但是不利于理解,可以优化点空间,建议先理解了二维,在理解一维,C++代码如下:
class Solution {
public:int uniquePaths(int m, int n) {vector<int> dp(n);for (int i = 0; i < n; i++) dp[i] = 1;for (int j = 1; j < m; j++) {for (int i = 1; i < n; i++) {dp[i] += dp[i - 1];}}return dp[n - 1];}
};
- 时间复杂度:O(m × n)
- 空间复杂度:O(n)
# 数论方法
在这个图中,可以看出一共m,n的话,无论怎么走,走到终点都需要 m + n - 2 步。

在这m + n - 2 步中,一定有 m - 1 步是要向下走的,不用管什么时候向下走。
那么有几种走法呢? 可以转化为,给你m + n - 2个不同的数,随便取m - 1个数,有几种取法。
那么这就是一个组合问题了。
那么答案,如图所示:
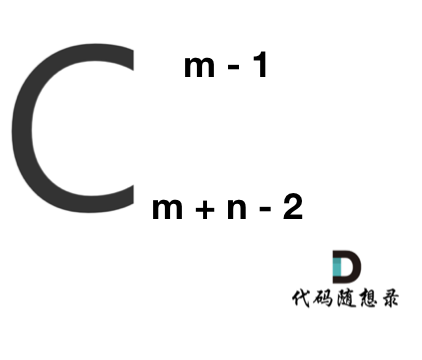
求组合的时候,要防止两个int相乘溢出! 所以不能把算式的分子都算出来,分母都算出来再做除法。
例如如下代码是不行的。
class Solution {
public:int uniquePaths(int m, int n) {int numerator = 1, denominator = 1;int count = m - 1;int t = m + n - 2;while (count--) numerator *= (t--); // 计算分子,此时分子就会溢出for (int i = 1; i <= m - 1; i++) denominator *= i; // 计算分母return numerator / denominator;}
};需要在计算分子的时候,不断除以分母,代码如下:
class Solution {
public:int uniquePaths(int m, int n) {long long numerator = 1; // 分子int denominator = m - 1; // 分母int count = m - 1;int t = m + n - 2;while (count--) {numerator *= (t--);while (denominator != 0 && numerator % denominator == 0) {numerator /= denominator;denominator--;}}return numerator;}
};
- 时间复杂度:O(m)
- 空间复杂度:O(1)
计算组合问题的代码还是有难度的,特别是处理溢出的情况!
# 总结
本文分别给出了深搜,动规,数论三种方法。
深搜当然是超时了,顺便分析了一下使用深搜的时间复杂度,就可以看出为什么超时了。
然后在给出动规的方法,依然是使用动规五部曲,这次我们就要考虑如何正确的初始化了,初始化和遍历顺序其实也很重要!
二、力扣第63题:不同路径 II
题目:
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
网格中的障碍物和空位置分别用 1 和 0 来表示。
示例 1:

输入:obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出:2
解释:3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径:
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右
示例 2:

输入:obstacleGrid = [[0,1],[0,0]] 输出:1
提示:
m == obstacleGrid.lengthn == obstacleGrid[i].length1 <= m, n <= 100obstacleGrid[i][j]为0或1
思路
这道题相对于62.不同路径
(opens new window) 就是有了障碍。
第一次接触这种题目的同学可能会有点懵,这有障碍了,应该怎么算呢?
62.不同路径
(opens new window)中我们已经详细分析了没有障碍的情况,有障碍的话,其实就是标记对应的dp table(dp数组)保持初始值(0)就可以了。
动规五部曲:
- 确定dp数组(dp table)以及下标的含义
dp[i][j] :表示从(0 ,0)出发,到(i, j) 有dp[i][j]条不同的路径。
- 确定递推公式
递推公式和62.不同路径一样,dp[i][j] = dp[i - 1][j] + dp[i][j - 1]。
但这里需要注意一点,因为有了障碍,(i, j)如果就是障碍的话应该就保持初始状态(初始状态为0)。
所以代码为:
if (obstacleGrid[i][j] == 0) { // 当(i, j)没有障碍的时候,再推导dp[i][j]dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
- dp数组如何初始化
在62.不同路径
(opens new window)不同路径中我们给出如下的初始化:
vector<vector<int>> dp(m, vector<int>(n, 0)); // 初始值为0
for (int i = 0; i < m; i++) dp[i][0] = 1;
for (int j = 0; j < n; j++) dp[0][j] = 1;
因为从(0, 0)的位置到(i, 0)的路径只有一条,所以dp[i][0]一定为1,dp[0][j]也同理。
但如果(i, 0) 这条边有了障碍之后,障碍之后(包括障碍)都是走不到的位置了,所以障碍之后的dp[i][0]应该还是初始值0。
如图:
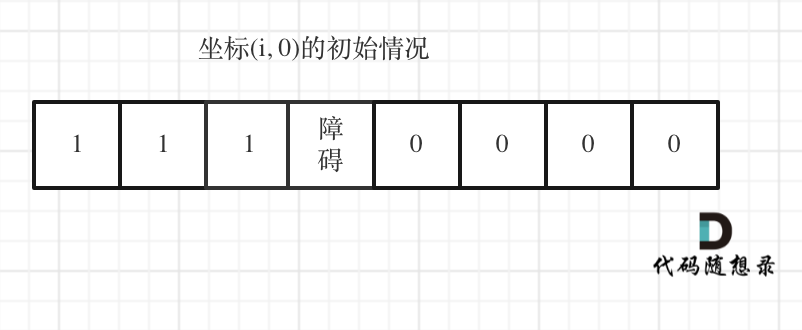
下标(0, j)的初始化情况同理。
所以本题初始化代码为:
vector<vector<int>> dp(m, vector<int>(n, 0));
for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;
for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) dp[0][j] = 1;
注意代码里for循环的终止条件,一旦遇到obstacleGrid[i][0] == 1的情况就停止dp[i][0]的赋值1的操作,dp[0][j]同理
- 确定遍历顺序
从递归公式dp[i][j] = dp[i - 1][j] + dp[i][j - 1] 中可以看出,一定是从左到右一层一层遍历,这样保证推导dp[i][j]的时候,dp[i - 1][j] 和 dp[i][j - 1]一定是有数值。
代码如下:
for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {if (obstacleGrid[i][j] == 1) continue;dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}
}
- 举例推导dp数组
拿示例1来举例如题:
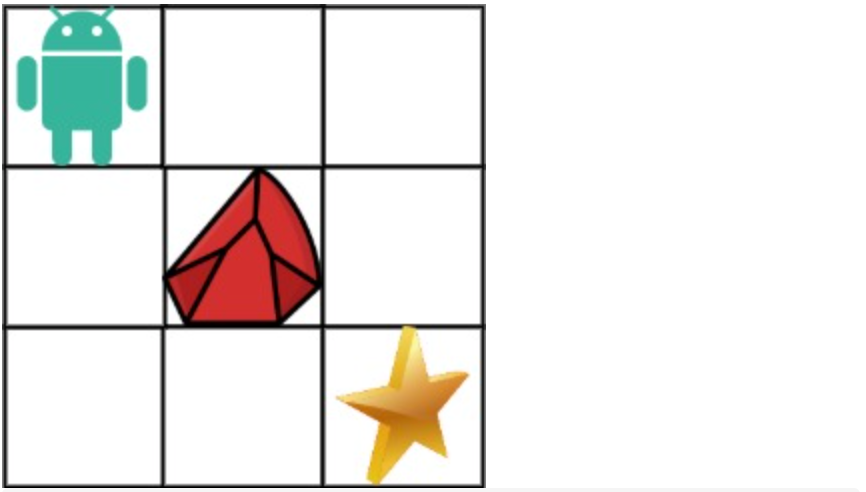
对应的dp table 如图:
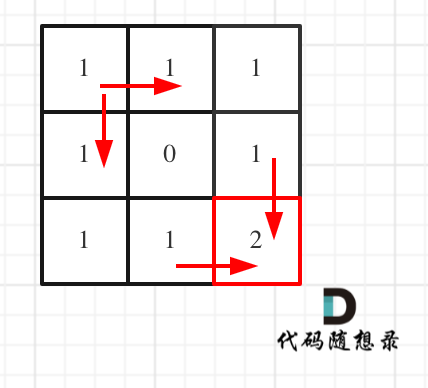
如果这个图看不懂,建议再理解一下递归公式,然后照着文章中说的遍历顺序,自己推导一下!
动规五部分分析完毕,对应C++代码如下:
class Solution {
public:int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {int m = obstacleGrid.size();int n = obstacleGrid[0].size();if (obstacleGrid[m - 1][n - 1] == 1 || obstacleGrid[0][0] == 1) //如果在起点或终点出现了障碍,直接返回0return 0;vector<vector<int>> dp(m, vector<int>(n, 0));for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) dp[0][j] = 1;for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {if (obstacleGrid[i][j] == 1) continue;dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}}return dp[m - 1][n - 1];}
};
- 时间复杂度:O(n × m),n、m 分别为obstacleGrid 长度和宽度
- 空间复杂度:O(n × m)
同样我们给出空间优化版本:
class Solution {
public:int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {if (obstacleGrid[0][0] == 1)return 0;vector<int> dp(obstacleGrid[0].size());for (int j = 0; j < dp.size(); ++j)if (obstacleGrid[0][j] == 1)dp[j] = 0;else if (j == 0)dp[j] = 1;elsedp[j] = dp[j-1];for (int i = 1; i < obstacleGrid.size(); ++i)for (int j = 0; j < dp.size(); ++j){if (obstacleGrid[i][j] == 1)dp[j] = 0;else if (j != 0)dp[j] = dp[j] + dp[j-1];}return dp.back();}
};
- 时间复杂度:O(n × m),n、m 分别为obstacleGrid 长度和宽度
- 空间复杂度:O(m)
# 总结
本题是62.不同路径
(opens new window)的障碍版,整体思路大体一致。
但就算是做过62.不同路径,在做本题也会有感觉遇到障碍无从下手。
其实只要考虑到,遇到障碍dp[i][j]保持0就可以了。
也有一些小细节,例如:初始化的部分,很容易忽略了障碍之后应该都是0的情况。
day39补
相关文章:

【LeetCode题目详解】第九章 动态规划part02 62.不同路径 63. 不同路径 II day39补
本文章代码以c为例! 一、力扣第62题:不同路径 题目: 一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。 机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(…...
四维轻云助力在线管理、展示及分享多种地理空间数据
《四维轻云》是一款轻量化的地理空间数据管理云平台,支持倾斜摄影模型、激光点云、数字高程模型及正射影像等多种地理空间数据的在线管理、展示及分享。目前,平台有项目管理、数据上传、场景搭建、发布分享、素材库等功能模块,支持多人在线协…...

CMake 学习笔记
一直想了解CMake,但是不知从何入门。最近看了CMake 官方的Tutorial,感觉的确很适合入门。 首先要安装CMake, 安装步骤: 直接去下载最新版Download | CMakemacos 点开CMake 后,遵循“How to Install For Command Line Use” 菜单项࿰…...
docker高级(DockerFile解析)
1、构建三步骤 编写Dockerfile文件 docker build命令构建镜像 docker run依镜像运行容器实例 2、DockerFile构建过程解析 Dockerfile内容基础知识 1:每条保留字指令都必须为大写字母且后面要跟随至少一个参数 2:指令按照从上到下,顺序执行…...

抽象类实现接口的意义
文章目录 前言一、抽象类和接口对比二、举例说明三种情况1.接口实现类接口 2.抽象类实现类抽象类实现类(子类) 3.抽象类实现接口接口抽象类三个实现类 总结 前言 抽象类和接口其实都是抽象的一种,那么他俩有何异同呢? 抽象类实现接口的意义何在? 一、抽象类和接口对比 接口…...

什么是接口测试,如何做接口测试?
比起点点点的功能测试,“接口测试”显得专业又高大上,也因此让有些初级测试人员“望而生畏”。别担心,其实接口测试也是功能测试的一种,它是针对接口进行的功能测试。 写在前面:本文参考了茹炳晟老师的《测试工程师 全…...
Keil 编译 Debug
# 头文件无法导入进来 # 导入头文件,只有函数声明,但缺少函数实现 已经导入了air32f10x_gpio.h但是没有导入 .c,就导致 编译出错出现undefined symbol (某个函数),这时候按照下面的操作,导入外设模块就好。...
【通用消息通知服务】0x3 - 发送我们第一条消息(Websocket)
【通用消息通知服务】0x3 - 发送我们第一条消息 项目地址: A generic message notification system[Github] 实现接收/发送Websocket消息 Websocket Connection Pool import asyncio from asyncio.queues import Queue from asyncio.queues import QueueEmpty from contextli…...
Eclipse打jar包与JavaDOC文档的生成
补充知识点——Eclipse打jar包与JavaDOC文档的生成 1、Eclipse如何打jar包,如何运行jar包 Java当中编写的Java代码,Java类、方法、接口这些东西就是项目中相关内容,到时候我们需要把代码提供给甲方、或者是我们需要运行我们编写的代码&…...
)
力扣:80. 删除有序数组中的重复项 II(Python3)
题目: 给你一个有序数组 nums ,请你 原地 删除重复出现的元素,使得出现次数超过两次的元素只出现两次 ,返回删除后数组的新长度。 不要使用额外的数组空间,你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下…...

linux:需要注意docker和aws的rds的mysql默认是UTC而不是中国时区
问题: 如题 解决办法: docker参考: mysql时间不对,修改时区_set global time_zone 无效_《小书生》的博客-CSDN博客 aws参考: https://www.youtube.com/watch?vB-NaqV-A1BY mysql - AWS修改RDS时区 - 个人文章 - Segm…...
访问 GitHub 方法
访问 GitHub 方法 方法一:最常见的就是 fq,但这个是违法的行为,自己私下搞可以,不能教你们。 方法二:利用加速器,这是正规合法操作。这里推荐一个免费的加速器,下载安装 Watt Toolkit加速器,原名…...
旅游APP外包开发注意事项
旅游类APP通常具有多种功能,以提供给用户更好的旅行体验。以下分享常见的旅游类APP功能以及在开发和使用这些APP时需要注意的问题,希望对大家有所帮助。北京木奇移动技术有限公司,专业的软件外包开发公司,欢迎交流合作。 常见功能…...
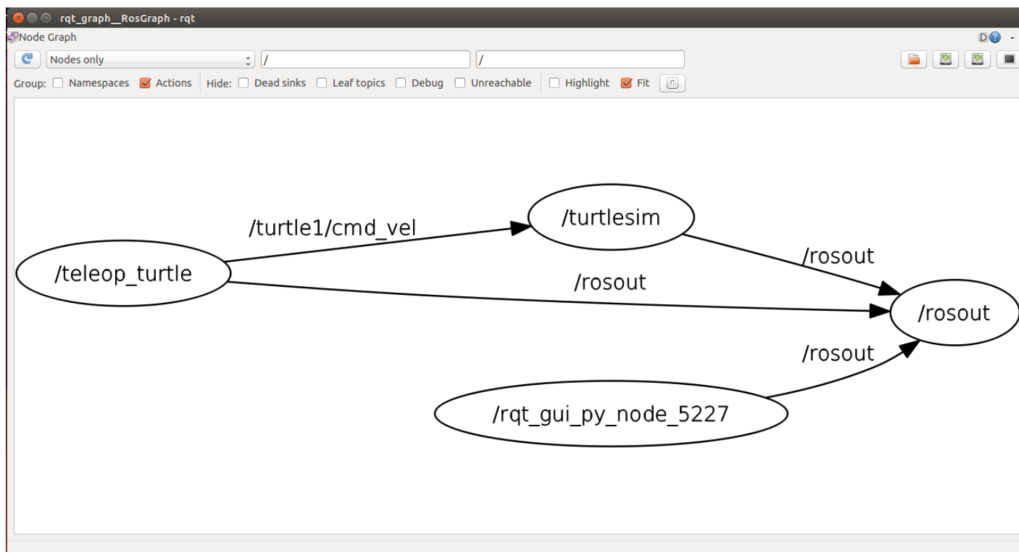
ROS机器人编程---------(二)ROS中的核心概念
ROS机器人编程 ROS中的核心概念 ROS的通信机制 在ROS中结点是最小单元,比如说机器人的遥控器可以作为一个控制结点,机器人上的摄像头也可以看作一个结点,ROS通过协调各个结点来实现 在启动任何ROS结点之前,都必须先启动ROS Mas…...

Python学习教程:进程的调度
前言 嗨喽~大家好呀,这里是魔王呐 ❤ ~! 要想多个进程交替运行,操作系统必须对这些进程进行调度, 这个调度也不是随即进行的,而是需要遵循一定的法则,由此就有了进程的调度算法。 python更多源码/资料/解答/教程等 …...
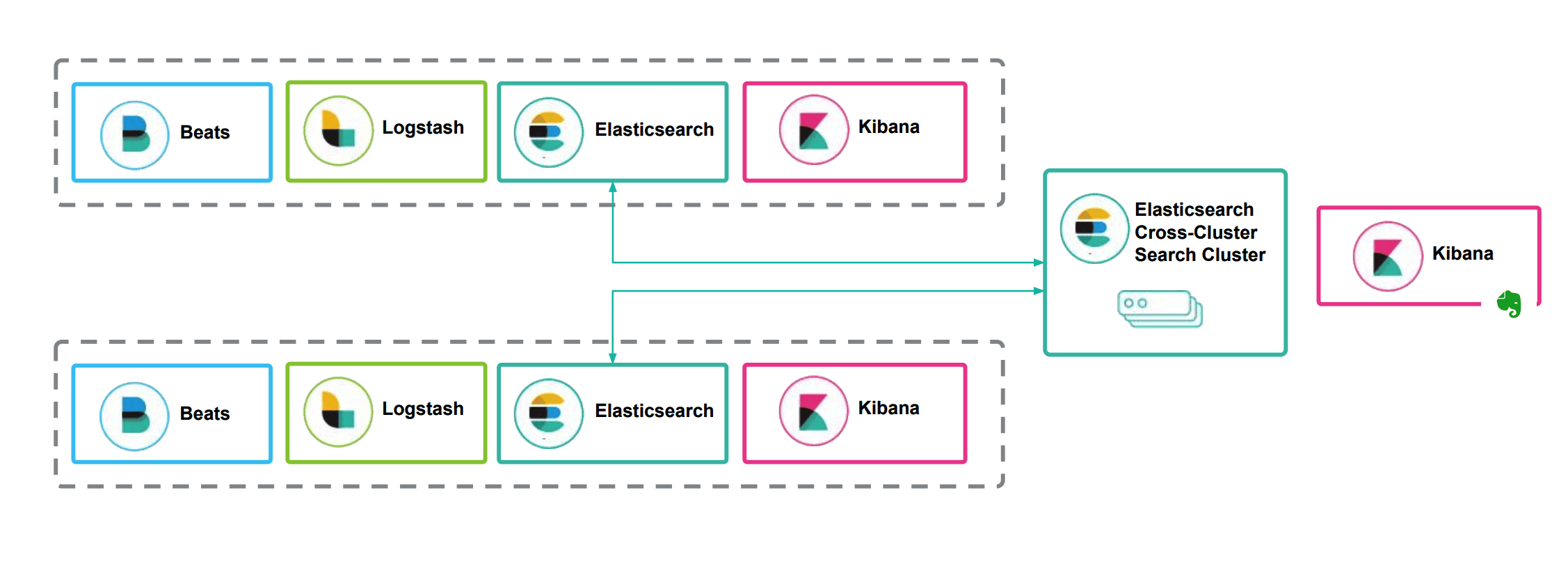
ElasticSearch第三讲:ES详解 - Elastic Stack生态和场景方案
ElasticSearch第三讲:ES详解 - Elastic Stack生态和场景方案 本文是ElasticSearch第三讲,在了解ElaticSearch之后,我们还要了解Elastic背后的生态 即我们常说的ELK;与此同时,还会给你展示ElasticSearch的案例场景&…...
基于Java+SpringBoot+Vue前后端分离农商对接系统设计和实现
博主介绍:✌全网粉丝30W,csdn特邀作者、博客专家、CSDN新星计划导师、Java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取源码联系🍅 👇🏻 精彩专…...
【模方ModelFun】实景三维建模和修模4.0.7最新版安装包以及图文安装教程
模方ModelFun 具有多种功能,旨在帮助用户进行实景三维建模和修模。以下是一些主要功能的简要介绍: 实景三维建模:【模方ModelFun】提供了自动化的实景三维重建功能,可以从实景图像中提取几何形状和纹理信息,生成高质量…...

介绍几个搜索引擎
Google:全球最大的搜索引擎,提供全面的搜索服务,包括网页、图片、视频、新闻、地图等。 Baidu:中国最大的搜索引擎,提供类似于Google的全面搜索服务,同时也有网盘、知道等功能。 Bing:微软公司…...
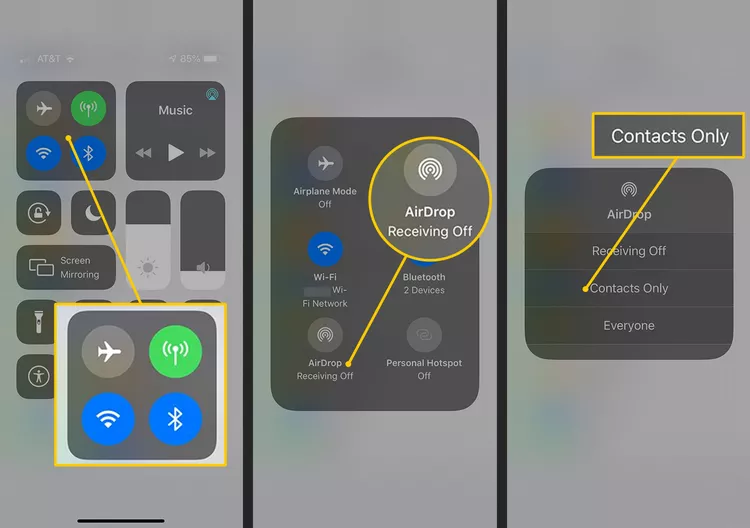
iPhone 隔空投送使用指南:详细教程
本文介绍了如何在iPhone上使用隔空投送,包括如何在iOS 11到iOS 14的iPhone上启用它、发送文件以及接受或拒绝AirDrop发送给你的文件。对于iOS 7以上的旧款iPhone,提供了另一种方法。 如何打开隔空投送 你可以通过以下两种方式之一启动隔空投送功能:在“设置”应用程序或控…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...
