[AGC043D] Merge Triplets
题目传送门
引
很有意思的计数题
解法
考虑经过操作后得到的排列的性质
性质1:
设 p r e ( i ) pre(i) pre(i):前i个位置的最大值,则不会出现超过3个的连续位置的 p r e pre pre相同
必要性:
考虑反证,若有超过 3 3 3个的连续位置的 p r e pre pre相同,那么至少有连续有连续三次选择了比第一次选择要小的数,那么至少一个块的长度为 4 4 4,题目中规定块长为 3 3 3,因此不合法
充分性:
发现没有充分性,比如: { 2 , 1 , 4 , 3 , 6 , 5 } \{2,1,4,3,6,5\} {2,1,4,3,6,5},手玩模拟一下就会发现有问题
性质2:
若排列总长为 3 N 3N 3N, i i i个的连续位置的 p r e pre pre相同的个数为 c n t i cnt_i cnti,那么 c n t 2 ≤ N − c n t 3 cnt_2\le N-cnt_3 cnt2≤N−cnt3
必要性:
对于 c n t 2 cnt_2 cnt2与 c n t 3 cnt_3 cnt3来说,他们对应的块内的大小关系是一定的,所以可得 c n t 2 + c n t 3 ≤ N cnt_2+cnt_3\le N cnt2+cnt3≤N,移项就行了
我们可以化简:
c n t 2 ≤ N − c n t 3 ⇒ 3 c n t 2 ≤ 3 N − 3 c n t 3 ⇒ 3 c n t 2 ≤ ( c n t 1 + 2 c n t 2 + 3 c n t 3 ) − 3 c n t 3 ⇒ 移项得 c n t 2 ≤ c n t 1 \begin{aligned} &cnt_2\le N-cnt_3\\ \Rightarrow&3cnt_2\le 3N-3cnt_3\\ \Rightarrow&3cnt_2\le (cnt_1+2cnt_2+3cnt_3)-3cnt_3\\ \Rightarrow^{移项得}&cnt_2\le cnt_1 \end{aligned} ⇒⇒⇒移项得cnt2≤N−cnt33cnt2≤3N−3cnt33cnt2≤(cnt1+2cnt2+3cnt3)−3cnt3cnt2≤cnt1
最后我们发现性质1和性质2加起来就有了充分性
状态设计:
f i , j : 前 i 个数, c n t 1 − c n t 2 = j 的方案数 f_{i,j}:前i个数,cnt_1-cnt_2=j的方案数 fi,j:前i个数,cnt1−cnt2=j的方案数
显然 a n s = ∑ k = 0 3 n f 3 n , k ans=\sum_{k=0}^{3n} f_{3n,k} ans=∑k=03nf3n,k
状态转移:
考虑从小到大放数,对放 1 / 2 / 3 1/2/3 1/2/3个数分别考虑
f i , j → f i + 1 , j + 1 f i , j → f i + 2 , j − 1 ∗ ( i − 1 ) f i , j → f i + 3 , j ∗ ( i − 1 ) ∗ ( i − 2 ) \begin{aligned} &f_{i,j}\to f_{i+1,j+1}\\ &f_{i,j}\to f_{i+2,j-1}*(i-1)\\ &f_{i,j}\to f_{i+3,j}*(i-1)*(i-2) \end{aligned} fi,j→fi+1,j+1fi,j→fi+2,j−1∗(i−1)fi,j→fi+3,j∗(i−1)∗(i−2)
就好了
code:
#include<bits/stdc++.h>
using namespace std;
const int N = 2e3 + 7, M = N * 3;
typedef long long ll;
int n,mod,ans;
int f[M][M<<1];
int ad(int x,int y){ return (1ll*x+1ll*y)%mod; }
void work(int i,int j){f[i+1][j+1+M]=ad(f[i+1][j+1+M],f[i][j+M]);f[i+2][j-1+M]=ad(f[i+2][j-1+M],1ll*f[i][j+M]*(i+1)%mod);f[i+3][j+M]=ad(f[i+3][j+M],1ll*f[i][j+M]*(i+1)%mod*(i+2)%mod);
}
int main() {scanf("%d%d",&n,&mod); n=n*3;f[0][M]=1;for(int i=0;i<n;i++) for(int j=-i;j<=i;j++) work(i,j);for(int i=0;i<=n;i++) ans=ad(ans,f[n][i+M]);printf("%d\n",ans);
}
TXL
相关文章:

[AGC043D] Merge Triplets
题目传送门 引 很有意思的计数题 解法 考虑经过操作后得到的排列的性质 性质1: 设 p r e ( i ) pre(i) pre(i):前i个位置的最大值,则不会出现超过3个的连续位置的 p r e pre pre相同 必要性: 考虑反证,若有超过 3 3 3个的连续…...

2023年人工智能开源项目前20名
推荐:使用 NSDT场景编辑器快速搭建3D应用场景 1. Tensorflow 2. Hugging Face Transformers 3. Opencv 4. Pytorch 5. Keras 6. Stable Diffusion 7. Deepfacelab 8. Detectron2 9. Apache Mxnet 10. Fastai 11. Open Assistant 12. Mindsdb 13. Dall E…...

ThinkPHP 集成 jwt 技术 token 验证
ThinkPHP 集成 jwt 技术 token 验证 一、思路流程二、安装 firebase/php-jwt三、封装token类四、创建中间件,检验Token校验时效性五、配置路由中间件六、写几个测试方法,通过postman去验证 一、思路流程 客户端使用用户名和密码请求登录服务端收到请求&…...
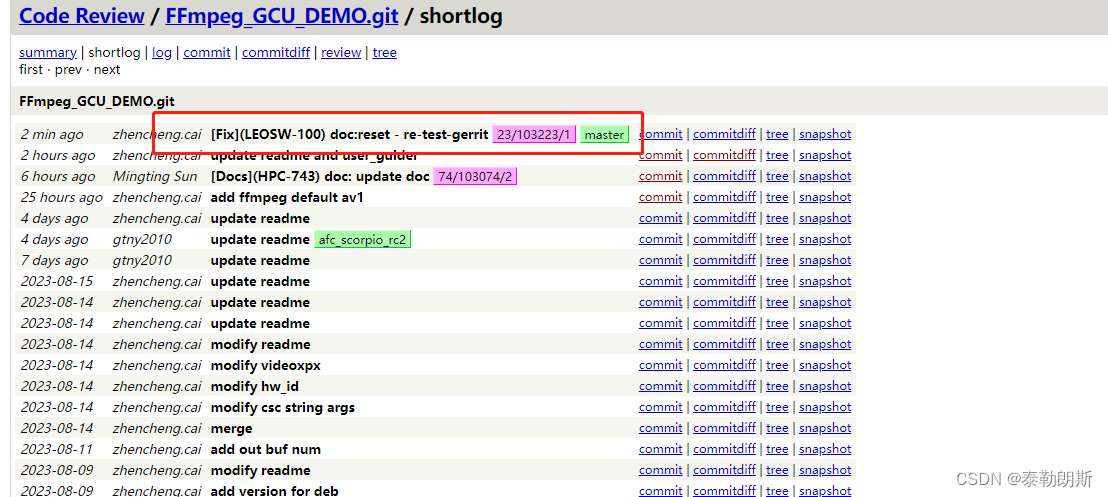
gerrit 如何提交进行review
前言 本文主要介绍如何使用gerrit进行review。 下述所有流程都是参考: https://gerrit-review.googlesource.com/Documentation/intro-gerrit-walkthrough.html 先给一个commit后但是还没有push上去的一个办法: git reset --hard HEAD^可以多次reset.…...

罗勇军 →《算法竞赛·快冲300题》每日一题:“游泳” ← DFS+剪枝
【题目来源】http://oj.ecustacm.cn/problem.php?id1753http://oj.ecustacm.cn/viewnews.php?id1023【题目描述】 游泳池可以等分为n行n列的小区域,每个区域的温度不同。 小明现在在要从游泳池的左上角(1, 1)游到右下角(n, n),小明只能向上下左右四个方…...

【教程】PyTorch Timer计时器
转载请注明出处:小锋学长生活大爆炸[xfxuezhang.cn] OpenCV的Timer计时器可以看这篇:Python Timer和TimerFPS计时工具类 Timer作用说明:统计某一段代码的运行耗时。 直接上代码,开箱即用。 import time import torch import os …...
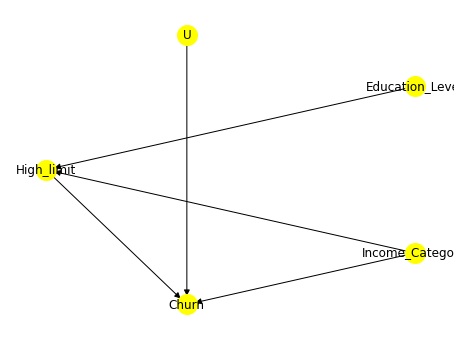
因果推断(六)基于微软框架dowhy的因果推断
因果推断(六)基于微软框架dowhy的因果推断 DoWhy 基于因果推断的两大框架构建:「图模型」与「潜在结果模型」。具体来说,其使用基于图的准则与 do-积分来对假设进行建模并识别出非参数化的因果效应;而在估计阶段则主要…...

探索隧道ip如何助力爬虫应用
在数据驱动的世界中,网络爬虫已成为获取大量信息的重要工具。然而,爬虫在抓取数据时可能会遇到一些挑战,如IP封禁、访问限制等。隧道ip(TunnelingProxy)作为一种强大的解决方案,可以帮助爬虫应用更高效地获…...

题目:2629.复合函数
题目来源: leetcode题目,网址:2629. 复合函数 - 力扣(LeetCode) 解题思路: 倒序遍历计算。 解题代码: /*** param {Function[]} functions* return {Function}*/ var compose function(…...

【实训项目】精点考研
1.设计摘要 如果说高考是一次能够改变命运的考试,那么考研应该是另外一次。为什么那么多人都要考研呢?从中国教育在线官方公布是考研动机调查来看,大家扎堆考研的原因大概集中在这6个方面:本科就业压力大,提升竞争力、…...

软件测试Pytest实现接口自动化应该如何在用例执行后打印日志到日志目录生成日志文件?
Pytest可以使用内置的logging模块来实现接口自动化测试用例执行后打印日志到日志目录以生成日志文件。以下是实现步骤: 1、在pytest配置文件(conftest.py)中,定义一个日志输出路径,并设置logging模块。 import loggi…...

深入理解作用域、作用域链和闭包
🎬 岸边的风:个人主页 🔥 个人专栏 :《 VUE 》 《 javaScript 》 ⛺️ 生活的理想,就是为了理想的生活 ! 目录 📚 前言 📘 1. 词法作用域 📖 1.2 示例 📖 1.3 词法作用域的…...

7款适合3D建模和渲染的GPU推荐
选择一款完美的 GPU 并不是一件容易的事;您不仅必须确保有特定数量的线程和内核来处理图像,而且还应该有足够的 RAM。 这是因为 3D 渲染是一个活跃的工作过程,因为您必须坐在 PC 前并持续与软件交互。为了在 3D 场景中积极工作,您…...

边缘计算物联网网关在机械加工行业的应用及作用分享
随着工业4.0的推进,物联网技术正在逐渐渗透到各个行业领域。机械加工行业作为制造业的基础领域之一,其生产过程的自动化、智能化水平直接影响到产品质量和生产效率。边缘计算物联网网关作为物联网技术的重要组成部分,在机械加工行业中发挥着越…...
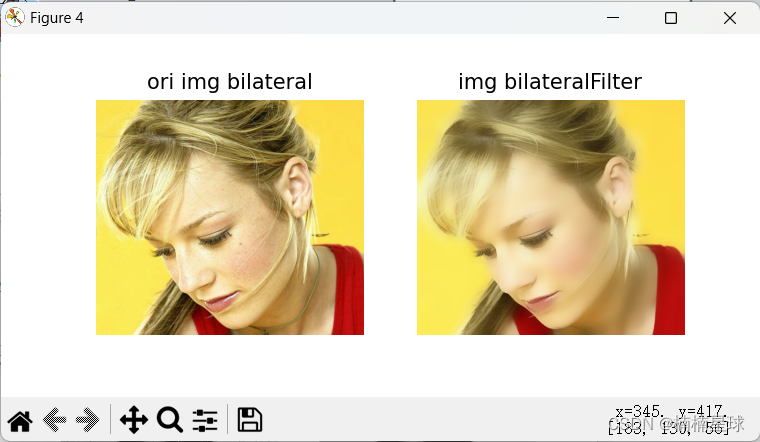
(笔记六)利用opencv进行图像滤波
(1)自定义卷积核图像滤波 import numpy as np import matplotlib.pyplot as plt import cv2 as cvimg_path r"D:\data\test6-6.png" img cv.imread(img_path)# 图像滤波 ker np.ones((6, 6), np.float32)/36 # 构建滤波器(卷积…...
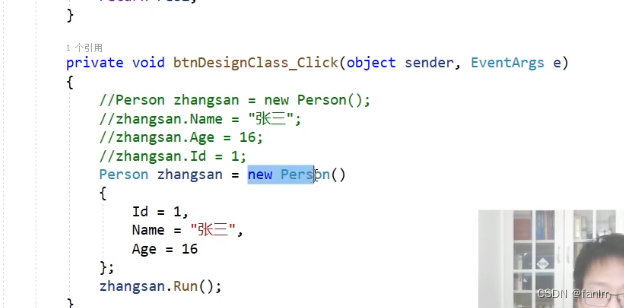
WPF C# .NET7 基础学习
学习视频地址:https://www.bilibili.com/video/BV1hx4y1G7C6?p3&vd_source986db470823ebc16fe0b3d235addf050 开发工具:Visual Studio 2022 Community 基础框架:.Net 6.0 下载创建过程略 .Net和.Framework 区别是Net是依赖项ÿ…...

QT里使用sqlite的问题,好多坑
1. 我使用sqlite,开发机上好好的,测试机上却不行。后来发现是缺少驱动(Driver not loaded Driver not loaded),代码检查了又检查,发现应该是缺少dll文件(系统不提示,是自己使用 QMes…...

openGauss学习笔记-59 openGauss 数据库管理-相关概念介绍
文章目录 openGauss学习笔记-59 openGauss 数据库管理-相关概念介绍59.1 数据库59.2 表空间59.3 模式59.4 用户和角色59.5 事务管理 openGauss学习笔记-59 openGauss 数据库管理-相关概念介绍 59.1 数据库 数据库用于管理各类数据对象,与其他数据库隔离。创建数据…...

Nginx安装与部署
文章目录 一,说明二,下载三,Windows下安装1,安装2,启动3,验证 四,Linux下安装1,安装2,启动3,验证 五,Nginx配置 一,说明 Nginx是一款高性能Web和反向代理服务器,提供内存少,高并发,负载均衡和反向代理服务,支持windos和linux系统 二,下载 打开浏览器,输入地址: https://ngin…...
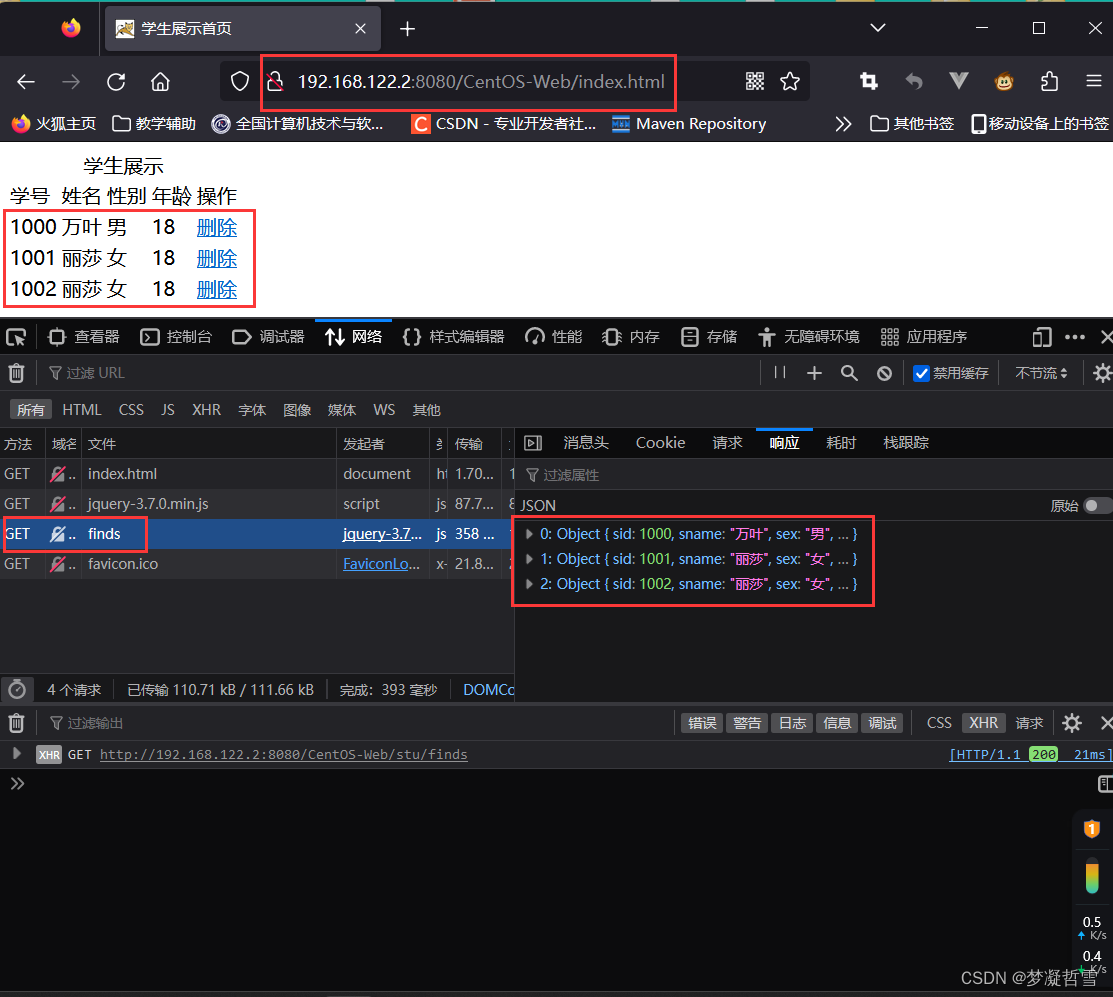
Linux中Tomcat发布war包后无法正常访问非静态资源
事故现象 在CentOS8中安装完WEB环境,首次部署WEB项目DEMO案例,发现可以静态的网页内容, 但是无法向后台发送异步请求,全部出现404问题,导致数据库数据无法渲染到界面上。 原因分析 CentOS请求中提示用来获取资源的连…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...
