支持向量机(二)
文章目录
- 前言
- 具体内容
前言
总算要对稍微有点难度的地方动手了,前面介绍的线性可分或者线性不可分的情况,都是使用平面作为分割面的,现在我们采用另一种分割面的设计方法,也就是核方法。
核方法涉及的分割面不再是 w x + b = 0 wx+b=0 wx+b=0,而是 f ( x ) = 0 f(x)=0 f(x)=0了。
具体内容
核方法其实就是坐标映射方法,类似于我们进行回归的时候对于反函数曲线采用 y = w x + b y=\frac{w}{x}+b y=xw+b的形式来对数据进行拟合。
我们常用的标准做法都是先将原始数据 x x x映射为 1 x \frac{1}{x} x1,然后对于数据 ( 1 x , y ) (\frac{1}{x},y) (x1,y)寻找线性函数 y = k t + b y=kt+b y=kt+b来拟合。
在非线性支持向量机中,我们需要把原始特征x通过映射函数变换为 ϕ ( x ) \phi(x) ϕ(x),对于这个映射函数没有什么要求,只不过什么样的映射函数映射以后分类效果最佳是未知的,是需要通过比较才能发现的。
映射函数一般都是把原始特征 x x x变为另一个向量 [ 1 , x 1 , ⋯ , x n , x 1 2 , ⋯ , x i x j , ⋯ , x n 2 , ⋯ ] [1,x_1,\cdots,x_n,x_1^2,\cdots,x_ix_j,\cdots,x_n^2,\cdots] [1,x1,⋯,xn,x12,⋯,xixj,⋯,xn2,⋯]其中的一项或者几项,具体是几项视具体情况确定,这个的目标是保留原始信息同时要增加尽可能多的生成信息,所以一般往高维方向映射。
当然这个函数设计好以后,我们在支持向量机的对偶函数中其实计算的是 K ( x i , x j ) K(x_i,x_j) K(xi,xj),这个函数是上面映射函数的乘积,可能计算更加复杂,所以从方便对偶函数的计算角度出发,设计了专门的对偶核函数,不过对偶核函数是有要求的,需要对所有特征 x x x所构成的gram矩阵是半正定的。
而这种情况下我们可以设计方便计算的核函数,比如:
多项式核函数: K ( x , z ) = ( x ⋅ z + 1 ) p K(x,z)=(x\cdot z+1)^p K(x,z)=(x⋅z+1)p,计算难度大大减小,而且这个多项式核函数对应的映射函数也比较好求:
K ( x , z ) = ( x ⋅ z + 1 ) 2 = ( x 1 z 1 + x 2 z 2 + 1 ) 2 = x 1 2 z 1 2 + 2 x 1 x 2 z 1 z 2 + 2 x 1 z 1 + x 2 2 z 2 2 + 2 x 2 z 2 + 1 = [ x 1 2 , 2 x 1 x 2 , 2 x 1 , x 2 2 , 2 x 2 , 1 ] ∗ [ z 1 2 , 2 z 1 z 2 , 2 z 1 , z 2 2 , 2 z 2 , 1 ] T \begin{align*} K(x,z)&=(x\cdot z+1)^2\\ &=(x_1z_1+x_2z_2+1)^2\\ &=x_1^2z_1^2+2x_1x_2z_1z_2+2x_1z_1+x_2^2z_2^2+2x_2z_2+1\\ &=[x_1^2,\sqrt{2}x_1x_2,\sqrt{2}x_1,x_2^2,\sqrt{2}x_2,1]*[z_1^2,\sqrt{2}z_1z_2,\sqrt{2}z_1,z_2^2,\sqrt{2}z_2,1]^T \end{align*} K(x,z)=(x⋅z+1)2=(x1z1+x2z2+1)2=x12z12+2x1x2z1z2+2x1z1+x22z22+2x2z2+1=[x12,2x1x2,2x1,x22,2x2,1]∗[z12,2z1z2,2z1,z22,2z2,1]T
相当于截取了泰勒展开式中的前几项。
换句话说,如果我们想将坐标映射为 [ 1 , x 1 , x 2 , x 1 2 , x 1 x 2 , x 2 2 ] [1,x_1,x_2,x_1^2,x_1x_2,x_2^2] [1,x1,x2,x12,x1x2,x22],然后利用映射后的坐标来计算 w [ 1 , x 1 , x 2 , x 1 2 , x 1 x 2 , x 2 2 ] T + b w[1,x_1,x_2,x_1^2,x_1x_2,x_2^2]^T+b w[1,x1,x2,x12,x1x2,x22]T+b来作为判别函数,那么这个分界面问题的对偶函数中 ϕ ( x i ) ϕ ( x j ) \phi(x_i)\phi(x_j) ϕ(xi)ϕ(xj)就是上面的 ( x ⋅ z + 1 ) p (x\cdot z+1)^p (x⋅z+1)p的形式,也就是我们不用知道中间映射后的坐标,而可以直接计算 ( x i ⋅ x j + 1 ) p (x_i\cdot x_j+1)^p (xi⋅xj+1)p。
高斯核函数; K ( x , z ) = exp ( − ∥ x − z ∥ 2 2 σ 2 ) K(x,z)=\exp(-\frac{{\|x-z\|}^2}{2\sigma^2}) K(x,z)=exp(−2σ2∥x−z∥2),计算难度大大减小,但是这个核函数对应的映射函数不容易求出来。
K ( x , z ) = exp ( − ( x 1 − z 1 ) 2 + ( x 2 − z 2 ) 2 2 σ 2 ) = exp ( − x 1 2 + z 1 2 − 2 x 1 z 1 + x 2 2 + z 2 2 − 2 x 2 z 2 2 σ 2 ) = exp ( − x 1 2 2 σ 2 ) exp ( − z 1 2 2 σ 2 ) exp ( − x 2 2 2 σ 2 ) exp ( − z 2 2 2 σ 2 ) exp ( 2 x 1 z 1 2 σ 2 ) exp ( 2 x 2 z 2 2 σ 2 ) = exp ( − x 1 2 2 σ 2 ) exp ( − z 1 2 2 σ 2 ) exp ( − x 2 2 2 σ 2 ) exp ( − z 2 2 2 σ 2 ) [ 1 + 2 x 1 z 1 2 σ 2 + ⋯ + 1 n ! ( 2 x 1 z 1 2 σ 2 ) n + ⋯ ] [ 1 + 2 x 2 z 2 2 σ 2 + ⋯ + 1 n ! ( 2 x 2 z 2 2 σ 2 ) n + ⋯ ] = exp ( − x 1 2 2 σ 2 ) exp ( − z 1 2 2 σ 2 ) exp ( − x 2 2 2 σ 2 ) exp ( − z 2 2 2 σ 2 ) [ ∑ t = 0 + ∞ ∑ k = 0 + ∞ 1 t ! ( 2 x 1 z 1 2 σ 2 ) t 1 k ! ( 2 x 2 z 2 2 σ 2 ) k ] = exp ( − x 1 2 2 σ 2 ) exp ( − x 2 2 2 σ 2 ) [ 1 , x 1 σ , ⋯ , 1 n ! ( x 1 σ ) n , ⋯ , x 2 σ , x 1 x 2 σ 2 , ⋯ , 1 n ! ( x 1 n x 2 σ n + 1 ) , ⋯ , 1 t ! n ! x 1 t x 2 n σ t + n , ⋯ ] ∗ exp ( − z 1 2 2 σ 2 ) exp ( − z 2 2 2 σ 2 ) [ 1 , z 1 σ , ⋯ , 1 n ! ( z 1 σ ) n , ⋯ , z 2 σ , z 1 z 2 σ 2 , ⋯ , 1 n ! ( z 1 n z 2 σ n + 1 ) , ⋯ , 1 t ! n ! z 1 t z 2 n σ t + n , ⋯ ] \begin{align*} K(x,z)=&\exp(-\frac{(x_1-z_1)^2+(x_2-z_2)^2}{2\sigma^2})\\ =&\exp(-\frac{x_1^2+z_1^2-2x_1z_1+x_2^2+z_2^2-2x_2z_2}{2\sigma^2})\\ =&\exp(-\frac{x_1^2}{2\sigma^2})\exp(-\frac{z_1^2}{2\sigma^2})\exp(-\frac{x_2^2}{2\sigma^2})\exp(-\frac{z_2^2}{2\sigma^2})\exp(\frac{2x_1z_1}{2\sigma^2})\exp(\frac{2x_2z_2}{2\sigma^2})\\ =&\exp(-\frac{x_1^2}{2\sigma^2})\exp(-\frac{z_1^2}{2\sigma^2})\exp(-\frac{x_2^2}{2\sigma^2})\exp(-\frac{z_2^2}{2\sigma^2})[1+\frac{2x_1z_1}{2\sigma^2}+\cdots+\frac{1}{n!}(\frac{2x_1z_1}{2\sigma^2})^n+\cdots][1+\frac{2x_2z_2}{2\sigma^2}+\cdots+\frac{1}{n!}(\frac{2x_2z_2}{2\sigma^2})^n+\cdots]\\ =&\exp(-\frac{x_1^2}{2\sigma^2})\exp(-\frac{z_1^2}{2\sigma^2})\exp(-\frac{x_2^2}{2\sigma^2})\exp(-\frac{z_2^2}{2\sigma^2})[\sum_{t=0}^{+\infty}\sum_{k=0}^{+\infty}\frac{1}{t!}(\frac{2x_1z_1}{2\sigma^2})^t\frac{1}{k!}(\frac{2x_2z_2}{2\sigma^2})^k]\\ =&\exp(-\frac{x_1^2}{2\sigma^2})\exp(-\frac{x_2^2}{2\sigma^2})[1,\frac{x_1}{\sigma},\cdots,\sqrt{\frac{1}{n!}}(\frac{x_1}{\sigma})^n,\cdots,\frac{x_2}{\sigma},\frac{x_1x_2}{\sigma^2},\cdots,\sqrt{\frac{1}{n!}}(\frac{x_1^nx_2}{\sigma^{n+1}}),\cdots,\sqrt{\frac{1}{t!n!}}\frac{x_1^tx_2^n}{\sigma^{t+n}},\cdots]*\\ &\exp(-\frac{z_1^2}{2\sigma^2})\exp(-\frac{z_2^2}{2\sigma^2})[1,\frac{z_1}{\sigma},\cdots,\sqrt{\frac{1}{n!}}(\frac{z_1}{\sigma})^n,\cdots,\frac{z_2}{\sigma},\frac{z_1z_2}{\sigma^2},\cdots,\sqrt{\frac{1}{n!}}(\frac{z_1^nz_2}{\sigma^{n+1}}),\cdots,\sqrt{\frac{1}{t!n!}}\frac{z_1^tz_2^n}{\sigma^{t+n}},\cdots] \end{align*} K(x,z)======exp(−2σ2(x1−z1)2+(x2−z2)2)exp(−2σ2x12+z12−2x1z1+x22+z22−2x2z2)exp(−2σ2x12)exp(−2σ2z12)exp(−2σ2x22)exp(−2σ2z22)exp(2σ22x1z1)exp(2σ22x2z2)exp(−2σ2x12)exp(−2σ2z12)exp(−2σ2x22)exp(−2σ2z22)[1+2σ22x1z1+⋯+n!1(2σ22x1z1)n+⋯][1+2σ22x2z2+⋯+n!1(2σ22x2z2)n+⋯]exp(−2σ2x12)exp(−2σ2z12)exp(−2σ2x22)exp(−2σ2z22)[t=0∑+∞k=0∑+∞t!1(2σ22x1z1)tk!1(2σ22x2z2)k]exp(−2σ2x12)exp(−2σ2x22)[1,σx1,⋯,n!1(σx1)n,⋯,σx2,σ2x1x2,⋯,n!1(σn+1x1nx2),⋯,t!n!1σt+nx1tx2n,⋯]∗exp(−2σ2z12)exp(−2σ2z22)[1,σz1,⋯,n!1(σz1)n,⋯,σz2,σ2z1z2,⋯,n!1(σn+1z1nz2),⋯,t!n!1σt+nz1tz2n,⋯]
所以两个映射函数分别如上所示:
ϕ ( x ) = exp ( − x 1 2 2 σ 2 ) exp ( − x 2 2 2 σ 2 ) [ 1 , x 1 σ , ⋯ , 1 n ! ( x 1 σ ) n , ⋯ , x 2 σ , x 1 x 2 σ 2 , ⋯ , 1 n ! ( x 1 n x 2 σ n + 1 ) , ⋯ , 1 t ! n ! x 1 t x 2 n σ t + n , ⋯ ] \phi(x)=\exp(-\frac{x_1^2}{2\sigma^2})\exp(-\frac{x_2^2}{2\sigma^2})[1,\frac{x_1}{\sigma},\cdots,\sqrt{\frac{1}{n!}}(\frac{x_1}{\sigma})^n,\cdots,\frac{x_2}{\sigma},\frac{x_1x_2}{\sigma^2},\cdots,\sqrt{\frac{1}{n!}}(\frac{x_1^nx_2}{\sigma^{n+1}}),\cdots,\sqrt{\frac{1}{t!n!}}\frac{x_1^tx_2^n}{\sigma^{t+n}},\cdots] ϕ(x)=exp(−2σ2x12)exp(−2σ2x22)[1,σx1,⋯,n!1(σx1)n,⋯,σx2,σ2x1x2,⋯,n!1(σn+1x1nx2),⋯,t!n!1σt+nx1tx2n,⋯]
如果只看后面的向量的话,他就是泰勒展开式中各个项,但是它前面还乘上了系数 exp ( − x 1 2 2 σ 2 ) exp ( − x 2 2 2 σ 2 ) \exp(-\frac{x_1^2}{2\sigma^2})\exp(-\frac{x_2^2}{2\sigma^2}) exp(−2σ2x12)exp(−2σ2x22)缩放了一下。
换句话说,这个映射函数把原始特征映射为了一个无穷维的坐标,我们实际上做的是用这个映射后的坐标 exp ( − x 1 2 2 σ 2 ) exp ( − x 2 2 2 σ 2 ) [ 1 , x 1 σ , ⋯ , 1 n ! ( x 1 σ ) n , ⋯ , x 2 σ , x 1 x 2 σ 2 , ⋯ , 1 n ! ( x 1 n x 2 σ n + 1 ) , ⋯ , 1 t ! n ! x 1 t x 2 n σ t + n , ⋯ ] \exp(-\frac{x_1^2}{2\sigma^2})\exp(-\frac{x_2^2}{2\sigma^2})[1,\frac{x_1}{\sigma},\cdots,\sqrt{\frac{1}{n!}}(\frac{x_1}{\sigma})^n,\cdots,\frac{x_2}{\sigma},\frac{x_1x_2}{\sigma^2},\cdots,\sqrt{\frac{1}{n!}}(\frac{x_1^nx_2}{\sigma^{n+1}}),\cdots,\sqrt{\frac{1}{t!n!}}\frac{x_1^tx_2^n}{\sigma^{t+n}},\cdots] exp(−2σ2x12)exp(−2σ2x22)[1,σx1,⋯,n!1(σx1)n,⋯,σx2,σ2x1x2,⋯,n!1(σn+1x1nx2),⋯,t!n!1σt+nx1tx2n,⋯]去构成分界面 w exp ( − x 1 2 2 σ 2 ) exp ( − x 2 2 2 σ 2 ) [ 1 , x 1 σ , ⋯ , 1 n ! ( x 1 σ ) n , ⋯ , x 2 σ , x 1 x 2 σ 2 , ⋯ , 1 n ! ( x 1 n x 2 σ n + 1 ) , ⋯ , 1 t ! n ! x 1 t x 2 n σ t + n , ⋯ ] + b w\exp(-\frac{x_1^2}{2\sigma^2})\exp(-\frac{x_2^2}{2\sigma^2})[1,\frac{x_1}{\sigma},\cdots,\sqrt{\frac{1}{n!}}(\frac{x_1}{\sigma})^n,\cdots,\frac{x_2}{\sigma},\frac{x_1x_2}{\sigma^2},\cdots,\sqrt{\frac{1}{n!}}(\frac{x_1^nx_2}{\sigma^{n+1}}),\cdots,\sqrt{\frac{1}{t!n!}}\frac{x_1^tx_2^n}{\sigma^{t+n}},\cdots]+b wexp(−2σ2x12)exp(−2σ2x22)[1,σx1,⋯,n!1(σx1)n,⋯,σx2,σ2x1x2,⋯,n!1(σn+1x1nx2),⋯,t!n!1σt+nx1tx2n,⋯]+b作为分界面,其中 w w w为无穷维向量,那么这个分界面问题的对偶函数中 ϕ ( x i ) ϕ ( x j ) \phi(x_i)\phi(x_j) ϕ(xi)ϕ(xj)就是上面的 exp ( − ( x 1 − z 1 ) 2 + ( x 2 − z 2 ) 2 2 σ 2 ) \exp(-\frac{(x_1-z_1)^2+(x_2-z_2)^2}{2\sigma^2}) exp(−2σ2(x1−z1)2+(x2−z2)2)的形式,也就是我们不用知道中间映射后的坐标,而可以直接计算 exp ( − ( x 1 − z 1 ) 2 + ( x 2 − z 2 ) 2 2 σ 2 ) \exp(-\frac{(x_1-z_1)^2+(x_2-z_2)^2}{2\sigma^2}) exp(−2σ2(x1−z1)2+(x2−z2)2)。
相关文章:
)
支持向量机(二)
文章目录 前言具体内容 前言 总算要对稍微有点难度的地方动手了,前面介绍的线性可分或者线性不可分的情况,都是使用平面作为分割面的,现在我们采用另一种分割面的设计方法,也就是核方法。 核方法涉及的分割面不再是 w x b 0 wx…...
Arrays.asList 和 null 类型
一、Arrays.asList 类型简析 Arrays.asList() 返回的List 是它的内部类,不能使用 retainAll() 取交集,导致元素的删除,会报错。 List<String> list Arrays.asList(value.split(",")); 替换为> List<String> list…...

《论文阅读》用提示和释义模拟对话情绪识别的思维过程 IJCAI 2023
《论文阅读》用提示和复述模拟对话情绪识别的思维过程 IJCAI 2023 前言简介相关知识prompt engineeringparaphrasing模型架构第一阶段第二阶段History-oriented promptExperience-oriented Prompt ConstructionLabel Paraphrasing损失函数前言 你是否也对于理解论文存在困惑?…...
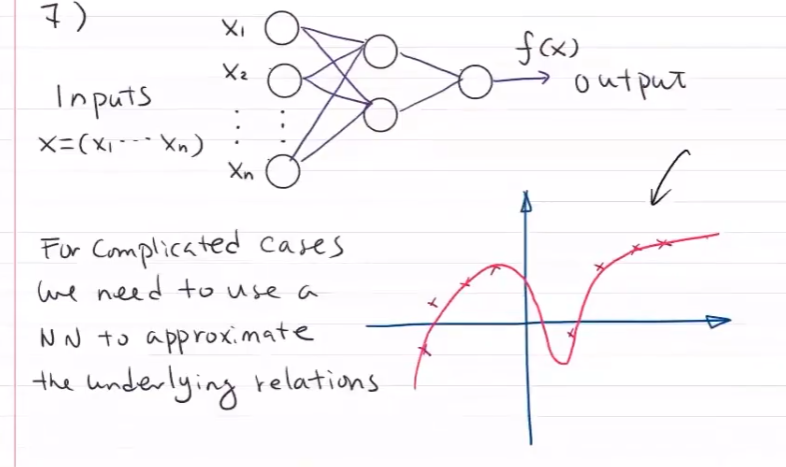
【AI】机器学习——绪论
文章目录 1.1 机器学习概念1.1.1 定义统计机器学习与数据挖掘区别机器学习前提 1.1.2 术语1.1.3 特点以数据为研究对象目标方法——基于数据构建模型SML三要素SML步骤 1.2 分类1.2.1 参数化/非参数化方法1.2.2 按算法分类1.2.3 按模型分类概率模型非概率模型逻辑斯蒂回归 1.2.4…...

linux 查看端口占用
查看端口占用 使用lsof 可以使用lsof -i:端口号 来查看端口占用情况 lsof -i:8010COMMAND PID USER FD TYPE DEVICE SIZE/OFF NODE NAMEnginx 35653 zhanghe 10u IPv4 0xcac2e413ddf9c5b9 0t0 TCP *:8010 (LISTEN)nginx 35654 zhanghe 10u…...

modernC++手撸任意层神经网络22前向传播反向传播梯度下降等23代码补全的例子0901b
以下神经网络代码,请添加输入:{{1,0},{1,1}},输出{1,0};添加反向传播,梯度下降等训练! 以下神经网络代码,请添加输入:{{1,0},{1,1}},输出{1,0};添加反向传播,梯度下降等训练! #include <iostream> #include<vector> #include<Eigen/Dense> #include<rando…...
tkinter控件样式
文章目录 以按钮为例共有参数动态属性 tkinter系列: GUI初步💎布局💎绑定变量💎绑定事件💎消息框💎文件对话框💎控件样式扫雷小游戏💎强行表白神器 以按钮为例 tkinter对控件的诸…...

【linux命令讲解大全】042. 深入了解 which 命令:查找和显示命令的绝对路径
文章目录 which补充说明语法选项参数实例 从零学 python which 查找并显示给定命令的绝对路径 补充说明 which 命令用于查找并显示给定命令的绝对路径,环境变量 PATH 中保存了查找命令时需要遍历的目录。which 指令会在环境变量 $PATH 设置的目录里查找符合条件的…...
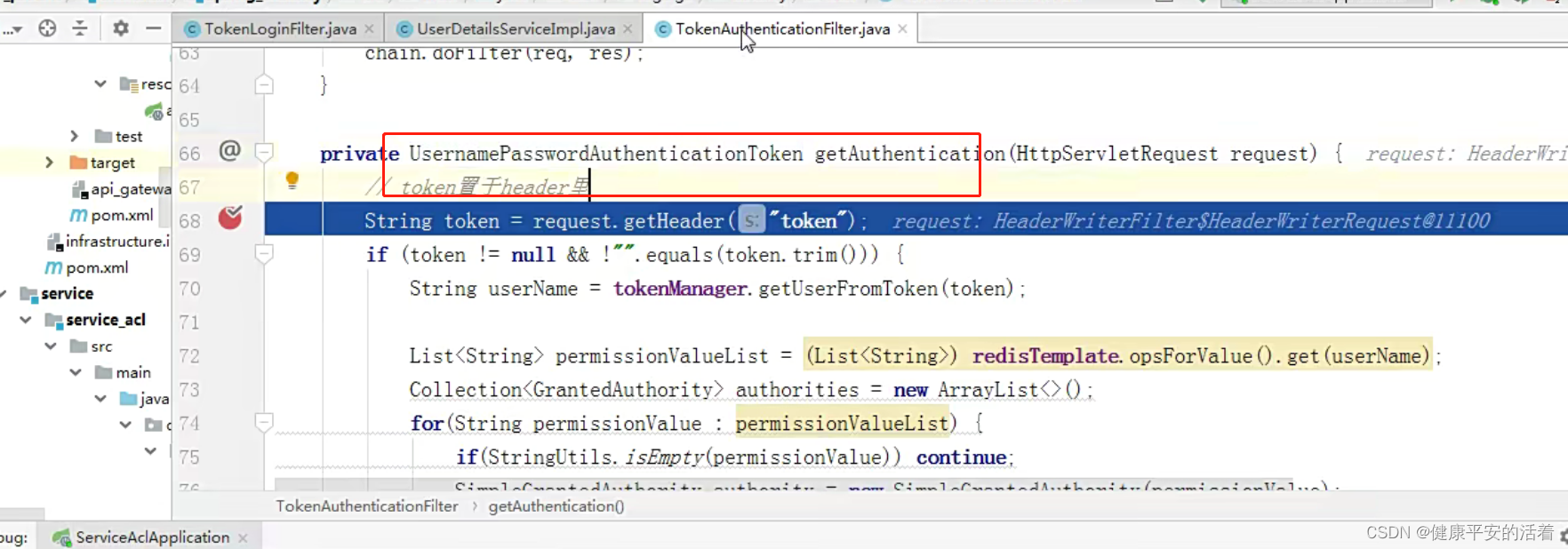
实战项目 在线学院之集成springsecurity的配置以及执行流程
一 后端操作配置 1.0 工程结构 1.1 在common下创建spring_security模块 1.2 pom文件中依赖的注入 1.3 在service_acl模块服务中引入spring-security权限认证模块 1.3.1 service_acl引入spring-security 1.3.2 在service_acl编写查询数据库信息 定义userDetailServiceImpl 查…...
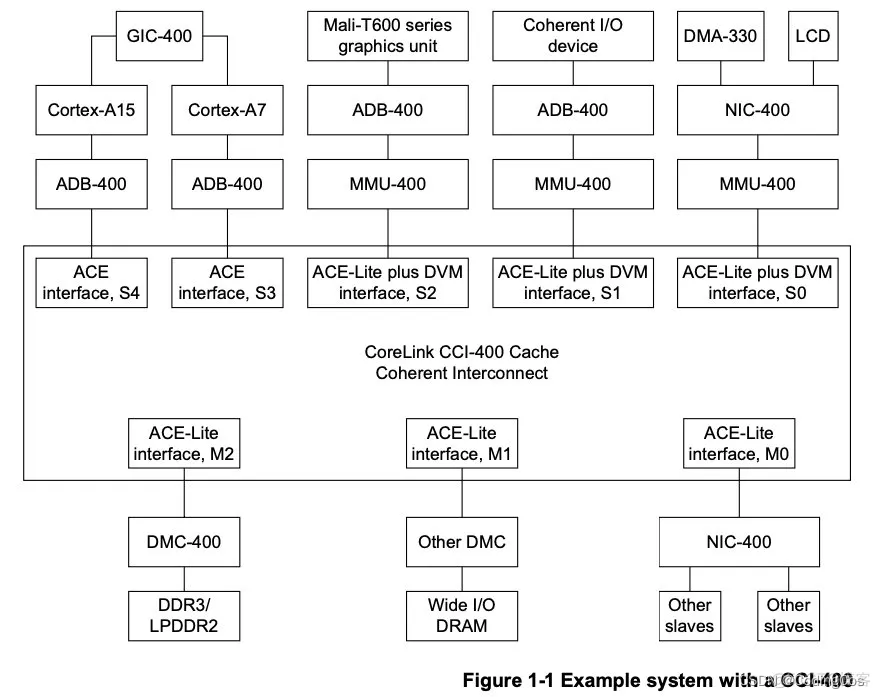
【ARM CoreLink CCI-400 控制器简介】
文章目录 CCI-400 介绍 CCI-400 介绍 CCI(Cache Coherent Interconnect)是ARM 中 的Cache一致性控制器。 CCI-400 将 Interconnect 和coherency 功能结合到一个模块中。它支持多达两个ACE master 点的interface,例如: Cortex-A…...
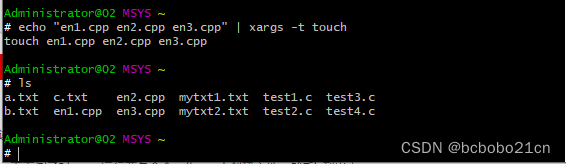
Linux xargs命令继续学习
之前学习过Linux xargs,对此非常的不熟悉,下面继续学习一下; xargs 可以将管道或标准输入(stdin)数据转换成命令行参数,也能够从文件的输出中读取数据; xargs也可以给命令传递参数;…...

【广州华锐互动】数字孪生智慧楼宇3D可视化系统:掌握实时运行状态,优化运营管理
在过去的几年中,科技的发展极大地改变了我们的生活和工作方式。其中,三维数据可视化技术的出现,为我们提供了全新的理解和观察世界的方式。特别是在建筑行业,数字孪生智慧楼宇3D可视化系统的出现,让我们有机会重新定义…...

20230904工作心得:集合应该如何优雅判空?
1 集合判空 List<String> newlist null;//空指针if( !newlist.isEmpty()){newlist.forEach(System.out::println);}//空指针if(newlist.size()>0 && newlist!null){newlist.forEach(System.out::println);}//可行if(newlist!null && newlist.size()&…...

使用Python进行健身手表数据分析
健身手表(Fitness Watch)数据分析涉及分析健身可穿戴设备或智能手表收集的数据,以深入了解用户的健康和活动模式。这些设备可以跟踪所走的步数、消耗的能量、步行速度等指标。本文将带您完成使用Python进行Fitness Watch数据分析的任务。 Fitness Watch数据分析是健…...
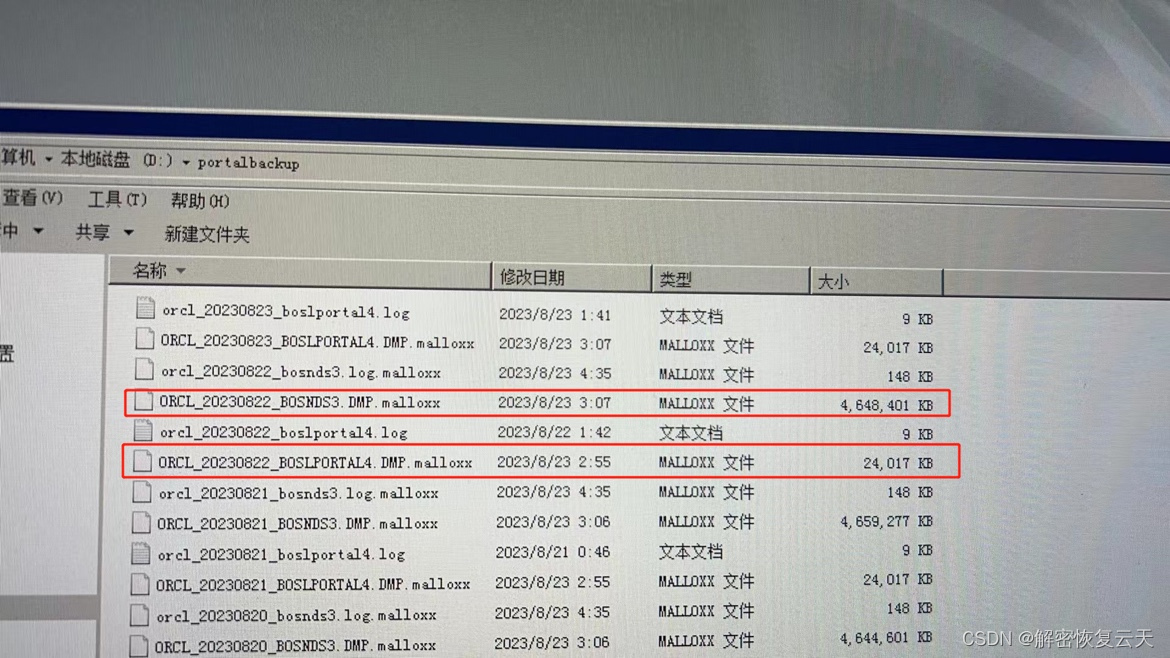
什么是malloxx勒索病毒,服务器中malloxx勒索病毒了怎么办?
Malloxx勒索病毒是一种新型的电脑病毒,它通过加密用户电脑中的重要文件数据来威胁用户,并以此勒索钱财。这种病毒并不是让用户的电脑瘫痪,而是以非常独特的方式进行攻击。在感染了Malloxx勒索病毒后,它会加密用户服务器中的数据&a…...
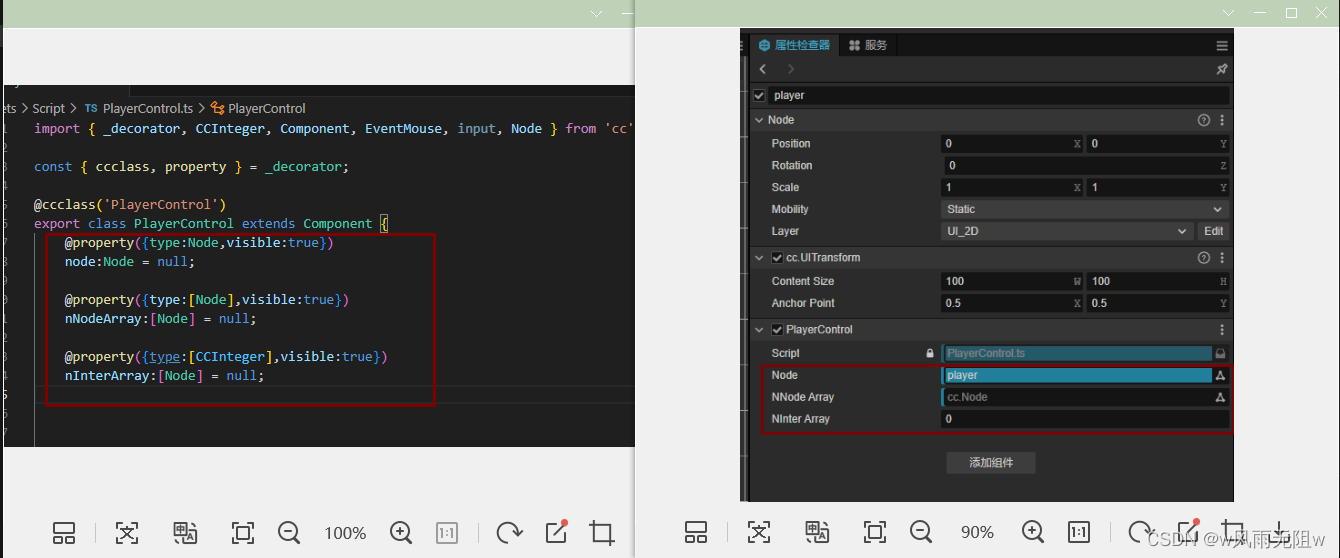
CocosCreator3.8研究笔记(六)CocosCreator 脚本装饰器的理解
一、什么是装饰器? 装饰器是TypeScript脚本语言中的概念。 TypeScript的解释:在一些场景下,我们需要额外的特性来支持标注或修改类及其成员。装饰器(Decorators)为我们在类的声明及成员上通过元编程语法添加标注提供了…...

docker login harbor http login登录
前言 搭建的 harbor 仓库为 http 协议,在本地登录时出现如下报错: docker login http://192.168.xx.xx Username: admin Password: Error response from daemon: Get "https://192.168.xx.xx/v2/": dialing 192.168.xx.xx:443 matches static …...
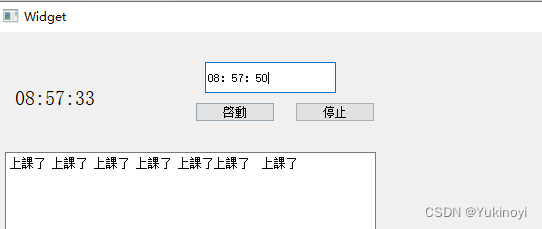
day5 qt
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this);timer_idthis->startTimer(100);//啓動一個定時器 每100ms發送一次信號ui->Edit1->setPlaceholderTex…...
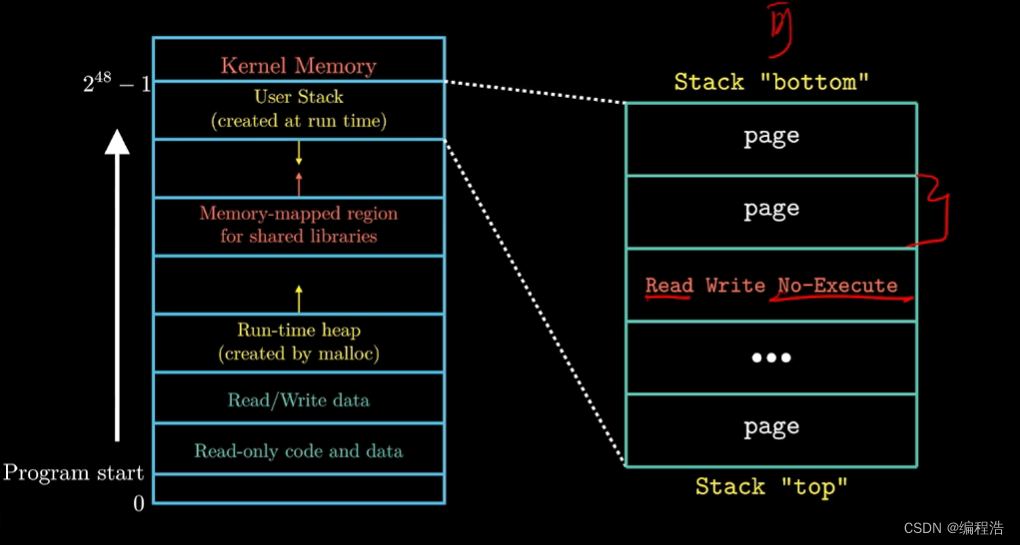
【80天学习完《深入理解计算机系统》】第十三天 3.7 缓冲区溢出 attack lab
3.7 缓冲区溢出 && attack lab...

Hadoop生态之hive
一 概述与特点 之所以把Hive放在Hadoop生态里面去写,是因为它本身依赖Hadoop。Hive是基于Hadoop的一个数据仓库工具,可以将结构化的数据文件映射为一张数据库表,并提供类 SQL 查询功能。 其本质是将 SQL 转换为 MapReduce/Spark 的任务进行运算,底层由 HDFS 来提供…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

redis和redission的区别
Redis 和 Redisson 是两个密切相关但又本质不同的技术,它们扮演着完全不同的角色: Redis: 内存数据库/数据结构存储 本质: 它是一个开源的、高性能的、基于内存的 键值存储数据库。它也可以将数据持久化到磁盘。 核心功能: 提供丰…...
