数据结构和算法(1):开始
算法概述
所谓算法,即特定计算模型下,旨在解决特定问题的指令序列
输入 待处理的信息(问题)
输出 经处理的信息(答案)
正确性 的确可以解决指定的问题
确定性 任一算法都可以描述为一个由基本操作组成的序列
可行性 每一基本操作都可实现,且在常数时间内完成
有穷性 对于任何输入,经有穷次基本操作,都可以得到输出
…
程序未必是算法,例如发生死循环或者栈溢出时。
算法在满足基本要求时,最重要的是:速度尽可能快,存储空间尽可能少(效率)。
计算模型
两个主要方面:
1.正确性:算法功能与问题要求一致?
2.成本:运行时间 + 存储空间
计算成本: T ( n ) = max { T ( P ) ∣ ∣ P ∣ = n } T(n)=\max \{T(P) \space \boldsymbol | \space |P| = n \} T(n)=max{T(P) ∣ ∣P∣=n} 遵守最坏情况分析原则。
特定问题,不同算法下,需要抽象出一种理想的平台或模型,不再依赖于种种具体因素,从而直接准确地描述、测量并评价算法。
渐进复杂度
随着问题规模地增长,运算成本增大
T ( n ) = O ( f ( n ) ) if ∃ c > 0 , n ≫ 2 , T ( n ) < c ⋅ f ( n ) T(n) = \mathcal O(f(n)) \space \text{if } \exists \space c>0,n\gg 2, T(n)<c\cdot f(n) T(n)=O(f(n)) if ∃ c>0,n≫2,T(n)<c⋅f(n)
与 T ( n ) T(n) T(n) 相比, f ( n ) f(n) f(n)更为简洁,但依然反应前者地增长趋势:
常系数可忽略: O ( f ( n ) ) = ( c × f ( n ) ) \mathcal O(f(n)) = (c \times f(n)) O(f(n))=(c×f(n))
低次项可忽略: O ( n a + n b ) = O ( n a ) , a > b > 0 \mathcal O(n^a+n^b)=\mathcal O(n^a),a>b>0 O(na+nb)=O(na),a>b>0

1.常数复杂度为: O ( 1 ) \mathcal O(1) O(1)
算法不含转向(循环、调用、递归等),必顺序执行即复杂度为 O ( 1 ) \mathcal O(1) O(1)
2.对数复杂度为: O ( log n ) \mathcal O(\log n) O(logn)
∀ c > 0 , l o g ( n ) = O ( n c ) \forall c>0,log(n)=\mathcal O(n^c) ∀c>0,log(n)=O(nc),因此对数复杂度无限接近于常数
3.多项式复杂度: O ( n c ) \mathcal O(n^c) O(nc)
4.指数复杂度: O ( a n ) \mathcal O(a^n) O(an)
计算成本增长极快,通常认为不可以接受
复杂度增长速度
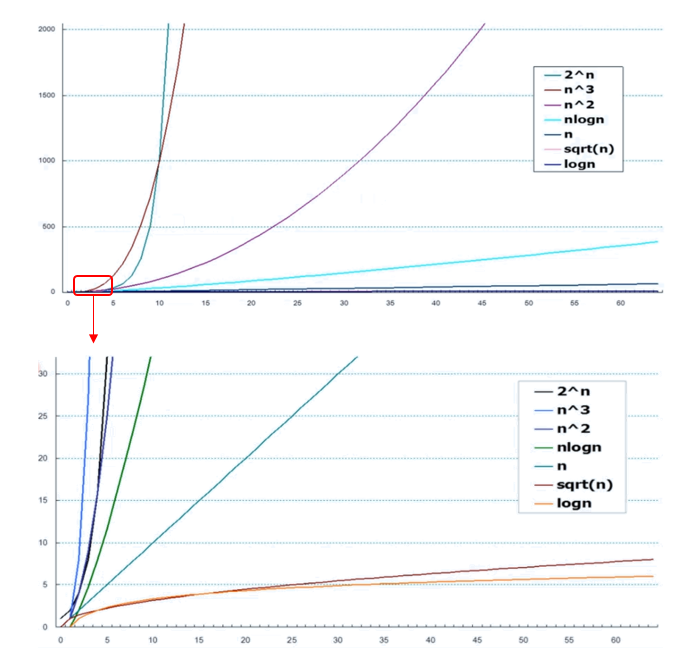
复杂度分析
算法分析的两个主要任务 = 正确性(不变性×单调性) + 复杂度
C++ 等高级语言的基本指令,均等效于常数条 RAM 的基本指令;在渐进意义下,两者相当。
复杂度分析的主要方法:
1.迭代:级数求和;
2.递归:递归追踪 + 递推方程;
实例:冒泡排序
问题:给定 n 个整数,将它们按(非降)序排列
观察:有序/无序序列中,任意/总有一对相邻元素顺序/逆序
思路:(扫描交换)依次比较每一个相邻元素,如果必要,交换之,若整躺扫描都没有进行交换,则排序完成;否则,再做一趟扫描交换。
void bubblesort(int A[],int n){for(bool sorted = false; sorted = !sorted; n--){ // 逐躺扫描交换,直至完全有序for(int i = 1; i< n; i++){ // 自左向右,逐对检查A[0,n)内各相邻元素if(A[i-1]>A[i]){ // 若逆序,则swap(A[i-1], A[i]); //令其互换,同时sorted = false; //清楚(全局)有序标志 }}}
}
不变性:经过 k 轮扫描交换后,最大的 k 个元素必然就位;
单调性:经过 k 轮扫描交换后,问题规模缩减至 n-k;
正确性:经过最多 n 躺扫描后,算法必然终止,且能正确解答。
迭代与递归
递归跟踪分析:检查每个递归实例,累计所需时间(调用语句本身,计入对应的子实例),其总和即算法执行时间。
实例:数组求和(二分递归)
int sum(int A[], int lo, int hi){ //区间范围A[lo, hi]if(lo == hi) return A[lo]; //base caseint mi = (lo + hi) >> 1; //右移一位,相当于除以2 只有正数适用,而负数不适用return sum(A, lo, mi) + sum(A, mi+1, hi);
} //入口形式为 sum(A,0,n-1)
master theorem

动态规划
实例:Fibonacci 序列
F ( 1 ) = 1 , F ( 2 ) = 1 , F ( n ) = F ( n − 1 ) + F ( n − 2 ) ( n > = 3 , n ∈ N ∗ ) F(1)=1,F(2)=1, F(n)=F(n-1)+F(n-2)(n>=3,n∈N*) F(1)=1,F(2)=1,F(n)=F(n−1)+F(n−2)(n>=3,n∈N∗)
计算Fibonacci数列的第n项(迭代版):O(n)
__int64 fibI ( int n ) { __int64 f = 1, g = 0; //初始化:fib(-1)、fib(0)while ( 0 < n-- ) { g += f; f = g - f; } //依据原始定义,通过n次加法和减法计算fib(n)return g; //返回
}
计算Fibonacci数列的第n项(二分递归版):O(2^n)
__int64 fib ( int n ) { return ( 2 > n ) ?( __int64 ) n //若到达递归基,直接取值: fib ( n - 1 ) + fib ( n - 2 ); //否则,递归计算前两项,其和即为正解
}
计算Fibonacci数列第n项(线性递归版):O(n)
__int64 fib ( int n, __int64& prev ) { //入口形式fib(n, prev)if ( 0 == n ) //若到达递归基,则{ prev = 1; return 0; } //直接取值:fib(-1) = 1, fib(0) = 0else { //否则__int64 prevPrev; prev = fib ( n - 1, prevPrev ); //递归计算前两项return prevPrev + prev; //其和即为正解}
} //用辅助变量记录前一项,返回数列的当前项,O(n)
//Fib.h
using Rank = unsigned int;class Fib { //Fibonacci数列类
private:Rank f, g; //f = fib(k - 1), g = fib(k)。均为int型,很快就会数值溢出
public:Fib ( Rank n ) //初始化为不小于n的最小Fibonacci项{ f = 1; g = 0; while ( g < n ) next(); } //fib(-1), fib(0),O(log_phi(n))时间Rank get() { return g; } //获取当前Fibonacci项,O(1)时间Rank next() { g += f; f = g - f; return g; } //转至下一Fibonacci项,O(1)时间Rank prev() { f = g - f; g -= f; return g; } //转至上一Fibonacci项,O(1)时间
};//main.c
#include<ctime>
#include<iostream>
using namespace std;#include "Fib.h"__int64 fibI ( int n ); //迭代版
__int64 fib ( int n ); //二分递归版
__int64 fib ( int n, __int64& f ); //线性递归版int main ( int argc, char* argv[] ) { //测试FIB
// 检查参数if ( 2 > argc ) { fprintf ( stderr, "Usage: %s <Rank>\n", argv[0] ); return 1; }int n = atoi ( argv[1] );
// 依次计算Fibonacci数列各项printf ( "\n------------- class Fib -------------\n" );Fib f ( 0 );for ( int i = 0; i < n; i++, f.next() )printf ( "fib(%2d) = %d\n", i, f.get() );for ( int i = 0; i <= n; i++, f.prev() )printf ( "fib(%2d) = %d\n", n - i, f.get() );printf ( "\n------------- Iteration -------------\n" );for ( int i = 0; i < n; i++ )printf ( "fib(%2d) = %22I64d\n", i, fibI ( i ) );printf ( "\n------------- Linear Recursion -------------\n" );for ( int i = 0; i < n; i++ ) {__int64 f;printf ( "fib(%2d) = %22I64d\n", i, fib ( i, f ) );}printf ( "\n------------- Binary Recursion -------------\n" );for ( int i = 0; i < n; i++ )printf ( "fib(%2d) = %22I64d\n", i, fib ( i ) );return 0;
}
实例:LCS:最长公共子序列
两个字符串中找到最长的子序列,这里明确两个含义:
1.子串:表示连续的一串字符 。
2.子序列:表示不连续的一串字符。
1.两个字符串具有相同尾序,那么同时去掉两者的尾序,不影响它们的距离
2.如果 A 和 B 是不同的符号 ( A ≠ B A≠B A=B),则 L C S ( X A , Y B ) LCS(X^A,Y^B) LCS(XA,YB) 是以下两者的最大者: L C S ( X A , Y ) , L C S ( X , Y B ) LCS(X^A,Y), LCS(X,Y ^B) LCS(XA,Y),LCS(X,YB) ,适用于所有字符串 X 、 Y X、Y X、Y
给定两个字符串S1和S2,我们需要找到一个最长的子序列,该子序列同时出现在S1和S2中。这个子序列不要求在原字符串中是连续的,但在原字符串中的相对顺序必须与原字符串中的顺序相同。
举例说明:
假设有两个字符串:
S1 = “ABCBDAB”
S2 = “BDCAB”
它们的一个最长公共子序列是"BCAB",它在两个字符串中都出现,而且是最长的。
LCS问题的目标是找到这个最长的公共子序列的长度以及可能的子序列之一。在动态规划中,可以使用一个二维表格来解决这个问题,表格中的值表示两个字符串在不同位置的字符之间的LCS长度。
通过解决LCS问题,我们可以解决许多实际应用,如文本比对、版本控制、DNA序列比对等。这个问题在算法设计和字符串处理中具有重要性。
#include <iostream>
#include <vector>
#include <string>using namespace std;string longestCommonSubsequence(string s1, string s2) {int m = s1.length();int n = s2.length();// 创建DP表,初始化为0vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));// 填充DP表for (int i = 1; i <= m; ++i) {for (int j = 1; j <= n; ++j) {if (s1[i - 1] == s2[j - 1]) {dp[i][j] = dp[i - 1][j - 1] + 1;} else {dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);}}}// 回溯构建最长公共子序列string lcs = "";int i = m, j = n;while (i > 0 && j > 0) {if (s1[i - 1] == s2[j - 1]) {lcs = s1[i - 1] + lcs;i--;j--;} else if (dp[i - 1][j] > dp[i][j - 1]) {i--;} else {j--;}}return lcs;
}int main() {string s1 = "ABCBDAB";string s2 = "BDCAB";string result = longestCommonSubsequence(s1, s2);cout << "Longest Common Subsequence: " << result << endl;return 0;
}
相关文章:

数据结构和算法(1):开始
算法概述 所谓算法,即特定计算模型下,旨在解决特定问题的指令序列 输入 待处理的信息(问题) 输出 经处理的信息(答案) 正确性 的确可以解决指定的问题 确定性 任一算法都可以描述为一个由基本操作组成的序…...

线下沙龙 | 从营销扩张到高效回款,游戏公司如何通过全链路运营实现高质量出海!
游戏出海,是近些年来中国产业的风暴出口,在2020至2023年期间保持着绝对的领航地位。公开数据显示,过去4年里,游戏在各类App出海份额中总体保持稳定,高达 64.9%。 但毕竟海外是陌生的市场,我们见过太多折戟沉…...
使用Jekyll + GitHub Pages搭建个人博客
本文将介绍如何使用Jekyll搭建个人博客,并部署在GitHub Pages上。 1.简介 Jekyll是一个强大的静态网站生成器,可以将Markdown、HTML、Liquid模板等文件转换为静态网站。Jekyll支持模板引擎、主题、插件、集成GitHub Pages等特性,可以帮助用…...
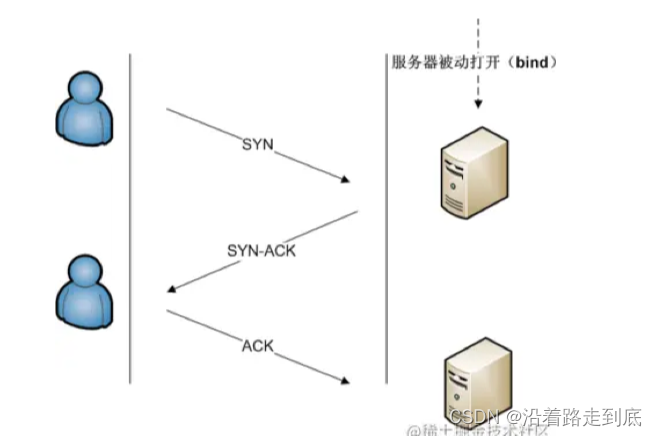
⽹络与HTTP 笔试题精讲1
OSI七层与TCP/IP 这个就是OSI参考模型,⽽实际我们现在的互联⽹世界是就是这个理论模型的落地叫做TCP/IP协议 TCP的三次握⼿与四次挥⼿ 客户端想要发送数据给服务端,在发送实际的数据之前,需要先在两端之间建⽴连接,数据发完以后也需要将该连接关闭。建⽴连接的过程就是我们…...
亲测有效:虚拟机安装gcc,报错Could not retrieve mirrorlist http://mirrorlist.centos.org
(网卡配置资料) 原因: 网络问题 报错详情: One of the configured repositories failed (未知),and yum doesnt have enough cached data to continue. At this point the onlysafe thing yum can do is fail. There are a few …...

机器人中的数值优化(十二)——带约束优化问题简介、LP线性规划
本系列文章主要是我在学习《数值优化》过程中的一些笔记和相关思考,主要的学习资料是深蓝学院的课程《机器人中的数值优化》和高立编著的《数值最优化方法》等,本系列文章篇数较多,不定期更新,上半部分介绍无约束优化,…...

如何解决使用 ISPC 构建编译项目代码的时候出现_ISPCAlloc、_ISPCLaunch、_ISPCSync的连接器错误
一般在编译 ISPC 代码到时候,构建方法如下: $ ispc add.ispc -o add.o -h add.h $ g main.cpp add.o 但是在一些情况下连接器会报以下错误: $ g main.cpp add.o Undefined symbols for architecture x86_64:"_ISPCAlloc", refer…...
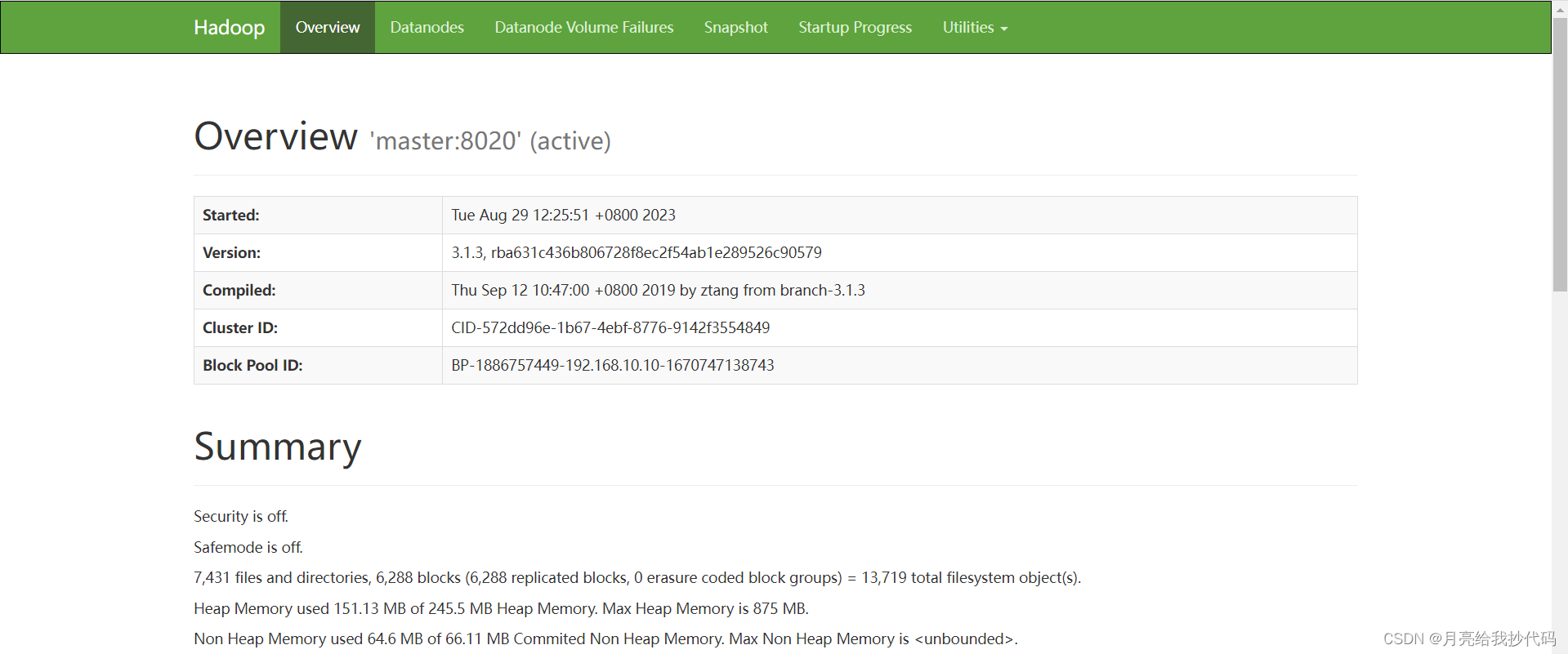
Hadoop 集群一直处于安全模式,强制退出后出现数据丢失警告。解决方法
文章目录 安全模式相关命令分析集群为什么一直处于安全模式解决方法 安全模式相关命令 # 查看安全模式状态 hdfs dfsadmin -safemode get# 进入安全模式 hdfs dfsadmin -safemode enter# 离开安全模式 hdfs dfsadmin -safemode leave# 强制退出安全模式 hdfs dfsadmin -safemo…...

四旋翼飞行器基本模型(MatlabSimulink)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
)
P1116 车厢重组(冒泡排序)
题目描述 在一个旧式的火车站旁边有一座桥,其桥面可以绕河中心的桥墩水平旋转。一个车站的职工发现桥的长度最多能容纳两节车厢,如果将桥旋转 180 180 180 度,则可以把相邻两节车厢的位置交换,用这种方法可以重新排列车厢的顺序…...
Android逆向学习(番外一)smali2java部分文件无法反编译的bug与修复方法
Android逆向学习(番外一)smali2java部分文件无法反编译的bug与修复方法 一、前言 昨天我和往常一样准备着android逆向(四)的博客,结果发现smali2java对某些文件无法进行逆向,我不知道windows会不会产生这…...
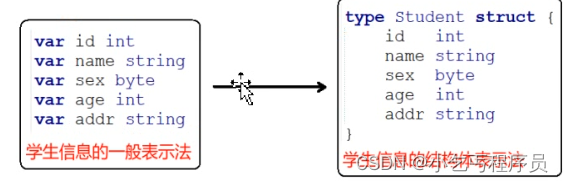
go语言基本操作---三
变量的内存和变量的地址 指针是一个代表着某个内存地址的值。这个内存地址往往是在内存中存储的另一个变量的值的起始位置。Go语言对指针的支持介于java语言和C/C语言之间,它即没有想Java语言那样取消了代码对指针的直接操作的能力,也避免了C/C语言中由…...

ArcGIS Enterprise + ArcGIS Pro 常用服务类型发布
发布前设置 门户连接 首先Pro需要先连接portal 添加portal门户地址,注意只到WA一级地址,并登录: 登录完成后,右键,设置为活动门户: 1. 发布动态地图服务 关联数据文件夹: 拖拽数据到地图…...

优思学院|亲和图案例:寻找六西格玛的项目
什么是亲和图? 亲和图(Affinity Diagram)主要功能在於分类归纳,协助在一堆杂乱无章的资料之中,有系统的归纳出几个大类,以利后续作业。通常先利用头脑风暴(Brainstorming)方式得到大…...

tomcat 的缓存机制
HTTP缓存:Tomcat支持HTTP缓存机制,可以通过设置响应头中的Cache-Control、Expires和ETag等字段来控制缓存策略。这些字段告诉浏览器是否可以缓存响应以及缓存的有效期等信息。 Servlet缓存:Tomcat还提供了Servlet缓存机制,它可以…...

laravel 压缩文件与解压文件
一、引入第三方类 composer require chumper/zipper二、第三方类配置 providers>[Chumper\Zipper\ZipperServiceProvider::class ]aliases > [Zipper > Chumper\Zipper\Zipper::class ]三、压缩解压缩实例 <?php namespace App\Http\Controllers\Upload; use A…...

kind搭建k8s集群用于测试
安装kind 需要先安装go kind基于go开发 #第一种安装方式#修改go源加快下载速度 go env -w GOPROXYhttps://goproxy.cn,direct #直接下载安装kind最新版本 go install sigs.k8s.io/kindlatest #进入GOPATH目录找到bin目录下kind执行程序 移动到环境变量里 mv ./kind /usr/local…...
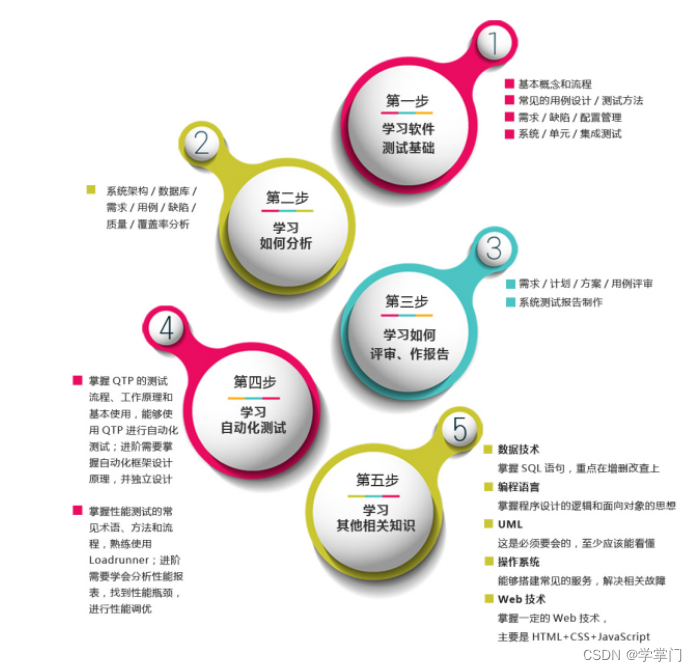
软件测试人需要掌握的测试知识架构体系(上)
软件计划与可行性研究(问题定义、可行性研究);需求分析;软件设计(概要设计、详细设计);编码;软件测试;运行与维护。 一、软件的生命周期(SDLC) 1、生存周期划分 各阶段…...

QT数据库,实现数据库增删改查
QT关于数据库的相关概念 QT将数据库分为三个层次: 数据库驱动层:QSqlDriver、QSqlDriverCreator、QSqlDriverCreatorBase、QSqlDriverPlugin sql接口层:QSqlDatabase、QSqlQuery、QSqlRecord、QSqlError 用户接口层:提供一些模…...

SQL-子查询
SQL 子查询 是指将一个SELECT查询(子查询)的结果用括号括起来作为另一个SQL语句的数据来源或者判断条件...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

云原生周刊:k0s 成为 CNCF 沙箱项目
开源项目推荐 HAMi HAMi(原名 k8s‑vGPU‑scheduler)是一款 CNCF Sandbox 级别的开源 K8s 中间件,通过虚拟化 GPU/NPU 等异构设备并支持内存、计算核心时间片隔离及共享调度,为容器提供统一接口,实现细粒度资源配额…...

Linux安全加固:从攻防视角构建系统免疫
Linux安全加固:从攻防视角构建系统免疫 构建坚不可摧的数字堡垒 引言:攻防对抗的新纪元 在日益复杂的网络威胁环境中,Linux系统安全已从被动防御转向主动免疫。2023年全球网络安全报告显示,高级持续性威胁(APT)攻击同比增长65%,平均入侵停留时间缩短至48小时。本章将从…...

门静脉高压——表现
一、门静脉高压表现 00:01 1. 门静脉构成 00:13 组成结构:由肠系膜上静脉和脾静脉汇合构成,是肝脏血液供应的主要来源。淤血后果:门静脉淤血会同时导致脾静脉和肠系膜上静脉淤血,引发后续系列症状。 2. 脾大和脾功能亢进 00:46 …...

Cursor AI 账号纯净度维护与高效注册指南
Cursor AI 账号纯净度维护与高效注册指南:解决限制问题的实战方案 风车无限免费邮箱系统网页端使用说明|快速获取邮箱|cursor|windsurf|augment 问题背景 在成功解决 Cursor 环境配置问题后,许多开发者仍面临账号纯净度不足导致的限制问题。无论使用 16…...

Spring是如何实现无代理对象的循环依赖
无代理对象的循环依赖 什么是循环依赖解决方案实现方式测试验证 引入代理对象的影响创建代理对象问题分析 源码见:mini-spring 什么是循环依赖 循环依赖是指在对象创建过程中,两个或多个对象相互依赖,导致创建过程陷入死循环。以下通过一个简…...

【Pandas】pandas DataFrame dropna
Pandas2.2 DataFrame Missing data handling 方法描述DataFrame.fillna([value, method, axis, …])用于填充 DataFrame 中的缺失值(NaN)DataFrame.backfill(*[, axis, inplace, …])用于**使用后向填充(即“下一个有效观测值”)…...
