【数据结构初阶】一. 复杂度讲解
=========================================================================
相关代码gitee自取:
C语言学习日记: 加油努力 (gitee.com)
=========================================================================
接上期:
学C的第三十四天【程序环境和预处理】_高高的胖子的博客-CSDN博客
=========================================================================
1 . 算法效率
(1). 什么是数据结构:
数据结构(Data Structure)是计算机存储、组织数据的方式,
指相互之间存在一种或多种特定关系的数据元素的集合。
(2). 什么是算法:
算法(Algorithm)就是定义良好的计算过程,
它取一个或一组的值为输入,并产生出一个或一组值作为输出。
简单来说算法就是一系列的计算步骤,用来将输入数据转化成输出结果。
(3). 算法的复杂度:
算法在编写成可执行程序后,运行时需要耗费时间资源和空间(内存)资源。
因此衡量一个算法的好坏,一般是从时间和空间两个维度来衡量的,
即时间复杂度和空间复杂度。
时间复杂度主要衡量一个算法的运行快慢,
而空间复杂度主要衡量一个算法运行所需要的额外空间。
在计算机发展的早期,计算机的存储容量很小。所以对空间复杂度很是在乎。
但是经过计算机行业的迅速发展,计算机的存储容量已经达到了很高的程度。
所以我们如今已经不需要再特别关注一个算法的空间复杂度。
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
2 . 时间复杂度
(1). 时间复杂度的概念:
在计算机科学中,算法的时间复杂度是一个函数,它定量描述了该算法的运行时间。
一个算法执行所耗费的时间,从理论上说,是不能算出来的,
只有你把你的程序放在机器上跑起来,才能知道。
但是我们需要每个算法都上机测试吗?是可以都上机测试,但是这很麻烦,
所以才有了时间复杂度这个分析方式。
一个算法所花费的时间与其中语句的执行次数成正比例,
算法中的基本操作的执行次数,为算法的时间复杂度。
即:
找到某条基本语句与问题规模N之间的数学表达式,就是算出了该算法的时间复杂度。
图例:Func1执行的基本操作次数
上图得到的Func1执行的基本次数为:
F(N) = N^2 + 2*N +10
但实际我们计算时间复杂度时,我们其实并不一定要计算精确的执行次数,
而只需要大概执行次数,那么这里我们使用大O的渐进表示法。
(2). 大O的渐进表示法:
大O符号(Big O notation):是用于描述函数渐进行为的数学符号。
推导大O阶方法:
1、用常数1取代运行时间中的所有加法常数。
2、在修改后的运行次数函数中,只保留最高阶项。
3、如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶。
使用大O的渐进表示法以后,
F(N) = N^2 + 2*N +10
第一步:+10 变为 +1
第二步:保留最高阶项 N^2
第三步:最高项相乘常数为1,不用去除
所以Func1的时间复杂度:O(N^2)
N = 10 F(N) = 100
N = 100 F(N) = 10000
N = 1000 F(N) = 1000000
通过上面我们会发现大O的渐进表示法去掉了那些对结果影响不大的项,
简洁明了的表示出了执行次数。
大O的渐进表示法本质计算的是算法属于哪个量级。
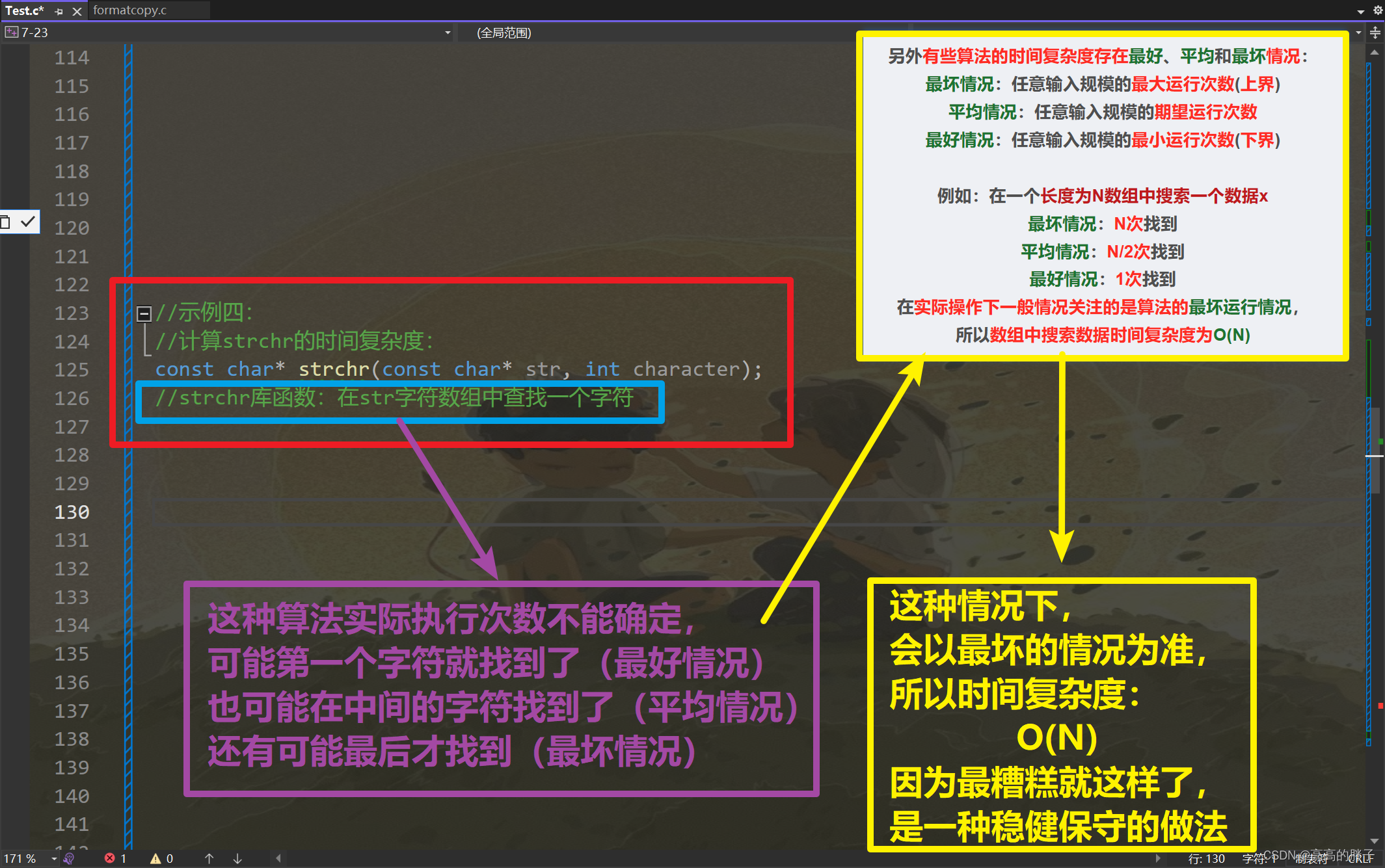
另外有些算法的时间复杂度存在最好、平均和最坏情况:
(可查看下方案例四)
最坏情况:任意输入规模的最大运行次数(上界)
平均情况:任意输入规模的期望运行次数
最好情况:任意输入规模的最小运行次数(下界)
例如:在一个长度为N数组中搜索一个数据x
最坏情况:N次找到
平均情况:N/2次找到
最好情况:1次找到
在实际操作下一般情况关注的是算法的最坏运行情况,
所以数组中搜索数据时间复杂度为O(N)
(3). 常见时间复杂度计算案例:
案例一:
//示例一: //计算Func2的时间复杂度: void Func2(int N) {int count = 0;for (int k = 0; k < 2*N; ++k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count); }图示:
案例二:
//示例二: //计算Func3的时间复杂度: void Func3(int N, int M) {int count = 0;for (int k = 0; k < M; ++k){++count;}for (int k = 0; k < N; k++){++count;}printf("%d\n", count); }图示:
案例三:
//示例三: //计算Func4的时间复杂度: void Func4(int N) {int count = 0;for (int k = 0; k < 100; ++k){++count;}printf("%d\n", count + N); }图示:“cpu技术太强了”
案例四:
//示例四: //计算strchr的时间复杂度: const char* strchr(const char* str, int character); //strchr库函数:在str字符数组中查找一个字符图示:
案例五:
//示例五: #include <stdio.h> //计算BubbleSort的时间复杂度: void BubbleSort(int* a, int n) {assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchange = 1;}}if (exchange == 0){break;}} }图示:
案例六:
//示例六: //计算BinarySearch的时间复杂度: int BinarySearch(int* a, int n, int x) {assert(a);int begin = 0;int end = n - 1;// [begin, end]:begin和end是左闭右闭区间,因此有=号while (begin <= end){int mid = begin + ((end - begin) >> 1);if (a[mid] < x){begin = mid + 1;}else if (a[mid] > x){end = mid - 1;}else{return mid;}}return -1; }图示:
案例七:
//示例七: //计算阶乘递归Fac的时间复杂度: long long Fac(size_t N) {if (0 == N){return 1;}return Fac(N-1)*N; }图示:
案例八:
//示例八: //计算斐波那契递归Fib的时间复杂度: long long Fib(size_t N) {if (N < 3){return 1;}return Fib(N - 1) + Fib(N - 2); }图示:
(4). 常见时间复杂度对比
一般算法常见的复杂度如下表:
5201314 O(1) 常数阶 3n + 4 O(n) 线性阶 3n^2 + 4n + 5 O(n^2) 平方阶 3log(2)n + 4 O(logn) 对数阶 2n + 3nlog(2)n + 14 O(nlogn) nlogn阶 n^3 + 2n^2 + 4n + 6 O(n^3) 立方阶 2^n O(2^n) 指数阶
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
3 . 空间复杂度
(1). 空间复杂度的概念:
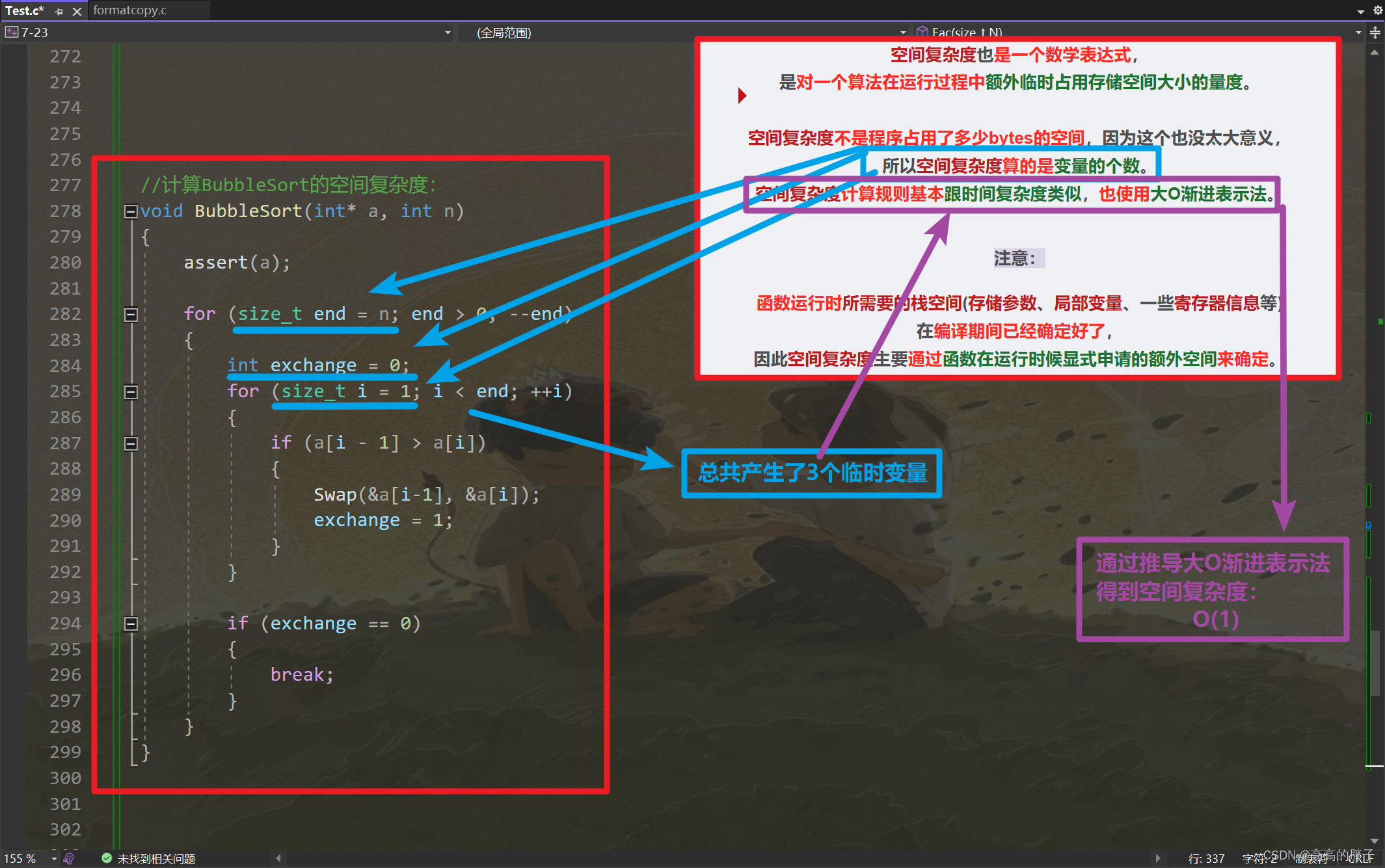
空间复杂度也是一个数学表达式,
是对一个算法在运行过程中额外临时占用存储空间大小的量度。
空间复杂度不是程序占用了多少bytes的空间,因为这个也没太大意义,
所以空间复杂度算的是变量的个数。
空间复杂度计算规则基本跟时间复杂度类似,也使用大O渐进表示法。
注意:
函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)
在编译期间已经确定好了,
因此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定。
(2). 常见空间复杂度计算案例:
案例一:
//计算BubbleSort的空间复杂度: void BubbleSort(int* a, int n) {assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i - 1] > a[i]){Swap(&a[i-1], &a[i]);exchange = 1;}}if (exchange == 0){break;}} }图示:
案例二:
//计算Fibonacci的空间复杂度: //返回斐波那契数列的前n项 long long* Fibonacci(size_t n) {if (n==0){return NULL;}long long* fibArray = (long long*)malloc((n + 1) * sizeof(long long));fibArray[0] = 0;fibArray[1] = 1;for (int i = 2; i <= n; ++i){fibArray[i] = fibArray[i - 1] + fibArray[i - 2];}return fibArray; }图示:
案例三:
//计算阶乘递归Fac的空间复杂度: long long Fac(size_t N) {if (N == 0){return 1;}return Fac(N-1)*N; }图示:
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
4 . 复杂度的oj练习
(1). 时间复杂度练习:消失的数字
对应链接:
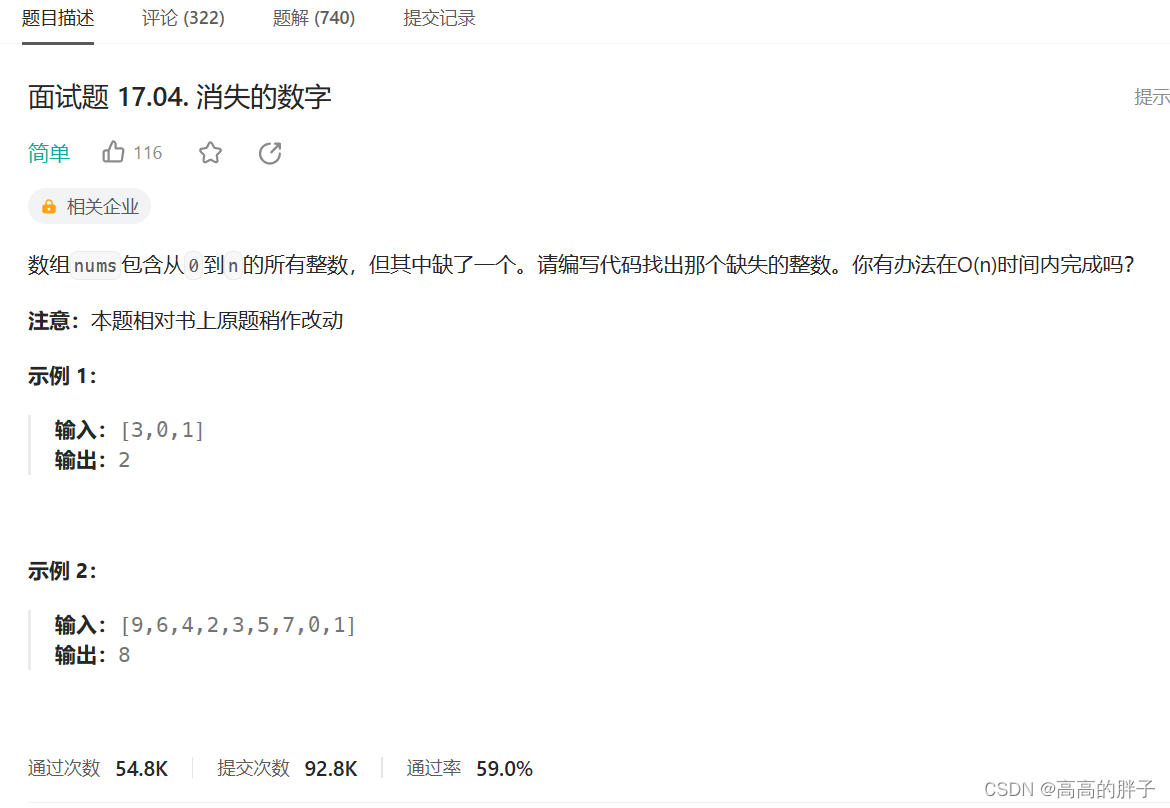
面试题 17.04. 消失的数字 - 力扣(LeetCode)
题目:
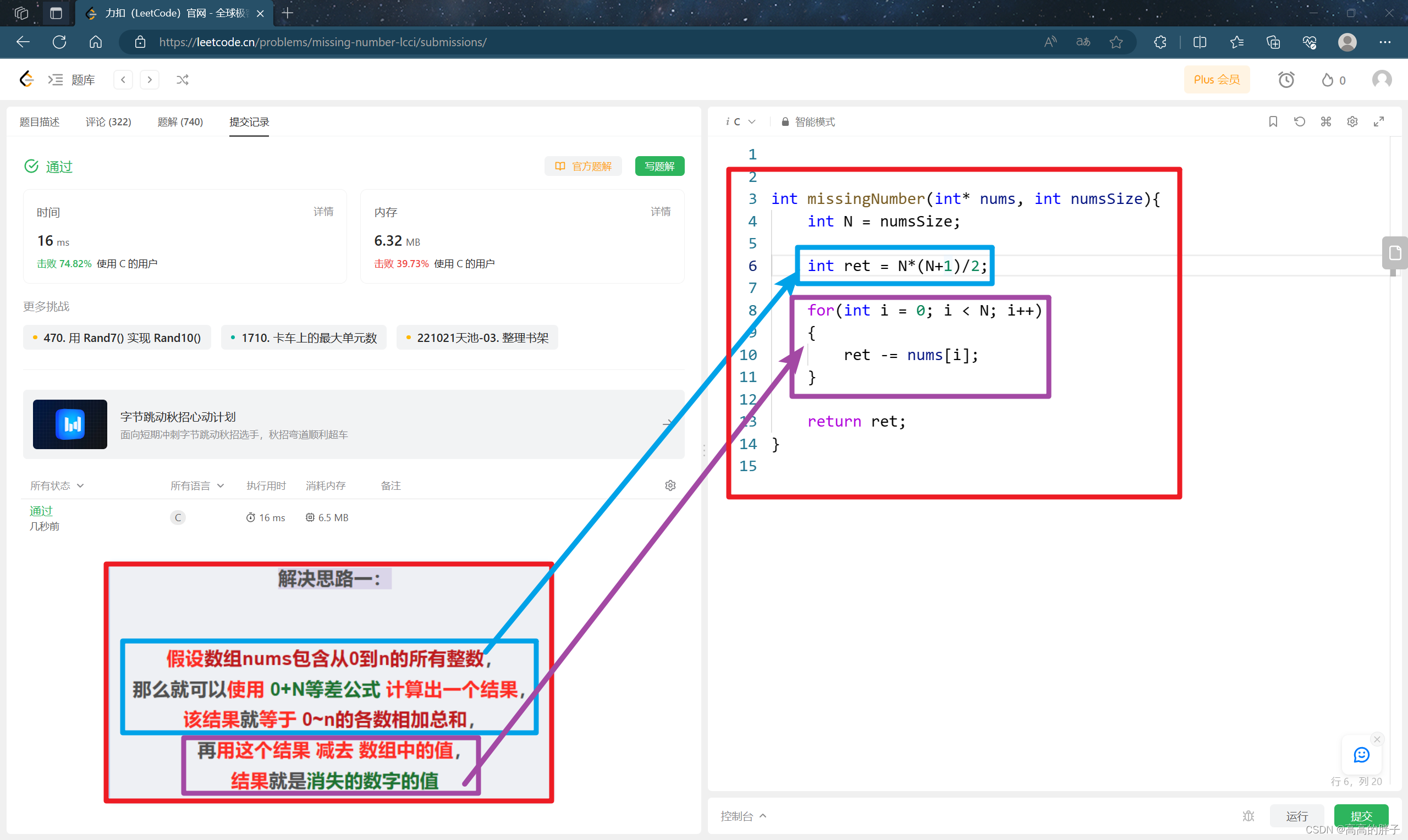
解决思路一:使用等差数列公式
假设数组nums包含从0到n的所有整数,
那么就可以使用 0+N等差公式 计算出一个结果,
该结果就等于 0~n的各数相加总和,
再用这个结果 减去 数组中的值,
结果就是消失的数字的值
图示:
对应代码:
int missingNumber(int* nums, int numsSize){int N = numsSize;int ret = N*(N+1)/2;for(int i = 0; i < N; i++){ret -= nums[i];}return ret; }
解决思路二:异或法
先用 0 异或 完整的0~N各值,
再用该异或的结果来 异或 nums数组(少一个值)
因为异或后相同为0,相异为1,
此时两对值中相同的值就会异或为0,
nums少的一个值异或后就会得到该值
图示:
对应代码:
int missingNumber(int* nums, int numsSize){int N = numsSize;int x = 0; //用来保存异或后的结果for(int i = 0; i <= N; ++i){x ^= i;}for(int i = 0; i < N; ++i){x ^= nums[i];}return x; }
(2). 空间复杂度练习:轮转数组
对应链接:
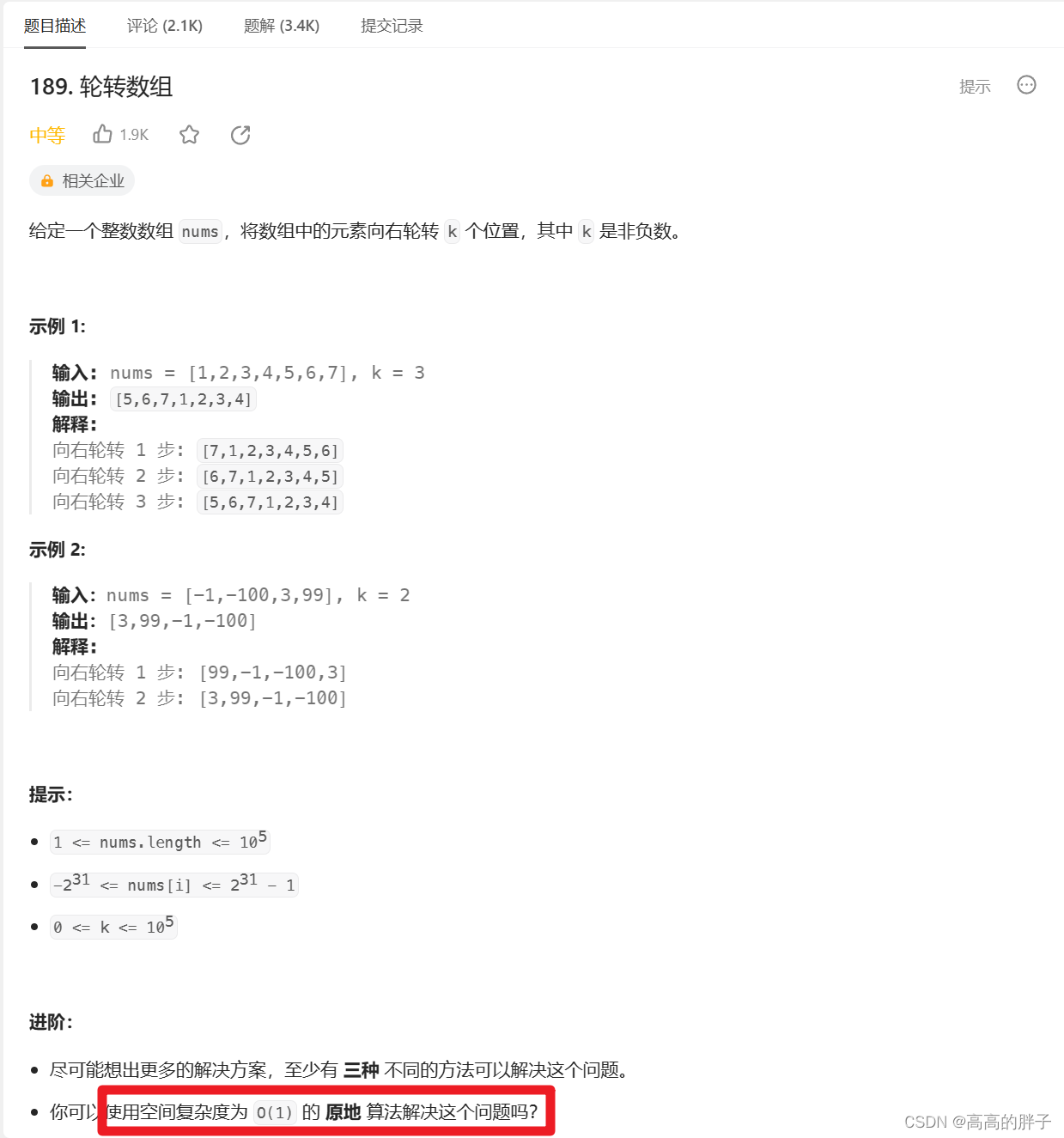
189. 轮转数组 - 力扣(LeetCode)
题目:要求时间复杂度为O(N),空间复杂度为为O(1)
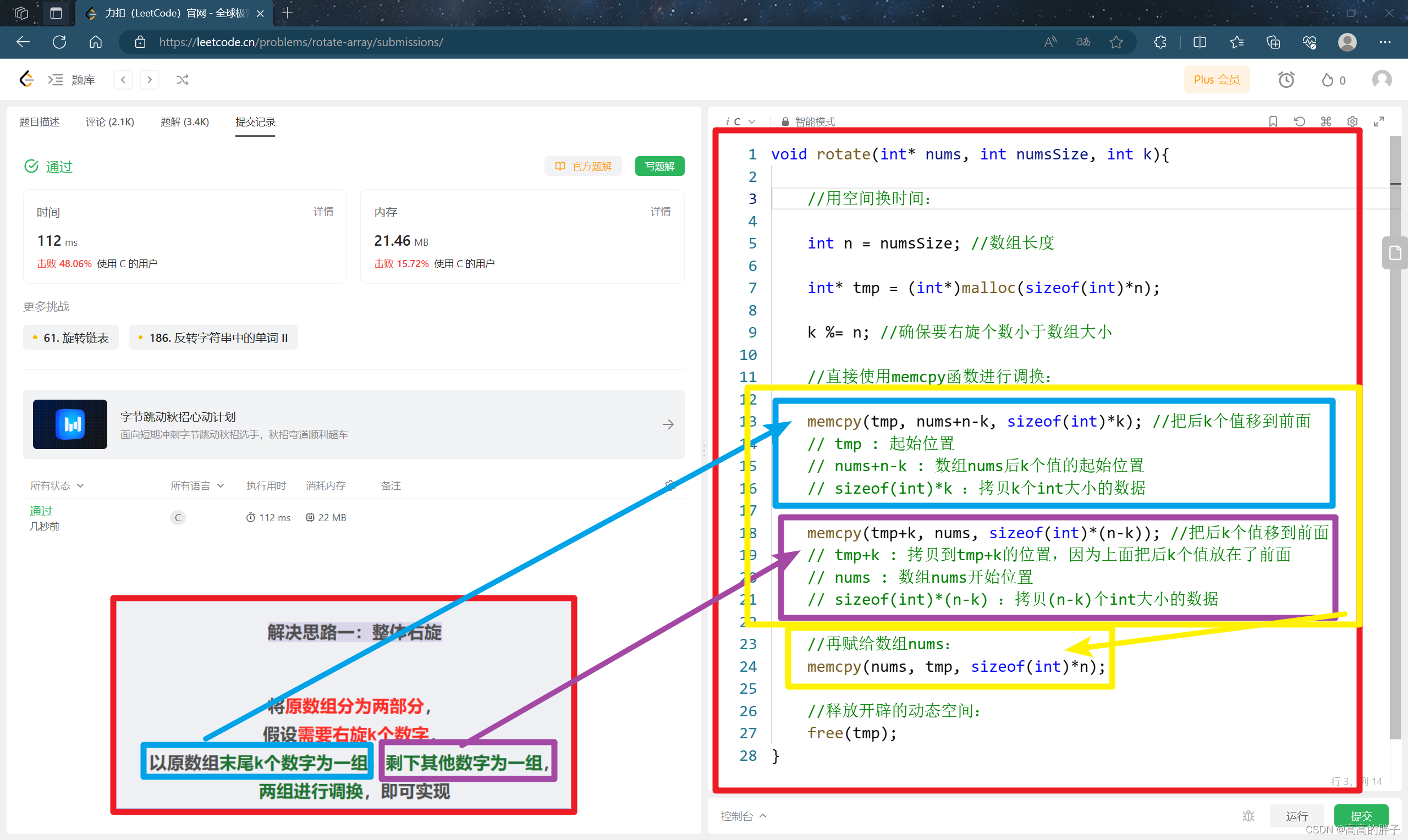
解决思路一:整体右旋
将原数组分为两部分,
假设需要右旋k个数字,
以原数组末尾k个数字为一组,剩下其他数字为一组,
两组进行调换,即可实现
图示:
对应代码:
void rotate(int* nums, int numsSize, int k){//用空间换时间:int n = numsSize; //数组长度int* tmp = (int*)malloc(sizeof(int)*n);k %= n; //确保要右旋个数小于数组大小//直接使用memcpy函数进行调换:memcpy(tmp, nums+n-k, sizeof(int)*k); //把后k个值移到前面// tmp : 起始位置// nums+n-k : 数组nums后k个值的起始位置// sizeof(int)*k :拷贝k个int大小的数据memcpy(tmp+k, nums, sizeof(int)*(n-k)); //把后k个值移到前面// tmp+k : 拷贝到tmp+k的位置,因为上面把后k个值放在了前面// nums : 数组nums开始位置// sizeof(int)*(n-k) :拷贝(n-k)个int大小的数据//再赋给数组nums:memcpy(nums, tmp, sizeof(int)*n);//释放开辟的动态空间:free(tmp); }
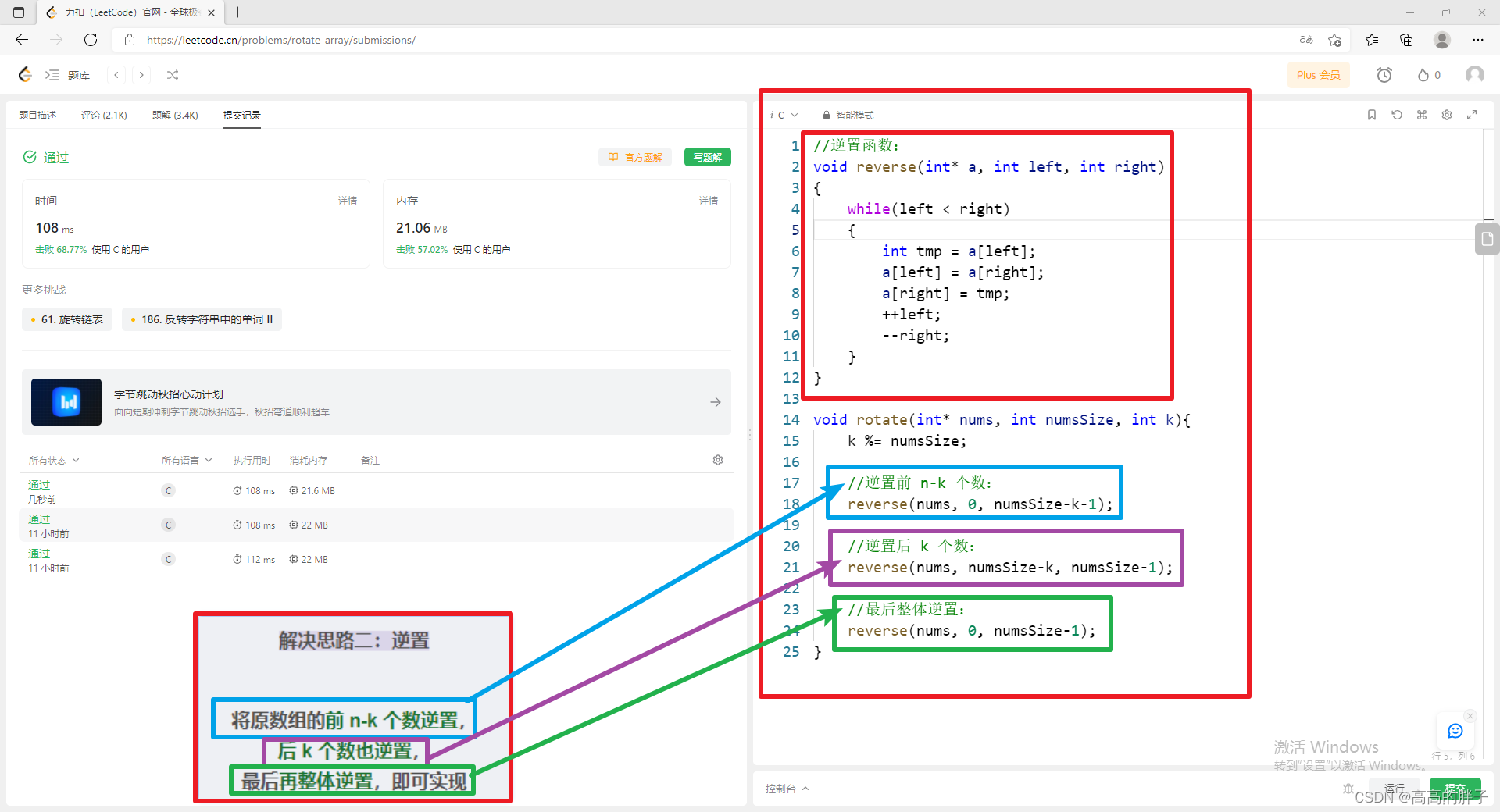
解决思路二:逆置
将原数组的前 n-k 个数逆置,
后 k 个数也逆置,
最后再整体逆置,即可实现
图示:
对应代码:
//逆置函数: void reverse(int* a, int left, int right) {while(left < right){int tmp = a[left];a[left] = a[right];a[right] = tmp;++left;--right;} }void rotate(int* nums, int numsSize, int k){k %= numsSize;//逆置前 n-k 个数:reverse(nums, 0, numsSize-k-1);//逆置后 k 个数:reverse(nums, numsSize-k, numsSize-1);//最后整体逆置:reverse(nums, 0, numsSize-1); }
相关文章:
【数据结构初阶】一. 复杂度讲解
相关代码gitee自取: C语言学习日记: 加油努力 (gitee.com) 接上期: 学C的第三十四天【程序环境和预处理】_高高的胖子的博客-CSDN博客 1 . 算法效率 (1). 什么是数据结构: 数据结构(Data Structure)是计算机存储、…...
Jmete+Grafana+Prometheus+Influxdb+Nginx+Docker架构搭建压测体系/监控体系/实时压测数据展示平台+遇到问题总结
背景 需要大批量压测时,单机发出的压力能力有限,需要多台jmeter来同时进行压测;发压机资源不够,被压测系统没到瓶颈之前,发压机难免先发生资源不足的情形;反复压测时候也需要在不同机器中启动压测脚本&…...

php提交表单将html相互字符转化的封装函数
在 PHP 中,您可以使用 htmlspecialchars() 函数将 HTML 字符转换为文本。该函数将把 <、>、" 和 等特殊字符转换为对应的 HTML 实体,从而避免跨站点脚本(XSS)攻击。 例如,如果您有一个表单输入字段的值&a…...

7 Series FPGAs GTX/GTH Transceivers
目录 1. Overview2. Block Diagram3. Transmitter4. Receiver5. Physical Coding Sublayer(PCS)6. Physical Medium Attachment(PMA)本博客为Xilinx 7系列FPGA的千兆比特高速收发器(Gigabit Transceiver, GT)介绍 ug476 - 7 Series FPGAs GTX GTH TransceiversUser Guide…...

iOS系统下轻松构建自动化数据收集流程
在当今信息爆炸的时代,我们经常需要从各种渠道获取大量的数据。然而,手动收集这些数据不仅耗费时间和精力,还容易出错。幸运的是,在现代科技发展中有两个强大工具可以帮助我们解决这一问题——Python编程语言和iOS设备上预装的Sho…...

Android基础之Activity生命周期
Activity是Android四大组件之一、称为之首也恰如其分。 Activity直接翻译为中文叫活动。在Android系统中Activity就是我看到的一个完整的界面。 界面中看到的TextView(文字)、Button(按钮)、ImageView(图片)都是需要Activity来承载的。 总…...
:安装和使用方法)
Golang 程序漏洞检测利器 govulncheck(一):安装和使用方法
govulncheck 是什么? govulncheck 是一个命令行工具,可以帮助 Golang 开发者快速找到项目代码和依赖的模块中的安全漏洞。该工具可以分析源代码和二进制文件,识别代码中对这些漏洞的任何直接或间接调用。 默认情况下,govulnchec…...

强化学习算法总结 2
强化学习算法总结 2 4.动态规划 待解决问题分解成若干个子问题,先求解子问题,然后得到目标问题的解 需要知道整个状态转移函数和价值函数,状态空间离散且有限 策略迭代: 策略评估:贝尔曼期望方程来得到一个策略的 V ( s ) V(s…...

修改node_modules避免更新覆盖 patch-package
说明:直接修改第三方库的代码,会带来团队协作的问题,使用patch-package生成补丁包 什么是 patch-package? patch-package 是一个基于 Git 的工具,它可以帮助我们对依赖包进行修复补丁。通过创建一个与问题相关的补丁文…...
Elasticsearch安装,Springboot整合Elasticsearch详细教程
Elasticsearch 是一个分布式、RESTful 风格的搜索和数据分析引擎,能够实现近乎实时的搜索。 Elasticsearch官网https://www.elastic.co/cn/ 这篇文章主要简单介绍一下Elasticsearch,Elasticsearch的java API博主也在学习中,文章会持续更新~ …...
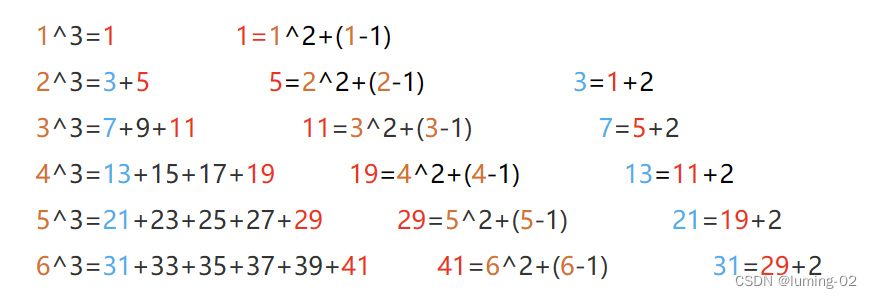
OJ题库:计算日期到天数转换、打印从1到最大的n位数 、尼科彻斯定理
前言:在部分大厂笔试时经常会使用OJ题目,这里对《华为机试》和《剑指offer》中的部分题目进行思路分析和讲解,希望对各位读者有所帮助。 题目来自牛客网,欢迎各位积极挑战: HJ73:计算日期到天数转换_牛客网 JZ17:打印…...
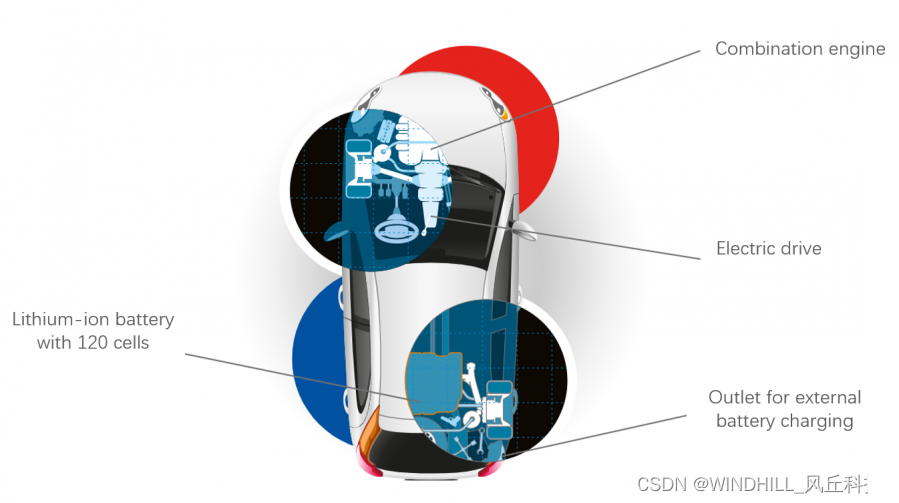
混合动力汽车耐久测试
一 背景 整车厂可通过发动机和电机驱动的结合为多款车型提供混合动力驱动技术。汽车集成电机驱动可大大减少二氧化碳的排放,不仅如此,全电动驱动或混合动力驱动的汽车还将使用户体验到更好的驾驶感受,且这种汽车可通过电动机来实现更快的加速…...
useRef 定义的 ref 在控制台可以打印但是页面不生效?
useRef 是一个 React Hook,它能让你引用一个不需要渲染的值。 点击计时器 点击按钮后在控制台可以打印但是页面不生效。 useRef 返回的值在函数组件中不会自动触发重新渲染,所以控制台可以显示变化而按钮上无法显示 ref.current的变化。 import { use…...
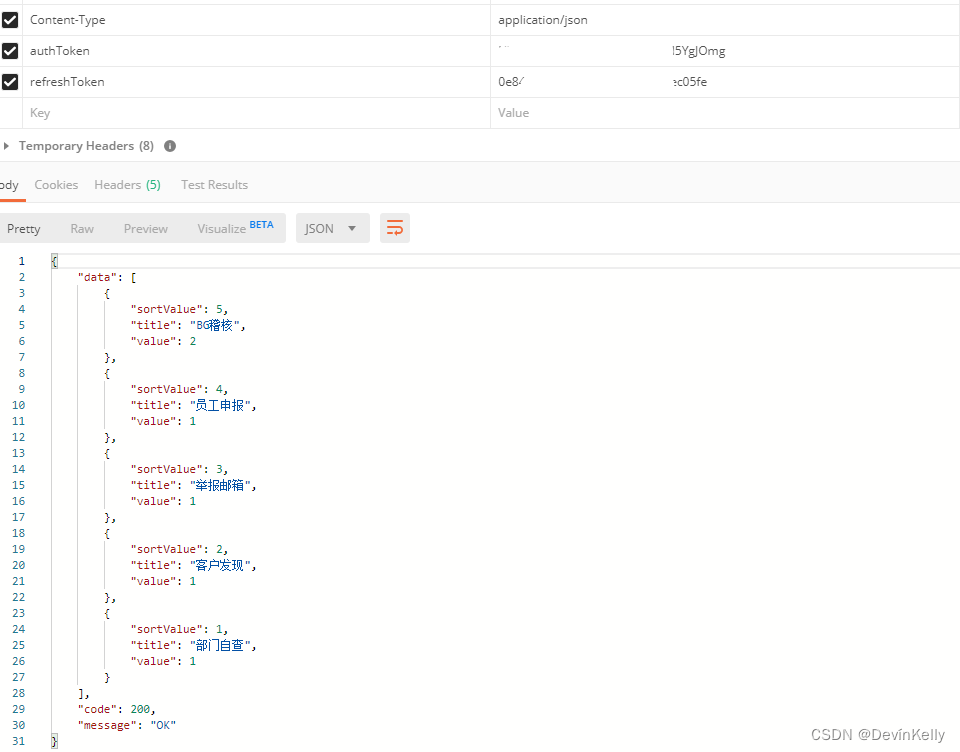
【Java 动态数据统计图】动态数据统计思路案例(动态,排序,动态数组(重点推荐))七(129)
需求:前端根据后端的返回数据:画统计图; 说明: 1.X轴为地域,Y轴为地域出现的次数; 2. 动态展示(有地域展示,没有不展示,且高低排序) Demo案例: …...

Cell Reports | 揭开METTL14在介导m6A修饰中的神秘面纱
m6A被认为是最丰富的mRNA修饰,广泛分布在大多数真核生物中,包括哺乳动物、植物、昆虫、酵母和某些病毒。m6A修饰的沉积和去除之间的动态平衡对于正常的生物过程和发育至关重要,如失调通常与癌症等疾病有关。m6A修饰由m6A甲基转移酶复合物&…...

297. 二叉树的序列化与反序列化
题目描述 序列化是将一个数据结构或者对象转换为连续的比特位的操作,进而可以将转换后的数据存储在一个文件或者内存中,同时也可以通过网络传输到另一个计算机环境,采取相反方式重构得到原数据。 请设计一个算法来实现二叉树的序列化与反序…...
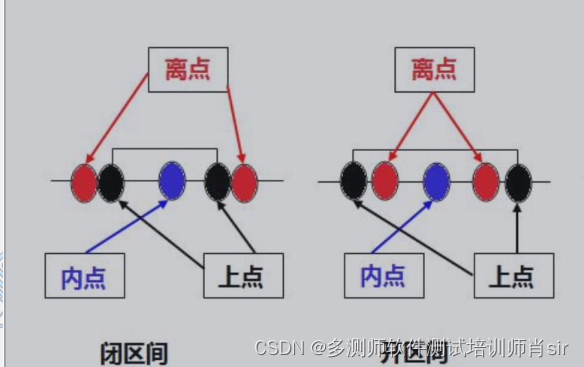
肖sir__设计测试用例方法之边界值03_(黑盒测试)
设计测试用例方法之边界值 边界点定义 上点:边界上的点 离点:离上点最近的点(即上点左右两边最邻近的点) 内点:在域范围内的点 案例:qq号:5-12位 闭区间: 离点:5 位 &…...

功能测试常用的测试用例大全
登录、添加、删除、查询模块是我们经常遇到的,这些模块的测试点该如何考虑 1)登录 ① 用户名和密码都符合要求(格式上的要求) ② 用户名和密码都不符合要求(格式上的要求) ③ 用户名符合要求,密码不符合要求(格式上的要求) ④ 密码符合要求,…...

css利用flex分配剩余高度出现子组件溢出问题
1.利用flex分配剩余高度/宽度 情景:父组件高度一定,子组件中,其他子组件高度固定,一个子组件高度不确定(页面滚动列表) .father{display: flex;flex-direction: column;.son1{height: 200px;}.son2{//或 …...
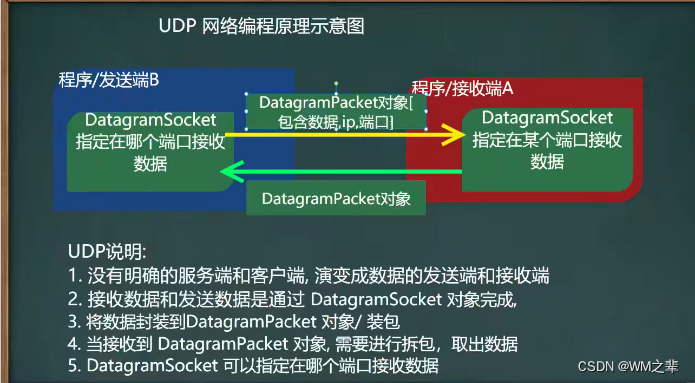
Java中的网络编程------基于Socket的TCP编程和基于UDP的网络编程,netstat指令
Socket 在Java中,Socket是一种用于网络通信的编程接口,它允许不同计算机之间的程序进行数据交换和通信。Socket使得网络应用程序能够通过TCP或UDP协议在不同主机之间建立连接、发送数据和接收数据。以下是Socket的基本介绍: Socket类型&…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...