动手学深度学习(四)多层感知机
目录
一、多层感知机的从零开始实现
1.1 初始化模型参数
1.2 实现Relu函数
1.3 实现模型
1.4 训练
二、多层感知机的简洁实现
2.1 实现模型
2.2 训练
三、模型选择
3.1 训练误差和泛化误差
3.2 验证数据集和测试数据集
3.3 过拟合和欠拟合
3.4 代码实现
3.4.1 生成训练和测试数据的标签
3.4.2 评估损失
3.4.3 训练函数
3.4.4 正常拟合(使用三阶多项式函数的数据特征)
3.4.5 欠拟合(使用线性函数的数据特征)
3.4.6 过拟合(使用高阶多项式函数的数据特征)
四、权重衰减
4.1 范数与权重衰减
4.2 代码实现
4.2.1 生成数据
4.2.2 初始化模型参数
4.2.3 定义L2范数惩罚 (核心)
4.2.4 训练函数
4.2.5 训练
4.2.6 简洁实现
五、数值稳定性和模型初始化
经过了多层感知机后,相当于将原始的特征转化成了新的特征,或者说提炼出更合适的特征,这就是隐藏层的作用。
from:清晰理解多层感知机和反向传播 - 知乎
一、多层感知机的从零开始实现
import torch
from torch import nn
from d2l import torch as d2lbatch_size = 256 # 批量大小
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size) # 读取数据集
1.1 初始化模型参数
实现一个具有隐藏层的多层感知机,它包含256个隐藏单元。
# 初始化模型参数
num_inputs, num_outputs, num_hiddens = 784, 10, 256 # 输入特征数量,输出类别,隐藏单元W1 = nn.Parameter(torch.randn(num_inputs, num_hiddens, requires_grad=True) * 0.01) # 第一层的权重矩阵
b1 = nn.Parameter(torch.zeros(num_hiddens, requires_grad=True)) # 第一层的偏置向量W2 = nn.Parameter(torch.randn(num_hiddens, num_outputs, requires_grad=True) * 0.01) # 第二层的权重矩阵
b2 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True)) # 第二层的偏置向量
params = [W1, b1, W2, b2] # nn.Parameter为需要优化的张量分配地址空间nn.Parameter()是PyTorch中用于定义可训练参数的类。在神经网络模型中,我们可以通过定义nn.Parameter()来创建需要优化的可训练的张量。
1.2 实现Relu函数
# 实现Relu激活函数
def relu(X):a = torch.zeros_like(X)return torch.max(X, a)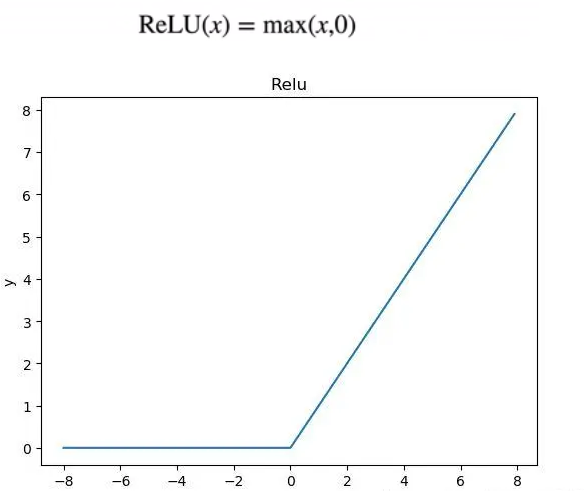
1.3 实现模型
# 实现模型
def net(X):X = X.reshape((-1, num_inputs)) # 将图像拉伸为长度为num_inputs的向量H = relu(X @ W1 + b1) # @为矩阵乘法,输出为长度为num_hiddens的向量,传入下一层return (H @ W2 + b2)loss = nn.CrossEntropyLoss() # 交叉熵损失1.4 训练
# 训练
num_epochs, lr = 10, 0.1
updater = torch.optim.SGD(params, lr=lr) # 定义优化算法
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, updater)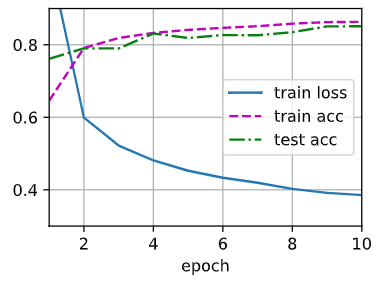
二、多层感知机的简洁实现
引用API更简洁实现多层感知机。
import torch
from torch import nn
from d2l import torch as d2l2.1 实现模型
# 实现模型
net = nn.Sequential(nn.Flatten(), nn.Linear(784, 256), nn.ReLU(), nn.Linear(256, 10)) # 隐藏层有256个单元def init_weights(m): # 初始化参数if type(m) == nn.Linear:nn.init.normal_(m.weight, std=0.01)net.apply(init_weights)2.2 训练
# 训练
batch_size, lr, num_epochs = 256, 0.1, 10loss = nn.CrossEntropyLoss(reduction='none') # 交叉熵损失
trainer = torch.optim.SGD(net.parameters(), lr=lr) # 优化算法
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size) # 传入数据d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)三、模型选择
3.1 训练误差和泛化误差
训练误差:模型在训练数据上的误差。
泛化误差(测试误差):模型在新数据上的误差。(我们着重关心的)
例子︰根据摸考成绩来预测未来考试分数。
在过去的考试中表现很好(训练误差)不代表未来的考试一定会好(泛化误差)。
3.2 验证数据集和测试数据集
验证数据集:验证数据集(Validation Datasets)是训练模型时所保留的数据样本,我们在调整模型超参数时,需要根据它来对模型的能力进行评估。(一个用来评估模型好坏的数据集)
测试数据集:测试数据集(Test Datasets)是一个在建模阶段没有使用过的数据集。一旦根据验证数据集确定了“最好”的模型,那么在测试集上对模型的性能评估。(只用一次的数据集)
Q:为什么要设立验证数据集?
A:如果我们在模型选择的过程中使用测试数据,可能会有过拟合测试数据的风险。
K折交叉验证:在没有足够的多数据时使用(这是常态)
算法:
- 将训练数据分割成K块
- For i = 1,2,…,K
- 使用第 i 块作为验证数据集,其余的作为训练数据集
- 报告K个验证集误差的平均
常用:K=5或10。
3.3 过拟合和欠拟合

过拟合:训练误差明显小于验证误差。(这不一定是坏事,深度学习领域预测模型在训练集上的表现往往在验证集上的表现好得多)
欠拟合:训练误差和验证误差之间的差距很小,而且误差值都很大,需要寻找更复杂的模型来减小训练误差。
1. 模型容量(模型复杂性)

- 拟合各种函数的能力
- 低容量的模型难以拟合训练数据
- 高容量的模型可以记住所有的训练数据
(一般取泛化误差最小的模型容量为最优)
2. 比较模型容量
难以在不同种类算法之间比较。
- 例如树模型和神经网络
给定一个模型种类,有两个主要因素:
- 参数的个数
- 参数值的选择范围
3. 数据的复杂度
因素:
- 样本个数
- 每个样本的元素个数
- 时间、空间结构
- 多样性(多少类的分类)
3.4 代码实现
import math
import numpy as np
import torch
from torch import nn
from d2l import torch as d2lmax_degree = 20 # 多项式的最大阶数
n_train, n_test = 100, 100 # 训练数据和测试数据的大小
true_w = np.zeros(max_degree) # 初始化权重参数w,均为0
true_w[:4] = np.array([5, 1.2, -3.4, 5.6]) # 参数w前四个的取值,用作充当真实值3.4.1 生成训练和测试数据的标签
使用以下三阶多项式来生成训练和测试数据的标签:
![]()
# 生成训练和测试数据的标签
features = np.random.normal(size=(n_train + n_test, 1)) # 随机正态分布生成数据集样本
np.random.shuffle(features) # 打乱数据集
poly_features = np.power(features,np.arange(max_degree).reshape(1, -1)) # 按列表下标依次求1到20次幂
for i in range(max_degree):poly_features[:, i] /= math.gamma(i + 1) # gamma(n)=(n-1)!labels = np.dot(poly_features, true_w) # 作点积运算,求结果y
labels += np.random.normal(scale=0.1, size=labels.shape) # 随机正态分布生成偏置项# numpy ndarray转换为tensor
true_w, features, poly_features, labels = [torch.tensor(x, dtype=torch.float32) for x in [true_w, features, poly_features, labels]]3.4.2 评估损失
def evaluate_loss(net, data_iter, loss):"""评估给定数据集上模型的损失"""metric = d2l.Accumulator(2) # 累加器,存放模型总损失、样本总数for X, y in data_iter:out = net(X)y = y.reshape(out.shape)l = loss(out, y)metric.add(l.sum(), l.numel()) # 将损失值总和和样本总数添加入累加器return metric[0] / metric[1] # 返回平均损失3.4.3 训练函数
# 训练函数
def train(train_features, test_features, train_labels, test_labels, num_epochs=400):loss = nn.MSELoss(reduction='none') # 平方误差损失函数input_shape = train_features.shape[-1]net = nn.Sequential(nn.Linear(input_shape, 1, bias=False)) # 线性层batch_size = min(10, train_labels.shape[0]) train_iter = d2l.load_array((train_features, train_labels.reshape(-1, 1)),batch_size)test_iter = d2l.load_array((test_features, test_labels.reshape(-1, 1)),batch_size, is_train=False)trainer = torch.optim.SGD(net.parameters(), lr=0.01) #小批量随机梯度下降优化算法animator = d2l.Animator(xlabel='epoch', ylabel='loss', yscale='log',xlim=[1, num_epochs], ylim=[1e-3, 1e2],legend=['train', 'test'])for epoch in range(num_epochs):d2l.train_epoch_ch3(net, train_iter, loss, trainer)if epoch == 0 or (epoch + 1) % 20 == 0:animator.add(epoch + 1, (evaluate_loss(net, train_iter, loss),evaluate_loss(net, test_iter, loss)))print('weight:', net[0].weight.data.numpy())
3.4.4 正常拟合(使用三阶多项式函数的数据特征)
我们将首先使用三阶多项式函数,它与数据生成函数的阶数相同。 结果表明,该模型能有效降低训练损失和测试损失。 学习到的模型参数也接近真实值w=[5,1.2,−3.4,5.6] 。
# 训练
# 拟合(正常),给足训练特征和验证特征
train(poly_features[:n_train, :4], poly_features[n_train:,:4], # 多项式特征[200,20],前4列中,前100行划为训练集,后100行划为验证集labels[:n_train], labels[n_train:])weight: [[ 5.0149393 1.2182785 -3.4234915 5.535555 ]],已学习到的模型参数也接近真实值w=[5, 1.2, -3.4, 5.6]。
poly_features,为多项式特征矩阵,大小为[200,20],列数为多项式的阶数。
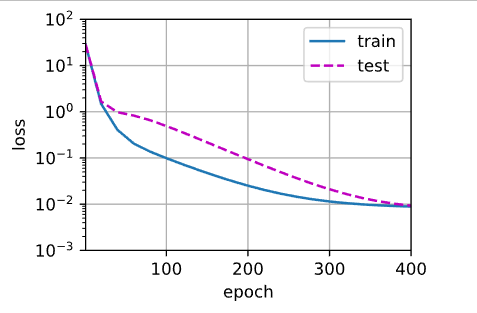
3.4.5 欠拟合(使用线性函数的数据特征)
线性函数的数据训练三阶多项式模型,模型过于复杂,数据多样性不够或过少导致欠拟合。
# 欠拟合,训练特征和验证特征减半
train(poly_features[:n_train, :2], poly_features[n_train:,:2],labels[:n_train], labels[n_train:])
3.4.6 过拟合(使用高阶多项式函数的数据特征)
高阶多项式的数据训练三阶多项式模型,数据特征过于复杂(或过多),模型不足以支撑,导致数据中的噪声一并学习到,使得到最后产生了过拟合,训练损失可以有效地降低,但测试损失仍然很高。
# 过拟合,从多项式特征中选取所有维度
train(poly_features[:n_train, :], poly_features[n_train:,:],labels[:n_train], labels[n_train:], num_epochs=1500)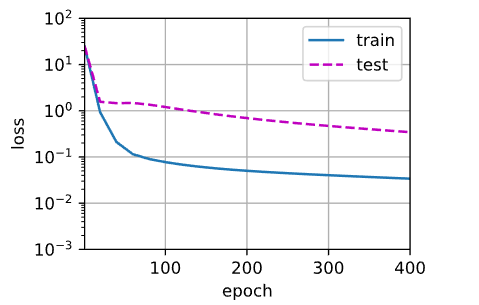
四、权重衰减
“范数”参考:动手学深度学习(一)预备知识_向岸看的博客-CSDN博客
Q:为什么要引入惩罚项?
A:为防止模型过拟合,提高模型的泛化能力,通常会在损失函数的后面添加一个正则化项。
L1正则化和L2正则化可以看做是损失函数的惩罚项。所谓惩罚是指对损失函数中的某些参数做一些约束,使得参数的自由度变小。Q:正则化在深度学习中含义是指什么?
A:正则化其实是一种策略,以增大训练误差为代价来减少测试误差的所有策略我们都可以称作为正则化。换句话说就是正则化是为了防止模型过拟合。L2范数就是最常用的正则化方法之一。
4.1 范数与权重衰减
权重衰退通过L2正则项使得模型参数不会过大,从而控制模型复杂度 。
使用均方范数作为硬性限制。通过限制参数值 的选择范围来控制模型的复杂度。
![]()
对每个 ,都可以找到
使得之前的目标函数等价于下面,实际上这是最小预测损失和惩罚项之和:
![]()
超参数 控制了正则项的重要程度,

增加了惩罚项(L2范数)后,计算梯度的公式:
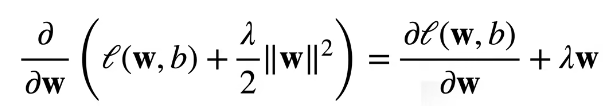
更新参数的公式:

通常 ,在深度学习中通常叫做权重衰退。
Q:为什么叫做权重衰退?
A:可见公式中,
,每次更新权重之前,先将权重缩小一次。权重衰退通过L2正则项使得模型参数不会过大,从而控制模型复杂度。正则项权重是控制模型复杂度的超参数。
4.2 代码实现
"""导入相关库"""
import torch
from d2l import torch as d2l
from torch import nn4.2.1 生成数据
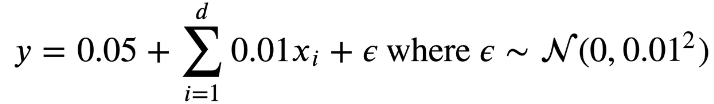
""" 生成数据集 """
n_train, n_test, num_inputs, batch_size = 50, 100, 200, 5 # 训练集,验证集,输入变量,以及batch的大小
true_w, true_b = torch.ones((num_inputs, 1)) * 0.01, 0.1 # 定义参数,偏置项
train_data = d2l.synthetic_data(true_w, true_b, n_train) # 生成数据
test_data = d2l.synthetic_data(true_w, true_b, n_test)
train_iter = d2l.load_array(train_data, batch_size)
test_iter = d2l.load_array(test_data, batch_size, is_train=False)4.2.2 初始化模型参数
""" 初始化模型参数 """
def init_params():w = torch.normal(0, 1, size=(num_inputs, 1), requires_grad=True) #从标准正态分布中随机选取b = torch.zeros(1, requires_grad=True) # 偏置初始值为0return [w, b]
4.2.3 定义L2范数惩罚 (核心)
""" 定义L2范数惩罚 """
def l2_penalty(w):return torch.sum(w.pow(2)) / 24.2.4 训练函数
""" 训练函数 """
def train(lambd):w, b = init_params() #初始化参数net, loss = lambda X: d2l.linreg(X, w, b), d2l.squared_lossnum_epochs, lr = 100, 0.003# 绘图animator = d2l.Animator(xlabel='epochs', ylabel='loss', yscale='log',xlim=[5, num_epochs], legend=['train', 'test'])for epoch in range(num_epochs):for X, y in train_iter:# 增加了L2范数惩罚项,# 广播机制使l2_penalty(w)成为一个长度为batch_size的向量l = loss(net(X), y) + lambd * l2_penalty(w)l.sum().backward()d2l.sgd([w, b], lr, batch_size)# 绘制训练误差和测试误差if (epoch + 1) % 5 == 0:animator.add(epoch + 1, (d2l.evaluate_loss(net, train_iter, loss),d2l.evaluate_loss(net, test_iter, loss)))print('w的L2范数是:', torch.norm(w).item())lambda [arg1 [,arg2,.....argn]]:expression
- args:函数将接收的参数。
- expression:结果为函数返回值的表达式。
冒号前是参数,可以有多个,用逗号隔开,冒号右边的为表达式(只能为一个)。其实lambda返回值是一个函数的地址,也就是函数对象。
示例:def sum(x,y):return x+yprint(sum(1,2))# 使用lambda函数:sum = lambda x,y:x+y# 没有了函数sum的定义,又称为匿名函数print(sum(1,2))
4.2.5 训练
先用lambd=0,禁用权重衰退。
""" 训练 """
train(lambd=0)
从上图结果来看,存在严重的过拟合问题,验证误差远大于训练误差。
之后,我们令lambd=5,观察使用权重衰退的效果。
# 使用权重衰退
train(lambd=5)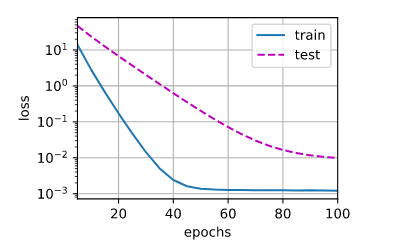
验证误差有明显的下降。
4.2.6 简洁实现
我们在实例化优化器时直接通过weight_decay指定权重衰退超参数,注意偏置项b没有weight_decay,指定了也不会衰退。
trainer = torch.optim.SGD([{"params":net[0].weight,'weight_decay': wd},{"params":net[0].bias}], lr=lr)五、数值稳定性和模型初始化
梯度值的乘积:

- 梯度爆炸:是指当训练深度神经网络时,梯度的值会快速增大,造成参数的更新变得过大,导致模型不稳定,难以训练。
- 梯度消失:是指当训练深度神经网络时,梯度的值会快速减小,导致参数的更新变得很小,甚至无法更新,使得模型难以学习有用的特征。
梯度爆炸的原因:
- 值超出值域(infinity),对于16位浮点数尤为严重(数值区间6e-5 - 6e4)。
- 对学习率敏感。如果学习率太大->大参数值-→更大的梯度·如果学习率太小->训练无进展(我们可能需要在训练过程不断调整学习率)。
梯度消失的原因:
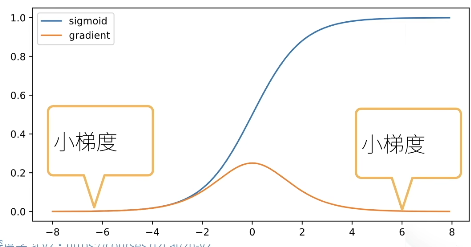
- sigmoid函数是导致梯度消失的一个常见原因。
![]()
由sigmoid的导数可见,当输入值很大或很小时,它的梯度很有可能会等于0,这样就会导致梯度消失。
相关文章:

动手学深度学习(四)多层感知机
目录 一、多层感知机的从零开始实现 1.1 初始化模型参数 1.2 实现Relu函数 1.3 实现模型 1.4 训练 二、多层感知机的简洁实现 2.1 实现模型 2.2 训练 三、模型选择 3.1 训练误差和泛化误差 3.2 验证数据集和测试数据集 3.3 过拟合和欠拟合 3.4 代码实现 3.4.1 生…...
融云出海:社交泛娱乐出海,「从 0 到 1」最全攻略
9 月 21 日,融云直播课社交泛娱乐出海最短变现路径如何快速实现一款 1V1 视频社交应用? 欢迎点击上方小程序报名~ 本期我们翻到《地图》的实践篇,从赛道/品类选择、目标地区适配、用户增长、变现模式、本地化运营、跨国团队管理等方面完整描绘…...

生成式人工智能促使社会转变
作者:JEFF VESTAL 了解 Elastic 如何处于大型语言模型革命的最前沿 – 通过提供实时信息并将 LLM 集成到数据分析的搜索、可观察性和安全系统中,帮助用户将 LLM 提升到新的高度。 iPhone 社会转变:新时代的黎明 曾几何时,不久前…...
【STM32】SPI初步使用 读写FLASH W25Q64
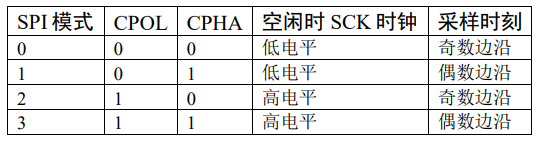
硬件连接 (1) SS( Slave Select):从设备选择信号线,常称为片选信号线,每个从设备都有独立的这一条 NSS 信号线,当主机要选择从设备时,把该从设备的 NSS 信号线设置为低电平,该从设备即被选中,即…...
常用属性)
javaScript:DOM(父子/兄弟)常用属性
目录 前言 一.父子关系 父子关系的常用属性 childNodes 获取所有的子节点 children 获取所有的子元素(dom元素) firstChild 获取元素的第一个子节点,相当于 childNodes[0] firstElementChild 获取元素的第一个元素 相当于 children[0]…...
驱动设备树配置和用法)
笔记:linux中LED(GPIO)驱动设备树配置和用法
设备树中节点配置 设备树中的LED驱动一般是这样写,LED驱动可以控制GPIO的电平变化,生成文件节点很方便 leds: leds {compatible "gpio-leds";gpio_demo: gpio_demo {label "gpio_demo";gpios <&gpio0 RK_PC0 GPIO_ACTIV…...
能耗管理+分区温控成为开发节能、省电神器的关键!从此告别电费刺客时代
取暖器在人们脑海中最深刻的印象,就是费电!而它耗电量大的原因,主要在于它是靠电能直接转化为热能:在取暖设备通电后,内部高电阻的电热丝发热,风机会将这股热量吹散到室内,从而达到全屋取暖的效…...

垃圾回收 - 复制算法
GC复制算法是Marvin L.Minsky在1963年研究出来的算法。说简单点,就是只把某个空间的活动对象复制到其它空间,把原空间里的所有对象都回收掉。这是一个大胆的想法。在此,我们将复制活动对象的原空间称为From空间,将粘贴活动对象的新…...

基于SpringMVC实现常见功能
基于SpringMVC实现常见功能 防止XSS攻击 XSS攻击全称跨站脚本攻击,是为不和层叠样式表(Cascading Style Sheets, CSS)的缩写混淆,故将跨站脚本攻击缩写为XSS,XSS是一种在web应用中的计算机安全漏洞,它允许恶意web用户将代码植入到…...
MetInfo5.0文件包含漏洞
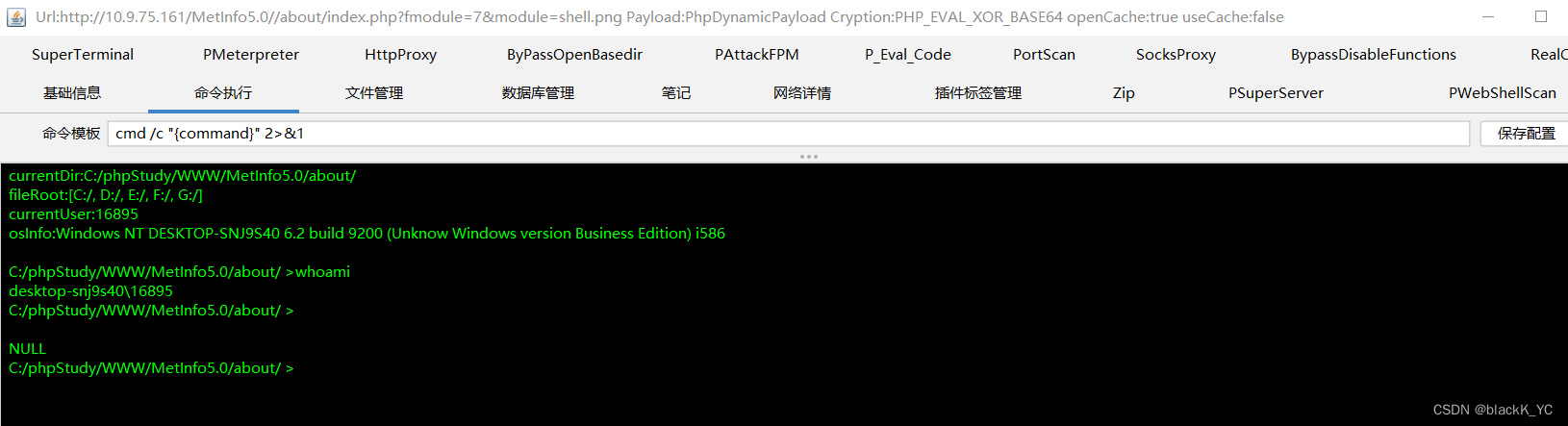
MetInfo历史版本与文件 环境在这里下载,使用phpstudy搭建 我们来看到这个index.php,如下图所示,其中定义了fmodule变量与module变量,其中require_once语句表示将某个文件引入当前文件,在这个代码中,通过r…...

【SpringBoot】SpringBoot实现基本的区块链的步骤与代码
以下是Spring Boot实现基本的区块链代码的步骤: 创建一个Block类,它表示一个区块,包含一个区块头和一个区块体。区块头包括版本号、时间戳、前一个区块的哈希值和当前区块的哈希值。区块体包含交易数据。 创建一个Blockchain类,它…...

Photoscan/Metashape 2.0.0中的地面激光扫描处理
在Metashape(原Photoscan)2.0.0, 结构化地面激光扫描和非结构化航空激光扫描都可以使用导入点云(文件>导入>导入点云)命令导入。导入时会保留所有点属性(包括结构化信息)。 本文讨论以下主题 如何将激光扫描数据导入项目&am…...
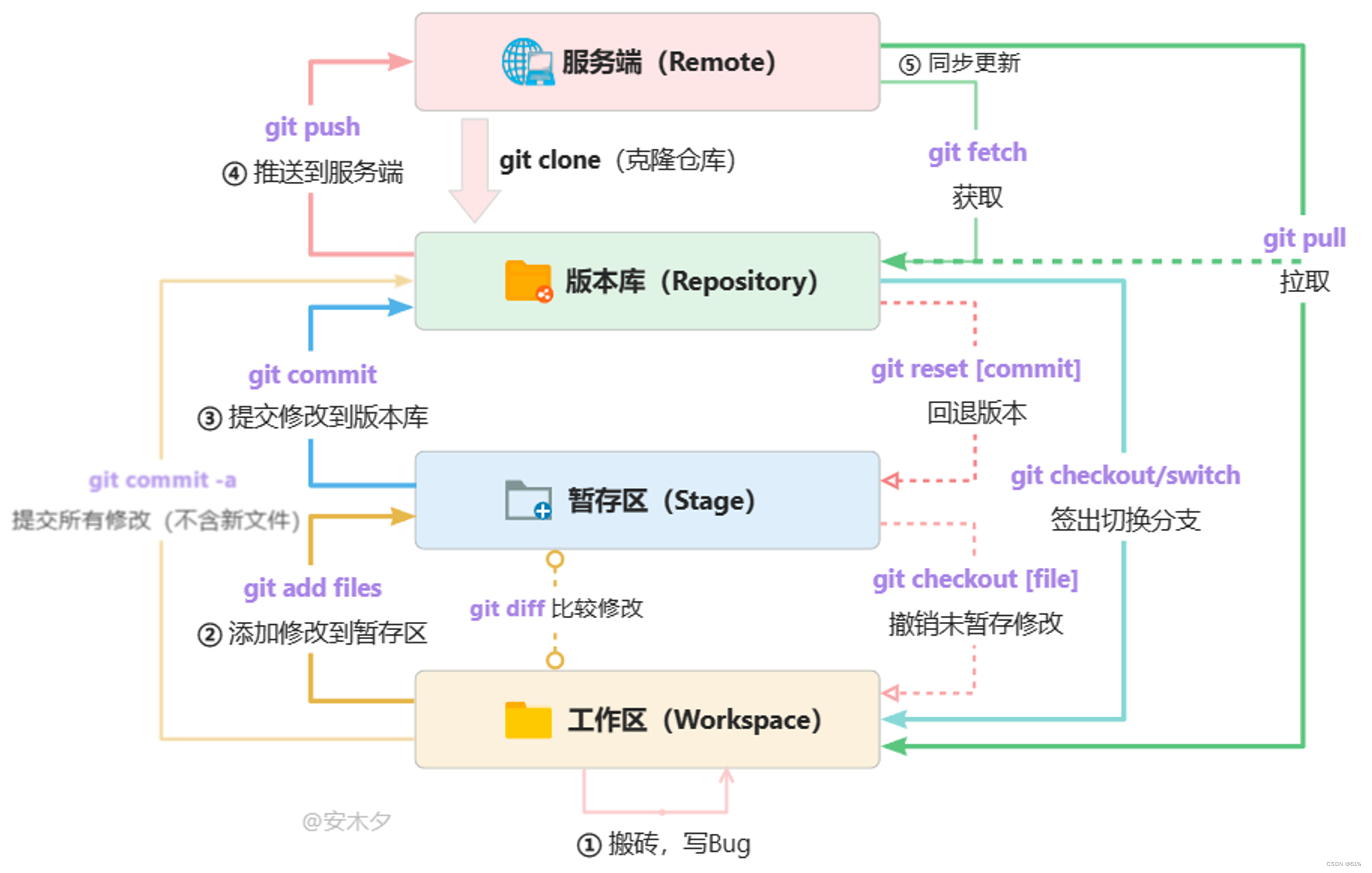
git快速使用
1、下载git 设置签名 2、基本概念 工作区:写代码的地方。 暂存区:.git的.index 工作区:.git 3、常用操作 本地codinggit init, 初始化一个本地仓库,项目根目录下会出现个.gitgit remote add origin gitgithub.com…...

java 实现代理模式
代理模式(Proxy Pattern)是一种结构型设计模式,它允许一个对象(代理对象)充当另一个对象(被代理对象)的接口,以控制对该对象的访问。代理模式通常用于以下情况: 远程代理…...

【每日一题】力扣1768. 交替合并字符串
题目以及链接: 1768. 交替合并字符串 给你两个字符串 word1 和 word2 。请你从 word1 开始,通过交替添加字母来合并字符串。如果一个字符串比另一个字符串长,就将多出来的字母追加到合并后字符串的末尾。 返回 合并后的字符串 。 示例 1&…...
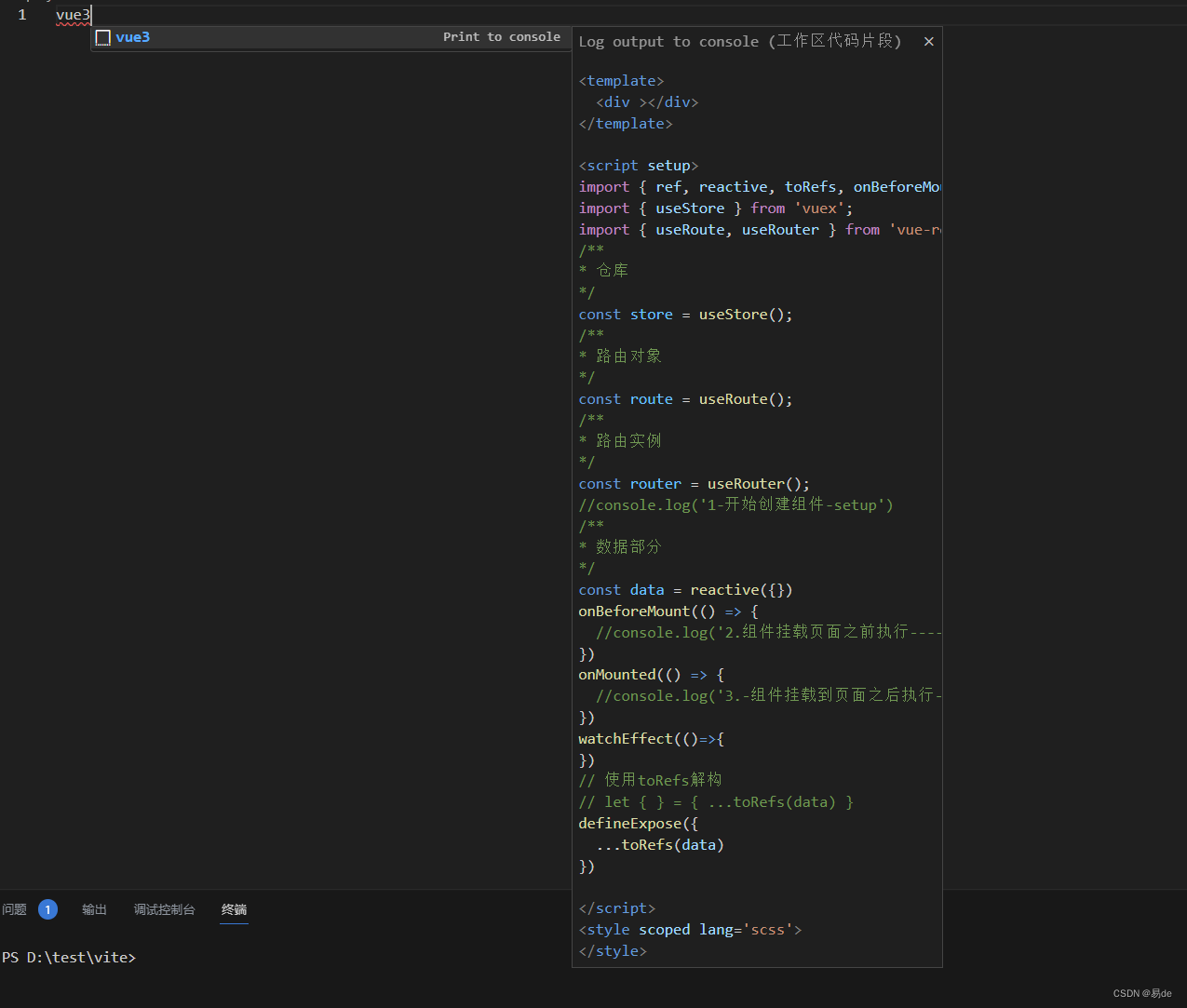
vscode新建vue3文件模板
输入快捷新建的名字 enter 确认后在文件中输入以下内容 {// Place your snippets for vue here. Each snippet is defined under a snippet name and has a prefix, body and// description. The prefix is what is used to trigger the snippet and the body will be expand…...

MySql学习笔记02——MySql的简单介绍
MySQL 常用命令 注意在mysql中使用的命令需要用英文分号结尾(启动/关闭mysql服务不需要带分号) net start mysql 启动mysql服务(需要管理员启动cmd) net stop mysql关闭mysql服务(需要管理员启动cmd) m…...
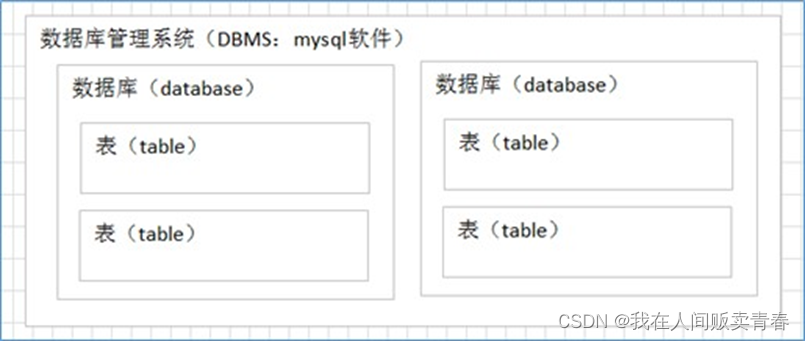
mysql-1:认识mysql
文章目录 数据库概述什么是数据库什么是关系型数据库 MySQL的概述MySQL是什么MySQL发展历程 SQL的概述什么是SQLSQL发展的简要历史:SQL语言分类 数据库概述 什么是数据库 数据库就是[存储数据的仓库],其本质是一个[文件系统],数据按照特定的…...

算法通关村-----堆在查找和排序中的应用
数组中的第K个最大元素 问题描述 给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。详见le…...

直方图统计增强方法
直方图统计增强方法的原理: 直方图统计增强是一种基于像素值分布的图像增强技术,通过调整像素值的分布来增强图像的对比度和细节。其原理是根据图像的直方图信息,将原始像素值映射到一个新的像素值域,从而改变图像的亮度和对比…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...
