Leetcode 1486.数组异或操作

给你两个整数,
n和start。数组
nums定义为:nums[i] = start + 2*i(下标从 0 开始)且n == nums.length。请返回
nums中所有元素按位异或(XOR)后得到的结果。示例 1:
输入:n = 5, start = 0 输出:8 解释:数组 nums 为 [0, 2, 4, 6, 8],其中 (0 ^ 2 ^ 4 ^ 6 ^ 8) = 8 。"^" 为按位异或 XOR 运算符。示例 2:
输入:n = 4, start = 3 输出:8 解释:数组 nums 为 [3, 5, 7, 9],其中 (3 ^ 5 ^ 7 ^ 9) = 8.示例 3:
输入:n = 1, start = 7 输出:7示例 4:
输入:n = 10, start = 5 输出:2提示:
1 <= n <= 10000 <= start <= 1000n == nums.length
我的答案:
一、信息
1.给了我们两个整数 n start
2.num数组中的值由式子 num[]=start+2*i(数组下标)
3.n代表了了该数组的长度
4.要我们返回数组中所有元素并按位 异或(XOR)得到结果
二、步骤
第一步 输入两个整数
第二步 定义个num并给num通过条件2给的公式赋值和用N确定长度
第三步就是返回
三、
四、问题出现
这个有元素按位异或(XOR)后得到的结果是什么意思?
这话的意思就是将数组里的第一个元素和第二个进行异或然后结果和第三个元素异或。
五、实现
Leetcode题解:
方法一:模拟
思路
按照题意模拟即可:
初始化 ans=0\textit{ans} = 0ans=0;
遍历区间 [0,n−1][0, n - 1][0,n−1] 中的每一个整数 iii,令 ans\textit{ans}ans 与每一个 start+2×i\textit{start} + 2 \times istart+2×i 做异或运算;
最终返回 ans\textit{ans}ans,即我们需要的答案。
C++:
class Solution(int x) {
public:int sumXor(int x) {if (x % 4 == 0) {return x;}if (x % 4 == 1) {return 1;}if (x % 4 == 2) {return x + 1;}return 0;}int xorOperation(int n, int start) {int s = start >> 1, e = n & start & 1;int ret = sumXor(s - 1) ^ sumXor(s + n - 1);return ret << 1 | e;}
}方法二 异或法

Leetcode答案:
C++:
class Solution {
public:int sumXor(int x) {if (x % 4 == 0) {return x;}if (x % 4 == 1) {return 1;}if (x % 4 == 2) {return x + 1;}return 0;}int xorOperation(int n, int start) {int s = start >> 1, e = n & start & 1;int ret = sumXor(s - 1) ^ sumXor(s + n - 1);return ret << 1 | e;}
};我的理解:
这个解决方案运用了数学性质和位运算的技巧来减少计算的复杂度。让我们一步一步解析这段代码和它的思考过程。
### 思考过程和分析过程
1. **问题理解**
首先我们需要计算以下数列的异或总和:
\[
\text{start} \oplus (\text{start} + 2) \oplus (\text{start} + 4) \oplus \ldots \oplus (\text{start} + 2(n-1))
\]
2. **性质分析**
在开始编码之前,我们首先注意到异或运算有一些特定的性质,可以用于简化我们的问题:
- 交换律:\(x \oplus y = y \oplus x\)
- 结合律:\((x \oplus y) \oplus z = x \oplus (y \oplus z)\)
- 自反性:\(x \oplus y \oplus y = x\)
- 每四个连续的整数异或结果为0:\(4i \oplus (4i+1) \oplus (4i+2) \oplus (4i+3) = 0\)
3. **简化问题**
通过对数列的分析,我们注意到所有数都有相同的奇偶性。我们可以将所有数除以2(或右移一位),然后最后加上一个修正项来获得最终答案。修正项由start的最低位和n的奇偶性决定。
4. **函数sumXor**
为了解决问题,我们设计了一个函数sumXor(x),它计算从0到x的所有整数的异或和。由于每四个连续的整数异或结果为0,我们可以只考虑x除以4的余数来计算结果。
### 代码演绎和推理
1. **sumXor函数**
这个函数根据输入x的值返回0到x的异或总和。由于每四个连续的整数异或结果为0,函数只需要考虑x除以4的余数来得出结果。
2. **主函数**
主函数计算了s(即start除以2的结果)和e(表示最终结果的最低位,只有当n和start都是奇数时才为1)。然后,它计算了sumXor(s-1)和sumXor(s+n-1)的异或值,然后将结果乘以2并添加e来获得最终结果。
### 检查答案的过程
为了检查我们的答案,我们可以使用一些示例输入来运行我们的代码,并验证输出是否与预期匹配。如果所有测试都通过,我们可以有信心我们的解决方案是正确的。
现在,我们可以使用这个方法来实现C,C++和Java版本的解决方案。
总结:
从这个题目中,我们可以学习以下几个方面:
1. **高效算法的设计**:不是所有的问题都需要通过直接的方式解决。在这种情况下,直接计算数组的所有元素的异或将会花费较多的时间(O(n)时间复杂度)。但是通过运用数学技巧,我们可以将时间复杂度降到O(1)。
2. **异或运算的性质和应用**:这个题目深刻地展示了异或运算的一些基本性质,如交换律、结合律和自反性。同时,题目也介绍了一个特定的性质,即连续4个整数的异或结果为0。
3. **位运算的应用**:这个题目用到了位运算的一些技巧,包括右移运算来实现除以2和用位运算来检查奇偶性。位运算是一种高效的计算方式,通常比算术运算更快。
4. **问题简化技巧**:这个题目展示了如何通过简化问题来找到一个更高效的解决方案。在这种情况下,我们通过将问题简化为求解一个更小范围的异或和,然后通过数学技巧得到了答案。
5. **函数的应用**:通过创建`sumXor`函数来计算一个范围内的异或和,我们能够使代码更清晰和模块化,这也使得解决方案更易于理解和实现。
6. **数学归纳与分析**:解决这个问题需要深入的数学分析和推理,展示了数学在算法设计和分析中的重要性。
7. **测试和验证**:最后,我们可以通过创建测试案例来验证我们的解决方案。这不仅可以帮助我们验证我们的解决方案是否正确,而且还可以帮助我们更好地理解问题和解决方案的工作原理。
综上所述,这个题目是一个很好的示例,展示了如何通过数学技巧和算法设计技术来解决一个看似复杂的问题。
从这道题中,我们可以学到以下几点新的思想、方法和思维:
1. **抽象化和一般化**:
- 学习如何从具体的情境中提取一般性的原理或模式,这有助于我们形成更高效的解决策略。
2. **分而治之的思想**:
- 问题被分解为几个更小的部分,分别解决,然后合并结果。这在算法设计中是一个非常有用和强大的策略。
3. **数学与编程的结合**:
- 这道题目深刻体现了数学和编程的交叉应用。在编程中引入数学分析可以更好地优化解决方案。
4. **递归思想的应用**:
- 通过创建一个计算异或和的函数,我们可以看到递归思想的影子。这种思想可以帮助我们在解决问题时更好地组织代码和逻辑。
5. **空间复杂度的降低**:
- 通过数学方法我们避免了明显的数组分配和迭代,从而降低了空间复杂度。
6. **利用已有规律简化问题**:
- 观察并利用已知的规律或性质(例如,连续四个数的异或为0)可以大大简化问题和解决方案。
7. **边界情况的处理**:
- 在处理问题时,我们需要考虑和处理边界情况,这是算法设计中一个非常重要的步骤。
8. **代码的模块化**:
- 通过将复杂问题分解成更小的函数或模块,可以使代码更清晰和易于维护。
通过学习和理解这种类型的问题和解决方案,我们可以培养更深层次的问题解决能力和思维方式,这将有助于我们在未来遇到类似或更复杂问题时更有效地解决它们。

相关文章:

Leetcode 1486.数组异或操作
给你两个整数,n 和 start 。 数组 nums 定义为:nums[i] start 2*i(下标从 0 开始)且 n nums.length 。 请返回 nums 中所有元素按位异或(XOR)后得到的结果。 示例 1: 输入:n 5, …...

【Java】Java核心API概述
Java核心API是Java编程语言的基础,包含了Java应用程序中常用的类和接口。本文将介绍Java核心API中的一些重要部分,包括输入输出流、异常处理、集合框架、多线程和网络编程等。 1、输入输出流 Java的输入输出流API是Java IO,它提供了处理输入…...

微信小程序检查版本更新
新建文件 version-util.js // 小程序启动时检查版本 class VersionUtil {/*** 检查更新*/checkUpdate(){const updateManager wx.getUpdateManager();updateManager.onCheckForUpdate((hasUpdate)>{if(hasUpdate){updateManager.onUpdateReady(()>{wx.showModal({title…...
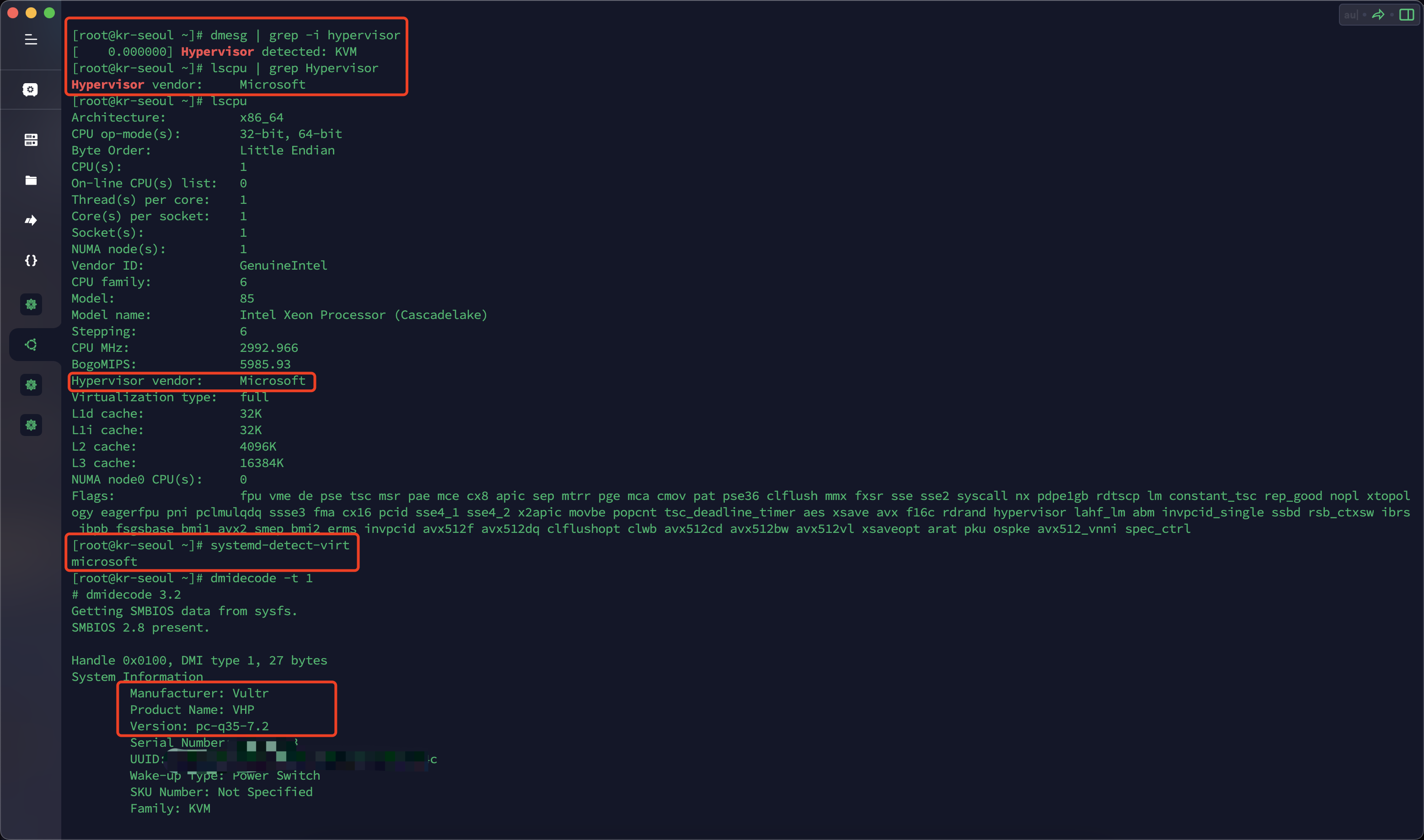
Linux查看是虚拟机还是物理机
第一种方式:dmesg命令 [roottest ~]# dmesg | grep -i hypervisor [ 0.000000] Hypervisor detected: VMware [ 0.001000] TSC freq read from hypervisor : 2903.999 MHz [ 6.311621] [drm] Max dedicated hypervisor surface memory is 0 kiB第二种方式…...
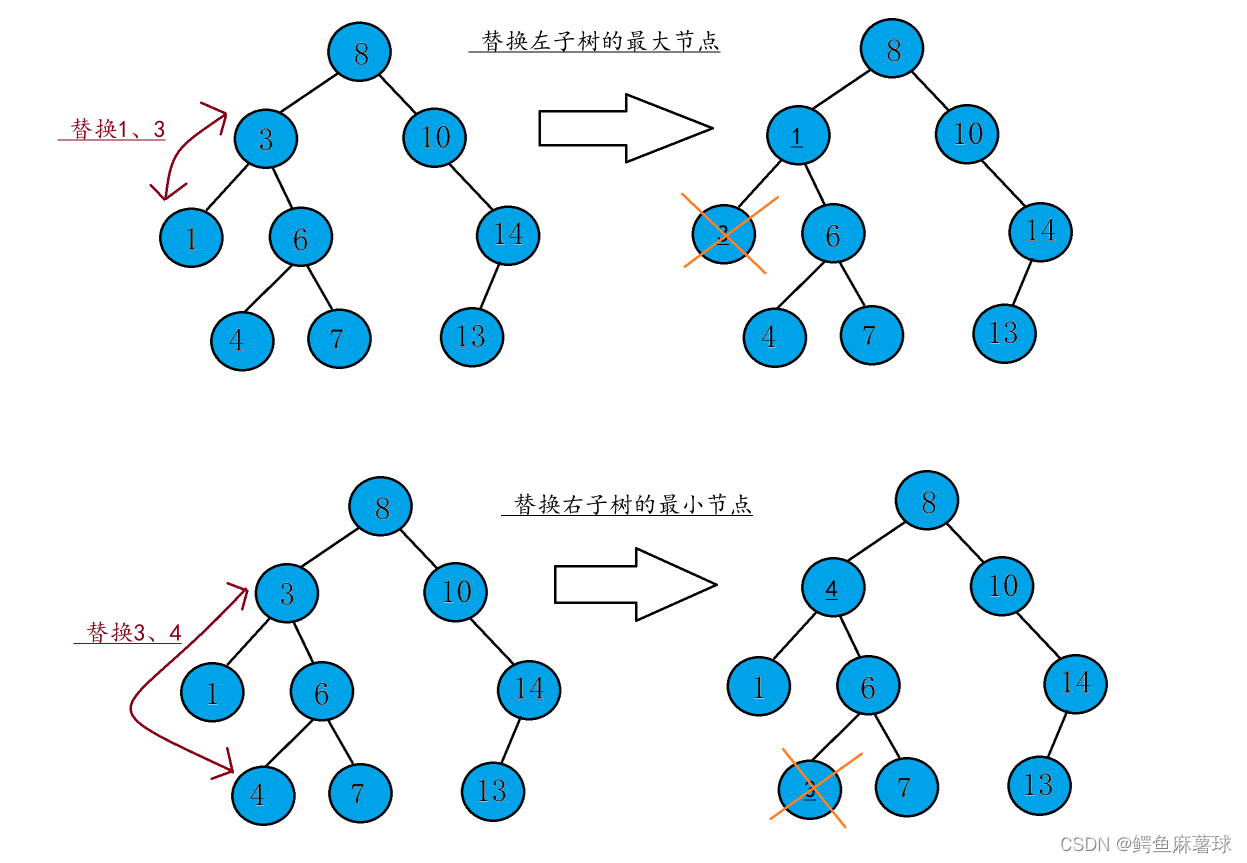
【数据结构】二叉搜索树——二叉搜索树的概念和介绍、二叉搜索树的简单实现、二叉搜索树的增删查改
文章目录 二叉搜索树1. 二叉搜索树的概念和介绍2. 二叉搜索树的简单实现2.1二叉搜索树的插入2.2二叉搜索树的查找2.3二叉搜索树的遍历2.4二叉搜索树的删除2.5完整代码和测试 二叉搜索树 1. 二叉搜索树的概念和介绍 二叉搜索树又称二叉排序树,它或者是一棵空树&…...

通过linux定时任务删除es日志索引
能过linux定时任务删除es日志索引 项目用上了elk,产生的日志索引要定时,其一个方法,通过linux定时任务,调用es接口删除索引。 #!/bin/bash #删除ELK30天前的日志 #计算索引名称包含的日期,比如这里是 %Y.%m.%d (2023…...

【跟小嘉学 Rust 编程】二十二、常用 API
系列文章目录 【跟小嘉学 Rust 编程】一、Rust 编程基础 【跟小嘉学 Rust 编程】二、Rust 包管理工具使用 【跟小嘉学 Rust 编程】三、Rust 的基本程序概念 【跟小嘉学 Rust 编程】四、理解 Rust 的所有权概念 【跟小嘉学 Rust 编程】五、使用结构体关联结构化数据 【跟小嘉学…...

【ES6】Class中this指向
先上代码: 正常运行的代码: class Logger{printName(name kexuexiong){this.print(hello ${name});}print(text){console.log(text);} }const logger new Logger(); logger.printName("kexueixong xiong");输出: 单独调用函数p…...

Python 编程竟然如此幽默!揭秘程序员们的搞笑日常,快来看看吧!
食用原文效果更佳,原文链接 Python 编程竟然如此幽默!揭秘程序员们的搞笑日常,快来看看吧! 在 Python 编程的世界里,充满了智慧与创造力。 当然,也少不了轻松幽默的段子,这些段子让程序员们在…...
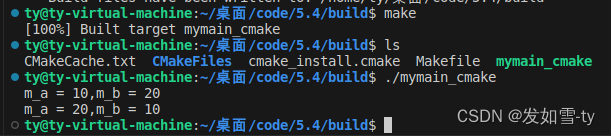
Linux c++开发-03-使用CMake组织工程
一、简单文件的编译 有如下的目录结构: 其中 helloworld.cpp如下: #include <iostream> using namespace std; int main() {printf("hello world my name is Ty!");return 0; }CMakeLists.txt如下: cmake_minimum_requir…...
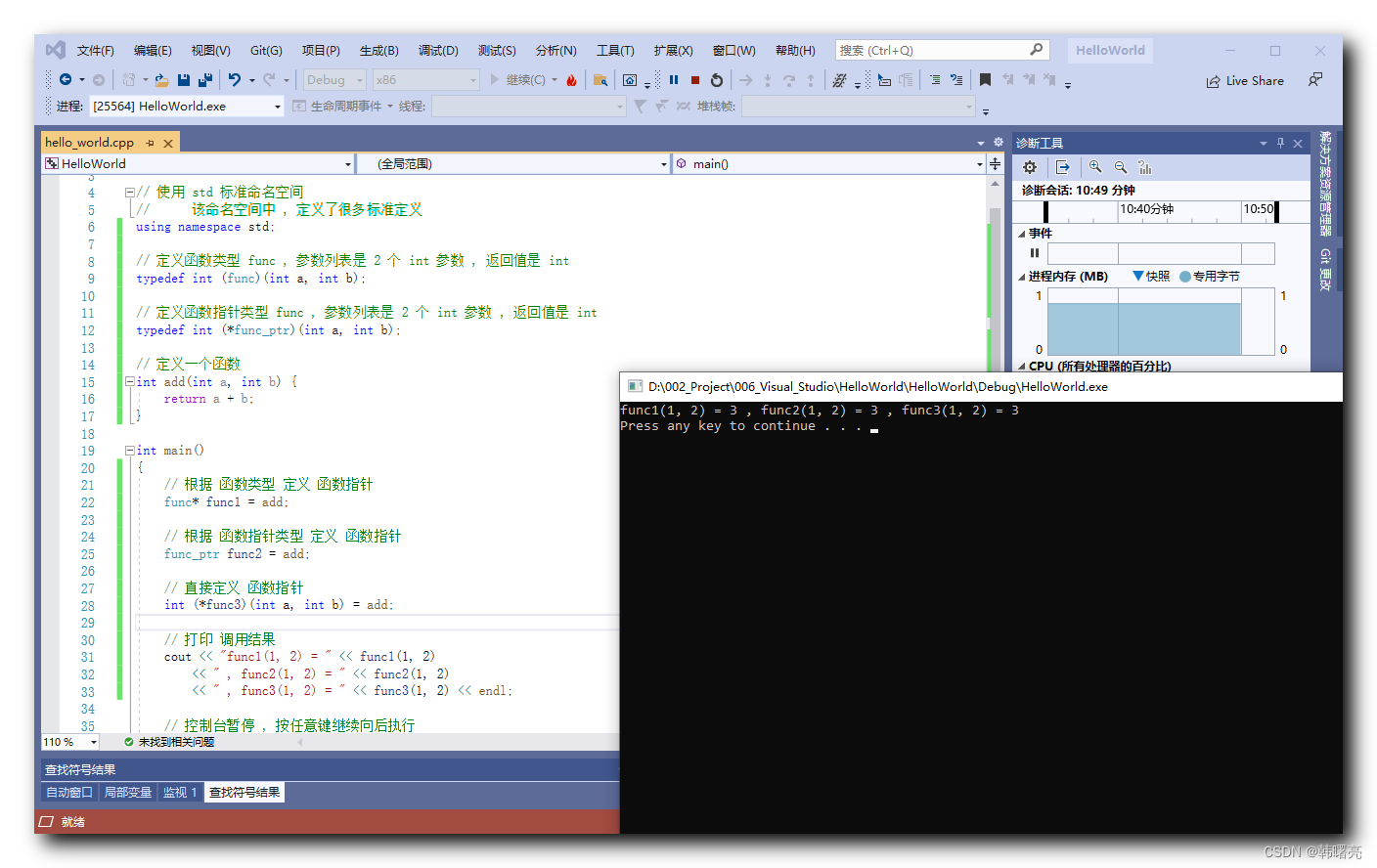
【C++】函数重载 ④ ( 函数指针定义的三种方式 | 直接定义函数指针 | 通过 函数类型 定义 函数指针 | 通过 函数指针类型 定义 函数指针 )
文章目录 一、函数指针定义方法1、直接定义函数指针2、通过 函数类型 定义 函数指针3、通过 函数指针类型 定义 函数指针4、代码示例 - 不同方式定义函数指针 博客总结 : 重载函数 : 使用 相同 的 函数名 , 定义 不同 的 函数参数列表 ;判定标准 : 只有 函数参数 的 个数 / 类…...
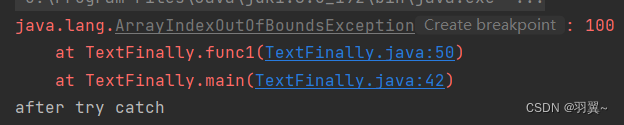
异常-java
目录 一、异常的概念和体系结构 1.1 异常的概念 1.2 异常的体系结构 1.3 异常的分类 二、异常的处理 2.1 防御式编程 2.2 异常抛出 2.3 异常捕获 2.4 异常处理流程 三、自定义异常类 一、异常的概念和体系结构 1.1 异常的概念 程序员在开发过程中,想要将代码写得…...

软件测试/测试开发丨Selenium Web自动化测试 高级控件交互方法
点此获取更多相关资料 本文为霍格沃兹测试开发学社学员学习笔记分享 原文链接:https://ceshiren.com/t/topic/27045 一、使用场景 使用场景对应事件复制粘贴键盘事件拖动元素到某个位置鼠标事件鼠标悬停鼠标事件滚动到某个元素滚动事件使用触控笔点击触控笔事件&am…...

深入Go语言:进阶指南
深入Go语言:进阶指南 欢迎来到深入Go语言的进阶指南。如果你已经熟悉Go语言的基础知识,想要更深入地探索这门语言的高级特性和技巧,那么本篇博客将为你提供有关Go语言的更多深入内容。 Go语言的并发编程 Go语言以其强大的并发支持而闻名。…...

FOXBORO FBM232 P0926GW 自动化控制模块
Foxboro FBM232 P0926GW 是 Foxboro(福克斯博罗)自动化控制系统的一部分,通常用于监测和控制工业过程。以下是关于这种类型的自动化控制模块可能具有的一些常见功能: 数字输入通道: FBM232 P0926GW 控制模块通常具有多…...

【C# Programming】编程入门:方法和参数
一、方法 1、方法的定义 由一系列以执行特定的操作或计算结果语句组成。方法总是和类关联,类型将相关的方法分为一组。 方法名称 形参和实参(parameter & argument)返回值 2、命名空间 一种分类机制,用于组合功能相关的所有类型。命名空间是分级…...
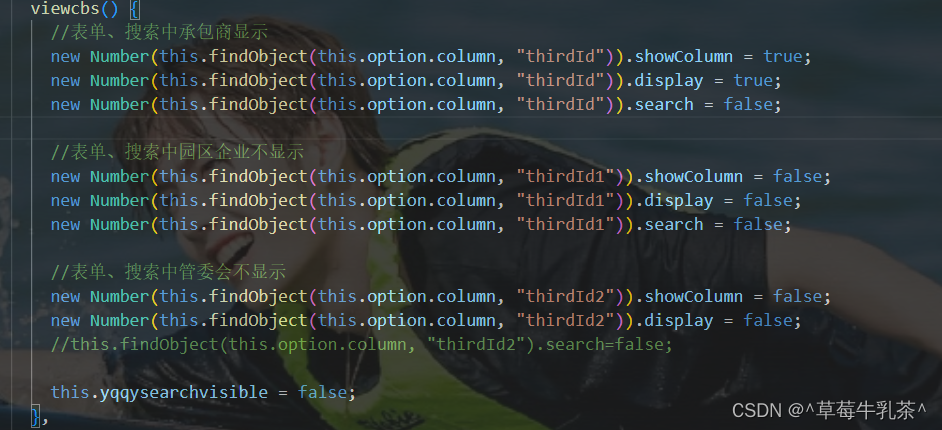
【报错】 Cannot create property ‘showColumn‘ on number ‘-1‘
1、报错原因: 代码如下: 报错是因为:this.findObject(this.option.column, "thirdId")是一个number ,没有.showColumn属性 2、修改代码 将其变成object属性就行了...

C++容器string的运用和注意
介绍 首先,先说明,string在C的string头文件中定义,而在C语言中的字符串就是字符数组,在C中,string容器相当于C语言中的字符数组,string比C语言中的字符数组更为好用,如:C中cin/cout可…...
用对工具,你的全渠道电子商务业务就成功了一半
希望将全渠道电子商务纳入您的业务战略,但不确定从哪里开始?我们为您提供保障。这篇文章将指导您了解全渠道商务的基础知识,以及它与多渠道方法的区别,还将探讨利用全渠道方法的众多好处,并讨论企业如何通过全渠道客户…...
:采集量(Metric),标签(label),数据采集点,表,超级表,子表、库)
TDengine学习(1):采集量(Metric),标签(label),数据采集点,表,超级表,子表、库
因为TDengine是面向物联网诞生的一种数据库,所以在一些概念的命名上有一点相应的特色。 一、数据采集点 比如需要对一辆高铁上的各种信息进行采集,采集信息存入数据库中。我们可以对高铁车厢内的一些数据进行采集,比如:车厢内温…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

MyBatis中关于缓存的理解
MyBatis缓存 MyBatis系统当中默认定义两级缓存:一级缓存、二级缓存 默认情况下,只有一级缓存开启(sqlSession级别的缓存)二级缓存需要手动开启配置,需要局域namespace级别的缓存 一级缓存(本地缓存&#…...

如何配置一个sql server使得其它用户可以通过excel odbc获取数据
要让其他用户通过 Excel 使用 ODBC 连接到 SQL Server 获取数据,你需要完成以下配置步骤: ✅ 一、在 SQL Server 端配置(服务器设置) 1. 启用 TCP/IP 协议 打开 “SQL Server 配置管理器”。导航到:SQL Server 网络配…...
