灰度变换与空间滤波
灰度变换与空间滤波
背景知识
- 空间域指包含图像像素的平面,灰度变换与空间滤波均在空间域进行,即直接在图像像素上操作,表示为 g ( x , y ) = T [ f ( x , y ) ] g(x,y)=T[f(x,y)] g(x,y)=T[f(x,y)] ,其中 T T T 是在点 ( x , y ) (x, y) (x,y) 的邻域上定义的关于 f f f 的一种算子
- 如空间滤波:邻域与预定义的操作共称为空间滤波器(也称为空间掩膜、核、模版或窗口)
- 空间滤波的最小邻域为 1 × 1 1\times1 1×1 ,此时 T T T 成为灰度变换函数: s = T ( r ) s=T(r) s=T(r) ,可以起到对比度拉伸或阈值处理的作用
- 图像增强应用
- 增强是指对图像进行加工,使其结果对于特定的应用比原始图像更适合的一种处理
灰度变换函数

-
图像反转
- s = L − 1 − r s=L-1-r s=L−1−r
- 适用于增强嵌入在一幅图像的暗区域中的白色或灰色细节,特别当黑色面积在尺寸上站主导地位时
-
对数变换
- s = c l o g ( 1 + r ) s=clog(1+r) s=clog(1+r)
- 该变换将输入中范围较窄的低灰度值映射为输出中较宽范围的灰度值;对高的输入灰度值起相反作用
- 使用对数变换来扩展图像中暗像素的值,同时压缩更高灰度级的值
- 反对数变换与对数变换相反
- 对数变换可以压缩像素值变化较大的图像的动态范围,比如傅立叶频谱。傅立叶频谱的范围一般在 0 ∼ 1 0 6 0\sim10^6 0∼106 ,通过对数变换后可以显示图像中丰富的细节
-
幂律(伽马)变换

- s = c r γ s=cr^\gamma s=crγ
- 随着 γ \gamma γ 的变化,得到一族可能的变换曲线(分界点为 γ = 1 \gamma = 1 γ=1 ,此时简化成了恒等变换)
- 用于图像获取、显示、打印的各种设备常根据幂律来产生相应,因此应用伽马矫正来矫正这些幂律响应现象
- 幂律变换同样可用于调整图像的对比度:当 γ < 1 \gamma\lt1 γ<1 时,减小对比度;当 γ > 1 \gamma\gt1 γ>1 时,增加对比度
-
分段线性变换函数

-
对比度拉伸:一般函数是单值且单调递增的,保持了灰度级的次序(包括了阈值处理函数)
-
灰度级分层:用于突出图像特定灰度范围的亮度

- 一种方法将感兴趣范围内所有灰度显示为一个值,将其他灰度值显示为另一个值
- 另一种方法使感兴趣范围的灰度变亮(或变暗),而保持图像中的其他灰度级不变
-
比特平面分层:将 256 级灰度图像分成 8 个 1 比特平面来表示,通过阈值灰度变换函数处理来得到对应平面的二值图像

- 可用于图像压缩:通过特定几个平面来恢复图像
-
直方图处理
- 直方图定义: p ( r k ) = n k M N p(r_k)=\frac{n_k}{MN} p(rk)=MNnk (类比概率)
- 直方图均衡
- 灰度映射: s = T ( r ) s=T(r) s=T(r)
- T ( r ) T(r) T(r) 在区间 0 ≤ r ≤ L − 1 0\leq r\leq L-1 0≤r≤L−1 上为(严格)单调递增函数
- 当 0 ≤ r ≤ L − 1 0\leq r\leq L-1 0≤r≤L−1 时, 0 ≤ T ( r ) ≤ L − 1 0\leq T(r)\leq L-1 0≤T(r)≤L−1
- 重要变换函数: s = T ( r ) = ( L − 1 ) ∫ 0 r p r ( w ) d w s=T(r)=(L-1)\int^r_0p_r(w)dw s=T(r)=(L−1)∫0rpr(w)dw
- 离散形式: s k = T ( r k ) = ( L − 1 ) ∑ j = 0 k p r ( r j ) = ( L − 1 ) M N ∑ j = 0 k n j , k = 0 , 1 , 2 , . . . , L − 1 s_k=T(r_k)=(L-1)\sum^k_{j=0}p_r(r_j)=\frac{(L-1)}{MN}\sum^k_{j=0}n_j,\ k=0, 1, 2, ...,L-1 sk=T(rk)=(L−1)∑j=0kpr(rj)=MN(L−1)∑j=0knj, k=0,1,2,...,L−1
- 对于该变换函数,恒有 p s ( s ) = p r ( r ) ∣ d r d s ∣ = p r ( r ) ∣ 1 ( L − a ) p r ( r ) ∣ = 1 L − 1 p_s(s)=p_r(r)|\frac{dr}{ds}|=p_r(r)|\frac{1}{(L-a)p_r(r)}|=\frac{1}{L-1} ps(s)=pr(r)∣dsdr∣=pr(r)∣(L−a)pr(r)1∣=L−11 ,即 p s ( s ) p_s(s) ps(s) 始终是均匀的,与 p r ( r ) p_r(r) pr(r) 的形式无关
- 只要图像直方图中没有为 0 的分量,就满足严格单调递增,可以进行反变换 r k = T − 1 ( s k ) r_k=T^{-1}(s_k) rk=T−1(sk)
- 局部直方图均衡,自适应直方图均衡
- 参考资料
- 灰度映射: s = T ( r ) s=T(r) s=T(r)
- 直方图匹配
- 直方图匹配(规范化)用于在处理后产生特殊直方图
- 步骤
1. 由输入图像得到 p r ( r ) p_r(r) pr(r) ,并通过直方图均衡得到 s s s 的值
2. 通过 G ( z ) = ( L − 1 ) ∫ 0 z p z ( t ) d t = s G(z)=(L-1)\int^z_0p_z(t)dt=s G(z)=(L−1)∫0zpz(t)dt=s 中指定的 p z ( z ) p_z(z) pz(z) 求得变换函数 G ( z ) G(z) G(z) ;对于离散函数,用 G ( z q ) = ( L − a ) ∑ i = 0 q p z ( z i ) G(z_q)=(L-a)\sum^q_{i=0}p_z(z_i) G(zq)=(L−a)∑i=0qpz(zi) 对 q = 0 , 1 , . . . , L − 1 q=0,1,...,L-1 q=0,1,...,L−1 计算变换函数 G G G 的所有值,将其四舍五入为范围 [ 0 , L − 1 ] [0,L-1] [0,L−1] 内的整数,存入一个表中
3. 求得反变换函数 = G − 1 ( z ) =G^{-1}(z) =G−1(z) ;对于离散函数,对每一个值 s k s_k sk 找到对应的 z q z_q zq 值,以使 G ( z q ) G(z_q) G(zq) 最接近 s k s_k sk ,并储存这些从 s s s 到 k k k 的映射,当映射不唯一时,按惯例选择最小的值
4. 对经过直方图均衡的图像中每个像素执行反变换函数,最后输出图像的 PDF 将等于指定的 PDF;对于离散函数,使用上一步找到的映射把该图像每个均衡后的像素值 s k s_k sk 映射为直方图规定化后的图像中相应的 z q z_q zq 值,形成直方图规范化后的图像
- 在图像增强中使用直方图统计
- 平均灰度、灰度方差
- 局部均值、局部方差:与全局均值、方差做比较来判断当前区域的亮度和对比度特征
空间滤波基础
- 滤波一词一般用于频域处理中,指接受或拒绝一定的频率分量;而空间滤波器也可以直接作用于图像本身
- 空间滤波机理
- 空间滤波器由一个邻域(一般为较小矩形)和对该邻域包围的像像素执行的预定义操作组成。根据操作的不同,可以分为线性滤波器和非线性滤波器
- 空间相关与卷积
- 相关
- w ( x , y ) ⋆ f ( x , y ) = ∑ s = − a a ∑ t = − b b w ( s , t ) f ( x + s , y + t ) w(x,y)\star f(x,y)=\sum^a_{s=-a}\sum^b_{t=-b}w(s,t)f(x+s,y+t) w(x,y)⋆f(x,y)=∑s=−aa∑t=−bbw(s,t)f(x+s,y+t)
- 相关是滤波器模版移过图像并计算每个位置乘积之和的处理,是滤波器位移的函数
- 一个函数与离散单位冲激相关,在该冲激位置产生这个函数一个翻转的版本
- 卷积
- w ( x , y ) ⋆ f ( x , y ) = ∑ s = − a a ∑ t = − b b w ( s , t ) f ( x − s , y − t ) w(x,y)\star f(x,y)=\sum^a_{s=-a}\sum^b_{t=-b}w(s,t)f(x-s,y-t) w(x,y)⋆f(x,y)=∑s=−aa∑t=−bbw(s,t)f(x−s,y−t)
- 卷积的机理与相关类似,只不过滤波器要先旋转 18 0 ∘ 180^{\circ} 180∘
- 卷积的特性是某个函数与某个单位冲激卷积,得到一个在该冲激处的这个函数的拷贝
- 如果滤波器模版是对称的,相关和卷积将得到同样的结果
- 相关
- 线性滤波的向量表示: R = w 1 z 1 + w 2 z 2 + . . . + w m n z m n = ∑ k = 1 m n = w T z R=w_1z_1+w_2z_2+...+w_{mn}z_{mn}=\sum^{mn}_{k=1}=\mathbf{w^Tz} R=w1z1+w2z2+...+wmnzmn=∑k=1mn=wTz
- 空间滤波器模版的产生
- 滤波器模版的系数由进行的操作来决定,需注意线性滤波仅能实现乘积求和操作;而非线性滤波要求确定邻域的大小,以及对包含在邻域内图像像素执行的操作
平滑空间滤波器
- 平滑滤波器常用于模糊处理与降低噪声(预处理任务中)
- 平滑线性滤波
- 平滑线性空间滤波器的输出是包含在滤波器模版邻域内的像素的简单平均值 w i = 1 m n w_i=\frac{1}{mn} wi=mn1 ,也称为均值滤波器
- 平滑滤波器可以降低图像灰度的尖锐变化,而典型的随机噪声和图像边缘均由灰度的尖锐变化导致
- 还可以使用加权平均模版,即给不同像素不同的权重
- 空间均值处理的一个重要应用就是为了对感兴趣的物体得到一个粗略的描述模糊一幅图像,这样较小物体的灰度就与背景混合在一起,而较大物体变得像斑点而易于检测
- 统计排序(非线性)滤波器
- 统计排序滤波器的响应以滤波器包围的图像区域中所包含的像素的排序为基础,然后使用统计排序的结果所决定的值替代中心像素的值
- 中值滤波器:将像素邻域内灰度的中值代替该像素的值
- 对于脉冲噪声(椒盐噪声)非常有效,且比现行平滑滤波器的模糊程度要低
- 主要功能是使拥有不同灰度的点看起来更接近于他的相邻点
- 最大滤波器、最小滤波器
锐化空间滤波器
- 锐化处理的主要目的是突出灰度的过渡部分
- 图像模糊可通过在空间域用像素邻域平均法实现,因为均值处理与积分类似;而锐化处理可由空间微分来实现,因为微分算子的相应强度与图像在用算子操作的这一点的突变程度成正比
- 一阶微分: ∂ f ∂ x = f ( x + 1 ) − f ( x ) \frac{\partial f}{\partial x}=f(x+1)-f(x) ∂x∂f=f(x+1)−f(x)
- 二阶微分: ∂ 2 f ∂ x 2 = f ( x + 1 ) + f ( x − 1 ) − 2 f ( x ) \frac{\partial^2f}{\partial x^2}=f(x+1)+f(x-1)-2f(x) ∂x2∂2f=f(x+1)+f(x−1)−2f(x)

- 图像的一阶微分常常在灰度变化处产生较粗的边缘,而二阶微分由零产生分开的双边缘;同时,在图像灰度陡变处,二阶微分将产生零交叉,对于边缘定位十分有用。因此,二阶微分在增强细节方面要比一阶微分好得多,是一个适合锐化图像的理想特性
- 二阶微分:拉普拉斯算子
- 拉普拉斯算子是最简单的各向同性微分算子(线性)
- ∇ 2 f = ∂ 2 f ∂ x 2 + ∂ 2 f ∂ y 2 = f ( x + 1 , y ) + f ( x − 1 , y ) + f ( x , y + 1 ) + f ( x , y − 1 ) − 4 f ( x , y ) \nabla^2f=\frac{\partial^2f}{\partial x^2}+\frac{\partial^2f}{\partial y^2}=f(x+1,y)+f(x-1,y)+f(x,y+1)+f(x,y-1)-4f(x,y) ∇2f=∂x2∂2f+∂y2∂2f=f(x+1,y)+f(x−1,y)+f(x,y+1)+f(x,y−1)−4f(x,y)
- 以上算子仅对 9 0 ∘ 90^\circ 90∘ 为增量旋转的各向同性,若加入沿对角线方向的两项,便可对 4 5 ∘ 45^\circ 45∘ 增幅的结果也为各向同性
- 使用拉普拉斯算子对图像增强: g ( x , y ) = f ( x , y ) + c [ ∇ 2 f ( x , y ) ] g(x,y)=f(x,y)+c[\nabla^2f(x,y)] g(x,y)=f(x,y)+c[∇2f(x,y)]
- 非锐化掩蔽和高提升滤波
- 非锐化掩蔽步骤:
1. 模糊原图像
2. 从原图像中减去模糊图像(产生的差值图像称为模版)
3. 将模版加到原图像上 - g m a s k ( x , y ) = f ( x , y ) − f ˉ ( x , y ) g_{mask}(x,y)=f(x,y)-\bar{f}(x,y) gmask(x,y)=f(x,y)−fˉ(x,y)
g ( x , y ) = f ( x , y ) + k ∗ g m a s k ( x , y ) g(x,y)=f(x,y)+k*g_{mask}(x,y) g(x,y)=f(x,y)+k∗gmask(x,y) - k k k 称为权重系数,当 k = 1 k=1 k=1 时,为非锐化掩蔽;当 k > 1 k\gt1 k>1 时,该处理为高提升滤波
- 如果 k k k 过于大时,可能导致模版峰值大于原信号中的最小值,从而产生负灰度,导致边缘周围由暗的晕轮
- 非锐化掩蔽步骤:
- 一阶微分:梯度
-
梯度的幅值(梯度图像): M ( x , y ) = m a g ( ∇ f ) = g x 2 + g y 2 M(x,y)=mag(\nabla f)=\sqrt {g^2_x+g^2_y} M(x,y)=mag(∇f)=gx2+gy2
- 非线性算子、非各向同性
-
用绝对值来近似平方根更适合计算: M ( x , y ) ≈ ∣ g x ∣ + ∣ g y ∣ M(x,y)\approx |g_x|+|g_y| M(x,y)≈∣gx∣+∣gy∣
-
罗伯特交叉梯度算子
-
Soble 算子,Robert 算子,Prewitt 算子,Kirsch 算子
-
所有模版中系数总和为 0,正如微分算子的期望值,表明灰度恒定区域的相应为 0
-
混合空间增强法
- 使用拉普拉斯法突出图像中的小细节,但是也会增加图像噪声
- 使用梯度法突出图像中的边缘
- 平滑过的梯度图像将用于掩蔽拉普拉斯图像
- 使用灰度变换来增大图像的灰度动态范围
使用模糊技术进行灰度变换和空间滤波
- 模糊逻辑、模糊集合、隶属度函数
- 模糊集合是一个由 z z z 值和相应隶属度函数组成的序对: A = { z , μ A ( z ) ∣ z ∈ Z } A=\{z,\mu_A(z)|z\in Z\} A={z,μA(z)∣z∈Z}
相关文章:

灰度变换与空间滤波
灰度变换与空间滤波 背景知识 空间域指包含图像像素的平面,灰度变换与空间滤波均在空间域进行,即直接在图像像素上操作,表示为 g ( x , y ) T [ f ( x , y ) ] g(x,y)T[f(x,y)] g(x,y)T[f(x,y)] ,其中 T T T 是在点 ( x , y…...
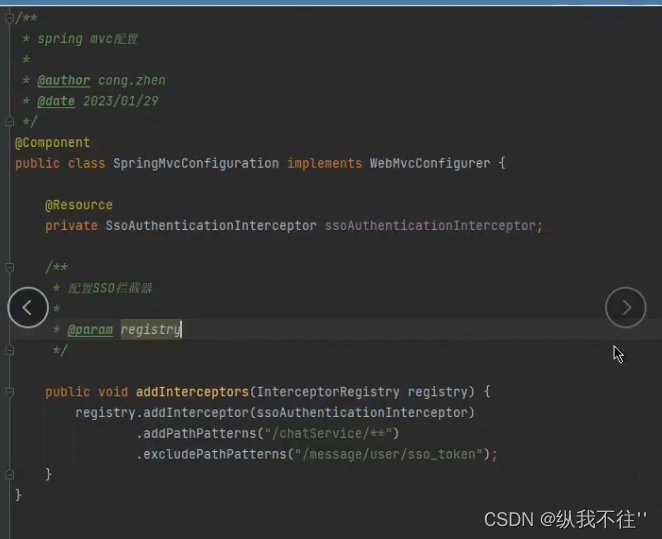
敏感接口权限校验
前端校验 (从前端或者从token里面拿一下),看一下用户有没有这个页面的权限(但是一般不用,因为nodejs也可以写后端,但是放到前端去校验不安全) 后端校验 需要梳理敏感数据接口,将这…...
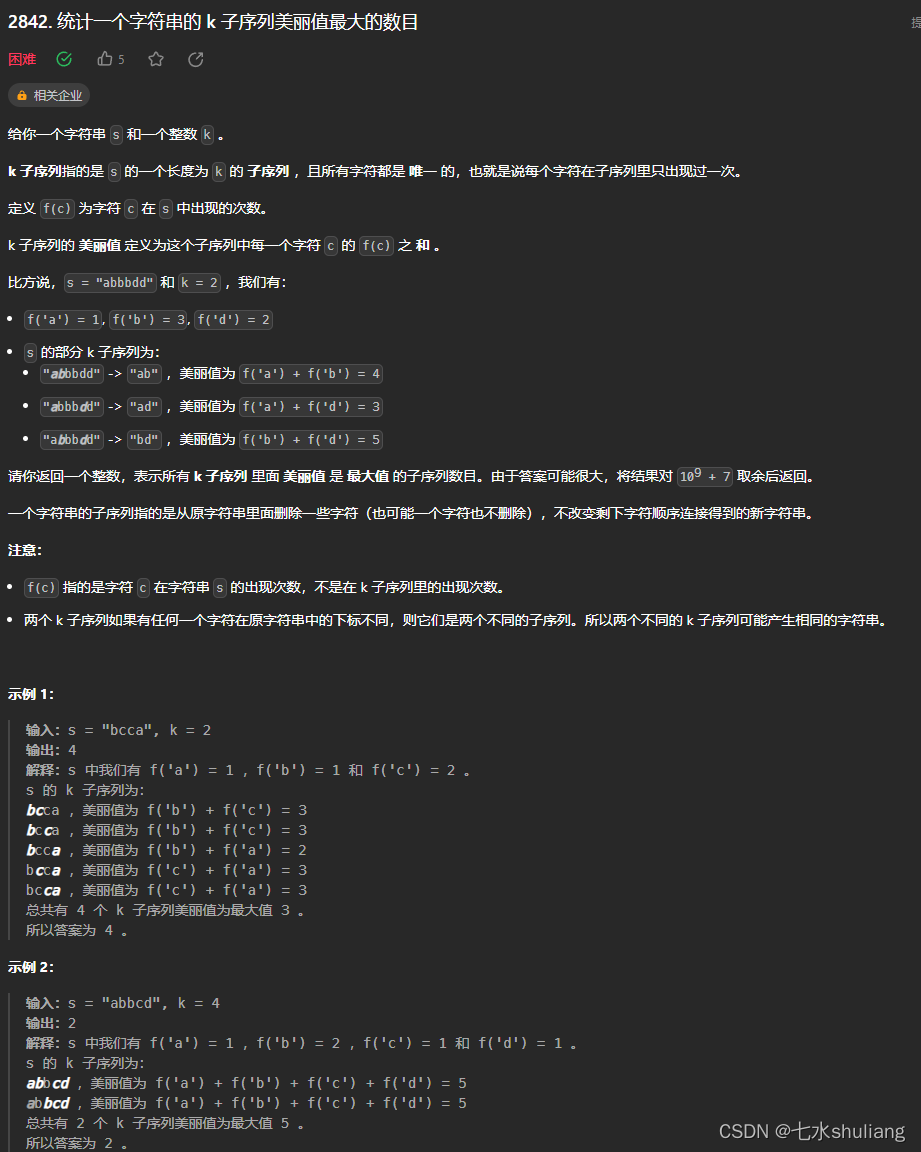
[LeetCode周赛复盘] 第 112场双周赛20230903
[LeetCode周赛复盘] 第 112场双周赛20230903 一、本周周赛总结2839. 判断通过操作能否让字符串相等 I1. 题目描述2. 思路分析3. 代码实现 2840. 判断通过操作能否让字符串相等 II1. 题目描述2. 思路分析3. 代码实现 2841. 几乎唯一子数组的最大和1. 题目描述2. 思路分析3. 代码…...
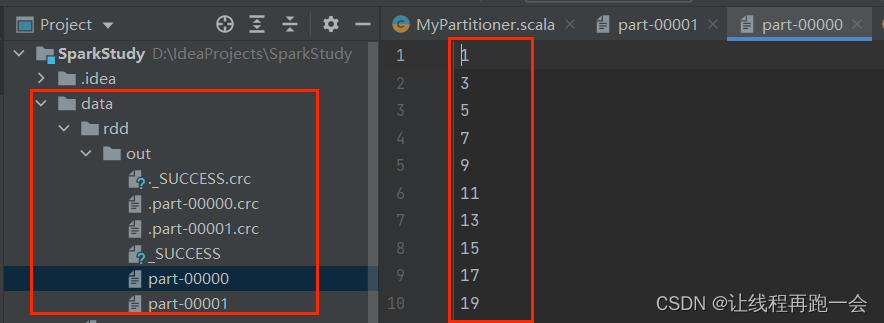
Spark【RDD编程(二)RDD编程基础】
前言 接上午的那一篇,下午我们学习剩下的RDD编程,RDD操作中的剩下的转换操作和行动操作,最好把剩下的RDD编程都学完。 Spark【RDD编程(一)RDD编程基础】 RDD 转换操作 6、distinct 对 RDD 集合内部的元素进行去重…...
【2023最新版】MySQL安装教程
目录 一、MySQL简介 二、MySQL安装 1. 官网 2. 下载 3. 安装 4. 配置环境变量 配置前 配置中 配置后 5. 验证 一、MySQL简介 MySQL是一种开源的关系型数据库管理系统(RDBMS),它被广泛用于存储和管理结构化数据。MySQL提供了强大的功…...

关于mysql数据文件损坏导致的mysql无法启动的问题
环境 rocky linux 9 (跟centos几乎一模一样) myqsl 8.0, 存储引擎使用innodb 问题描述 1. 服务器异常关机,重启启动后发现mysql无法连接,使用命令查看mysql状态: systemctl status mysqld 发现mysql服…...
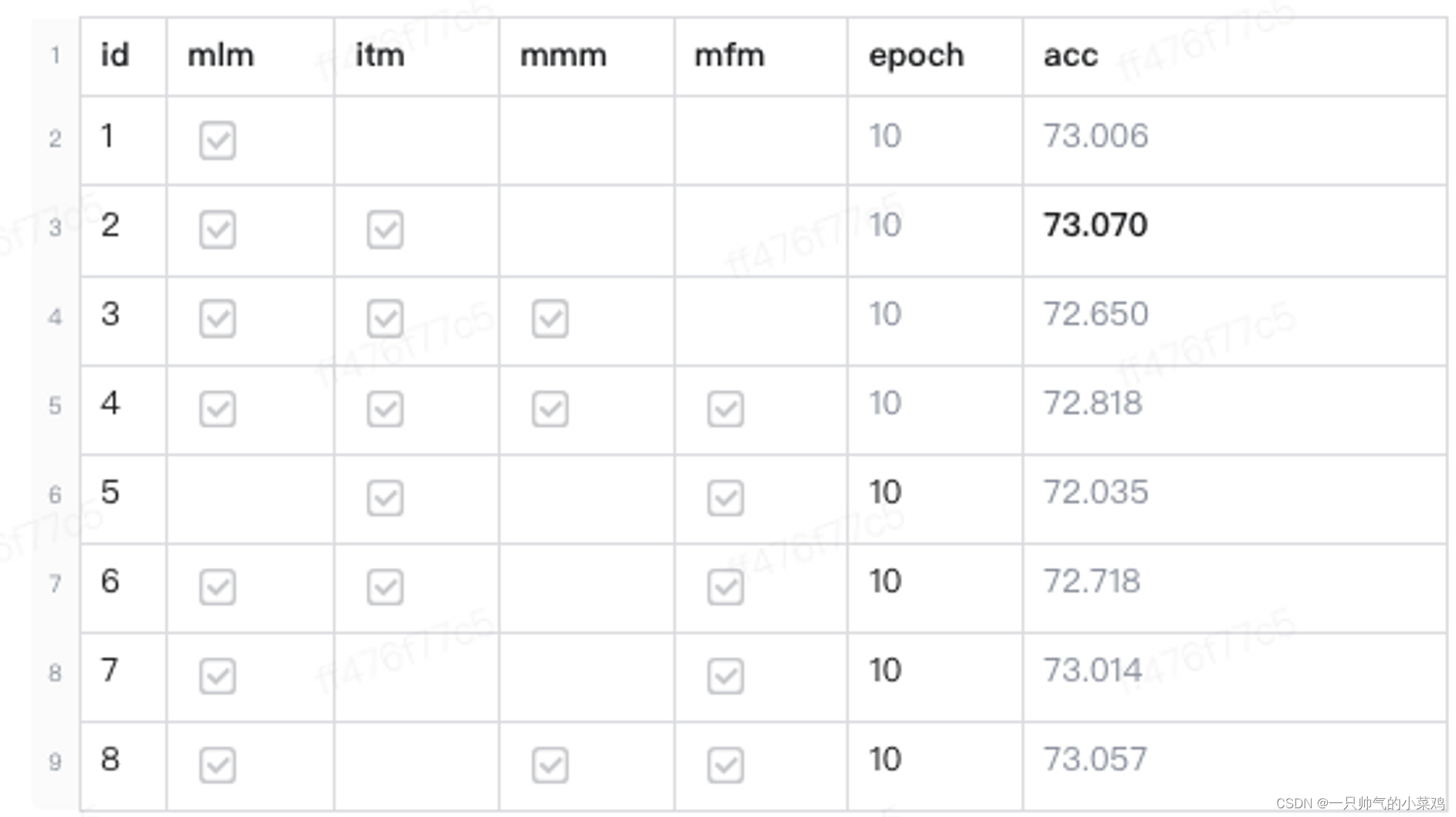
深度学习之视频分类项目小记
写在前面,最近一阵在做视频分类相关的工作,趁有时间来记录一下。本文更注重项目实战与落地,而非重点探讨多模/视频模型结构的魔改 零、背景 目标:通过多模态内容理解技术,构建视频层级分类体系原技术方案:…...
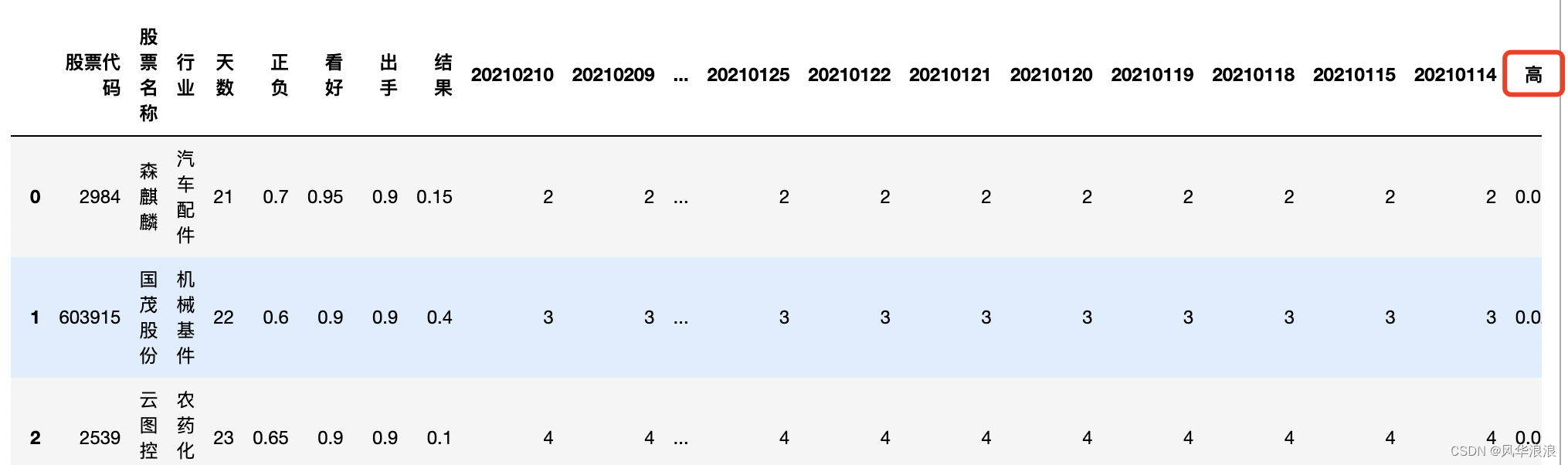
pandas(四十三)Pandas实现复杂Excel的转置合并
一、Pandas实现复杂Excel的转置合并 读取并筛选第一张表 df1 pd.read_excel("第一个表.xlsx") df1# 删除无用列 df1 df1[[股票代码, 高数, 实际2]].copy() df1df1.dtypes股票代码 int64 高数 float64 实际2 int64 dtype: object读取并处理第二张表…...
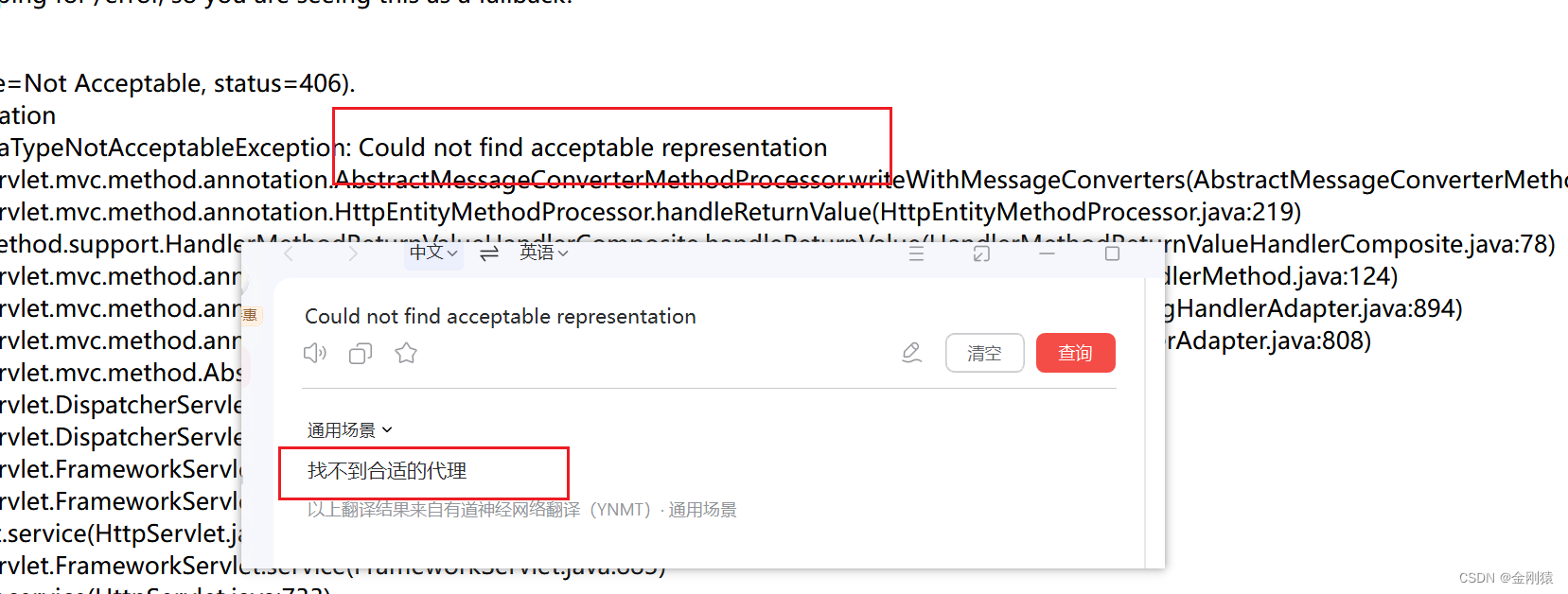
42、springboot 的 路径匹配 和 内容协商
springboot 的 路径匹配 和 内容协商 对于路径匹配,自己的总结就是: 以前路径匹配时默认不检查后缀,http://localhost:8080/aaa.json 可以直接访问到 RequstMapping(“/aaa”) 的方法。现在不行了。现在会检查后缀了。 内容协商的理解总结&…...

一文讲解Linux内核内存管理架构
内存管理子系统可能是linux内核中最为复杂的一个子系统,其支持的功能需求众多,如页面映射、页面分配、页面回收、页面交换、冷热页面、紧急页面、页面碎片管理、页面缓存、页面统计等,而且对性能也有很高的要求。本文从内存管理硬件架构、地址…...

教你如何使用API接口获取数据
随着互联网技术的发展和应用的普及,越来越多的系统和应用提供API接口供其他系统和应用进行数据交互。通过API接口,我们可以获取到各种各样的数据,例如天气预报、股票行情、新闻摘要等等。本文将介绍如何使用API接口获取数据,并附有…...
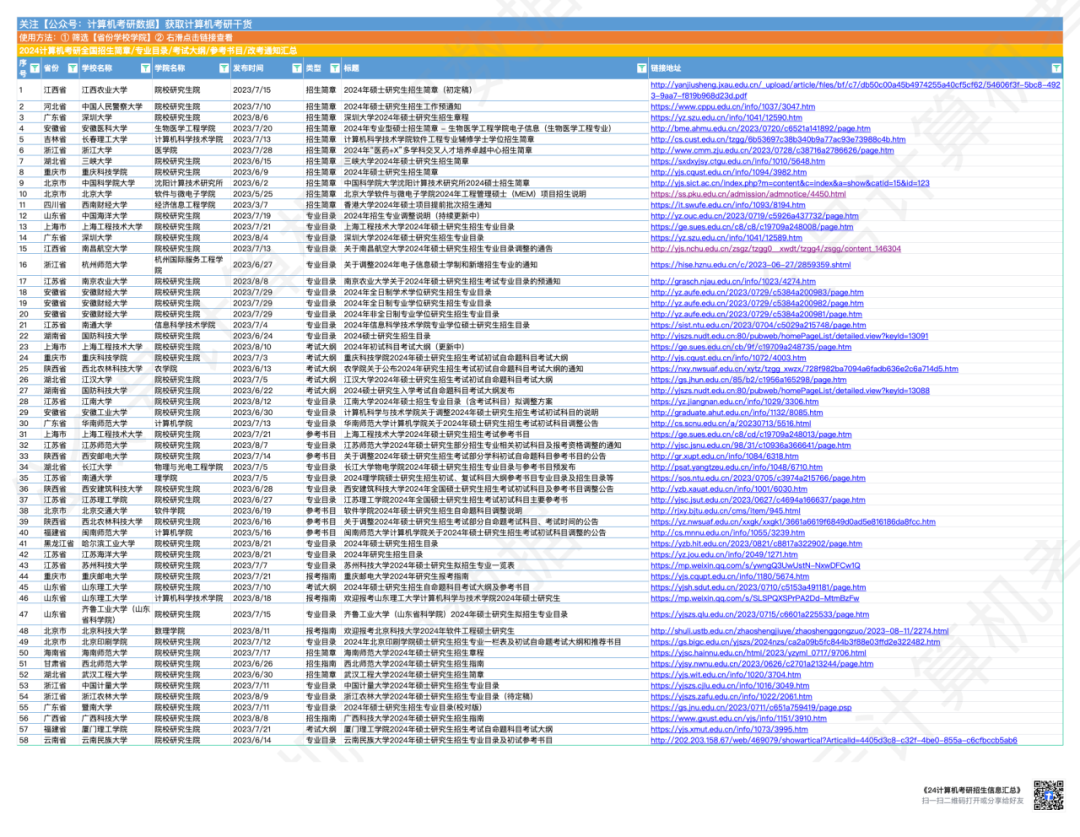
集美大学计算机改考408!福建省全面改考,仅剩一个自命题院校
9月5日,集美大学发布通知,0835软件工程、0854电子信息2024考试科目发生变更!由822数据结构调整为408计算机学科专业基础 https://zsb.jmu.edu.cn/info/1532/4701.htm 直接由一门改为考四门,难度升级不小。 目前福建省内计算机考…...
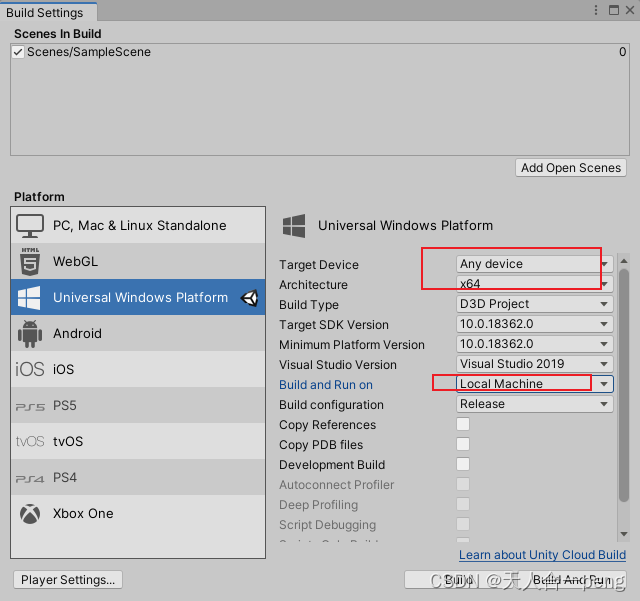
Hololens2部署很慢可能是unity工程选择不对
这样就很快,几分钟就完成了。(虽然又遇到新问题了) 第一次使用时如下,直接运行了一个多小时还没有完...

群论学习记录
群论学习记录 1. 2023.09.07 1. 2023.09.07 群论 (Group Theory) 终极速成 / 物理系零基础火箭级 notes https://zhuanlan.zhihu.com/p/378039151 https://zhuanlan.zhihu.com/p/164653537 群的定义重排定理子群陪集定理:由重排定理可推出1.4-(2&#x…...

Fiddler安装与使用教程(2) —— 软测大玩家
😏作者简介:博主是一位测试管理者,同时也是一名对外企业兼职讲师。 📡主页地址:【Austin_zhai】 🙆目的与景愿:旨在于能帮助更多的测试行业人员提升软硬技能,分享行业相关最新信息。…...

ChatGPT集锦
目录 1. 一条指令让ChatGPT变的更强大2. 对ChatGPT提问时,常见的10种错误描述3. Custom instructions如何设置1. 一条指令让ChatGPT变的更强大 在使用GPT的过程中,如何让AI更清晰地了解你的需求很重要?今天分享一个指令,可以让GPT成为你的好同事,与你一起分析和解决问题,…...
CRM系统中的工作流管理及其重要性
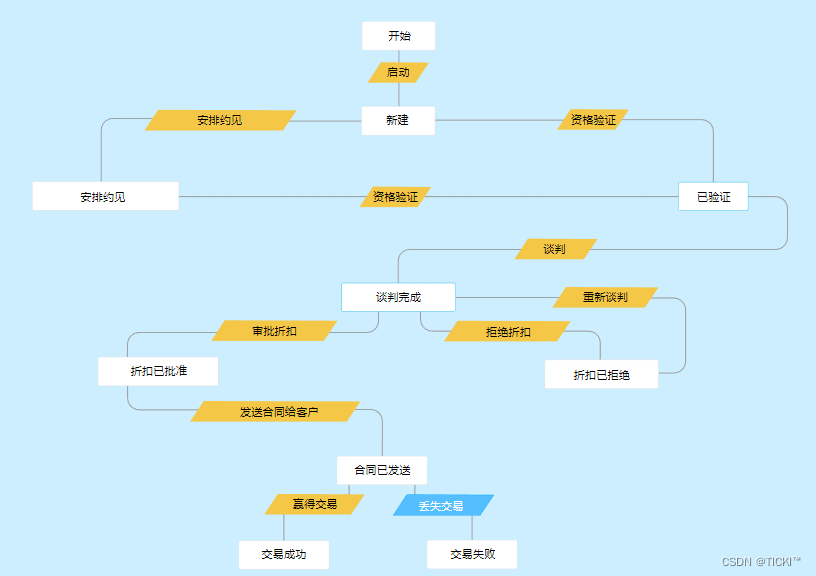
工作流是CRM系统中较为常见的功能,它可以有效减少重复工作、提高销售效率。如果您想深入了解,本文就来详细说说,CRM工作流是什么?工作流的作用? 什么是CRM工作流? CRM工作流是指在CRM系统中,根…...
Go framework-go-zero
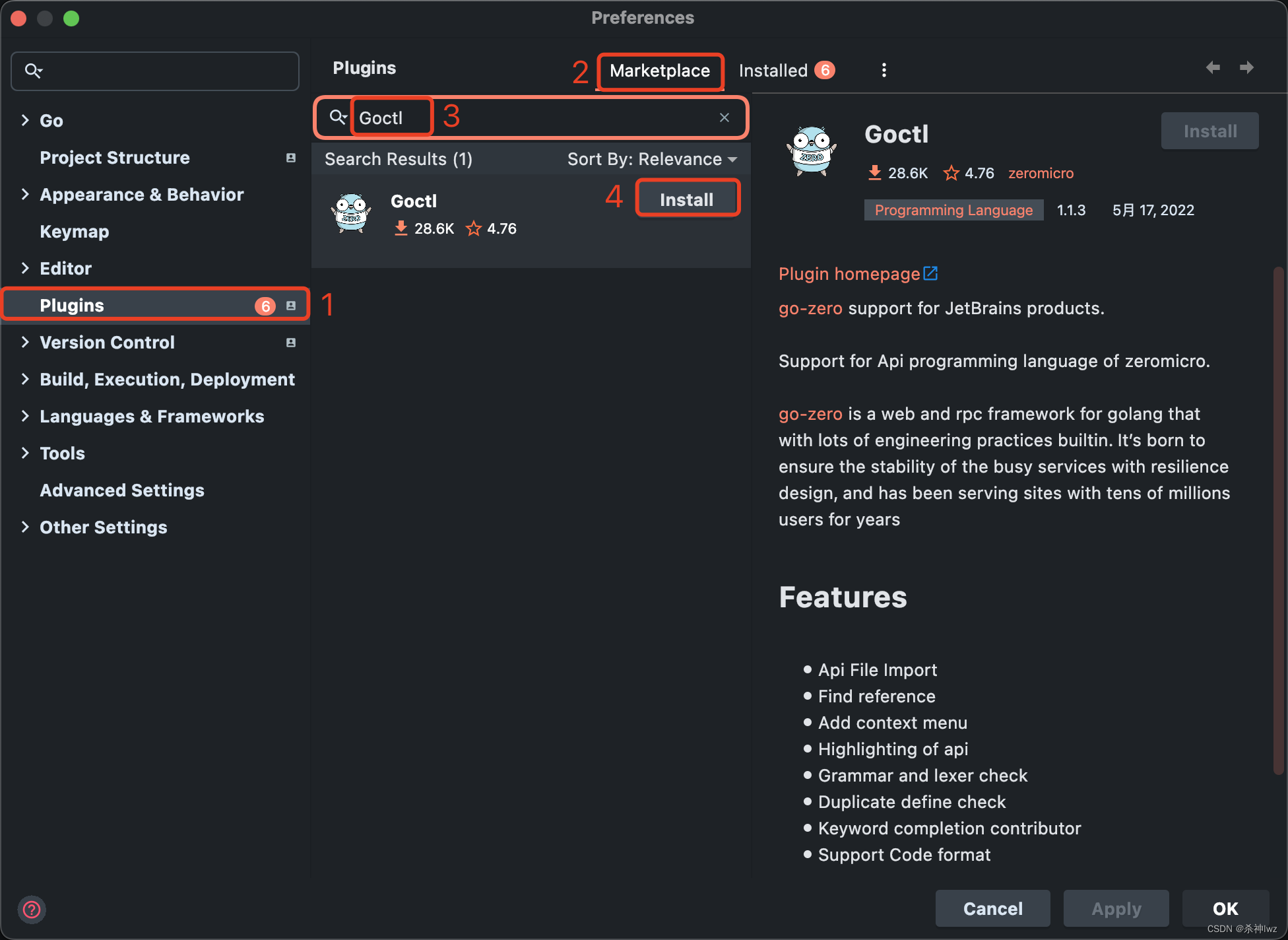
一、Go Go天然适配云原生,而云原生时代已经到来,各个应用组件基础设施等都应该积极的去拥抱云原生。 不要让框架束缚开发。 1、go-zero介绍 go-zero 是一个集成了各种工程实践的 web 和 rpc 框架。通过弹性设计保障了大并发服务端的稳定性,…...
【Python】【Fintech】用Python和蒙特卡洛法预测投资组合未来收益
【背景】 想利用蒙特卡洛方法和yahoo,stooq等财经网站上的数据快速预测特定portfolio的收益。 【分析】 整个程序的功能包括 读取json中的portfolio组合创建蒙特卡洛模拟预测收益的算法创建从财经网站获得特定投资组合数据,并根据2的算法获得该Index或Portfolio收益预测结…...
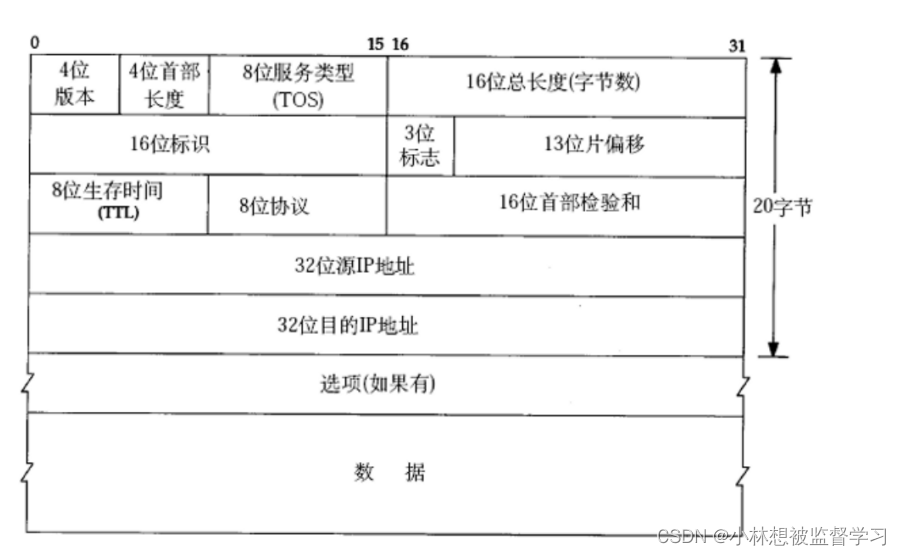
网络层重点协议-IP协议(结构分析)
IP协议数据报格式 一.4位版本号 用来表示IP协议的版本,现有的IP协议只有两个版本IPv4和IPv6 二.4位首部长度 IP协议数据报报头的长度 三.8位服务类型 3位优先权字段(已经弃用),4位TOS字段,和1位保留 字段(必…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...
)
Leetcode33( 搜索旋转排序数组)
题目表述 整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k1], …, nums[n-1], nums[0], nu…...
