代码随想录训练营第五十七天|647. 回文子串、516.最长回文子序列
647. 回文子串
题目链接/文章讲解/视频讲解:代码随想录
1.代码展示
//647.回文子串
int countSubstrings(string s) {//step1 构建dp数组,明确dp数组的含义,dp[i][j]的含义是在下标为i和j区间内的字串是否为回文串vector<vector<bool>> dp(s.size(), vector<bool>(s.size(), false));//step2 构建状态转移方程//当s[i] != s[j]时,此时必定不为回文子串//当s[i] == s[j]时,有三种情况//情况一:i = j,此时就是本身,因此必定为回文子串//情况二:i + 1 = j,此时就如aa的形式,因此也是回文子串//情况三:j > i + 1,此时当dp[i + 1][j - 1]为回文字串时,dp[i][j]才是回文子串//step3 初始化dp数组,都为false//step4 开始遍历int nResult = 0;for (int i = s.size() - 1; i >= 0; i++) {for (int j = i; j < s.size(); j++) {if (s[i] == s[j]) {if (j - i <= 1) {nResult++;dp[i][j] = true;}else if (dp[i + 1][j - 1]){nResult++;dp[i][j] = true;}}}}return nResult;
}2.本题小节
思考:本题的重点在于对于dp[i][j]的理解,dp[i][j]的含义是在下标为i和j区间内的字串是否为回文串。构建状态转移方程,当s[i] != s[j]时,此时必定不为回文子串;当s[i] == s[j]时,有三种情况
,情况一,i = j,此时就是本身,因此必定为回文子串, 情况二,i + 1 = j,此时就如aa的形式,因此也是回文子串,情况三:j > i + 1,此时当dp[i + 1][j - 1]为回文字串时,dp[i][j]才是回文子串;初始化都为false,最后注意遍历顺序,先下后上,先左后右。
基本思路:注意理解dp[i][j]的含义,按照代码的思路来即可。
516.最长回文子序列
题目链接/文章讲解/视频讲解:代码随想录
1.代码展示
//516.最长回文子序列
int longestPalindromeSubseq(string s) {//step1 构建dp数组,dp[i][j]的含义是在[i,j]下标的范围内s的最长回文子序列vector<vector<int>> dp(s.size(), vector<int>(s.size(), 0));//step2 状态转移方程//当s[i] == s[j],dp[i][j] = dp[i + 1][j - 1] + 2,//不等时,有两种情况,说明同时加入s[i],s[j]不能满足情况,分别加入s[i]和s[j]试试//则dp[i][j] = max(dp[i][j - 1], dp[i + 1][j])//step3 初始化for (int i = 0; i < s.size(); i++) {dp[i][i] = 1;}//step4 开始遍历for (int i = s.size() - 1; i >= 0; i++) {for (int j = i + 1; j < s.size(); j++) {if (s[i] == s[j]) {dp[i][j] = dp[i + 1][j - 1] + 2;}else {dp[i][j] = max(dp[i][j - 1], dp[i + 1][j]);}}}return dp[0][s.size() - 1];
}2.本题小节
思考:明确dp数组的含义。dp[i][j]的含义是在[i,j]下标的范围内s的最长回文子序列。状态转移方程,当s[i] == s[j],dp[i][j] = dp[i + 1][j - 1] + 2,不等时,有两种情况,说明同时加入s[i],s[j]不能满足情况,分别加入s[i]和s[j]试试,则dp[i][j] = max(dp[i][j - 1], dp[i + 1][j]),初始化时对角线都为1,根据dp数组可以得。遍历时先下后上,先左后右。
基本思路:注意dp数组的含义,按照动态规划步骤来。
动态规划总结:代码随想录
相关文章:

代码随想录训练营第五十七天|647. 回文子串、516.最长回文子序列
647. 回文子串 题目链接/文章讲解/视频讲解:代码随想录 1.代码展示 //647.回文子串 int countSubstrings(string s) {//step1 构建dp数组,明确dp数组的含义,dp[i][j]的含义是在下标为i和j区间内的字串是否为回文串vector<vector<bool&…...
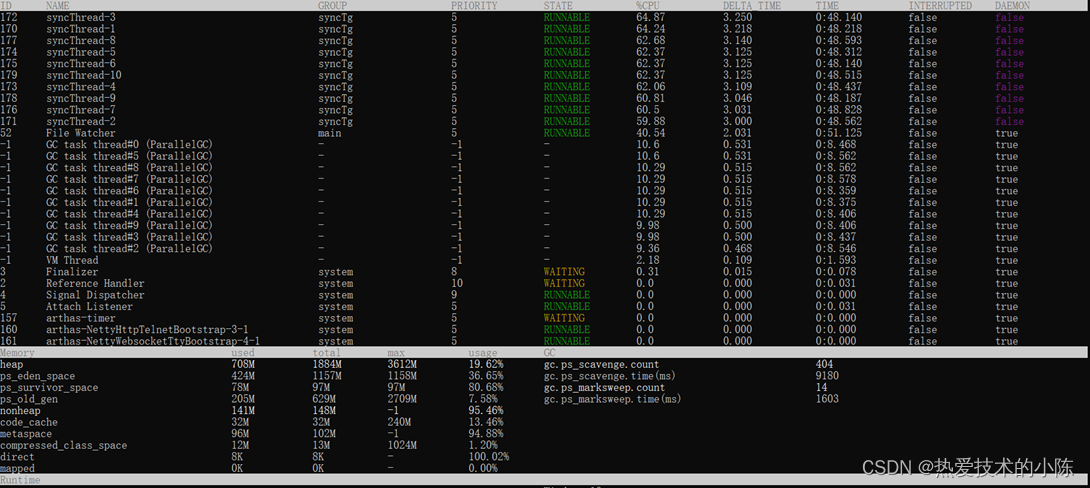
对线程池设置做压测
线程池代码 Configuration public class ThreadPoolConfig {// 核心线程池大小private int corePoolSize 24;// 最大可创建的线程数private int maxPoolSize 25;// 队列最大长度private int queueCapacity 100;// 线程池维护线程所允许的空闲时间private int keepAliveSeco…...

【网络通信 -- WebRTC】项目实战记录 -- mediasoup android 适配 webrtc m94
【网络通信 -- WebRTC】项目实战记录 -- mediasoup android 适配 webrtc m94 【1】下载并配置 depot_tools 下载 depot_tools git clone https://chromium.googlesource.com/chromium/tools/depot_tools.git编辑 ~/.bashrc 将 depot_tools 添加到路径中 vim ~/.bashrc export…...
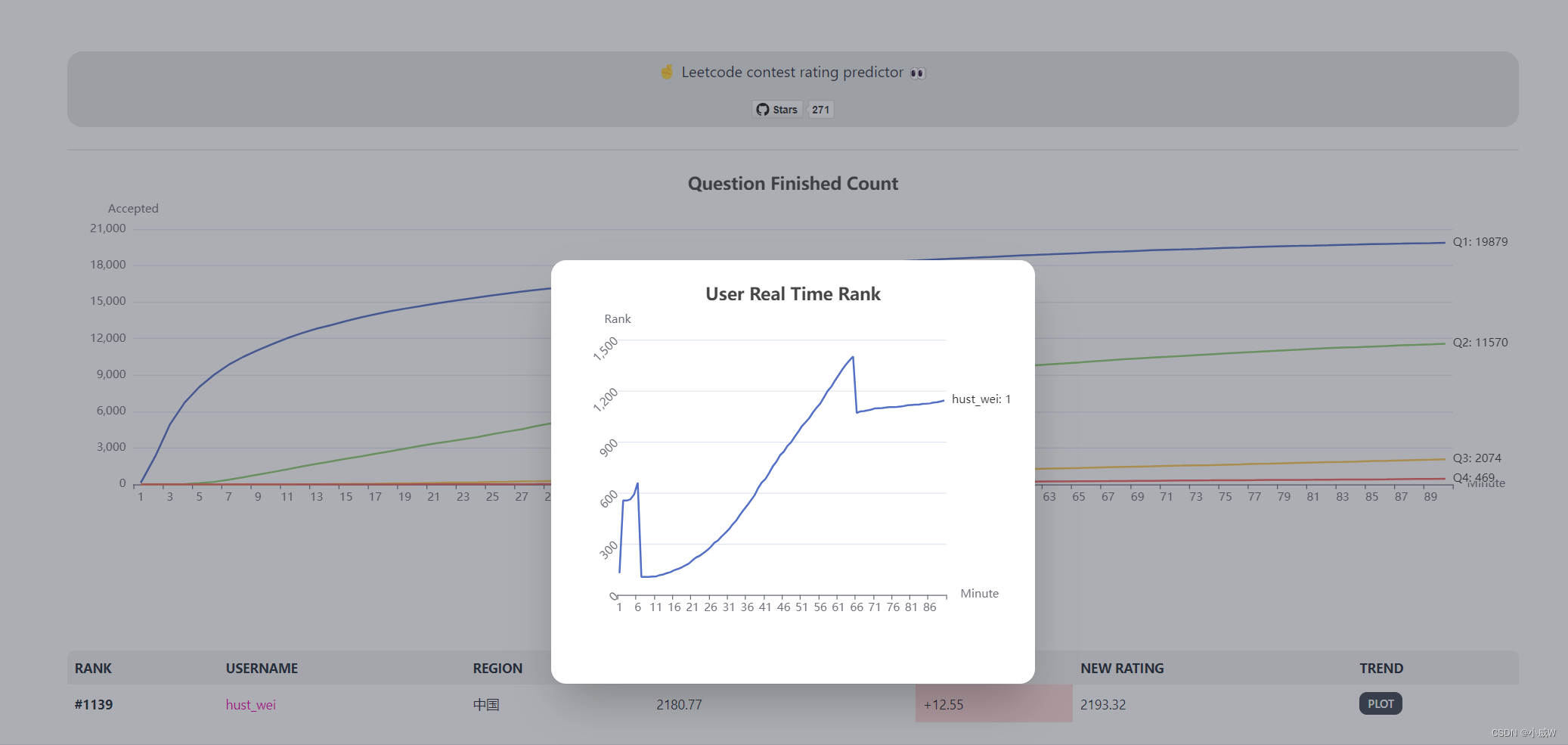
【力扣周赛】第 357 场周赛(⭐反悔贪心)
文章目录 竞赛链接Q1:6925. 故障键盘解法1——直接模拟解法2——双端队列 Q2:6953. 判断是否能拆分数组(贪心)Q3:2812. 找出最安全路径⭐解法1——多源BFS瓶颈路模型?解法2——多源BFS 倒序枚举答案 并查…...

css重置
css 重置 CSS 重置的主要目标是确保浏览器之间的一致性,并撤消所有默认样式,创建一个空白板。 如今,主流浏览器都实现了css规范,在布局或间距方面没有太大差异。但是通过自定义 CSS 重置,也可以改善用户体验和提高开…...

tcpdump相关
Linux内核角度分析tcpdump原理(一)Linux内核角度分析tcpdump原理(二)...

MFC新建内部消息
提示:记录一下MFC新建内部消息的成功过程 文章目录 前言一、pandas是什么?二、使用步骤 1.引入库2.读入数据总结 前言 先说一下基本情况,因为要在mapview上增加一个显示加载时间的功能。然后发现是要等加载完再显示时间,显示在主…...

linux查找目录
要在Linux中查找目录,可以使用find命令。下面是查询目录的几个示例: 1,查找当前目录下所有子目录: find . -type d 2,在指定路径下查找目录: find /path/to/directory -type d 3,查找以特定名称开头的目录: find . -t…...
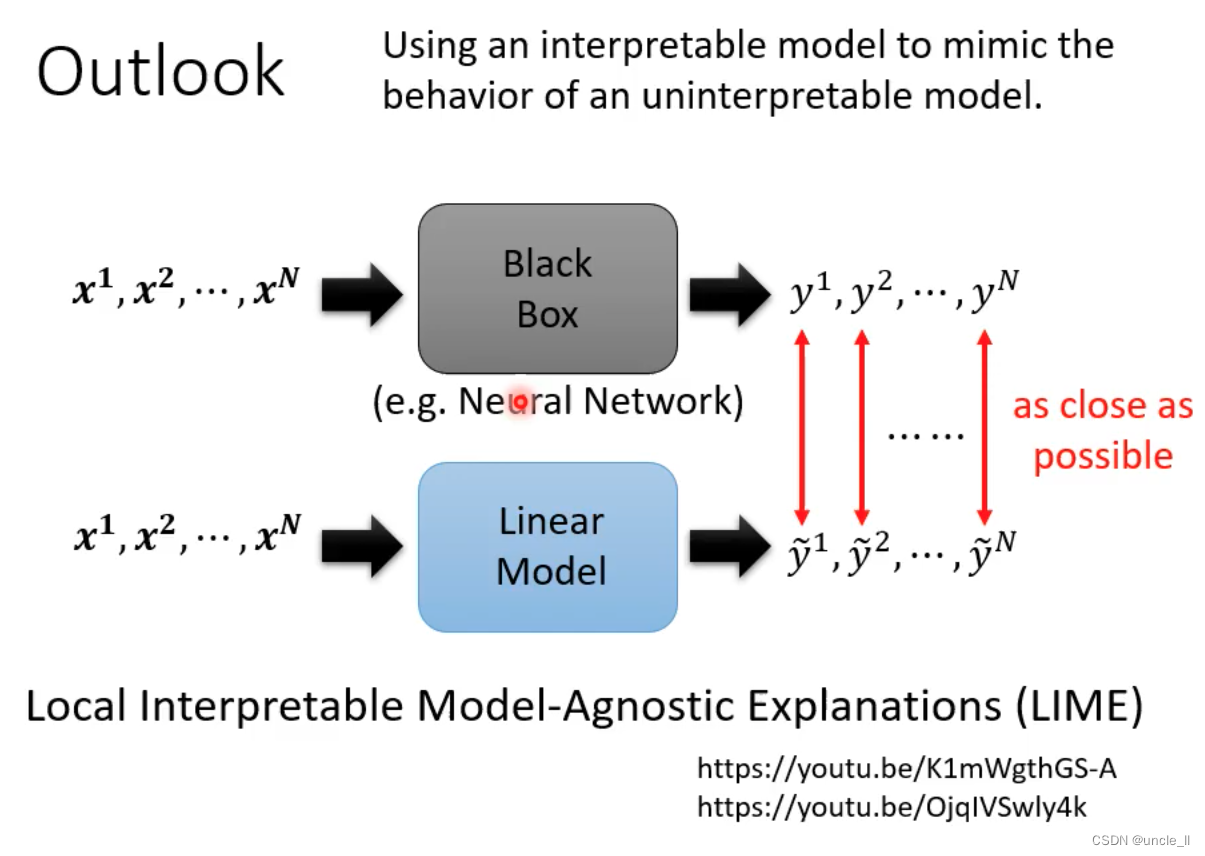
机器学习:可解释学习
文章目录 可解释学习为什么需要可解释机器学习可解释还是强模型可解释学习的目标可解释机器学习Local ExplanationGlobal Explanation 可解释学习 神马汉斯,只有在有人看的时候能够答对。 为什么需要可解释机器学习 贷款,医疗需要给出理由,让…...

UE5- c++ websocket里实现调用player里的方法
# UGameInstance里直接调用 获取到引用了,就可以自然的调用。忽略 # UGameInstance里间接调用,通过代理调用 前置已经添加了websocket,具体步骤参考,链接在UWebSocketGameInstance.h里新增代理,并在链接成功后进行绑定。 #pragma…...
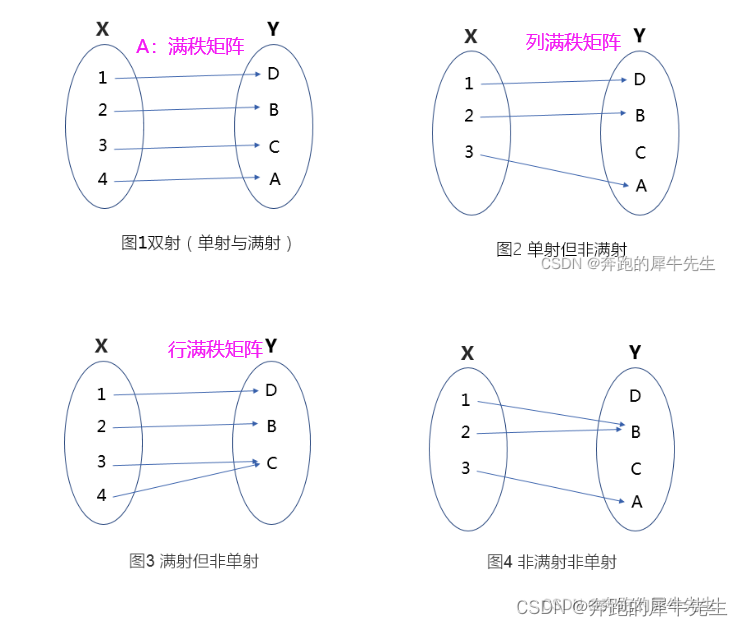
线性代数的学习和整理18:什么是维度,什么是秩?秩的各种定理秩的计算 (计算部分未完成)
目录 0 问题引出:什么是秩? 概念备注: 1 先厘清:什么是维数? 1.1 真实世界的维度数 1.2 向量空间的维数 1.2.1 向量空间,就是一组最大线性无关的向量组/基张成的空间 1.3 向量α的维数 1.3.1 向量的…...
Centos 6.5 升级到Centos7指导手册
一、背景 某业务系统因建设较早,使用的OS比较过时,还是centos6.5的系统,因国产化需要,需将该系统升级到BClinux 8.6,但官方显示不支持centos 6.x升级到8,需先将centos6.5升级到centos7的最新版,…...

详解python中的映射类型---字典
概述 映射类型是“键-值”数据项的组合,每个元素是一个键值对,即元素是(key,value),元素之间是无序的。键值对(key,value)是一种二元关系,源于属性和值的映射…...

gdal求矢量图形的形心
gdal求矢量图形的形心 #include "gdal_priv.h" #include "ogrsf_frmts.h"int main() {OGRRegisterAll();OGRPolygon* square_1 new OGRPolygon();OGRLinearRing* ring_1 new OGRLinearRing();// 添加 square_1 的点ring_1->addPoint(0, 0);ring_1-&g…...

<深度学习基础> Batch Normalization
Batch Normalization批归一化 BN优点 减少了人为选择参数。在某些情况下可以取消dropout和L2正则项参数,或者采取更小的L2正则项约束参数;减少了对学习率的要求。现在我们可以使用初始很大的学习率或者选择了较小的学习率,算法也能够快速训…...
Ubuntu yolov5 环境配置
查看Ubuntu版本 $ cat /proc/version Linux version 5.4.0-150-generic (builddbos03-amd64-012) (gcc version 7.5.0 (Ubuntu 7.5.0-3ubuntu1~18.04)) #167~18.04.1-Ubuntu SMP Wed May 24 00:51:42 UTC 2023虚拟机磁盘扩容 因为在环境搭建过程中遇到了磁盘空间不足的问题&a…...
【自执行闭包JS逆向】某网站登录MD5加密分析
文章目录 一、写在前面二、抓包分析三、加密函数分析 一、写在前面 最近工作比较忙,不过还是在督促自己利用有限的时间学习更新一些技术文章。互联网这个行业大家目前也都知道是非常内卷的,所有大家在工作之余养成良好的自主学习习惯是非常好的ÿ…...
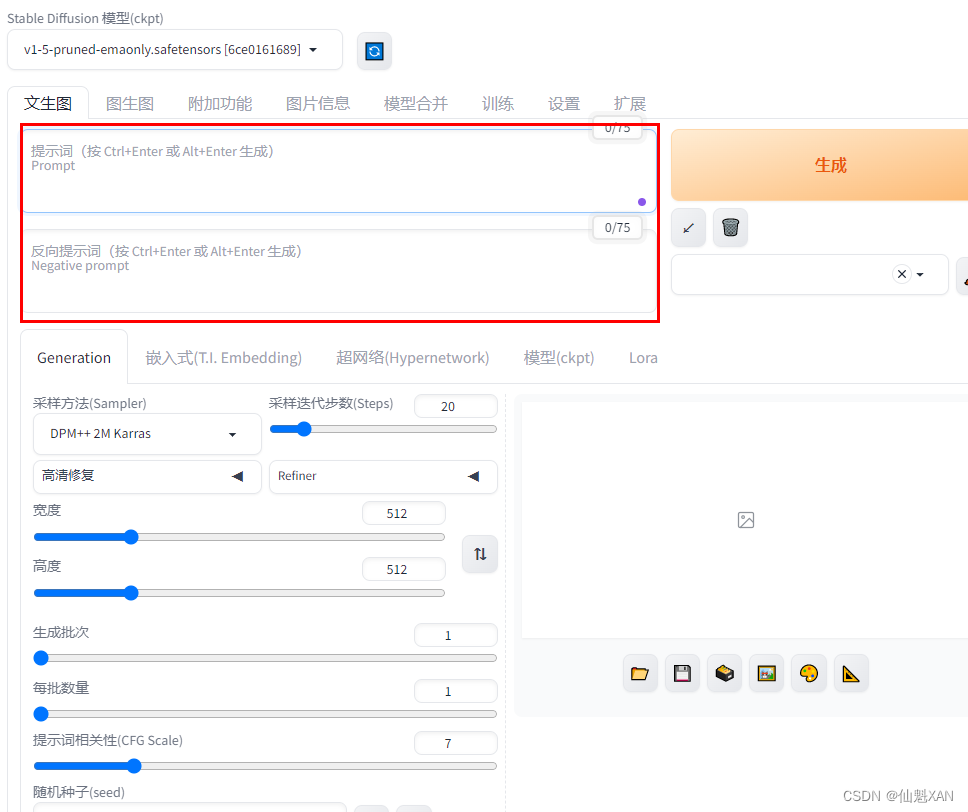
Stable Diffuse 之 安装文件夹、以及操作界面 UI 、Prompt相关说明
Stable Diffuse 之 安装文件夹、以及操作界面 UI 、Prompt相关说明 目录 Stable Diffuse 之 安装文件夹、以及操作界面 UI 、Prompt相关说明 一、简单介绍 二、安装文件相关说明 三、界面的简单说明 四、prompt 的一些语法简单说明 1、Prompt :正向提示词 &am…...

【Linux】- 一文秒懂shell编程
shell编程 1.1 Shell 是什么1.2 Shell 脚本的执行方式1.3 编写第一个 Shell 脚本2.1 Shell 的变量2.2 shell 变量的定义2.3 设置环境变量3.1 位置参数变量3.2 预定义变量4.1 运算符4.2 条件判断5.1 流程控制5.2 case 语句5.3 for 循环5.4 while 循环5.5 read基本语法6.1函数6.2…...

CentOS下多网卡绑定多IP段时导致只有一个会通的问题解决
CentOS下多网卡绑定多IP段时导致只有一个会通的问题解决 虚拟机配置多个网络地址,结果同时只能有一个ip是通的, 原因:Linux默认开启了反向路由检查导致的,比如说外面访问eth0的网卡,而网关在eth1上,又或者从…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

离线语音识别方案分析
随着人工智能技术的不断发展,语音识别技术也得到了广泛的应用,从智能家居到车载系统,语音识别正在改变我们与设备的交互方式。尤其是离线语音识别,由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力,广…...

水泥厂自动化升级利器:Devicenet转Modbus rtu协议转换网关
在水泥厂的生产流程中,工业自动化网关起着至关重要的作用,尤其是JH-DVN-RTU疆鸿智能Devicenet转Modbus rtu协议转换网关,为水泥厂实现高效生产与精准控制提供了有力支持。 水泥厂设备众多,其中不少设备采用Devicenet协议。Devicen…...

加密通信 + 行为分析:运营商行业安全防御体系重构
在数字经济蓬勃发展的时代,运营商作为信息通信网络的核心枢纽,承载着海量用户数据与关键业务传输,其安全防御体系的可靠性直接关乎国家安全、社会稳定与企业发展。随着网络攻击手段的不断升级,传统安全防护体系逐渐暴露出局限性&a…...

【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅!
【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅! 🌱 前言:一棵树的浪漫,从数组开始说起 程序员的世界里,数组是最常见的基本结构之一,几乎每种语言、每种算法都少不了它。可你有没有想过,一组看似“线性排列”的有序数组,竟然可以**“长”成一棵平衡的二…...
