A - Orac and Models(最长上升子序列——加强版)
There are nn models in the shop numbered from 11 to nn, with sizes s_1, s_2, \ldots, s_ns1,s2,…,sn.
Orac will buy some of the models and will arrange them in the order of increasing numbers (i.e. indices, but not sizes).
Orac thinks that the obtained arrangement is beatiful, if for any two adjacent models with indices i_jij and i_{j+1}ij+1 (note that i_j < i_{j+1}ij<ij+1, because Orac arranged them properly), i_{j+1}ij+1 is divisible by i_jij and s_{i_j} < s_{i_{j+1}}sij<sij+1.
For example, for 66 models with sizes \{3, 6, 7, 7, 7, 7\}{3,6,7,7,7,7}, he can buy models with indices 11, 22, and 66, and the obtained arrangement will be beautiful. Also, note that the arrangement with exactly one model is also considered beautiful.
Orac wants to know the maximum number of models that he can buy, and he may ask you these queries many times.
Input
The first line contains one integer t\ (1 \le t\le 100)t (1≤t≤100): the number of queries.
Each query contains two lines. The first line contains one integer n\ (1\le n\le 100\,000)n (1≤n≤100000): the number of models in the shop, and the second line contains nn integers s_1,\dots,s_n\ (1\le s_i\le 10^9)s1,…,sn (1≤si≤109): the sizes of models.
It is guaranteed that the total sum of nn is at most 100\,000100000.
Output
Print tt lines, the ii-th of them should contain the maximum number of models that Orac can buy for the ii-th query.
Sample 1
| Inputcopy | Outputcopy |
|---|---|
4 4 5 3 4 6 7 1 4 2 3 6 4 9 5 5 4 3 2 1 1 9 | 2 3 1 1 |
Note
In the first query, for example, Orac can buy models with indices 22 and 44, the arrangement will be beautiful because 44 is divisible by 22 and 66 is more than 33. By enumerating, we can easily find that there are no beautiful arrangements with more than two models.
In the second query, Orac can buy models with indices 11, 33, and 66. By enumerating, we can easily find that there are no beautiful arrangements with more than three models.
In the third query, there are no beautiful arrangements with more than one model.、、
题目翻译:
给出n个数的值,求出满足下标j整除i并且a[j]>a[i]的最多个数(j>i)
#include<iostream>
#include<algorithm>
#include<map>
#include<cstring>
#include<vector>
#include<cmath>
#include<cstdlib>using namespace std;
const int N = 1e5 + 10;int a[N],b[N];//DP:b[i]表示以i结尾的子序列的长度int main()
{int t; cin >> t;while (t--){int n; cin >> n;for (int i = 1; i <= n; i++) cin >> a[i]; //读入数据for (int i = 1; i <= n; i++) b[i] = 1;for (int i = 1; i <= n; i++)for (int j = 2 * i; j <= n; j += i) //满足条件1:j是i的倍数,j可以整除iif (a[i] < a[j]) b[j] = max(b[j], b[i] + 1); //满足条件2:a[j]>a[i]//DP:以选不选第j个数作为比较,求最大的那个//选j:长度为j的上一个数i加1,即b[i]+1;//不选j:即b[j]int ans = -INT_MAX;for (int i = 1; i <= n; i++) ans = max(ans, b[i]);cout << ans << endl;}}相关文章:
)
A - Orac and Models(最长上升子序列——加强版)
There are nn models in the shop numbered from 11 to nn, with sizes s_1, s_2, \ldots, s_ns1,s2,…,sn. Orac will buy some of the models and will arrange them in the order of increasing numbers (i.e. indices, but not sizes). Orac thinks that the obtai…...
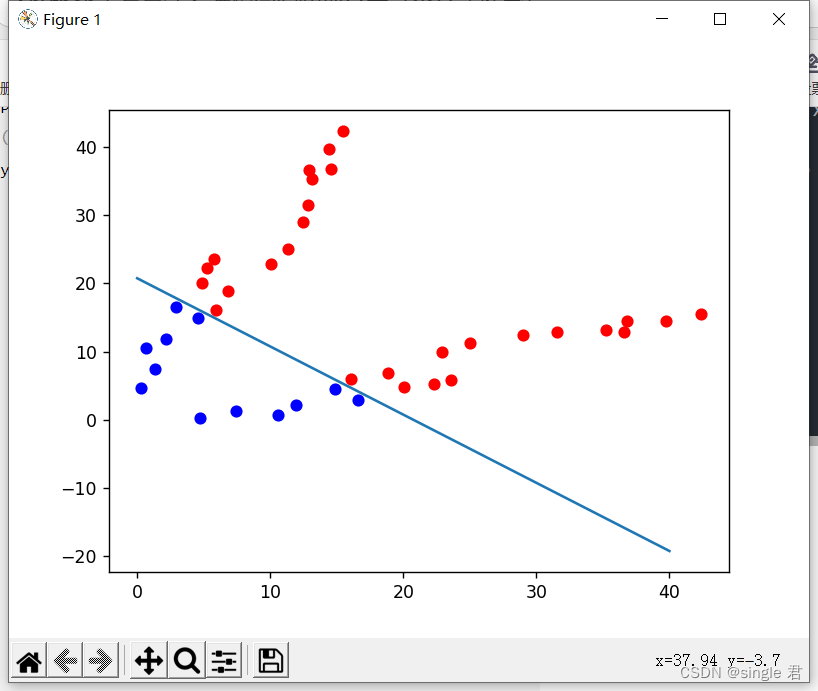
【python手写算法】逻辑回归实现分类(含公式推导)
公式推导: 代码实现: # codingutf-8 import matplotlib.pyplot as plt import numpy as npdef f(w1,x1,w2,x2,b):zw1*x1w2*x2breturn 1/(1np.exp(-z)) if __name__ __main__:X1 [12.46, 0.25, 5.22, 11.3, 6.81, 4.59, 0.66, 14.53, 15.49, 14.43,2.1…...

【2023高教社杯数学建模国赛】ABCD题 问题分析、模型建立、参考文献及实现代码
【2023高教社杯数学建模国赛】ABCD题 问题分析、模型建立、参考文献及实现代码 1 比赛时间 北京时间:2023年9月7日 18:00-2023年9月10日20:00 2 思路内容 可以参考我提供的历史竞赛信息内容,最新更新我会发布在博客和知乎上,请关注我获得最…...

yum安装mysql5.7散记
## 数据源安装 $ yum -y install wget $ wget http://dev.mysql.com/get/mysql57-community-release-el7-8.noarch.rpm $ yum localinstall mysql57-community-release-el7-8.noarch.rpm $ yum repolist enabled | grep "mysql.*-community.*" $ yum install mysql-…...
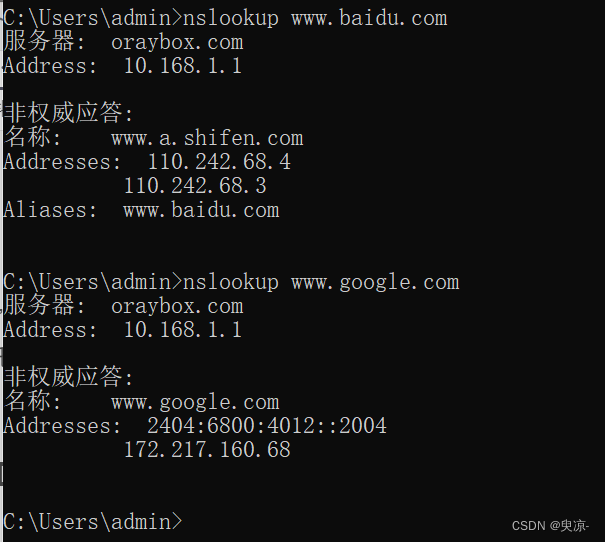
DNS解析
1.DNS介绍 DNS 表示域名系统。此系统实质上是用于整理和识别各个域名的网络电话簿。电话簿将“Acme Pizza”之类的名称转换为要拨打的正确电话号码,而 DNS 将“www.google.com”之类的网络地址转换为托管该网站的计算机的物理 IP 地址,如“74.125.19.147…...

从jdk8 升级到jdk17的问题总结
目录 1. java.lang.reflect.InaccessibleObjectException: 2. java.lang.UnsatisfiedLinkError in autosys 3. java.lang.NoClassDefFoundError: Could not initialize class net.sf.jasperreports.engine.util.JRStyledTextParser 4. java.lang.UnsatisfiedLinkError: **…...
一百七十二、Flume——Flume采集Kafka数据写入HDFS中(亲测有效、附截图)
一、目的 作为日志采集工具Flume,它在项目中最常见的就是采集Kafka中的数据然后写入HDFS或者HBase中,这里就是用flume采集Kafka的数据导入HDFS中 二、各工具版本 (一)Kafka kafka_2.13-3.0.0.tgz (二)…...
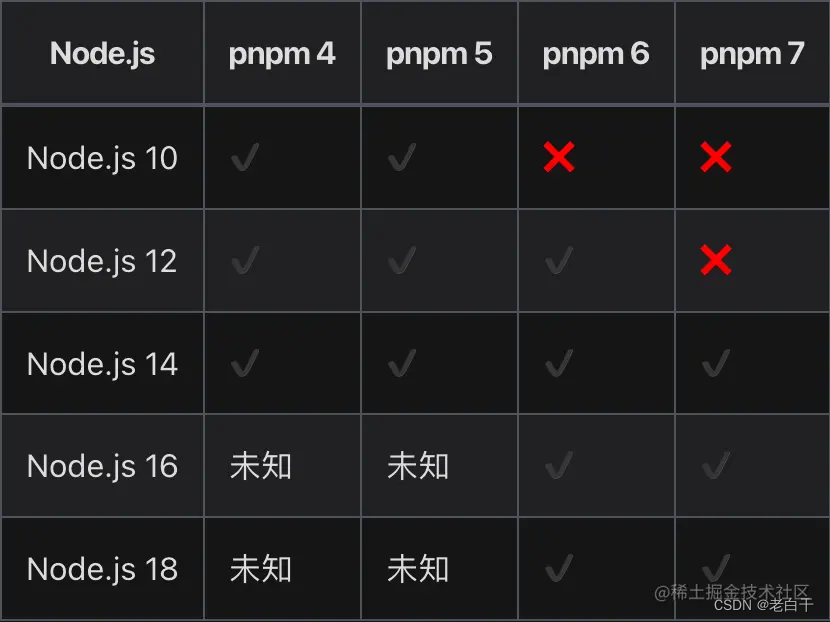
pnpm 升级
1. 在以下路径下删除pnpm包 2. 执行which pnpm,在结果目录中删除pnpm 3. sudo npm install -g pnpm 重新安装,node默认使用16...

有关使用HttpServletRequest的Cookie的设置和获取
文章目录 小结问题和解决参考 小结 介绍了如何在HttpServletRequest中对Cookie的进行设置和获取。 问题和解决 在服务器端的HttpServletRequest中对Cookie的进行设置后,客户端在接下来的请求中会携带此设置好的Cookie,所以可以在服务器端接收请求时提…...

关于 Nginx 的哪些事
关于 Nginx 的哪些事 1、Nginx 主要功能2、Nginx 的常用命令2.1、启动Nginx2.2、停止 Nginx2.3、重新加载Nginx 配置2.4、检查Nginx配置文件2.5、指定配置文件2.6、检查Nginx版本2.7、显示Nginx帮助信息 3、Nginx 配置文件 nginx.conf3.1、Nginx 配置文件(nginx.con…...

插入排序——希尔排序
1、简述: 希尔排序(Shells Sort)是插入排序的一种又称“缩小增量排序”(Diminishing Increment Sort),是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因 D.L.Shell 于 1959 年提出而得名。 希尔排…...
C语言之初阶总结篇
目录 NO.1 NO.2 NO.3 NO.4 NO.5 NO.6 NO.7 NO.8 NO.9 NO.10 NO.11 NO.12.概念tips NO.13.求最小公倍数 NO.14.最大公因数 NO.15.输入读取字符串 NO.16.倒置字符串 今天是一些C语言题目,最近天气炎热,多喝水。 NO.1 下面程序执行后&am…...

Android签名查看
查看签名文件信息 第一种方法: 1.打开cmd,执行keytool -list -v -keystore xxx.keystore,效果如下图: 第二种方法: 1.打开cmd,执行 keytool -list -v -keystore xxxx.keystore -storepass 签名文件密码࿰…...

Educational Codeforces Round 3
目录 A. USB Flash Drives B. The Best Gift C. Load Balancing D. Gadgets for dollars and pounds A. USB Flash Drives #include<bits/stdc.h>using namespace std; const int N1e65; typedef long long ll; typedef pair<ll,ll> pll; typedef array<int…...

Docker Compose常用命令
常用命令 1.1 restart, start, stop-- 启动和停止服务 命令必须在 docker-compose.yml文件所在的目录下执行。 # 前台启动, 启动项目中的所有服务。 $. docker-compose up# 后台启动, 启动所有服务并在后台运行。 $. docker-compose up -d# 停止所有服务。 $. docker-compose …...
C++——智能指针
智能指针 文章目录 智能指针内存泄漏智能指针解决内存泄漏问题智能指针的使用及原理RAII智能指针对象的拷贝问题 C中的智能指针auto_ptrunique_ptrshared_ptrweak_ptr定制包装器C11和boost中智能指针的关系 内存泄漏 什么是内存泄漏:内存泄漏指因为疏忽或错误造成程…...
CVE-2023-3836:大华智慧园区综合管理平台任意文件上传漏洞复现
文章目录 CVE-2023-3836:大华智慧园区综合管理平台任意文件上传漏洞复现0x01 前言0x02 漏洞描述0x03 影响范围0x04 漏洞环境0x05 漏洞复现1.访问漏洞环境2.构造POC3.复现 CVE-2023-3836:大华智慧园区综合管理平台任意文件上传漏洞复现 0x01 前言 免责声…...
LAMP搭建WordPress
L linux A apache hhtpd M mysql/maridb P PHP1、 安装php yum -y install php php-fpm php-server php-mysql1.1、 启动php-fpm并自启 systemctl enable php-fpm --now[rootecs-1cee ~]# systemctl status php-fpm ● php-fpm.service - The PHP FastCGI Process ManagerLoa…...

【数学建模竞赛】预测类赛题常用算法解析
解析常见的预测类算法 灰色预测模型 灰色预测模型是一种利用少量的、不完全的信息,建立数学模型并进行预测的方法。该方法通过对系统行为特征的发展变化规律进行估计预测,同时也可以对行为特征的异常情况发生的时刻进行估计计算,并研究特定…...
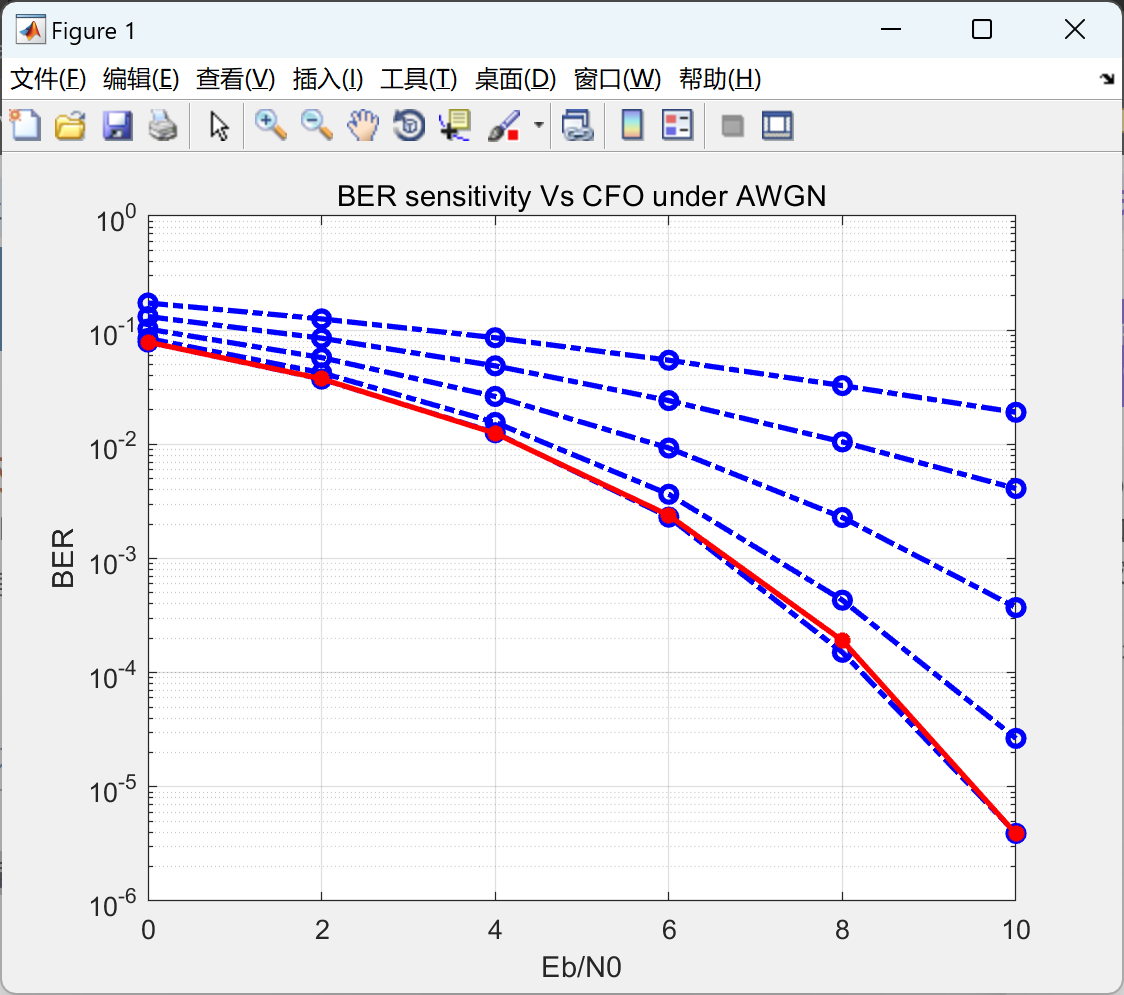
OFDM 系统在 AWGN 信道下对不同载波频率偏移 (CFO) 的 BER 灵敏度研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...
