【数学建模竞赛】预测类赛题常用算法解析
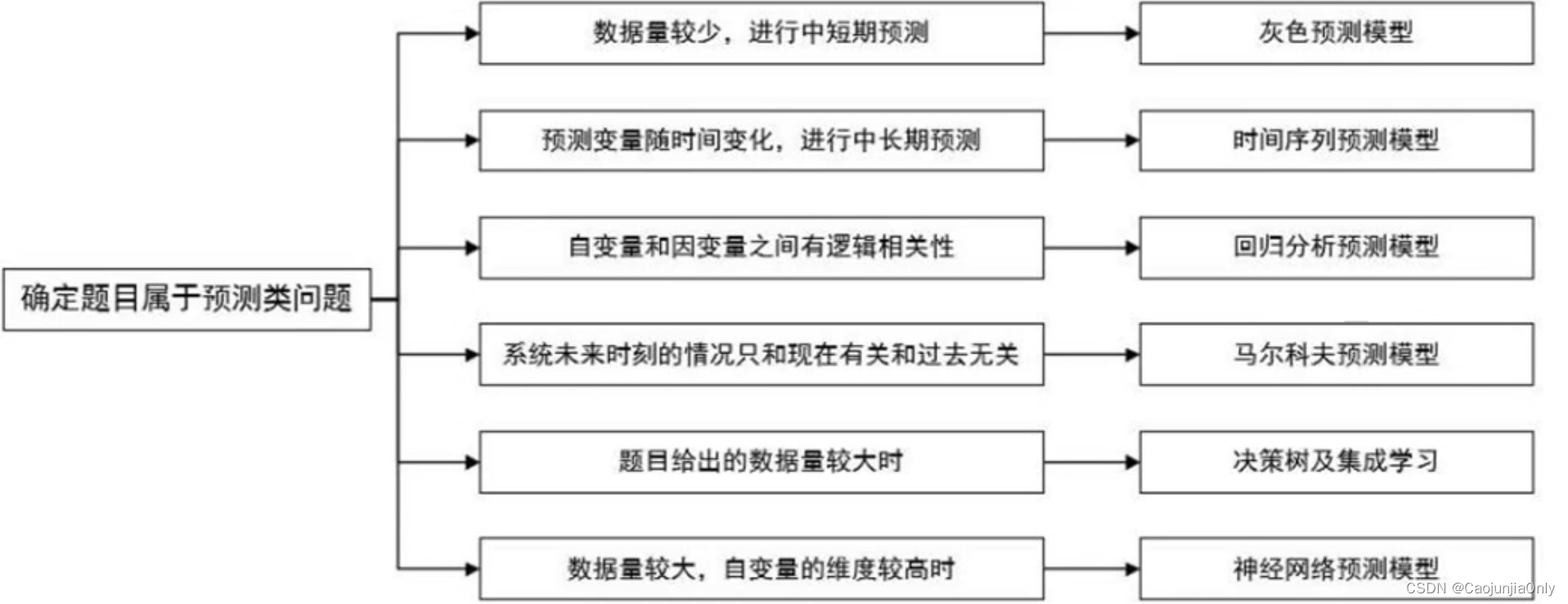
解析常见的预测类算法
灰色预测模型
灰色预测模型是一种利用少量的、不完全的信息,建立数学模型并进行预测的方法。该方法通过对系统行为特征的发展变化规律进行估计预测,同时也可以对行为特征的异常情况发生的时刻进行估计计算,并研究特定时间区间内事件的未来时间分布情况。灰色预测主要使用灰色系统理论中的GM(1,1)模型进行处理。该模型在工业、农业、商业等经济领域,以及环境、社会和军事等领域中都有广泛的应用。它可以根据已有的数据对未来的发展趋势进行预测分析,具有较高的精度和可靠性。

级比检验
级比检验是用来判断原始数据是否满足准指数规律的一种方法。
在灰色预测中,首先需要对原始数据进行级比检验。
级比公式如下,X0表示原始数据。
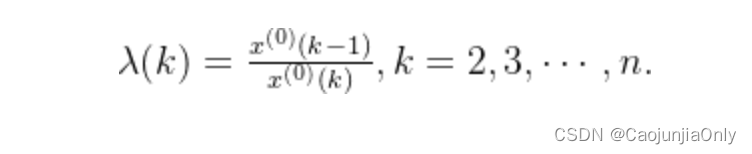
级比检验的目的是判断数据是否满足准指数规律。
在级比检验中,首先需要计算级比,即原始数据与其前一期数据的比值。然后对级比进行统计分析,如计算平均值、方差等。根据级比的统计结果,可以判断数据是否满足准指数规律。如果级比的绝对值接近1,则说明数据满足准指数规律;如果级比的绝对值远离1,则说明数据不满足准指数规律。 级比检验是灰色预测中一个重要的步骤,它可以帮助我们判断数据是否适合进行灰色预测分析。根据级比检验的结果,我们可以选择合适的灰色预测模型进行预测。
x=input('请输入数据');
n=length(x);
jibi = ones(1,n-1);
for i = 2:n
jibi(i-1) = x(i-1)/x(i);
end
max1 = max(jibi);
min1 = min(jibi);
fanwei = exp(2/(n+2))-exp(-2/(n+1))
if max1 - min1 <fanwei
disp(['数据通过级比检验']);
else
disp(['数据不通过级比检验']);
end
灰色预测过程
1.首先生成累加数列。
2.再通过加权邻值生成等权邻值生成数。
3.通过推导可知我们生成的等权邻值生成数满足一定的指数规律,我们的目标就是求出下列灰微分方程中a,b的值:
4.得到灰微分方程后我们就可以对数据进行预测了。
5.最后进行检验,本文用了两种常见的检验方式。

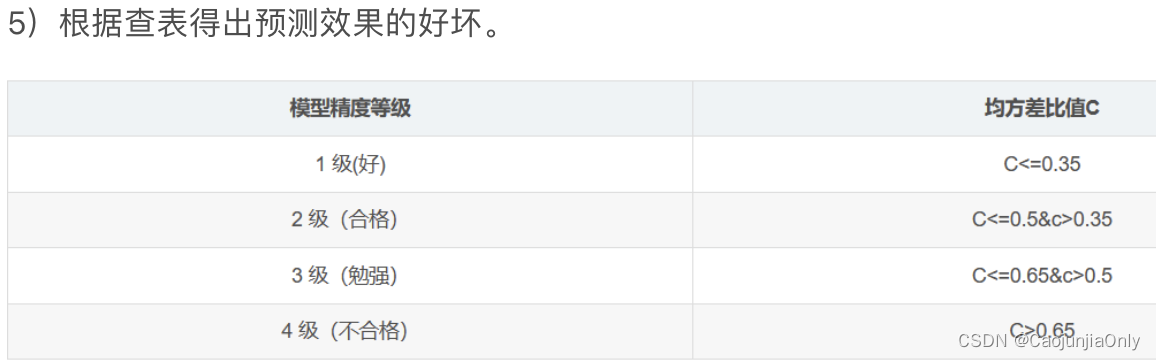
x=input('请输入数据');%x表示原数据
n=length(x);
x1 = ones(1,n);
x1(1)=x(1);
%%生成一次累加数列
for i=2:n
x1(i)=x1(i-1)+x(i)% x1表示累加后的数据
end
z=ones(n-1,2);
%%加权生成数列z
for i=1:(n-1)
z(i,1)=-(x1(i)+x1(i+1))/2;
z(i,2)=1;
end
B=z';
for i=1:(n-1)
x0(i)=x(i+1);%x0表示初始数据的2-n项
end
x0=x0';
U=inv(B*z)*B*x0;
a=U(1);
b=U(2);
t=b/a;
t_test=input('输入需要预测的个数');
i=1:t_test+n;
yucezhi1(i+1)=(x(1)-t).*exp(-a.*i)+t;
yucezhi1(1)=x(1);
yucezhi0 = x(1);
for j=n+t_test:-1:2
yucezhi0(j)=yucezhi1(j)-yucezhi1(j-1);
end
x_init = x;
x=1:n;
xs=2:n+t_test;
yn=yucezhi0(2:n+t_test);
plot(x,x,'^r',xs,yn,'*-b');
% det=0;
% for i=2:n
% det=det+abs(yn(i)-x(i));
% end
% det=det/(n-1);
% disp(['百分绝对误差为:',num2str(det),'%']);
x0 = x0';
%%进行普通的残差检验
for i = 1:n
cancha0(i) = abs((x_init(i)-yucezhi0(i))/x_init(i));
end
cancha_max = max(cancha0);
if cancha_max<0.1
disp(['数据达到较高的要求'])
elseif cancha_max<0.2
disp(['数据达到一般的要求'])
else
disp(['数据不满足要求'])
end
%%进行后验差检验
cancha1(i) = (x_init(i)-yucezhi0(i));
s1 = 0;
s2 = 0;
x_average = sum(x_init)/n;
e_average = sum(cancha1)/n;
for i = i:n
s1 = s1+(x_init(i)-x_average)^2;
s2 = s2+(cancha1(i)-e_average)^2;
end
s1 = s1/n;
s2 = s2/n;
C = s2/s1;
if C<=0.35
disp(['一级,效果好']);
elseif C<=0.5 &C>0.35
disp(['二级,合格']);
elseif C<=0.65 &C>0.5
disp(['三级,勉强']);
else
disp(['四级,不合格']);
end
disp(['预测值为:',num2str(yucezhi0(n+1:n+t_test))]);回归预测方法
回归预测方法包括线性回归、逻辑回归以及其他常见的回归模型。线性回归和逻辑回归通常是人们学习预测模型的第一个算法,而了解更多的学者会知道它们只是所有回归模型的主要两种形式。事实上,回归模型有很多种形式,每种回归都有其特定的适用场合。
在实际应用中,我们可以根据具体需求选择合适的回归模型。除了线性回归和逻辑回归,还有其他常见的回归模型,如多项式回归、岭回归、Lasso回归、弹性网络回归、决策树回归以及随机森林回归等。逐步回归是一种常见的逐步拟合回归模型的方法,通过观察统计值和指标来辨别重要的变量,并逐步增加或删除协变量来优化回归模型。对于有创造力的人来说,也可以根据需要对回归参数进行组合或创造出新的回归模型。但在实际应用中,我们通常会使用最常见的几种回归模型来进行预测和分析。
时间序列分析法
时间序列分析法是一种通过对时间序列中的观察值进行描述和分析来预测未来值或理解序列中的模式和趋势的方法。根据时间序列的不同观察时间,可以是年份、季度、月份或其他任何时间形式。这种方法可以帮助我们了解序列中的趋势、季节性、周期性以及其他可能的影响因素。传统的时间序列分析方法可以将序列中的各个成分分离出来,并通过数学关系式进行分析。这样可以更好地理解序列中的成分之间的关系,并帮助我们做出合理的预测。 时间序列分析法具有简洁、实用的特点,对于利用人力、物力、财力、资源等方面的决策和规划具有很大的帮助。
ARIMA模型
ARIMA模型是一种用于时间序列分析和预测的经典模型。它是由自回归(AR)、移动平均(MA)和差分(I)组成的。ARIMA模型可以用来分析具有一定趋势和季节性的时间序列数据。AR模型是指自回归模型,它用过去观测值的线性组合来预测未来观测值。MA模型是指移动平均模型,它使用白噪声误差的线性组合来预测未来观测值。ARIMA模型可以使用AR、MA或I模型的组合来进行模型配置,以便适应特定的时间序列数据模式。
如果想了解更详细的ARIMA模型的具体内容,可以参考Duke大学的网站,他们提供了关于ARIMA模型的详细解释和应用示例。
在ARIMA模型中,参数值为0可以用来表示不使用该模型的某个部分。这意味着ARIMA模型可以被配置为执行ARMA模型的功能,甚至是简单的AR、I或MA模型。
一旦我们得到了一个平稳的时间序列,下一步就是选择合适的ARIMA模型,也就是模式识别。这一步一般涉及对数据进行模型拟合和参数估计,以及用信息准则来选择最佳模型。通过这些步骤,我们可以得到一个适合时间序列数据的ARIMA模型,从而进行进一步的分析和预测。

AR - 自回归
自回归模型,顾名思义,就是及时地“回顾”过去,分析数据中先前的值,并对它们做出假设。这些先前的值称为“滞后”。一个例子是显示每月铅笔销售的数据。每个月的销售总额将被认为是数据集中的一个“进化变量”。这个模型是作为“利益的演化变量根据其自身的滞后值(即先验值)进行回归”而建立的。
I - 表示综合
与类似的“ARMA”模型相反,ARIMA中的“I”指的是它的综合方面。当应用差分步骤时,数据是“综合”的,以消除非平稳性。表示原始观测值的差异,以允许时间序列变得平稳,即数据值被数据值和以前的值之间的差异替换。
MA - 移动平均线
该模型的移动平均方面,是将观测值与应用于滞后观测值的移动平均模型的残差之间的相关性合并。
ARIMA用于使模型尽可能地符合时间序列数据的特殊形式。
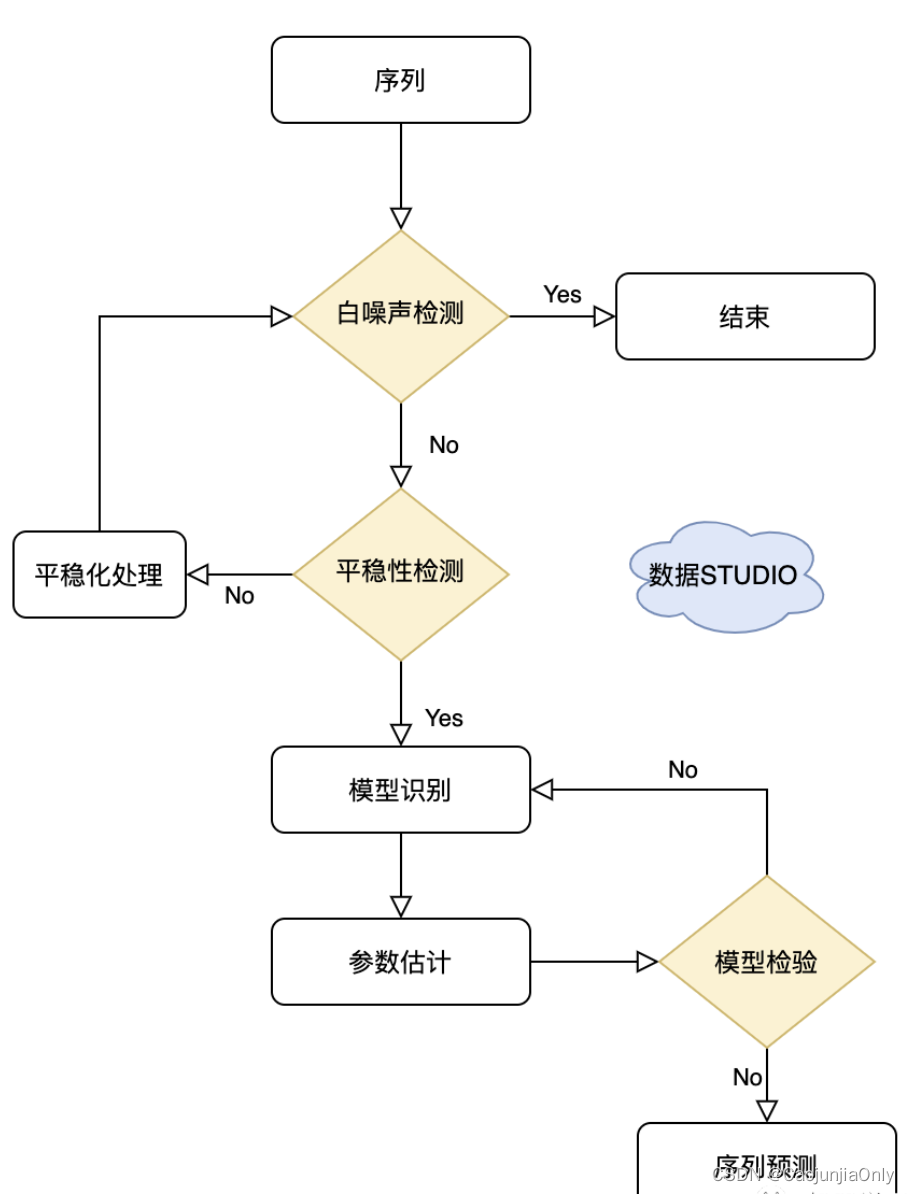
一般步骤
① 首先需要对观测值序列进行平稳性检测,如果不平稳,则对其进行差分运算直到差分后的数据平稳;
② 在数据平稳后则对其进行白噪声检验,白噪声是指零均值常方差的随机平稳序列;
③ 如果是平稳非白噪声序列就计算ACF(自相关系数)、PACF(偏自相关系数),进行ARMA等模型识别;
④ 对已识别好的模型,确定模型参数,最后应用预测并进行误差分析。
微分方程

相关文章:

【数学建模竞赛】预测类赛题常用算法解析
解析常见的预测类算法 灰色预测模型 灰色预测模型是一种利用少量的、不完全的信息,建立数学模型并进行预测的方法。该方法通过对系统行为特征的发展变化规律进行估计预测,同时也可以对行为特征的异常情况发生的时刻进行估计计算,并研究特定…...
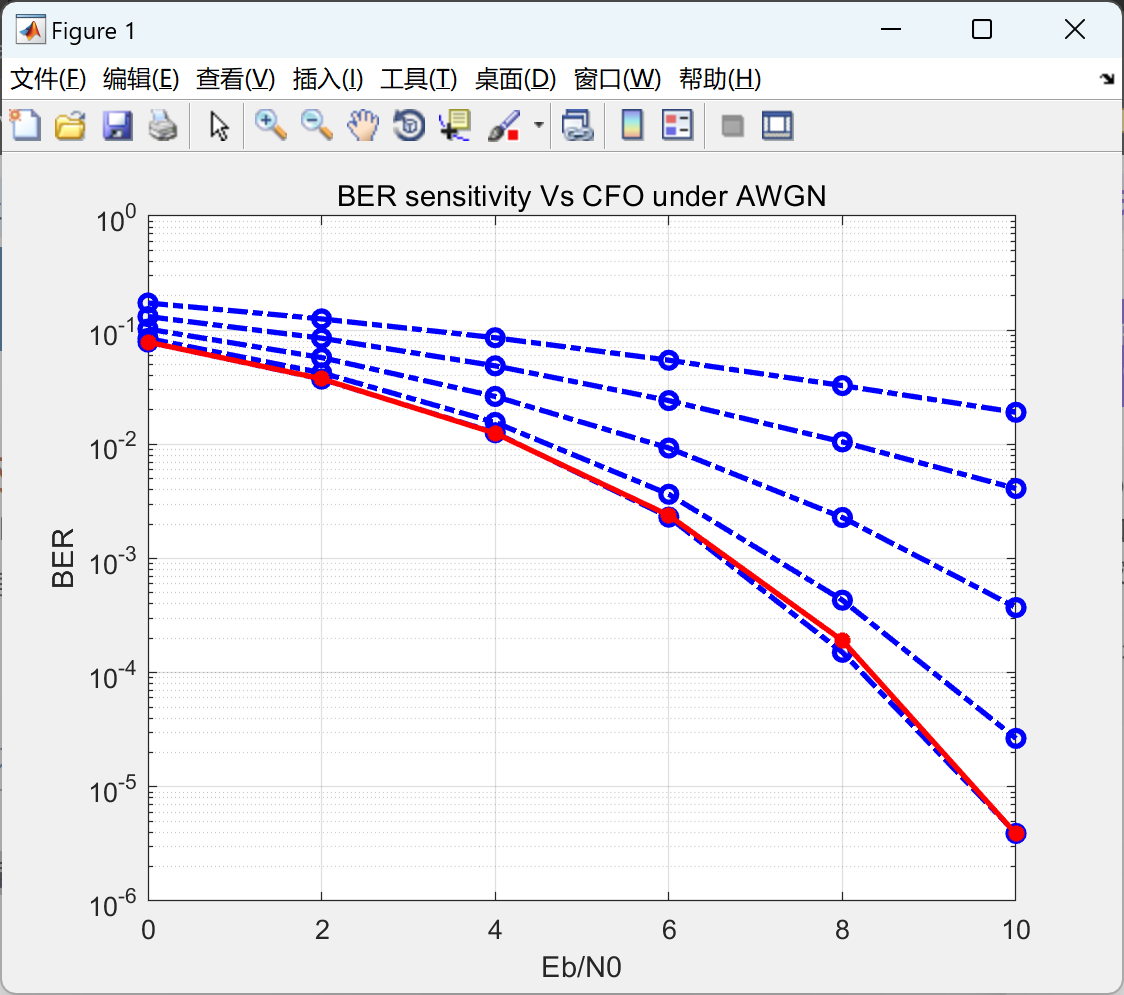
OFDM 系统在 AWGN 信道下对不同载波频率偏移 (CFO) 的 BER 灵敏度研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

go基础07-了解map实现原理并高效使用
对于C程序员出身的Gopher来说,map类型是和切片、interface一样能让他们感受到Go语言先进性的重要语法元素。map类型也是Go语言中最常用的数据类型之一。 go 中 map 怎么表现? 一些有关Go语言的中文教程或译本将map称为字典或哈希表,但在这里…...

SpringMVC进阶:常用注解、参数传递和请求响应以及页面跳转
目录 一、常用注解 1.1.RequestMapping 1.2.RequestParam 1.3.ModelAttribute 1.4.SessionAttributes 1.5.RequestBody 1.6.RequestHeader 1.7.PathVariable 1.8.CookieValue 二、参数传递 2.1.基础类型String 2.2.复杂类型 2.3.RequestParam 2.4.PathVariable 2…...

nacos - centos7.x环境单机与集群快速部署
参考官网:https://nacos.io/zh-cn/docs/what-is-nacos.html 官方集群部署手册:https://nacos.io/zh-cn/docs/cluster-mode-quick-start.html 【单机部署】 1.下载 & 解压到安装目录 下载:wget -c https://github.com/alibaba/nacos/releases/download/2.1.2/nacos-ser…...

文心一言初体验,和ChatGPT语言理解能力比较
文章目录 第一个考验,语义理解第二个考验,历史问题的回答推荐阅读 百度旗下AI大模型文心一言宣布向全社会全面开放,所有用户都可以体验这款AI大模型了。要比较这两个语言模型,我们先设计好题目。 第一个考验,语义理解 题目1&…...
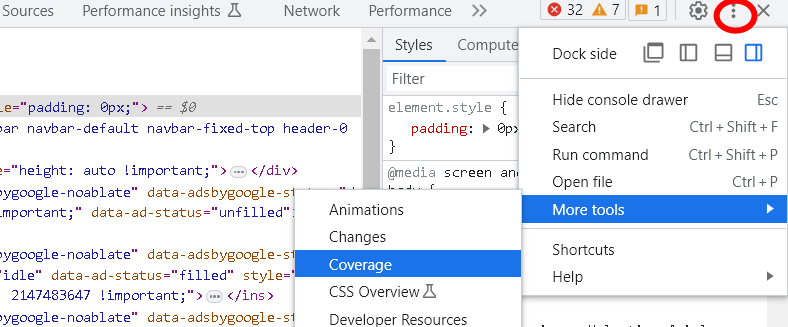
浏览器进程,性能指标,性能优化
目录 浏览器进程:多进程 主进程:显示、交互,增删进程 UI进程:控制地址栏、书签、前进后退 存储进程:cookie,webstorage,indexDB 渲染进程:每个标签页或窗口都有一个独立的渲染进…...

Python基础set集合定义与函数
set集合 集合的特点: 1.集合是无序 2.集合是去重 定义一个空集合 name_set set() 定义一个非空集合 name_set {a, b, c} 关系测试: 交集,并集,差集,对称差集 1.交集:intersection() 或者 & …...
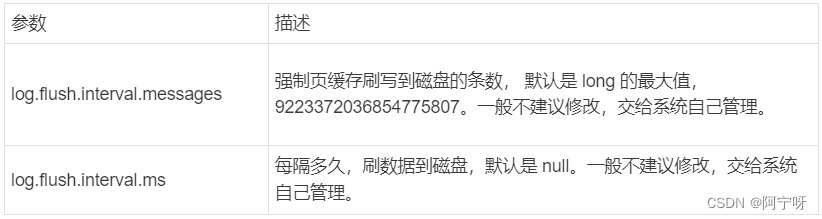
【大数据之Kafka】九、Kafka Broker之文件存储及高效读写数据
1 文件存储 1.1 文件存储机制 Topic是逻辑上的概念,而partition是物理上的概念,每个partition对应于一个log文件,该log文件中存储的是Producer生产的数据。 Producer生产的数据会被不断追加到该log文件末端,为防止log文件过大导致…...

Android 使用Camera2 API 和 GLSurfaceView实现相机预览
GLSurfaceView 和 SurfaceView 是 Android 中用于显示图像的两个视图类,它们在实现方式和使用场景上有一些区别。 实现方式:GLSurfaceView 基于 OpenGL ES 技术实现,可以通过 OpenGL ES 渲染图像。而 SurfaceView 则是通过基于线程的绘制方式…...
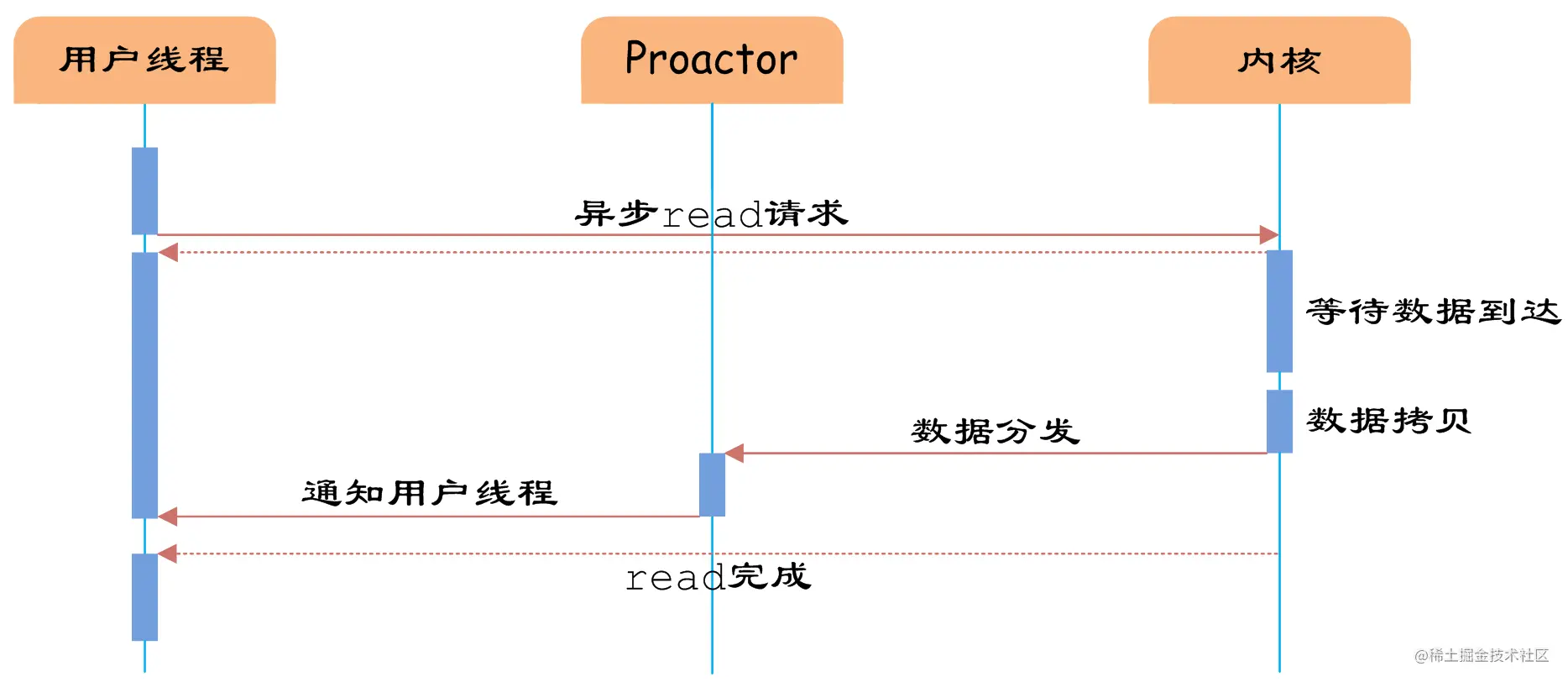
说说IO多路复用
分析&回答 IO多路复用 I/O multiplexing 这里面的 multiplexing 指的其实是在单个线程通过记录跟踪每一个Sock(I/O流)的状态(对应空管塔里面的Fight progress strip槽)来同时管理多个I/O流。直白点说:多路指的是多个socket连接,复用指的是复用一个…...
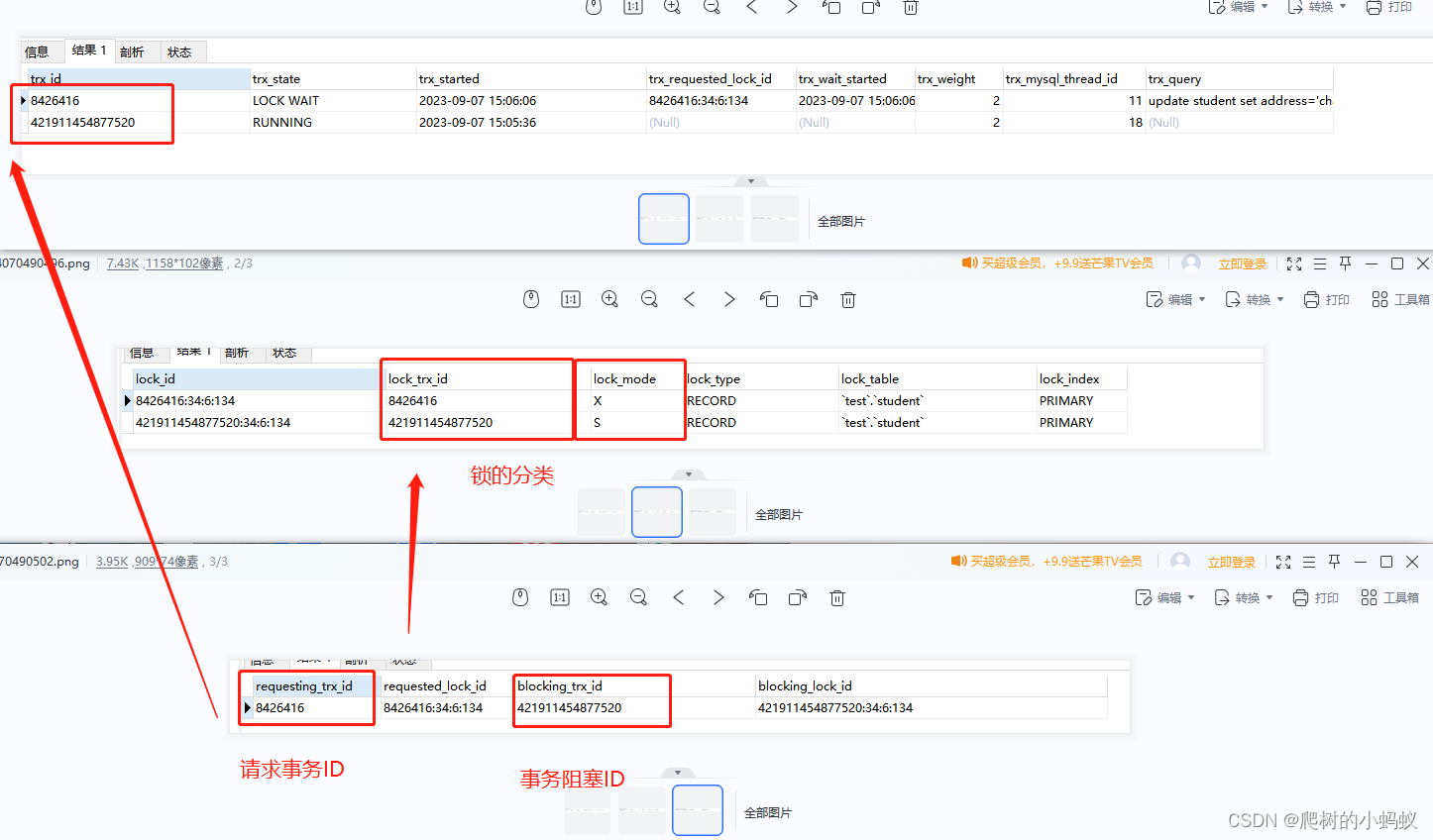
mysql 锁解决的办法
可以查看锁的信息,TRX_MYSQL_THREAD_ID 为processlist的表中的会话id,用于kill select trx_id,trx_state,trx_started,trx_requested_lock_id,trx_wait_started,trx_weight,trx_mysql_thread_id,trx_query from innodb_trx 可以查看锁的模式,类型,锁的表…...
)
C++零碎记录(五)
9. 静态成员 ① 静态成员就是在成员变量和成员函数前加上关键字static,称为静态成员。 ② 静态成员分为: 1. 静态成员变量 --所有对象共享同一份数据 --在编译阶段分配内存 --类内声明,类外初始化 2. 静态成员函数 --所有对象共享同一个函数…...

玩转Mysql系列 - 第16篇:变量详解
这是Mysql系列第16篇。 环境:mysql5.7.25,cmd命令中进行演示。 代码中被[]包含的表示可选,|符号分开的表示可选其一。 我们在使用mysql的过程中,变量也会经常用到,比如查询系统的配置,可以通过查看系统变…...
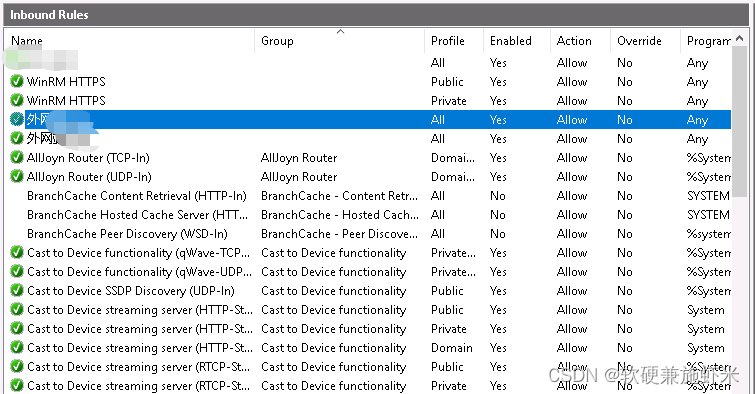
Windows云服务器 PHP搭建网站外网无法访问的问题
前言:本人在华为云上租了一台windows的云主机,可以远程访问桌面的那种,然后想搭个网站,最开始想到的是IIS,测试了下用html的文件,没有问题。但是,php文件却不能用,因为少了PHP环境。…...

TuyaOS Sensor Hub组件介绍
文章目录 Sensor Hub 设计思想分层设计Sensor Hub 层(tdl)Sensor Driver 层(tdd) 传感数据元素类型抽象传感器采集策略 Sensor Hub 对上数据与接口数据结构1. 数据读取的触发模式2. 元素型数据订阅规则3. 数据就绪通知回调4. 传感设备信息 应用接口1. 创建传感器实例2. 启动传感…...

【实战】React17+React Hook+TS4 最佳实践,仿 Jira 企业级项目(总结展望篇)
文章目录 一、项目起航:项目初始化与配置二、React 与 Hook 应用:实现项目列表三、TS 应用:JS神助攻 - 强类型四、JWT、用户认证与异步请求五、CSS 其实很简单 - 用 CSS-in-JS 添加样式六、用户体验优化 - 加载中和错误状态处理七、Hook&…...

Leetcode.321 拼接最大数
题目链接 Leetcode.321 拼接最大数 hard 题目描述 给定长度分别为 m m m 和 n n n 的两个数组,其元素由 0 ∼ 9 0 \sim 9 0∼9 构成,表示两个自然数各位上的数字。现在从这两个数组中选出 k k k ( k ≤ m n ) (k \leq m n) (k≤mn) 个数字拼接成…...

数学建模竞赛常用代码总结-PythonMatlab
数学建模过程中有许多可复用的基础代码,在此对 python 以及 MATLAB 中常用代码进行简单总结,该总结会进行实时更新。 一、文件读取 python (pandas) 文件后缀名(扩展名)并不是必须的,其作用主要一方面是提示系统是用…...
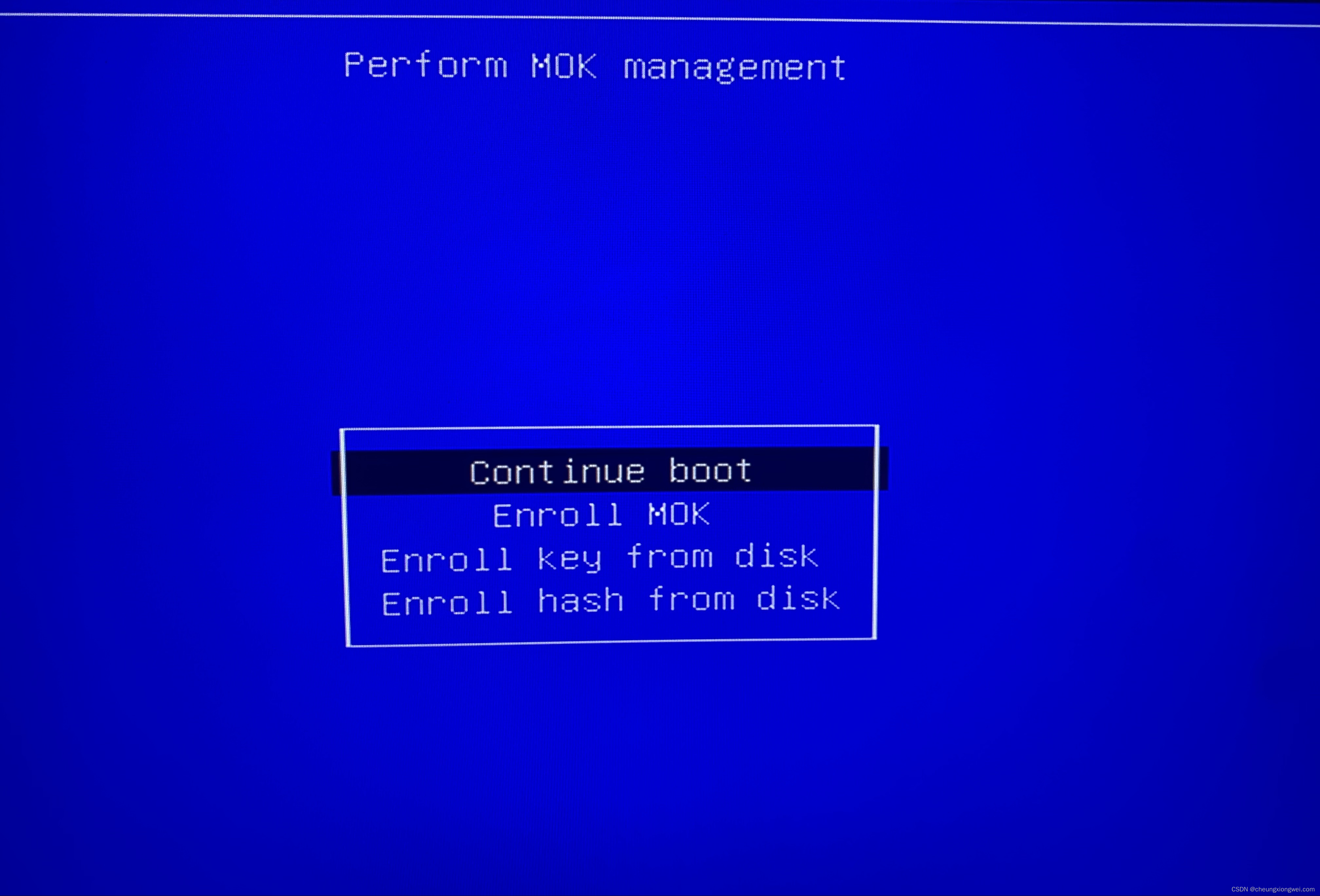
在Ubuntu上安装CUDA和cuDNN以及验证安装步骤
在Ubuntu上安装CUDA和cuDNN以及验证安装步骤 本教程详细介绍了如何在Ubuntu操作系统上安装CUDA(NVIDIA的并行计算平台)和cuDNN(深度神经网络库),以及如何验证安装是否成功。通过按照这些步骤操作,您将能够…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

用鸿蒙HarmonyOS5实现中国象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的中国象棋小游戏的实现代码。这个实现使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chinesechess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├──…...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...

