【群智能算法改进】一种改进的鹈鹕优化算法 IPOA算法[2]【Matlab代码#58】
文章目录
- 【`获取资源`请见文章第5节:资源获取】
- 1. 原始POA算法
- 2. 改进后的IPOA算法
- 2.1 随机对立学习种群初始化
- 2.2 动态权重系数
- 2.3 透镜成像折射方向学习
- 3. 部分代码展示
- 4. 仿真结果展示
- 5. 资源获取
【获取资源请见文章第5节:资源获取】
1. 原始POA算法
此算法详细介绍请参考POA算法介绍
2. 改进后的IPOA算法
2.1 随机对立学习种群初始化
采用随机方法初始化POA种群,生成的种群不均匀,影响了收敛速度和精度。为了获得更好的初始种群,本文采用了随机对立学习策略来进行种群初始:
X i , n e w = ( l + u ) − k X i (1) X_{i,new}=(l+u)-kX_{i}\tag1 Xi,new=(l+u)−kXi(1)
其中, X i X_{i} Xi为原解, X i , n e w X_{i,new} Xi,new为随机对立学习生成的反向解, k k k为[0,1]之间的随机数。
经过随机对立学习策略后,生成了 N N N个反向解,如果反向解的适应度值优于原解,就用反向解替代原解,否则保留原解。
2.2 动态权重系数
基本鹈鹕优化算法的开发阶段,在迭代后期会存在陷入局部最优的情况,使搜索失败。为克服这一弊端,再在其位置更新公式中加入动态权重系数 ω,让它在迭代初期具有较大值,促进全局搜索,迭代后期自适应变小,促进局部搜索并加快收敛速度。
2.3 透镜成像折射方向学习
透镜成像折射反向学习策略的思想来自于凸透镜成像的原理。通过基于当前坐标生成一个反向位置来扩展搜索范围,如图1所示。

在二维坐标中,x轴的搜索范围为(a, b), y轴表示一个凸透镜。假设物体A在x轴上的投影为x,高度为h,通过透镜成像,另一侧的图像为A*, A在x轴上的投影为x,高度为h*。通过以上分析,我们可以得到如下公式:
( a + b ) / 2 − x x ∗ − ( a + b ) / 2 = h h ∗ (2) \frac{(a+b)/2-x}{x^{*}-(a+b)/2 }=\frac{h}{h^{*}} \tag2 x∗−(a+b)/2(a+b)/2−x=h∗h(2)
对公式(2)进行转换,即可得到反向解x*的表达式为:
x ∗ = a + b 2 + a + b 2 k − x k (3) x^{*} =\frac{a+b}{2}+\frac{a+b}{2k}-\frac{x}{k} \tag3 x∗=2a+b+2ka+b−kx(3)
其中, k = h / h ∗ k=h/h^{*} k=h/h∗, a a a和 b b b可以视为某维度的上下限。本文中的 k k k是一个与迭代次数相关的动态自适应值。
3. 部分代码展示
%%
clc
clear
close all%%
Fun_name='F1'; % number of test functions: 'F1' to 'F23'
SearchAgents=30; % number of Pelicans (population members)
Max_iterations=500; % maximum number of iteration
[lb,ub,dim,fobj]=Get_Functions_details(Fun_name); % Object function information
[Best_score_POA,Best_pos_POA,POA_curve]=POA(SearchAgents,Max_iterations,lb,ub,dim,fobj);
[Best_score_SSA,Best_pos_SSA,SSA_curve]=SSA(SearchAgents,Max_iterations,lb,ub,dim,fobj);
[Best_score_WOA,Best_pos_WOA,WOA_curve]=WOA(SearchAgents,Max_iterations,lb,ub,dim,fobj);
[Best_score_GWO,Best_pos_GWO,GWO_curve]=GWO(SearchAgents,Max_iterations,lb,ub,dim,fobj);
[Best_score_IPOA,Best_pos_IPOA,IPOA_curve]=IPOA(SearchAgents,Max_iterations,lb,ub,dim,fobj);%%
figure('Position',[454 445 694 297]);
subplot(1,2,1);
func_plot(Fun_name);
title('Parameter space')
xlabel('x_1');
ylabel('x_2');
zlabel([Fun_name,'( x_1 , x_2 )'])subplot(1,2,2);
t = 1:Max_iterations;
semilogy(t, POA_curve, 'b-', t, SSA_curve, 'k-', t, WOA_curve, 'g-', t, GWO_curve, 'm-', t, IPOA_curve, 'r-','linewidth', 1.5);title(Fun_name)
xlabel('Iteration');
ylabel('Best fitness function');
axis tight
legend('POA','SSA','WOA','GWO','IPOA')display(['The best solution obtained by POA for ' [num2str(Fun_name)],' is : ', num2str(Best_pos_POA)]);
display(['The best optimal value of the objective funciton found by POA for ' [num2str(Fun_name)],' is : ', num2str(Best_score_POA)]);
display(['The best solution obtained by SSA for ' [num2str(Fun_name)],' is : ', num2str(Best_pos_SSA)]);
display(['The best optimal value of the objective funciton found by SSA for ' [num2str(Fun_name)],' is : ', num2str(Best_score_SSA)]);
display(['The best solution obtained by WOA for ' [num2str(Fun_name)],' is : ', num2str(Best_pos_WOA)]);
display(['The best optimal value of the objective funciton found by WOA for ' [num2str(Fun_name)],' is : ', num2str(Best_score_WOA)]);
display(['The best solution obtained by GWO for ' [num2str(Fun_name)],' is : ', num2str(Best_pos_GWO)]);
display(['The best optimal value of the objective funciton found by GWO for ' [num2str(Fun_name)],' is : ', num2str(Best_score_GWO)]);
display(['The best solution obtained by IPOA for ' [num2str(Fun_name)],' is : ', num2str(Best_pos_IPOA)]);
display(['The best optimal value of the objective funciton found by IPOA for ' [num2str(Fun_name)],' is : ', num2str(Best_score_IPOA)]);
4. 仿真结果展示









5. 资源获取
可以获取完整代码资源。
相关文章:

【群智能算法改进】一种改进的鹈鹕优化算法 IPOA算法[2]【Matlab代码#58】
文章目录 【获取资源请见文章第5节:资源获取】1. 原始POA算法2. 改进后的IPOA算法2.1 随机对立学习种群初始化2.2 动态权重系数2.3 透镜成像折射方向学习 3. 部分代码展示4. 仿真结果展示5. 资源获取 【获取资源请见文章第5节:资源获取】 1. 原始POA算法…...

k8s 入门到实战--部署应用到 k8s
k8s 入门到实战 01.png 本文提供视频版: 背景 最近这这段时间更新了一些 k8s 相关的博客和视频,也收到了一些反馈;大概分为这几类: 公司已经经历过服务化改造了,但还未接触过云原生。公司部分应用进行了云原生改造&…...

编程语言新特性:instanceof的改进
以前也写过类似的博文,可能重复。 要判断一个对象是哪个类或父类的实例,JAVA用到instanceof,其实语言也有类似语法。而类一般是多层继承的,有时就让人糊涂。所以我提出改进思路: instanceof:保持不变。ins…...
数据挖掘的学习路径
⭐️⭐️⭐️⭐️⭐️欢迎来到我的博客⭐️⭐️⭐️⭐️⭐️ 🐴作者:秋无之地 🐴简介:CSDN爬虫、后端、大数据领域创作者。目前从事python爬虫、后端和大数据等相关工作,主要擅长领域有:爬虫、后端、大数据…...
逻辑回归Logistic
回归 概念 假设现在有一些数据点,我们用一条直线对这些点进行拟合(这条直线称为最佳拟合直线),这个拟合的过程就叫做回归。进而可以得到对这些点的拟合直线方程。 最后结果用sigmoid函数输出 因此,为了实现 Logisti…...
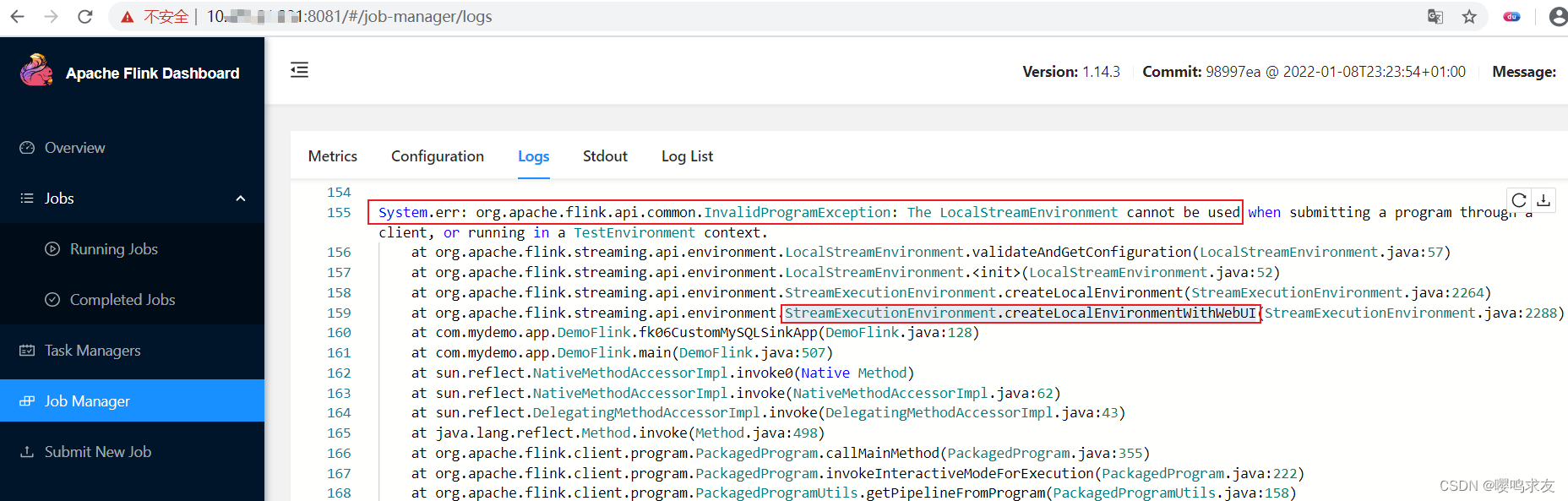
Flink提交jar出现错误RestHandlerException: No jobs included in application.
今天打包一个flink的maven工程为jar,通过flink webUI提交,发现居然报错。 如上图所示,提示错误为: Server Response Message: org.apache.flink.runtime.rest.handler.RestHandlerException: No jobs included in application. …...
】基础概念:数据仓库【用于决策的数据集合】的概念、建立数据仓库的原因与好处)
【数仓基础(一)】基础概念:数据仓库【用于决策的数据集合】的概念、建立数据仓库的原因与好处
文章目录 一. 数据仓库的概念1. 面向主题2. 集成3. 随时间变化4. 非易失粒度 二. 建立数据仓库的原因三. 使用数据仓库的好处 一. 数据仓库的概念 数据仓库的主要作用: 数据仓库概念主要是解决多重数据复制带来的高成本问题。 在没有数据仓库的时代,需…...
电商类面试问题--01Elasticsearch与Mysql数据同步问题
在实现基于关键字的搜索时,首先需要确保MySQL数据库和ES库中的数据是同步的。为了解决这个问题,可以考虑两层方案。 全量同步:全量同步是在服务初始化阶段将MySQL中的数据与ES库中的数据进行全量同步。可以在服务启动时,对ES库进…...
天线材质介绍--FPC天线
...

vue3 的 ref、 toRef 、 toRefs
1、ref: 对原始数据进行拷贝。当修改 ref 响应式数据的时候,模版中引用 ref 响应式数据的视图处会发生改变,但原始数据不会发生改变 <template><div>{{refA}}</div> </template><script lang"ts" setup> impor…...
WebRTC中 setup:actpass、active、passive
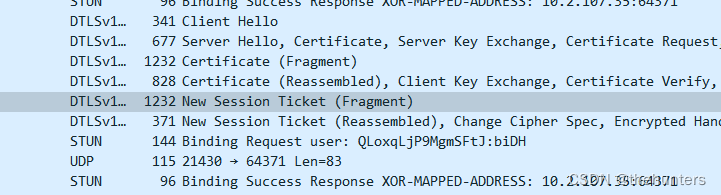
1、先看一下整个DTLS的流程 setup:actpass、active、passive就发生在Offer sdp和Anser SDP中 Offer的SDP是setup:actpass,这个是服务方: v0\r o- 1478416022679383738 2 IN IP4 127.0.0.1\r s-\r t0 0\r agroup:BUNDLE 0 1\r aextmap-allow-mixed\r amsid-semanti…...

ModuleNotFoundError: No module named ‘lavis‘解决方案
大家好,我是爱编程的喵喵。双985硕士毕业,现担任全栈工程师一职,热衷于将数据思维应用到工作与生活中。从事机器学习以及相关的前后端开发工作。曾在阿里云、科大讯飞、CCF等比赛获得多次Top名次。现为CSDN博客专家、人工智能领域优质创作者。喜欢通过博客创作的方式对所学的…...

双指针的问题解法以及常见的leetcode例题。
目录 介绍: 问题1:双指针 剑指offer57 和为S的两个数字。 问题2:剑指Offer 21. 调整数组顺序使奇数位于偶数前面 问题3:连续奇数子串(笔试遇到的真题) 问题4:滑动窗口的最大值 介绍&#…...

python容器模块Collections
Python附带一个模块,它包含许多容器数据类型,名字叫作collections defaultdict defaultdict与dict类型不同,你不需要检查key是否存在,所以我们能这样做: from collections import defaultdict colours ((Yasoob, Y…...
排序算法学习记录-快速排序
快速排序 快速排序关键在于确定一个中间值,使得小于这个中间值的数在左边,大于这个中间值的数在右边。那么中间值该如何确定呢?有以下几种做法 首元素,也就是arr[l]尾元素,也就是arr[r]中间元素,也就是ar…...

安装windows版本的ros2 humble的时候,最后报错
"[rti_connext_dds_cmake_module][warning] RTI Connext DDS environment script not found (\resource\scripts\rtisetenv_x64Win64VS2017.bat). RTI Connext DDS will not be available at runtime, unless you already configured PATH manually." 意思是没找到。…...

Nginx 学习(十)高可用中间件的配置与实现
一 Keepalived热备 1 概述 调度器出现单点故障,如何解决?Keepalived实现了高可用集群Keepalived最初是为LVS设计的,专门监控各服务器节点的状态Keepalived后来加入了VRRP功能,防止单点故障 2 运行原理 Keepalived检测每个服务器节点状…...

[刷题记录]牛客面试笔刷TOP101
牛客笔试算法必刷TOP101系列,每日更新中~ 1.合并有序链表2023.9.3 合并两个排序的链表_牛客题霸_牛客网 (nowcoder.com) 题意大致为: 将两个链表中的元素按照从小到大的顺序合并成为一个链表. 所给予的条件: 给出的所要合并的链表都是从小到大顺序排列的. 思路: 创建一…...

降水预报之双重惩罚
在降水预报中,通常会出现 "双重惩罚问题 "的指标或度量包括那些常用于预报验证的指标或度量。当假阴性(漏报降水事件)和假阳性(误报)受到同等惩罚或加权时,就会出现双重惩罚问题,这在…...
)
一条SQL语句的执行过程(附一次两段式提交)
一条SQL语句的完整执行过程是怎样的呢?我们用select和update语句来举例。 注意在mysql8后,进入服务层后,取消了去查询缓存(属于Server服务层)这个步骤,缓存中key是SQL语句,value是值,这样其实并不会提升性…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...

xmind转换为markdown
文章目录 解锁思维导图新姿势:将XMind转为结构化Markdown 一、认识Xmind结构二、核心转换流程详解1.解压XMind文件(ZIP处理)2.解析JSON数据结构3:递归转换树形结构4:Markdown层级生成逻辑 三、完整代码 解锁思维导图新…...
