9.(Python数模)(分类模型一)K-means聚类
Python实现K-means聚类
K-means原理
K-means均值聚类算法作为最经典也是最基础的无标签分类学习算法。其实质就是根据两个数据点的距离去判断他们是否属于一类,对于一群点,就是类似用几个圆去框定这些点(簇),然后圆心的心就是聚类中心。
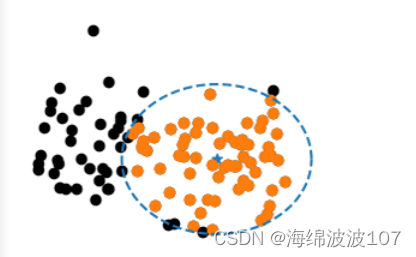
示例一
源代码
from sklearn.cluster import KMeans
import numpy as np# 构造数据样本点集X,并计算K-means聚类
X = np.array([[1, 2], [1, 4], [1, 0], [4, 2], [4, 4], [4, 0]])
kmeans = KMeans(n_clusters=2, random_state=0).fit(X)# 输出及聚类后的每个样本点的标签(即类别),预测新的样本点所属类别
print(kmeans.labels_)
print(kmeans.predict([[0, 0], [4, 4], [2, 1]]))
在这个例子中,KMeans函数的参数意义如下:
n_clusters:表示要创建的聚类数目,这里设置为2,意味着将数据划分为两个簇。
n_init:表示执行算法的次数,每次执行都会随机初始化质心,选择具有最小总误差的结果作为最终模型。这里设置为10,意味着将执行10次算法并选择最好的结果。
random_state:是一个随机数生成器的种子,用于控制随机初始化质心的过程。通过设置相同的种子,可以使得每次运行都得到相同的结果。
.fit(X)表示对数据X执行K均值聚类算法,并训练模型。
运行结果

示例二
源代码
import time
import numpy as np
import matplotlib.pyplot as pltfrom sklearn.cluster import KMeans
from sklearn.metrics.pairwise import pairwise_distances_argmin
from sklearn.datasets._samples_generator import make_blobs# ######################################
# Generate sample data
np.random.seed(0)batch_size = 45
centers = [[1, 1], [-1, -1], [1, -1]]
n_clusters = len(centers)
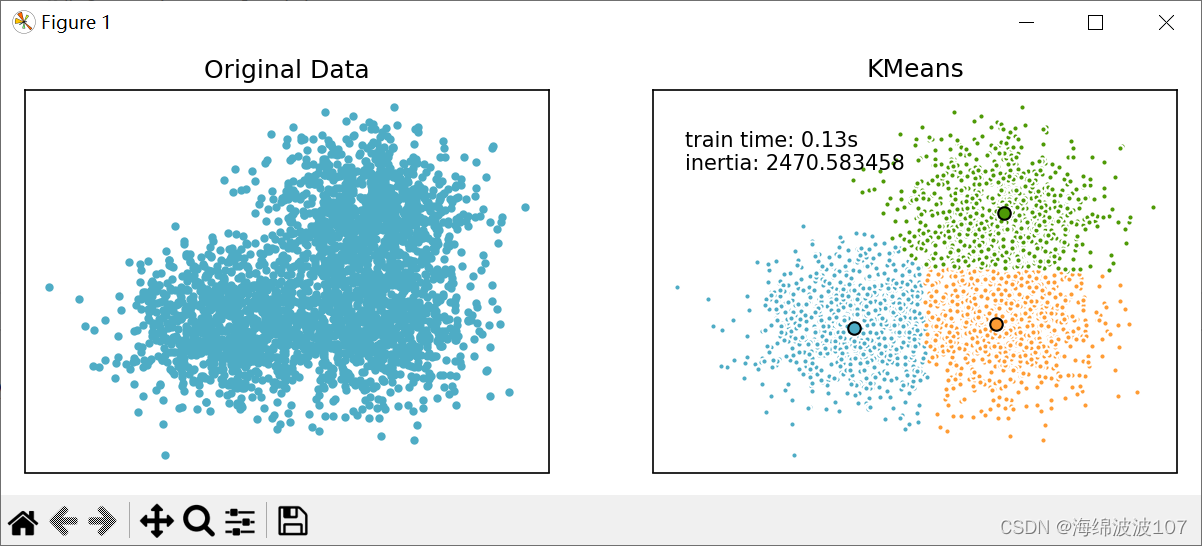
X, labels_true = make_blobs(n_samples=3000, centers=centers, cluster_std=0.7)# plot result
fig = plt.figure(figsize=(8,3))
fig.subplots_adjust(left=0.02, right=0.98, bottom=0.05, top=0.9)
colors = ['#4EACC5', '#FF9C34', '#4E9A06']# original data
ax = fig.add_subplot(1,2,1)
row, _ = np.shape(X)
for i in range(row):ax.plot(X[i, 0], X[i, 1], '#4EACC5', marker='.')ax.set_title('Original Data')
ax.set_xticks(())
ax.set_yticks(())# compute clustering with K-Means
k_means = KMeans(init='k-means++', n_clusters=3, n_init=10)
t0 = time.time()
k_means.fit(X)
t_batch = time.time() - t0k_means_cluster_centers = np.sort(k_means.cluster_centers_, axis=0)
k_means_labels = pairwise_distances_argmin(X, k_means_cluster_centers)# K-means
ax = fig.add_subplot(1, 2, 2)
for k, col in zip(range(n_clusters), colors):my_members = k_means_labels == k # my_members是布尔型的数组(用于筛选同类的点,用不同颜色表示)cluster_center = k_means_cluster_centers[k]ax.plot(X[my_members, 0], X[my_members, 1], 'w',markerfacecolor=col, marker='.') # 将同一类的点表示出来ax.plot(cluster_center[0], cluster_center[1], 'o', markerfacecolor=col,markeredgecolor='k', marker='o') # 将聚类中心单独表示出来
ax.set_title('KMeans')
ax.set_xticks(())
ax.set_yticks(())
plt.text(-3.5, 1.8, 'train time: %.2fs\ninertia: %f' % (t_batch, k_means.inertia_))plt.show()
运行结果
代码注释
1、使用Scikit-learn库中的make_blobs函数来生成随机的高斯分布数据集。通过指定n_samples参数为3000,centers参数为所需的中心点数量,cluster_std参数为0.7来生成数据集。返回数据点和对应的标签列表。
数据点列表

标签列表
2、fig.subplots_adjust(left=0.02, right=0.98, bottom=0.05, top=0.9)这段代码用于调整子图的位置。它通过设置左边界、右边界、底边界和顶边界的值来控制子图的位置。在这个例子中,左边界被设置为0.02,右边界被设置为0.98,底边界被设置为0.05,顶边界被设置为0.9。这意味着子图将占据整个画布的宽度的96%(从左边界到右边界),并且在垂直方向上从底边界的5%位置开始,到顶边界的90%位置结束。通过调整这些值,你可以改变子图在画布上的位置和大小。
3、ax = fig.add_subplot(1,2,1)这是在 Python 中创建一个简单的单图形对象,使用 matplotlib 库中的 fig.add_subplot() 方法。它创建了一个包含一个子图的图形。子图是位置在 (1,1) 的唯一子图。该变量 b’ax’ 将该子图对象存储起来,以便可以使用它来设置图形属性和添加绘图元素。
4、k_means = KMeans(init=‘k-means++’, n_clusters=3, n_init=10)。K-Means是一种常用的无监督学习算法,用于将数据划分为预先指定数量的簇(clusters)。在代码中,参数init='k-means’指定了用K-Means算法初始化聚类中心,初始化的方法有三种:k-means++,random,或者是一个数组。
k-means++能智能的选择初始聚类中心进行k均值聚类,加快收敛速度。该示例中初始化了聚类中心[[1, 1], [-1, -1], [1, -1]],选择K-means++加快收敛。random则是从数据中随机的选择k个观测值作为初始的聚类中心。
n_clusters=3指定了要生成的簇的数量为3,n_init=10指定了进行不同初始值运行的次数,以选择最佳的聚类结果。
对比
使用k-means++方法

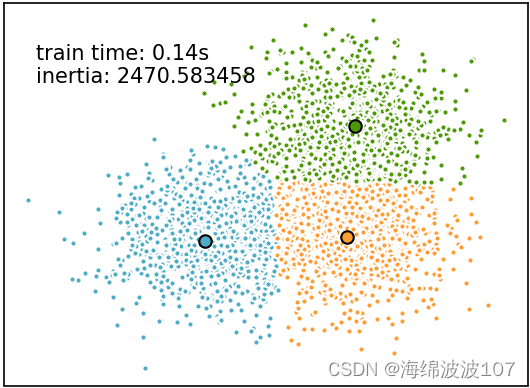
使用random方法的3个聚类中心

运算时间为0.14s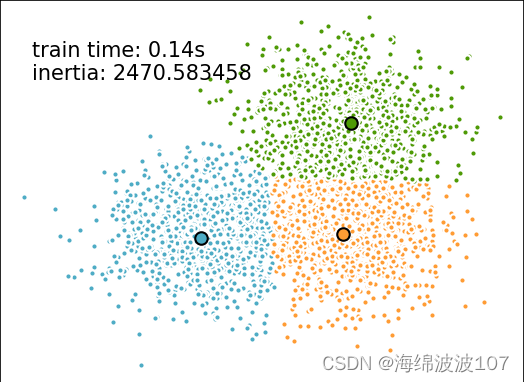
两种方法总内部方差一样,运算时间也一样,当更换为更大的数据时30000样本时,在相同运算时间下,k-means++计算的总内部方差更小,收敛效果更好。
5、k_means.fit(X)。使用了k-means算法的fit()方法来拟合数据集X。
6、k_means_cluster_centers = np.sort(k_means.cluster_centers_, axis=0)。在这段代码中,k_means是聚类模型,k_means.cluster_centers_是获取聚类中心的属性,np.sort是对聚类中心进行排序的函数,axis=0表示按照列的顺序进行排序。最后,k_means_cluster_centers存储了排序后的聚类中心。
聚类中心的属性如下:

排序后结果如下:

7、k_means_labels = pairwise_distances_argmin(X, k_means_cluster_centers)pairwise_distances_argmin()是一个函数,它根据输入的数据点X和K-means聚类算法的中心点k_means_cluster_centers,计算每个数据点最近的中心点,并返回对应的标签。换句话说,它会将数据点分配到最近的簇中,并返回每个数据点所属的簇标签。
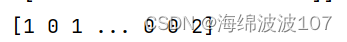
8、my_members = k_means_labels == k
得到一个布尔值列表,用于下面索引选出不同的类
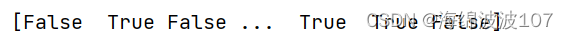
参考博文
Python学习——K-means聚类
一文速学数模-聚类模型(一)K-means聚类算法详解+Python代码实例
相关文章:
9.(Python数模)(分类模型一)K-means聚类
Python实现K-means聚类 K-means原理 K-means均值聚类算法作为最经典也是最基础的无标签分类学习算法。其实质就是根据两个数据点的距离去判断他们是否属于一类,对于一群点,就是类似用几个圆去框定这些点(簇),然后圆心…...
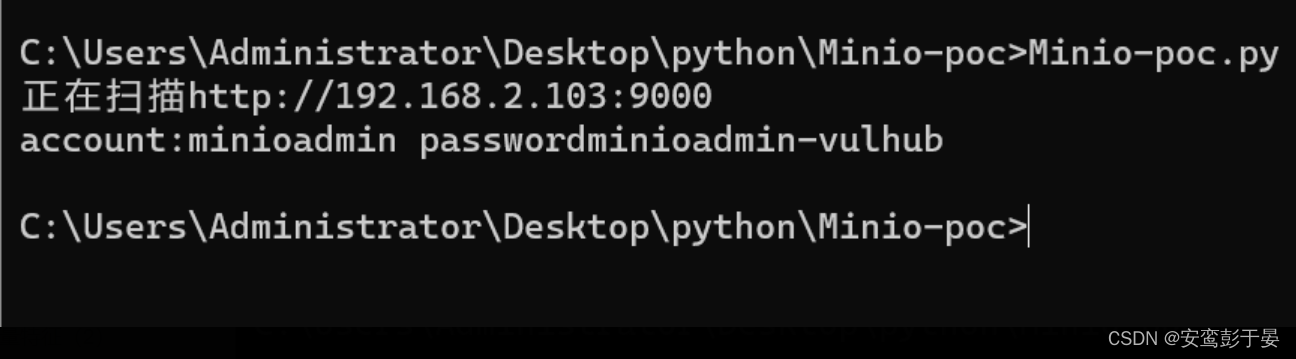
MinIO集群模式信息泄露漏洞(CVE-2023-28432)
前言:MinIO是一个用Golang开发的基于Apache License v2.0开源协议的对象存储服务。虽然轻量,却拥有着不错的性能。它兼容亚马逊S3云存储服务接口,非常适合于存储大容量非结构化的数据。该漏洞会在前台泄露用户的账户和密码。 0x00 环境配置 …...

【从零单排Golang】第十五话:用sync.Once实现懒加载的用法和坑点
在使用Golang做后端开发的工程中,我们通常需要声明一些一些配置类或服务单例等在业务逻辑层面较为底层的实例。为了节省内存或是冷启动开销,我们通常采用lazy-load懒加载的方式去初始化这些实例。初始化单例这个行为是一个非常经典的并发处理的案例&…...
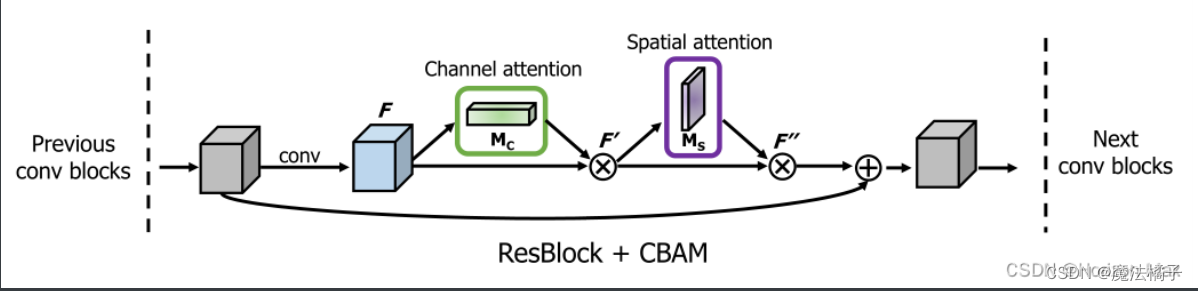
常见注意力机制
注意力机制 (具有自适应性) 18年提出的一种新的 卷积注意力模块 ;对前馈卷积神经网络 是一个 简单而有效的 注意力模块 ; 因为它的 轻量级和通用性 ,可以 无缝集成到任何CNN网络 当中, 对我们来讲&…...
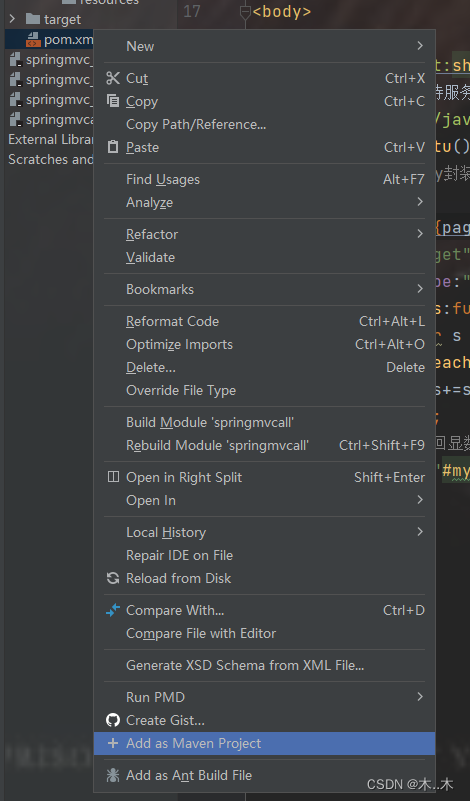
解决报错之org.aspectj.lang不存在
一、IDEA在使用时,可能会遇到maven依赖包明明存在,但是build或者启动时,报找不存在。 解决办法:第一时间检查Setting->Maven-Runner红圈中的√有没有选上。 二、有时候,明明依赖包存在,但是Maven页签中…...

java之SpringBoot基础篇、前后端项目、MyBatisPlus、MySQL、vue、elementUi
文章目录 前言JC-1.快速上手SpringBootJC-1-1.SpringBoot入门程序制作(一)JC-1-2.SpringBoot入门程序制作(二)JC-1-3.SpringBoot入门程序制作(三)JC-1-4.SpringBoot入门程序制作(四)…...

golang中如何判断字符串是否包含另一字符串
golang中如何判断字符串是否包含另一字符串 在Go语言中,可以使用strings.Contains()函数来判断一个字符串是否包含另一个字符串。该函数接受两个参数:要搜索的字符串和要查找的子字符串,如果子字符串存在于要搜索的字符串中,则返…...

ONNX OpenVino TensorRT MediaPipe NCNN Diffusers ComfyUI
框架 和Java生成的中间文件可以在JVM上运行一样,AI技术在具体落地应用方面,和其他软件技术一样,也需要具体的部署和实施的。既然要做部署,那就会有不同平台设备上的各种不同的部署方法和相关的部署架构工具 onnx 在训练模型时可以…...
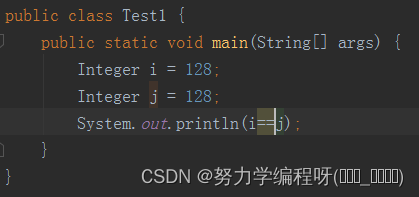
java中使用 Integer 和 int 的 含义、使用方法 及之间的区别
学习目标: 学习目标如下: 明确 Integer 和 int 的 含义、使用方法 及之间的区别 学习内容: 一、区别: 1.Integer是int的包装类,int则是java的一种基本的数据类型; 2.Integer变量必须实例化之后才能使用&a…...

点云从入门到精通技术详解100篇-点云的特征检测
目录 前言 点云配准的研究背景 多元时间序列的相似性分析研究背景及意义 国内外研究现状...

DOM破坏绕过XSSfilter例题
目录 一、什么是DOM破坏 二、例题1 编辑 三、多层关系 1.Collection集合方式 2.标签关系 四、例题2 一、什么是DOM破坏 DOM破坏(DOM Clobbering)指的是对网页上的DOM结构进行不当的修改,导致页面行为异常、性能问题、安全风险或其他不…...

代码随想录Day_56打卡
①、两个字符串的删除操作 给定两个单词 word1 和 word2 ,返回使得 word1 和 word2 相同所需的最小步数。 每步 可以删除任意一个字符串中的一个字符。 事例: 输入: word1 "sea", word2 "eat" 输出: 2 解释: 第一步将 "sea&…...

高忆管理:六连板捷荣技术或难扛“华为概念股”大旗
在本钱商场上名不见经传的捷荣技术(002855.SZ)正扛起“华为概念股”大旗。 9月6日,捷荣技术已拿下第六个连续涨停板,短短七个生意日,股价累积涨幅逾越90%。公司已连发两份股票生意异动公告。 是炒作,还是…...
「解析」YOLOv5 classify分类模板
学习深度学习有些时间了,相信很多小伙伴都已经接触 图像分类、目标检测甚至图像分割(语义分割)等算法了,相信大部分小伙伴都是从分类入门,接触各式各样的 Backbone算法开启自己的炼丹之路。 但是炼丹并非全是 Backbone,更多的是各…...
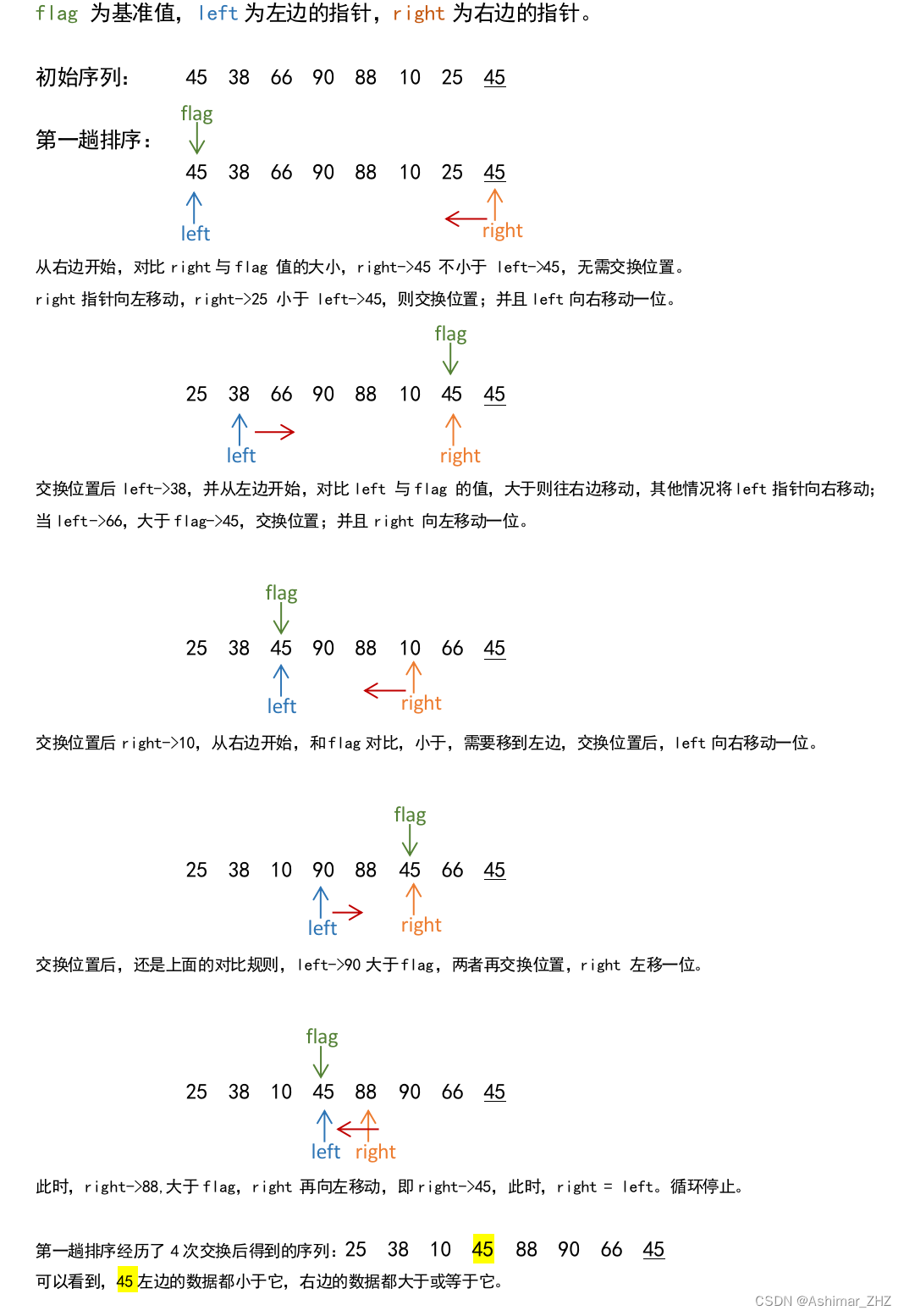
交换排序——冒泡排序、快速排序
交换排序就是通过比较交换实现排序。分冒泡排序和快速排序两种。 一、冒泡排序: 1、简述 顾名思义就是大的就冒头,换位置。 通过多次重复比较、交换相邻记录而实现排序;每一趟的效果都是将当前键值最大的记录换到最后。 冒泡排序算法的原…...

Android 10.0 禁用adb shell input输入功能
1.前言 在10.0的产品开发中,在进行一些定制开发中,对于一些adb shell功能需要通过属性来控制禁止使用input 等输入功能,比如adb shell input keyevent 响应输入事件等,所以就需要 熟悉adb shell input的输入事件流程,然后来禁用adb shell input的输入事件功能,接下来分…...
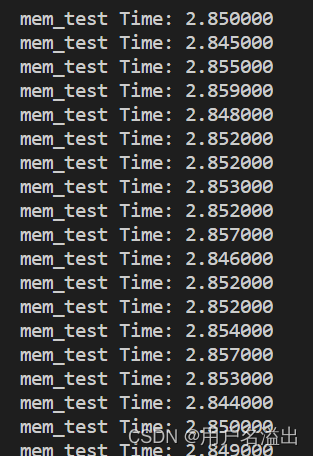
cuda显存访问耗时
背景: 项目中有个数据量大小为5195 * 512 * 128float 1.268G的显存,发现有个函数调用很耗时,函数里面就是对这个显存进行128个元素求和,得到一个5195 * 512的图像 分析 1. 为什么耗时 直观上感觉这个流程应该不怎么耗时才对&a…...
【HTML5高级第三篇】drag拖拽、音频视频、defer/async属性、dialog应用
文章目录 一、拖拽事件1.1 拖拽事件1.2 案例:拖拽丢弃图片 二、音频和视频三、defer 与 async 属性3.1 概述3.2 示例一:3.3 示例二: 四、dialog 元素 一、拖拽事件 原生JavaScipt案例合集 JavaScript DOM基础 JavaScript 基础到高级 Canvas…...

独享IP vs. 共享IP:哪种更适合你?
无论是个人用户还是企业组织,在互联网上都需要一个唯一标识来与其他设备进行通信。这就涉及到使用独立分配给自己或多个用户分享的公共 IP 地址(也称为共享 IP)。那么,究竟应该选择独占一个专用地址还是与他人分享相同地址呢&…...

【Arduino27】DHT11温湿度传感器模拟值实验
硬件准备 DHT11温湿度:1个 面包板:1个 杜邦线:3根 硬件连线 VDD引脚接 5V 电源 DATE引脚接 4号 接口 GND引脚接 GND 接口 软件程序 #include<DHT.h>#define DHT11_pin 4 //温湿度传感器引脚DHT dht(DHT11_pin,DHT11);float tem…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...
