数据结构和算法(2):向量
抽象数据类型

数组到向量
C/C++ 中,数组A[]中的元素与[0,n)内的编号一一对应,A[0],A[1],...,A[n-1];反之,每个元素均由(非负)编号唯一指代,并可直接访问A[i] 的物理地址 = A+i × s,s 为单个元素占用的空间量,所以也叫作线性数组。
向量是数组的抽象与泛化,由一组元素按线性次数封装而成。各元素与[0,n)内的秩(rank)一一对应。
元素的类型不限于基本类型;
操作、管理维护更加简化、统一与安全;
可更为便捷地参与复杂数据结构的定制与实现

Vector 模板类
using Rank = unsigned int; //秩
#define DEFAULT_CAPACITY 3 //默认的初始容量(实际应用中可设置为更大)
template <typename T> class Vector { //向量模板类
private:Rank_size;int_capacity;T* _elem;//规模、容量、数据区
protected:/.../
public://构造函数Vector ( Rank c = DEFAULT_CAPACITY, Rank s = 0, T v = 0 ) //容量为c、规模为s、所有元素初始为v{ _elem = new T[_capacity = c]; for ( _size = 0; _size < s; _elem[_size++] = v ); } //s<=cVector ( T const* A, Rank n ) { copyFrom ( A, 0, n ); } //数组整体复制Vector ( T const* A, Rank lo, Rank hi ) { copyFrom ( A, lo, hi ); } //区间Vector ( Vector<T> const& V ) { copyFrom ( V._elem, 0, V._size ); } //向量整体复制Vector ( Vector<T> const& V, Rank lo, Rank hi ) { copyFrom ( V._elem, lo, hi ); } //区间// 析构函数~Vector() { delete [] _elem; } //释放内部空间
}; //Vector
可扩充向量
静态空间管理
开辟内部数组_elem[]并使用一段地址连续的物理空间
_capacity :总容量
_size:当前的实际规模n
若采用静态空间管理策略,容量_capacity固定,则有明显的不足
1.上溢( overf1ow ) : _elem[]不足以存放所有元素
尽管此时系统仍有足够的空间
2.下溢( underflow ) : _elem[]中的元素寥寥无几
装填因子(load factor) λ = _ s i z e / _ c a p a c i t y < < 50 % \lambda = \_size/\_capacity << 50\% λ=_size/_capacity<<50%
更糟糕的是,一般的应用环境中难以准确预测空间的需求量。
动态空间管理
在即将发生上溢时,适当地扩大内部数组的容量
template <typename T>
void Vector<T>::expand() { //向量空间不足时扩容if(_size < _capacity) return; //尚未满员时,不必扩容_capacity = max(_capacity, DEFAULT_CAPACITY); //不低于最小容量T* oldElem =_elem; _elem = new T[_capacity <<= 1];//容量加倍for (int i = 0; i <_size; i++) //复制原向量内容_elem[i] = oldElem[i]; //T为基本类型,或已重载赋值操作符'='delete [] oldElem; //释放原空间
}
得益于向量的封装,尽管扩容之后数据区的物理地址有所改变,却不致出现野指针。
容量加倍策略在时间复杂度上总体优于容量递增策略。
| \space | 递增策略 | 倍增策略 |
|---|---|---|
| 累计增容时间 | O ( n 2 ) \mathcal O(n^2) O(n2) | O ( n ) \mathcal O(n) O(n) |
| 分摊增容时间 | O ( n ) \mathcal O(n) O(n) | O ( 1 ) \mathcal O(1) O(1) |
| 装填因子 | ≈ 100 % ≈100\% ≈100% | > 50 % >50\% >50% |
平均分析 vs 分摊分析
平均复杂度或期望复杂度(average/expected complexity)
根据数据结构各种操作出现概率的分布,将对应的成本加权平均
各种可能的操作,作为独立事件分别考查
割裂了操作之间的相关性和连贯性
往往不能准确地评判数据结构和算法的真实性能
分摊复杂度(amortized complexity)
对数据结构连续地实施足够多次操作,所需总体成本分摊至单次操作
从实际可行的角度,对一系列操作做整体的考量
更加忠实地刻画了可能出现的操作序列
可以更为精准地评判数据结构和算法的真实性能
分摊复杂度和平均复杂度的结果并没有必然联系。
无序向量
元素访问
通过V.get(r)和V.put(r)接口,可以对元素进行读写。
可以重载下标操作符,增加其便捷性:
template<typename T> //0 <= _size
T & Vector<T>::operator[](Rank(r)) const {return _elem[r];}
此后,对外的V[r]即对应内部的V._elem[r]可以使用下标进行操作:
//右值
T x = V[r] + U[s] + W[t];
//左值
V[r] = T(2*x + 3);
插入
template <typename T> //将e插入至[r]
Rank Vector<T>::insert ( Rank r, T const& e ) { //0 <= r <= sizeexpand(); //如必要,先扩容for ( Rank i = _size; r < i; i-- ) //自后向前,后继元素_elem[i] = _elem[i-1]; //顺次后移一个单元_elem[r] = e; _size++; //置入新元素并更新容量return r; //返回秩
}
区间删除
template <typename T> int Vector<T>::remove( Rank lo, Rank hi ) { //0 <= lo <= hi <= nif ( lo == hi ) return 0; //出于效率考虑,单独处理退化情况while ( hi < _size ) _elem[lo++] = _elem[hi++]; //后缀[hi, _size)顺次前移 hi-lo 位_size = lo; shrink(); //更新规模,lo=_size之后的内容无需清零;如必要,则缩容//若有必要,则缩容return hi-lo;//返回被删除元素的数目
}
单元素删除
可以视作区间删除的特例:[r] = [r,r+1)
template <typename T> T Vector<T>::remove( Rank r ) { //删除向量中秩为r的元素,0 <= r < sizeT e = _elem[r]; //备份被删除元素remove( r, r + 1 ); //调用区间删除算法,等效于对区间[r, r + 1)的删除return e; //返回被删除元素
}
查找
template <typename T> //在无序向量中顺序查找e:成功则返回最靠后的出现位置,否则返回lo-1
Rank Vector<T>::find ( T const& e, Rank lo, Rank hi ) const { //0 <= lo < hi <= _sizewhile ( ( lo < hi-- ) && ( e != _elem[hi] ) ); //从后向前,顺序查找return hi; //若hi < lo,则意味着失败;否则hi即命中元素的秩
}
输入敏感:最好: O ( 1 ) \mathcal O(1) O(1) ; 最差: O ( n ) \mathcal O(n) O(n)
实例:去重(删除重复元素)
template <typename T> Rank Vector<T>::dedup() { //删除无序向量中重复元素(高效版)Rank oldSize = _size; //记录原规模for ( Rank i = 1; i < _size; ) //自前向后逐个考查_elem[1,_size)if ( -1 == find(_elem[i], 0, i) ) //在前缀[0,i)中寻找与[i]雷同者(至多一个),O(i)i++; //若无雷同,则继续考查其后继elseremove(i); //否则删除[i],O(_size-i)return oldSize - _size; //被删除元素总数
}
每轮迭代中 find() 和 remove(累计耗费线性时间,总体为 O ( n 2 ) \mathcal O(n^2) O(n2) )
有序向量:唯一化
有序/无序序列中,任意/总有一对相邻元素顺序/逆序因此,相邻逆序对的数目,可用以度量向量的逆序程度。
实例:有序向量去重
观察︰在有序向量中,重复的元素必然相互紧邻构成一个区间。因此,每一区间只需保留单个元素即可
低效算法
template <typename T> Rank Vector<T>::uniquify() { //有序向量重复元素剔除算法(低效版)Rank oldSize = _size, i = 1; //当前比对元素的秩,起始于首元素while ( i < _size ) //从前向后,逐一比对各对相邻元素_elem[i - 1] == _elem[i] ? remove ( i ) : i++; //若雷同,则删除后者;否则,转至后一元素return oldSize - _size; //向量规模变化量,即被删除元素总数
}
效率低,运行时间主要取决于 while 循环,次数共计:_size - 1 = n -1
最坏: O ( n 2 ) \mathcal O(n^2) O(n2)
高效算法
反思:低效的根源狂于,同一元素可作为被删除元素的后继多次前移
启示︰若能以重复区间为单位,成批删除雷同元素,性能必将改进
template <typename T> Rank Vector<T>::uniquify() { //有序向量重复元素剔除算法(高效版)Rank i = 0, j = 0; //各对互异“相邻”元素的秩while ( ++j < _size ) //逐一扫描,直至末元素if ( _elem[i] != _elem[j] ) //跳过雷同者_elem[++i] = _elem[j]; //发现不同元素时,向前移至紧邻于前者右侧_size = ++i; shrink(); //直接截除尾部多余元素return j - i; //向量规模变化量,即被删除元素总数
}
共计 n - 1 次迭代,每次常数时间,累计 O ( n ) \mathcal O(n) O(n) 时间。
有序向量:二分查找(A)
//二分查找算法(版本A)︰在有序向量的区间[lo,hi)内查找元素e,0 <= lo <= hi <= _size
template <typename T> static Rank binSearch( T* S, T const& e, Rank lo,Rank hi ) {while ( lo < hi ) { //每步迭代可能要做两次比较判断,有三个分支Rank mi = ( lo + hi ) >>1; //以中点为轴点(区间宽度折半,等效于其数值表示的右移一位)if( e < s[mi] ) hi = mi; //深入前半 段[ 1o, mi)继续查找else if ( S[mi] < e ) lo = mi + 1; //深入后半段(mi,hi)继续查找elsereturn mi; //在mi处命中} //成功查找可以提前终止return -1; //查找失败
} //有多个命中元素时,不能保证返回秩最大者;查找失败时,简单地返回-1,而不能指示失败的位置
转向左、右分支前的关键码比较次数不等,而递归深度却相同
有序向量:Fib 查找
若能通过递归深度的不均衡,对转向成本的不均衡进行补偿平均查找长度应能进一步缩短…
#include "fibonacci/Fib.h" //引入Fib数列类
//Fibonacci查找算法(版本A):在有序向量的区间[lo, hi)内查找元素e,0 <= lo <= hi <= _size
template <typename T> static Rank fibSearch( T* S, T const& e, Rank lo, Rank hi ) {//用O(log_phi(n = hi - lo)时间创建Fib数列for ( Fib fib( hi - lo ); lo < hi; ) { //Fib制表备查;此后每步迭代仅一次比较、两个分支while ( hi - lo < fib.get() ) fib.prev(); //自后向前顺序查找(分摊O(1))Rank mi = lo + fib.get() - 1; //确定形如Fib(k)-1的轴点if ( e < S[mi] ) hi = mi; //深入前半段[lo, mi)继续查找else if ( S[mi] < e ) lo = mi + 1; //深入后半段(mi, hi)继续查找else return mi; //在mi处命中} //一旦找到,随即终止return -1; //查找失败
} //有多个命中元素时,不能保证返回秩最大者;失败时,简单地返回-1,而不能指示失败的位置
通用策略:对于任何的 A [ 0 , n ) A[0,n) A[0,n),总是选取 A [ λ n ] A[\lambda n] A[λn] 作为轴点, 0 ≤ λ < 1 0\leq \lambda<1 0≤λ<1
在 [ 0 , 1 ) [0,1) [0,1)内, λ \lambda λ 如何取值才能达到最优 ? 设平均查找长度为 α ( λ ) ⋅ l o g 2 n α(\lambda)· log_2n α(λ)⋅log2n,何时 α ( λ ) α(\lambda) α(λ) 最小?
二分查找: λ = 0.5 \lambda = 0.5 λ=0.5 Fib 查找: 0.6180339... 0.6180339... 0.6180339...
有序向量:二分查找(B)
二分查找中左、右分支转向代价不平衡的问题,也可直接解决。将中间点包含在了右边。
//二分查找算法(版本B):在有序向量的区间[lo, hi)内查找元素e,0 <= lo < hi <= _size
template <typename T> static Rank binSearch( T* S, T const& e, Rank lo, Rank hi ) {while ( 1 < hi - lo ) { //每步迭代仅需做一次比较判断,有两个分支;成功查找不能提前终止Rank mi = ( lo + hi ) >> 1; //以中点为轴点(区间宽度折半,等效于其数值表示的右移一位)( e < S[mi] ) ? hi = mi : lo = mi; //经比较后确定深入[lo, mi)或[mi, hi)} //出口时hi = lo + 1,查找区间仅含一个元素A[lo]return e < S[lo] ? lo - 1 : lo; //返回位置,总是不超过e的最大者
} //有多个命中元素时,返回秩最大者;查找失败时,简单地返回-1,而不能指示失败的位置
有序向量:二分查找(C)
//二分查找算法(版本C):在有序向量的区间[lo, hi)内查找元素e,0 <= lo <= hi <= _size
template <typename T> static Rank binSearch( T* S, T const& e, Rank lo, Rank hi ) {while ( lo < hi ) { //每步迭代仅需做一次比较判断,有两个分支Rank mi = ( lo + hi ) >> 1; //以中点为轴点(区间宽度折半,等效于其数值表示的右移一位)( e < S[mi] ) ? hi = mi : lo = mi + 1; //经比较后确定深入[lo, mi)或(mi, hi)} //成功查找不能提前终止return lo - 1; //至此,[lo]为大于e的最小者,故[lo-1]即为不大于e的最大者
} //有多个命中元素时,返回最靠后者;查找失败时,返回失败的位置
与版本B的差异
1)待查找区间宽度缩短至e而非1时,算法才结束
2)转入右侧子向量时,左边界取作mi + 1而非mi——A[mi]会被遗漏?
3)无论成功与否,返回的秩严格符合接口的语义约定…
冒泡排序
向量元素若有序排列,计算效率将大大提升
template <typename T> void vector<T>::bubbleSort(Rank lo,Rank h1)
{ while (!bubble(lo,hi--)); } //逐趟做扫描交换,直至全序template <typename T> bool Vector<T>::bubble(Rank lo,Rank hi) {bool sorted = true; //整体有序标志while (++lo < hi) //自左向右,逐一检查各对相邻元素if (_elem[lo - 1] > _elem[lo]) { //若逆序,则sorted = false;//意味着尚未整体有序,并需要swap(_elem[lo - 1],_elem[lo]);//交换}return sorted; l/返回有序标志
}//乱序限于[0,√n)时,仍需O(n^{3/2})时间——按理,O(n)应已足矣
改进:
template <typename T> void vector<1>::bubbleSort(Rank lo,Rank h1)
{ while (lo < (hi = bubble(lo,hi)));}//逐趟扫描交换,直至全序
template <typename T> Rank Vector<T> : :bubble(Rank lo,Rank hi) {Rank last = lo;//最右侧的逆序对初始化为[lo - 1,1o]while (++lo < hi)//自左向右,逐一检查各对相邻元素if(_elem[lo - 1] > _elem[lo])//若逆序,则last = lo;//更新最右侧逆序对位置记录,并swap(_elem[lo - 1],_elem[lo]);//交换}return last;//返回最右侧的逆序对位置
}//前一版本中的逻辑型标志sorted,改为秩last
三种冒泡排序算法效率相同,最好o(n),最坏o(n^2)
在冒泡排序中,元素 a 和 b 的相对位置发生变化,只有一种可能;
1.经分别与其它元素的交换,二者相互接近直至相邻
2.在接下来一轮扫描交换中,二者因逆序而交换位置
归并排序
分治策略,向量与列表通用
序列一分为二 ( O ( 1 ) ) (\mathcal O(1)) (O(1)),子序列递归排序 ( 2 × T ( n / 2 ) ) (2 \times T(n/2)) (2×T(n/2)),合并有序子序列 ( O ( n ) ) (\mathcal O(n)) (O(n))
总体复杂度为 ( O ( n log n ) ) (\mathcal O(n\log n)) (O(nlogn))
template <typename T> //向量归并排序
void Vector<T>::mergeSort( Rank lo, Rank hi ) { // 0 <= lo < hi <= sizeif ( hi - lo < 2 ) return; //单元素区间自然有序,否则...Rank mi = ( lo + hi ) / 2; //以中点为界mergeSort( lo, mi ); mergeSort( mi, hi ); //前缀、后缀分别排序merge( lo, mi, hi ); //归并
}template <typename T> //对各自有序的[lo, mi)和[mi, hi)做归并
void Vector<T>::merge( Rank lo, Rank mi, Rank hi ) { // lo < mi < hiRank i = 0; T* A = _elem + lo; //合并后的有序向量A[0, hi - lo) = _elem[lo, hi)Rank j = 0, lb = mi - lo; T* B = new T[lb]; //前子向量B[0, lb) <-- _elem[lo, mi)for ( Rank i = 0; i < lb; i++ ) B[i] = A[i]; //复制出A的前缀Rank k = 0, lc = hi - mi; T* C = _elem + mi; //后缀C[0, lc) = _elem[mi, hi)就地while ( ( j < lb ) && ( k < lc ) ) //反复地比较B、C的首元素A[i++] = ( B[j] <= C[k] ) ? B[j++] : C[k++]; //将更小者归入A中while ( j < lb ) //若C先耗尽,则A[i++] = B[j++]; //将B残余的后缀归入A中——若B先耗尽呢?delete[] B; //释放临时空间:mergeSort()过程中,如何避免此类反复的new/delete?
}
算法的运行时间主要在于 for 循环,merge() 总体迭代不超过 O ( n ) \mathcal O(n) O(n) 次,累计只需线性时间。 T ( n ) = 2 T ( n / 2 ) + O ( n ) T(n) = 2T(n/2)+\mathcal O(n) T(n)=2T(n/2)+O(n)
位图
位图(Bitmap)是一种数据结构,用于表示一组位或二进制值的集合。在计算机科学中,位图通常用于存储和操作大量的二进制数据,其中每个位都表示某种状态或信息。
位图中的每个位(或者可以理解为数组的元素)代表一个元素是否存在于集合中。当元素存在时,对应位的值为1;不存在时,对应位的值为0。
相关文章:

数据结构和算法(2):向量
抽象数据类型 数组到向量 C/C 中,数组A[]中的元素与[0,n)内的编号一一对应,A[0],A[1],...,A[n-1];反之,每个元素均由(非负)编号唯一指代,并可直接访问A[i] 的物理地址 Ai s,s 为单…...

mysql 大表如何ddl
大家好,我是蓝胖子,mysql对大表(千万级数据)的ddl语句,在生产上执行时一定要千万小心,一不小心就有可能造成业务阻塞,数据库io和cpu飙高的情况。今天我们就来看看如何针对大表执行ddl语句。 通过这篇文章,…...
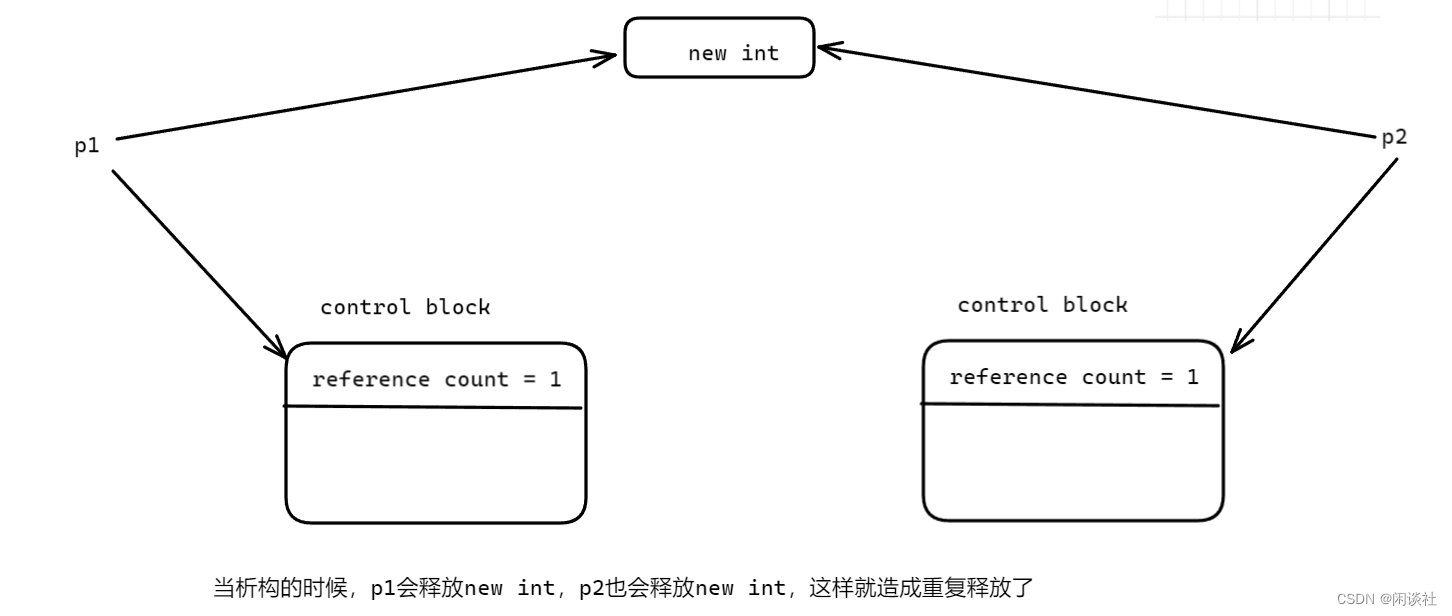
C++新特性:智能指针
一 、为什么需要智能指针 智能指针主要解决以下问题: 1)内存泄漏:内存手动释放,使用智能指针可以自动释放 2)共享所有权指针的传播和释放,比如多线程使用同一个对象时析构问题,例如同样的数据…...
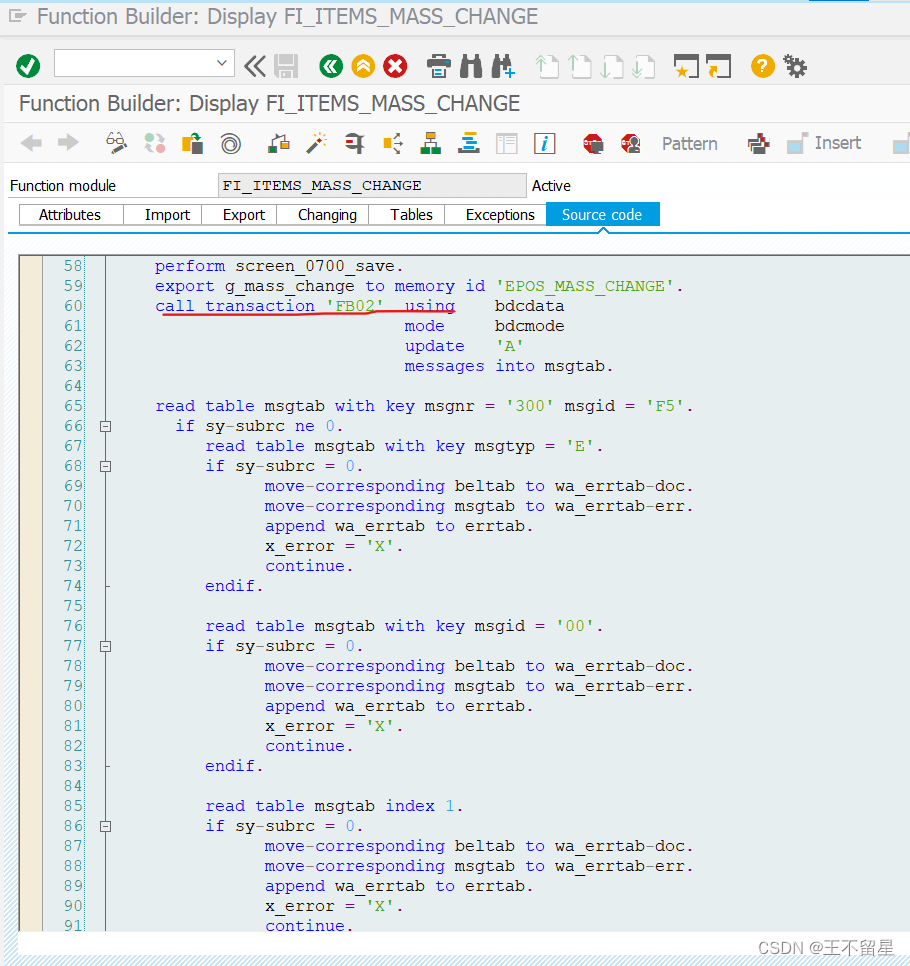
SAP FI之批量修改财务凭证的BAPI
文章目录 前言一、pandas是什么?二、使用步骤 1.引入库2.读入数据总结 前言 一般涉及修改财务凭证,或者其它凭证,不应直接更新数据库,而是使用系统提供的function module,或者BAPI,或者使用BDC。 一、 示例…...

Spring Boot + Vue的网上商城之商品分类
Spring Boot Vue的网上商城之商品分类 在网上商城中,商品分类是非常重要的一个功能,它可以帮助用户更方便地浏览和筛选商品。本文将介绍如何使用Spring Boot和Vue来实现商品分类的功能,包括一级分类和二级分类的管理以及前台按分类浏览商品…...

Docker 容器逃逸漏洞 (CVE-2020-15257)复现
漏洞概述 containerd是行业标准的容器运行时,可作为Linux和Windows的守护程序使用。在版本1.3.9和1.4.3之前的容器中,容器填充的API不正确地暴露给主机网络容器。填充程序的API套接字的访问控制验证了连接过程的有效UID为0,但没有以其他方式…...
Python 如何使用 csv、openpyxl 库进行读写 Excel 文件详细教程(更新中)
csv 基本概述 首先介绍下 csv (comma separated values),即逗号分隔值(也称字符分隔值,因为分隔符可以不是逗号),是一种常用的文本格式,用以存储表格数据,包括数字或者字符。 程序在处理数据时…...

$nextTick属性使用与介绍
属性介绍 $nextTick 是 Vue.js 中的一个重要方法,之前我们也说过$ref 等一些重要的属性,这次我们说$nextTick,$nextTick用于在 DOM 更新后执行回调函数。它通常用于处理 DOM 更新后的操作,因为 Vue 在更新 DOM 后不会立即触发回调…...

【群智能算法改进】一种改进的鹈鹕优化算法 IPOA算法[2]【Matlab代码#58】
文章目录 【获取资源请见文章第5节:资源获取】1. 原始POA算法2. 改进后的IPOA算法2.1 随机对立学习种群初始化2.2 动态权重系数2.3 透镜成像折射方向学习 3. 部分代码展示4. 仿真结果展示5. 资源获取 【获取资源请见文章第5节:资源获取】 1. 原始POA算法…...

k8s 入门到实战--部署应用到 k8s
k8s 入门到实战 01.png 本文提供视频版: 背景 最近这这段时间更新了一些 k8s 相关的博客和视频,也收到了一些反馈;大概分为这几类: 公司已经经历过服务化改造了,但还未接触过云原生。公司部分应用进行了云原生改造&…...

编程语言新特性:instanceof的改进
以前也写过类似的博文,可能重复。 要判断一个对象是哪个类或父类的实例,JAVA用到instanceof,其实语言也有类似语法。而类一般是多层继承的,有时就让人糊涂。所以我提出改进思路: instanceof:保持不变。ins…...
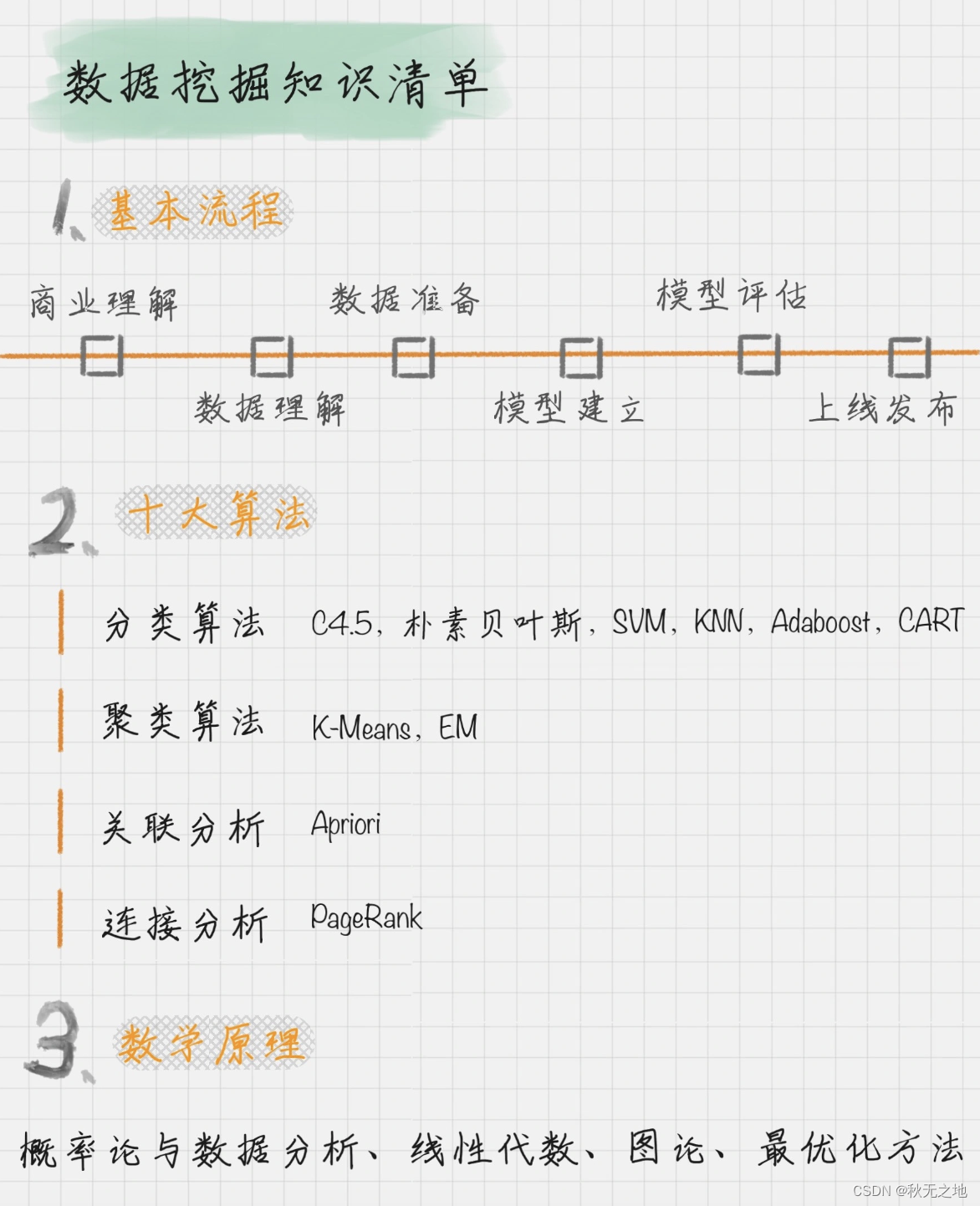
数据挖掘的学习路径
⭐️⭐️⭐️⭐️⭐️欢迎来到我的博客⭐️⭐️⭐️⭐️⭐️ 🐴作者:秋无之地 🐴简介:CSDN爬虫、后端、大数据领域创作者。目前从事python爬虫、后端和大数据等相关工作,主要擅长领域有:爬虫、后端、大数据…...
逻辑回归Logistic
回归 概念 假设现在有一些数据点,我们用一条直线对这些点进行拟合(这条直线称为最佳拟合直线),这个拟合的过程就叫做回归。进而可以得到对这些点的拟合直线方程。 最后结果用sigmoid函数输出 因此,为了实现 Logisti…...
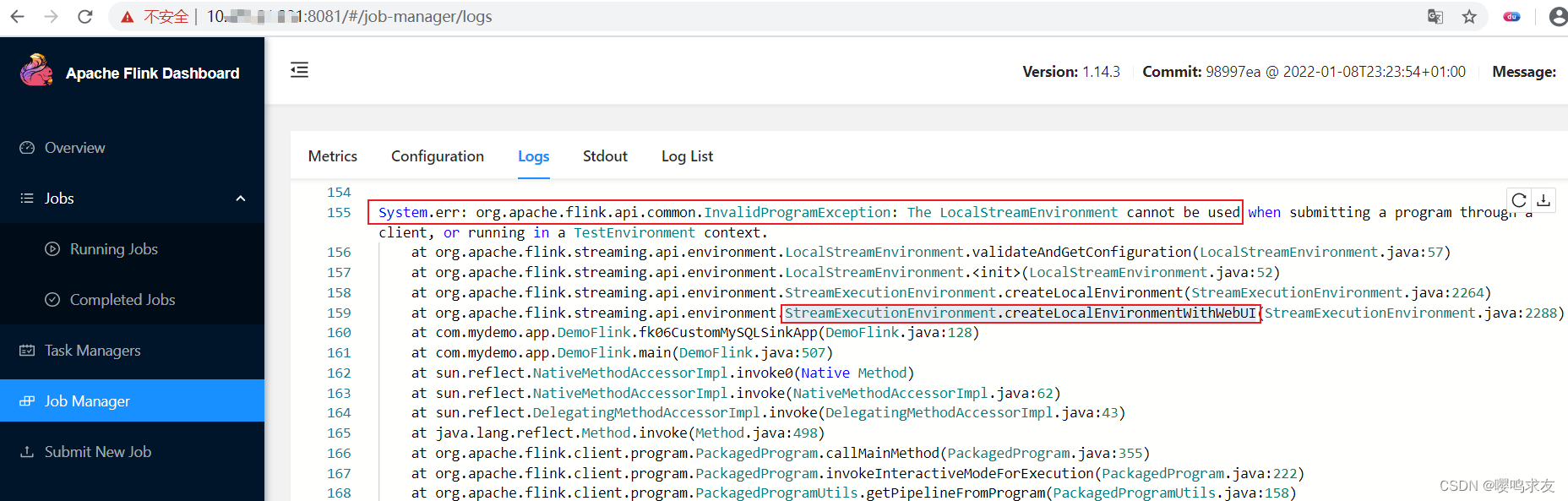
Flink提交jar出现错误RestHandlerException: No jobs included in application.
今天打包一个flink的maven工程为jar,通过flink webUI提交,发现居然报错。 如上图所示,提示错误为: Server Response Message: org.apache.flink.runtime.rest.handler.RestHandlerException: No jobs included in application. …...
】基础概念:数据仓库【用于决策的数据集合】的概念、建立数据仓库的原因与好处)
【数仓基础(一)】基础概念:数据仓库【用于决策的数据集合】的概念、建立数据仓库的原因与好处
文章目录 一. 数据仓库的概念1. 面向主题2. 集成3. 随时间变化4. 非易失粒度 二. 建立数据仓库的原因三. 使用数据仓库的好处 一. 数据仓库的概念 数据仓库的主要作用: 数据仓库概念主要是解决多重数据复制带来的高成本问题。 在没有数据仓库的时代,需…...
电商类面试问题--01Elasticsearch与Mysql数据同步问题
在实现基于关键字的搜索时,首先需要确保MySQL数据库和ES库中的数据是同步的。为了解决这个问题,可以考虑两层方案。 全量同步:全量同步是在服务初始化阶段将MySQL中的数据与ES库中的数据进行全量同步。可以在服务启动时,对ES库进…...
天线材质介绍--FPC天线
...

vue3 的 ref、 toRef 、 toRefs
1、ref: 对原始数据进行拷贝。当修改 ref 响应式数据的时候,模版中引用 ref 响应式数据的视图处会发生改变,但原始数据不会发生改变 <template><div>{{refA}}</div> </template><script lang"ts" setup> impor…...
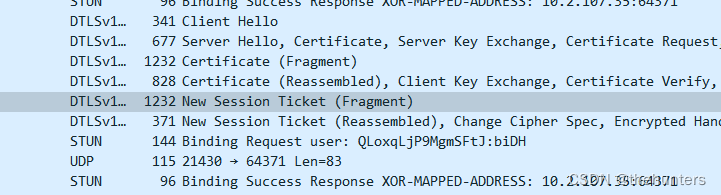
WebRTC中 setup:actpass、active、passive
1、先看一下整个DTLS的流程 setup:actpass、active、passive就发生在Offer sdp和Anser SDP中 Offer的SDP是setup:actpass,这个是服务方: v0\r o- 1478416022679383738 2 IN IP4 127.0.0.1\r s-\r t0 0\r agroup:BUNDLE 0 1\r aextmap-allow-mixed\r amsid-semanti…...

ModuleNotFoundError: No module named ‘lavis‘解决方案
大家好,我是爱编程的喵喵。双985硕士毕业,现担任全栈工程师一职,热衷于将数据思维应用到工作与生活中。从事机器学习以及相关的前后端开发工作。曾在阿里云、科大讯飞、CCF等比赛获得多次Top名次。现为CSDN博客专家、人工智能领域优质创作者。喜欢通过博客创作的方式对所学的…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...
