TiDB 一栈式综合交易查询解决方案获“金鼎奖”优秀金融科技解决方案奖
日前,2023“金鼎奖”评选结果揭晓, 平凯星辰(北京)科技有限公司研发的 TiDB 一栈式综合交易查询解决方案获“金鼎奖”优秀金融科技解决方案奖 , 该方案已成功运用于 多家国有大行、城商行和头部保险企业 。 此次获奖再次印证了平凯星辰在金融科技领域的创新实力。

“金鼎奖”由中国金融展组委会主办,评奖活动通过表彰金融类优秀科技、产品、解决方案及服务,通过大力宣传推广参展单位的新技术、新产品、新服务模式,不断推动金融与科技深度融合,提升我国金融行业的综合管理和服务水平,为激发行业创新动能和发展活力起到了重要的促进作用。
平凯星辰历经全球 3000 多家行业用户海量数据的严苛场景打磨,稳定可靠,具备金融关键核心业务的支撑能力。 其打造的 TiDB 一栈式综合交易查询解决方案在本次评选中脱颖而出,获“金鼎奖”优秀金融科技解决方案奖 。
TiDB 一栈式综合交易查询解决方案基于 TiDB 原生分布式架构和 HTAP 能力,利用 TiDB 的水平 扩展、高可用、行列混合、分布式事务等关键能力,为金融企业提供了同时满足高并发联机访问、大数据量批处理、高业务连续性保障的整体解决方案。
截止 2023 年 8 月,该方案已在 多家金融机构 成功投产且运行稳定, 为 金融机构实现技术自主、业务创新和降本增效目标提供了强大的支持。 在实际应用中具有以下优势:
○ 简化了金融企业的整体数据架构和数据链路,提升了数据质量和业务敏捷性;
○ 满足金融企业在实时交易汇聚、消费领域对于大容量、高访问量的非功能需求;
○ 在混合负载场景下,满足金融企业对于数据库多模存储引擎、统一访问入口、稳定性的需求;
○ 满足了金融企业对基础架构领域高可用、故障自动处理、同城双活、切换演练、大数据量备份方面的需求。
未来,平凯星辰将持续深耕金融科技领域,为金融行业提供更为先进、可靠的技术解决方案,推动行业数字化转型。
相关文章:

TiDB 一栈式综合交易查询解决方案获“金鼎奖”优秀金融科技解决方案奖
日前,2023“金鼎奖”评选结果揭晓, 平凯星辰(北京)科技有限公司研发的 TiDB 一栈式综合交易查询解决方案获“金鼎奖”优秀金融科技解决方案奖 , 该方案已成功运用于 多家国有大行、城商行和头部保险企业 。 此次获奖再…...
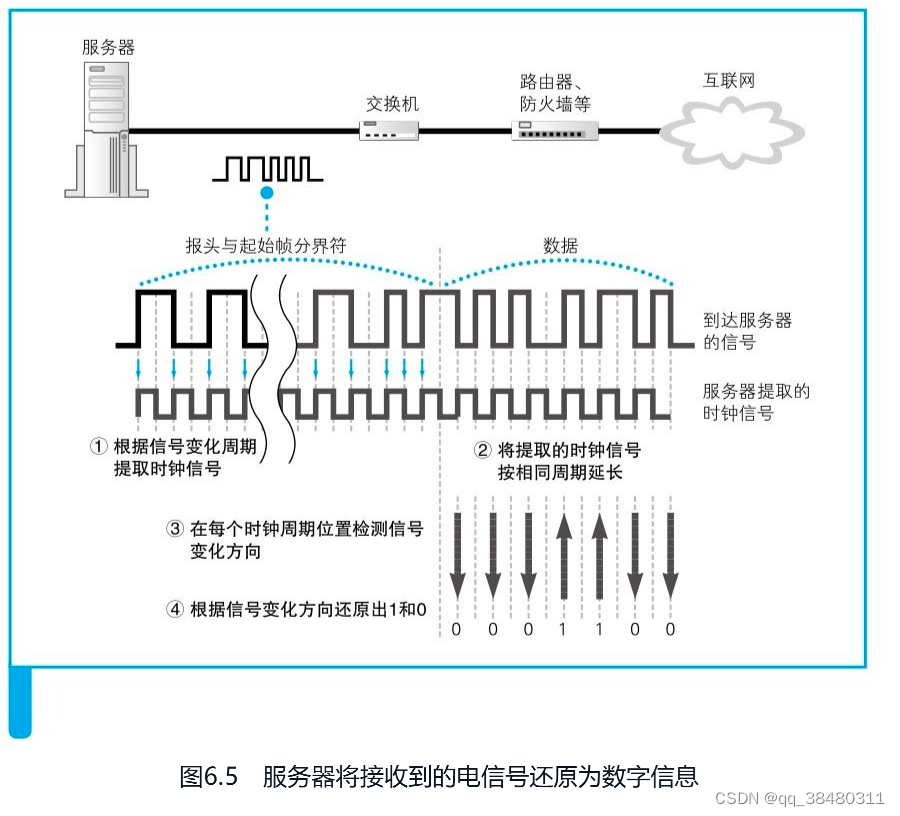
《网络是怎样连接的》(六)
本文主要取材于 《网络是怎样连接的》 第六章。 目录 6.1 服务器概览 6.2 服务器的接收操作 6.3 Web服务器程序解释请求消息并作出响应 6.4 浏览器接收响应消息并显示内容 简述:本文主要内容是解释 网络包到达服务器之后,如何给客户端响应的。 服务…...

2023年高教社杯数学建模国赛 赛题浅析
2023年国赛如期而至,为了方便大家尽快确定选题,这里将对赛题进行浅析,以分析赛题的主要难点、出题思路以及选择之后可能遇到的难点进行说明,方便大家尽快确定选题。 难度排序 B>A>C 选题人数 C>A>B (预估结果&…...
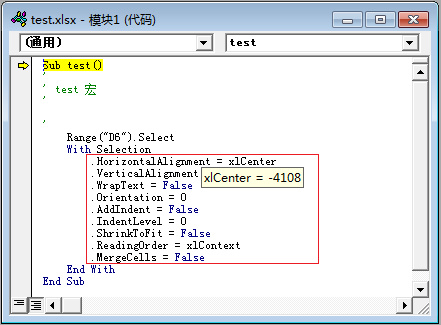
使用QT操作Excel 表格的常用方法
VBA 简介 Microsoft Office软件通常使用VBA来扩展Windows的应用程序功能,Visual Basic for Applications(VBA)是一种Visual Basic的一种宏语言。 在VBA的参考手册中就可以看到具体函数、属性的用法,Qt操作Excel主要通过 QAxObj…...
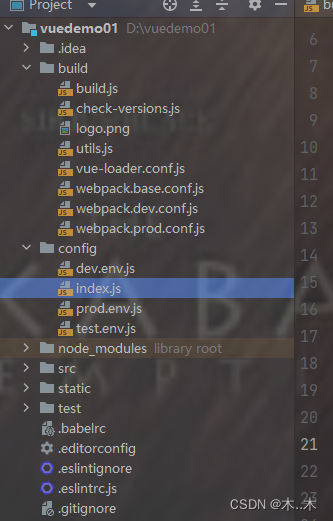
vue前后端端口不一致解决方案
在config index.js文件中 引入如下代码即可 const path require(path) const devEnv require(./dev.env) module.exports {dev: {// PathsassetsSubDirectory: static,assetsPublicPath: /,proxyTable: devEnv.OPEN_PROXY false ? {} : {/api: {target: http://localhos…...

springcloudSeata处理分布式事务之1.7.0
1.5.0之后版本发生了很大改变 1.seata安装 1.1官网地址 http://seata.io/zh-cn/ 1.2下载地址 https://github.com/seata/seata/releases 下载的是seata-server-1.7.0.zip 1.3seata相关配置的修改 seata-server-1.7.0\seata\conf下的application.yml进行修改 server:por…...

每日刷题|回溯法解决全排列问题
食用指南:本文为作者刷题中认为有必要记录的题目 前置知识:回溯法经典问题之组合 ♈️今日夜电波:爱人错过—告五人 1:11 ━━━━━━️💟──────── 4:52 …...

10-JVM调优工具详解
上一篇:09-JVM垃圾收集底层算法实现 前置启动程序 事先启动一个web应用程序,用jps查看其进程id,接着用各种jdk自带命令优化应用 1.Jmap 此命令可以用来查看内存信息,实例个数以及占用内存大小 jmap -histo 14660 #查看历史…...
)
东方博易oj——3119 - 约瑟夫问题2(链表)
文章目录 题目题目描述输入输出样例输入 输出标签 AC代码 题目 题目描述 约瑟夫问题:有 n n n只猴子,按顺时针方向围成一圈选大王(编号从 1 1 1到 n &#…...
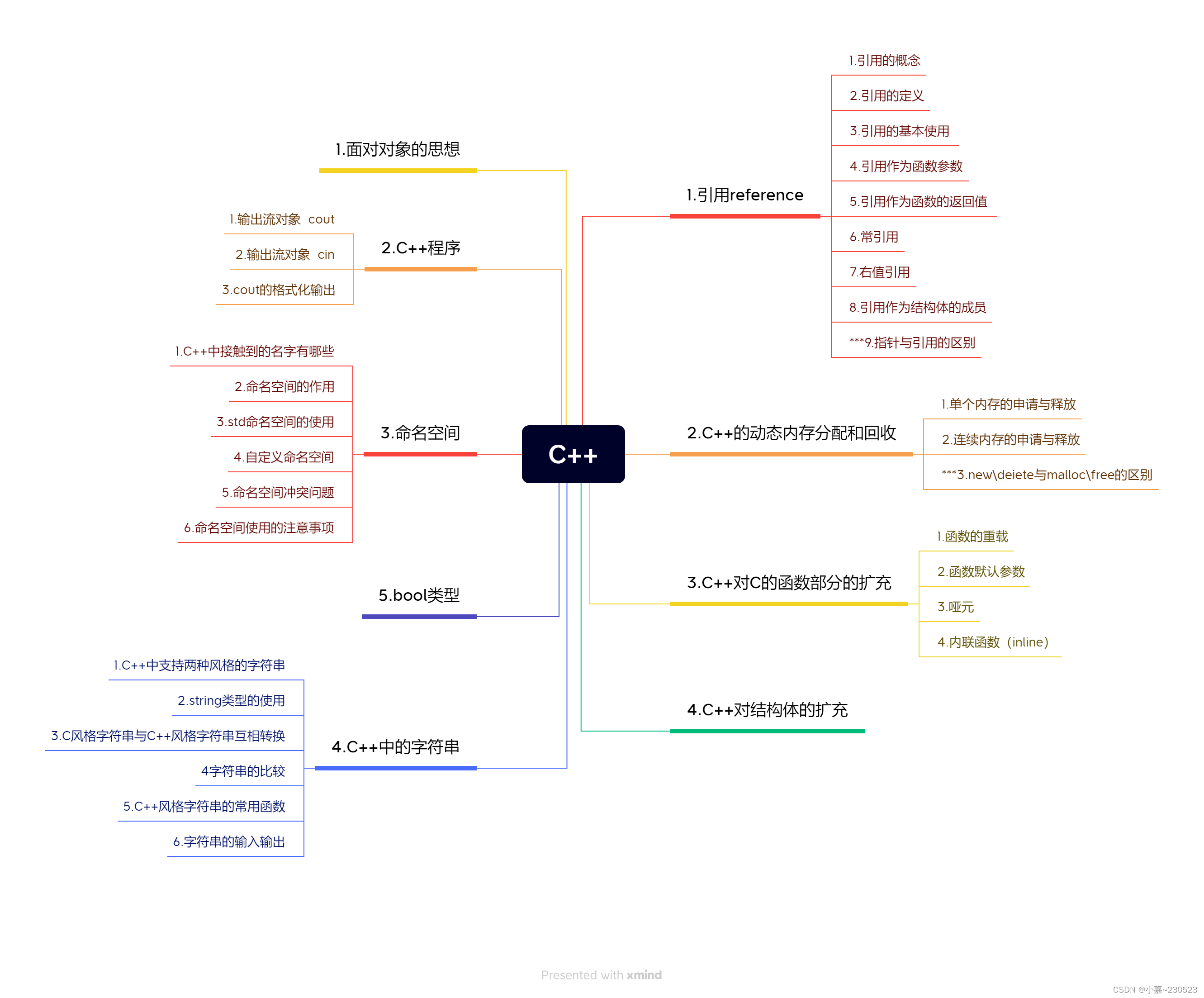
C++,day0907
#include <iostream>using namespace std; struct stu { private:int num; private:double score[32];public:void setNum(){cout <<"请输入学生人数:";cin >>num;}void input(){cout<<"请输入学生的成绩:"<<endl;for(int i…...

孤儿僵尸守护进程的简单理解
孤儿进程: 一个父进程退出,而它的一个或多个子进程还在运行,那么那些子进程将成为孤儿进程。孤儿进程将被init进程所收养,并由init进程对它们完成状态收集工作。 如何模仿一个孤儿进程: 答案是: kill 父…...

学习笔记——Java入门第一季
1.1 Java的介绍与前景 Java语言最早期的制作者:James Gosling(詹姆斯高斯林) 1995年5月23日,Sun Microsystems公司宣布Java语言诞生。 1.2 Java的特性与版本 跨平台 开源(开放源代码) Java代码ÿ…...
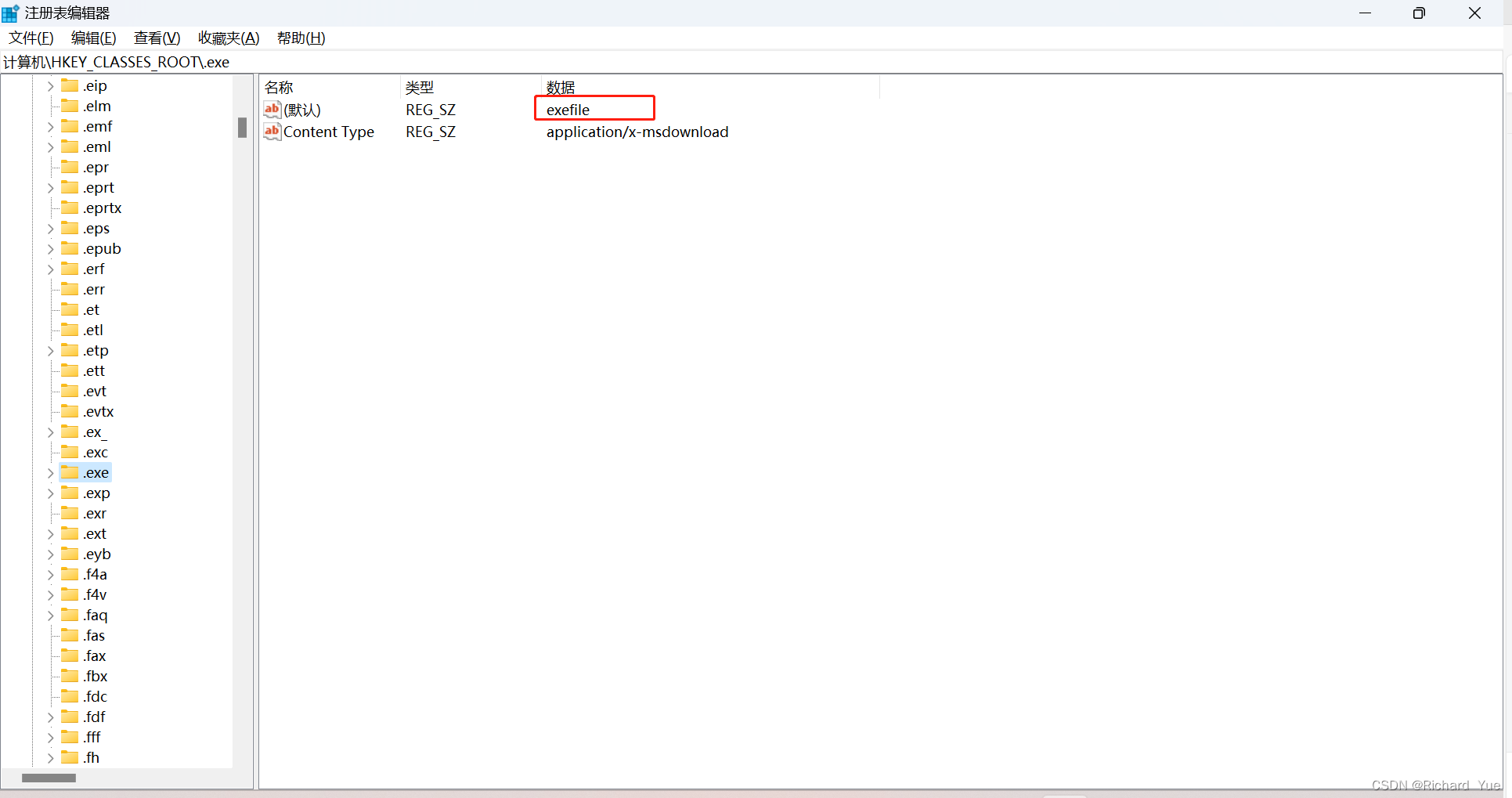
更改注册表exe值后的惨痛经历
装软件时由于执行性文件打不开,搜索教程更改了exefile的值,最后整个电脑崩了,所有EXE都打不开,折腾了5个小时,什么办法都试了,甚至重置电脑都不让,打算拿电脑城修电脑了,突然搜到了一…...

stable diffusion实践操作-LyCORIS
系列文章目录 stable diffusion实践操作 文章目录 系列文章目录前言一、LyCORIS是什么?二、使用步骤1.下载2.安装3 使用 二、整理模型1.LoHa-v1.0-pynoise 总结 前言 LyCORIS,可以理解为lora的加强版本。 LyCORIS - Lora beYond Conventional methods,…...
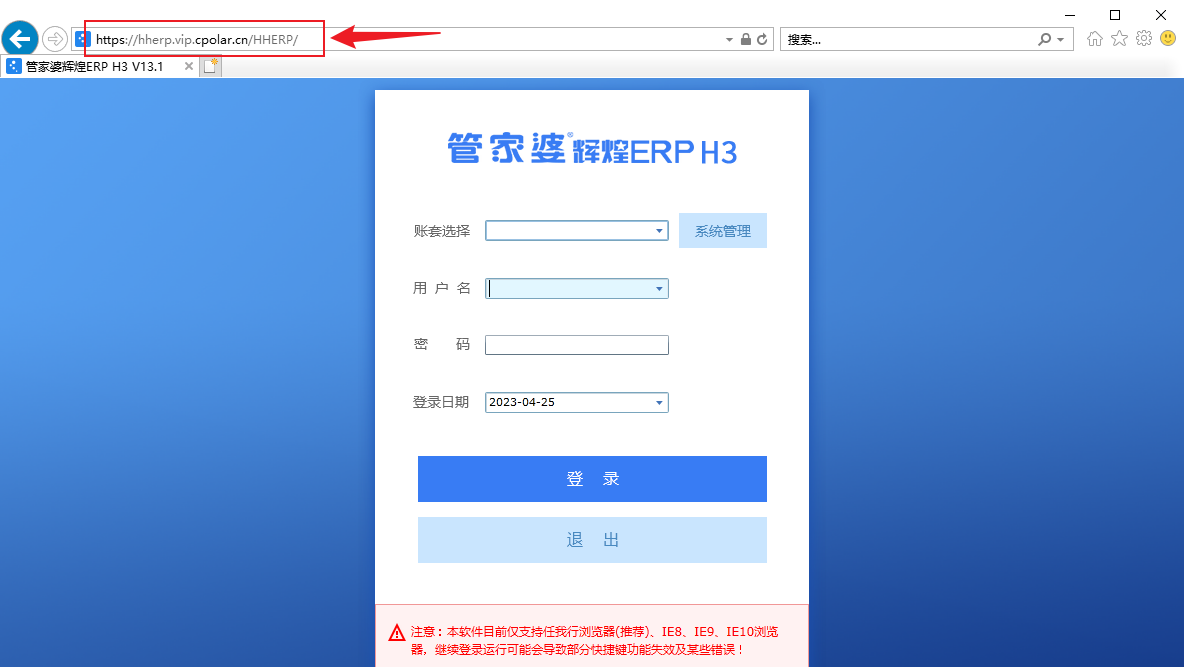
无需公网IP教你如何外网远程访问管家婆ERP进销存
文章目录 前言 1.管家婆服务2. 内网穿透2.1 安装cpolar内网穿透2.2 设置远程访问 3. 固定访问地址4. 配置固定公网访问地址 前言 管家婆辉煌系列产品是中小企业进销存、财务管理一体化的典范软件,历经十余年市场的洗礼,深受广大中小企业的欢迎ÿ…...

Swift使用编解码库Codable
Codable 是 Swift 引入的全新的编解码库,使开发者更方便的解析JSON 或 plist 文件。支持枚举、结构体和类。 Codable协议定义 Codable代表一个同时符合 Decodable 和 Encodable 协议的类型,即可解码且可编码的类型。 typealias Codable Decodable &a…...
Vue + Element UI 前端篇(三):工具模块封装
Vue Element UI 实现权限管理系统 前端篇(三):工具模块封装 封装 axios 模块 封装背景 使用axios发起一个请求是比较简单的事情,但是axios没有进行封装复用,项目越来越大,会引起越来越多的代码冗余&am…...
【pytorch】数据加载dataset和dataloader的使用
1、dataset加载数据集 dataset_tranform torchvision.transforms.Compose([torchvision.transforms.ToTensor(),])train_set torchvision.datasets.CIFAR10(root"./train_dataset",trainTrue,transformdataset_tranform,downloadTrue) test_set torchvision.data…...
搭建单机版FastDFS分布式文件存储系统
一、准备工作 1、下载FastDFS安装包和依赖包 https://codeload.github.com/happyfish100/libfastcommon/tar.gz/V1.0.43 https://codeload.github.com/happyfish100/fastdfs/tar.gz/V6.06 https://codeload.github.com/happyfish100/fastdfs-nginx-module/tar.gz/V1.22 注&…...
【验证码逆向专栏】房某下登录滑块逆向分析
声明 本文章中所有内容仅供学习交流使用,不用于其他任何目的,不提供完整代码,抓包内容、敏感网址、数据接口等均已做脱敏处理,严禁用于商业用途和非法用途,否则由此产生的一切后果均与作者无关! 本文章未…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...
