【DS思想+堆贪心】CF595div3 D2
Problem - D2 - Codeforces
题意:


思路:
大家都说这是典,但是我不懂怎么个典法,可能堆贪心都是这样做的吗,不懂
首先肯定要贪心,对于一个坏点,优先删除覆盖别的点多的
考虑nlogn做法,先去枚举点,然后把覆盖该点的所有区间扔进优先队列里,优先删除右端点靠右的
那怎么看是不是坏点,还得维护一个差分数组,边枚举边维护
感觉突破点就是堆贪心
Code:
#include <bits/stdc++.h>#define int long longusing i64 = long long;constexpr int N = 2e5 + 10;
constexpr int M = 1e6 + 10;
constexpr int P = 2600;
constexpr i64 Inf = 1e18;
constexpr int mod = 998244353;
constexpr double eps = 1e-6;struct ty {int l, r;int id;bool operator < (const ty & a) const {return a.r > r;}
}p[N];std::priority_queue<ty> q;int n, k;
int sum[N];
int ans[N];bool cmp(ty x, ty y) {if (x.l == y.l) return x.r < y.r;return x.l < y.l;
}
void solve() {std::cin >> n >> k;for (int i = 1; i <= n; i ++) {std::cin >> p[i].l >> p[i].r;p[i].id = i;sum[p[i].l] ++;sum[p[i].r + 1] --;}std::sort(p + 1, p + 1 + n, cmp);int j = 1;int len = 0;for (int i = 1; i < N; i ++) {while (j <= n && p[j].l <= i) q.push(p[j ++]);sum[i] += sum[i - 1];while (sum[i] > k) {auto u = q.top();q.pop();ans[++len] = u.id;sum[i] --;sum[u.r + 1] ++;}}std::cout << len << "\n";for (int i = 1; i <= len; i ++) std::cout << ans[i] << " \n" [i == len];
}
signed main() {std::ios::sync_with_stdio(false);std::cin.tie(nullptr);int t = 1;while (t--) {solve();}return 0;
}相关文章:

【DS思想+堆贪心】CF595div3 D2
Problem - D2 - Codeforces 题意: 思路: 大家都说这是典,但是我不懂怎么个典法,可能堆贪心都是这样做的吗,不懂 首先肯定要贪心,对于一个坏点,优先删除覆盖别的点多的 考虑nlogn做法&#x…...

2023-09-08 LeetCode每日一题(计算列车到站时间)
2023-09-08每日一题 一、题目编号 2651. 计算列车到站时间二、题目链接 点击跳转到题目位置 三、题目描述 给你一个正整数 arrivalTime 表示列车正点到站的时间(单位:小时),另给你一个正整数 delayedTime 表示列车延误的小时…...

软考-高级-信息系统项目管理第四版(完整24章全笔记)
《信息系统项目管理师教程》(第4版)是由全国计算机专业技术资格考试办公室组织编写的考试用书,根据2022年审定通过的《信息系统项目管理师考试大纲》编写,对信息系统项目管理师岗位所要求的主要知识及应用技术进行了阐述。 《信息…...

华为Mate 60和iPhone 15选哪个?
最近也有很多朋友问我这个问题来着,首先两款手机定位都是高端机,性能和体验各有千秋,各自有自己的铁杆粉。 但是让人意想不到的是华为mate60近日在海外越来越受欢迎和追捧,甚至是引起了不少人的抢购,外观设计和…...

嵌入式Linux驱动开发(同步与互斥专题)(二)
一、自旋锁spinlock的实现 自旋锁,顾名思义:自己在原地打转,等待资源可用,一旦可用就上锁霸占它。 ① 原地打转的是CPU x,以后CPU y会解锁:这涉及多个CPU,适用于SMP系统; ② 对于单…...
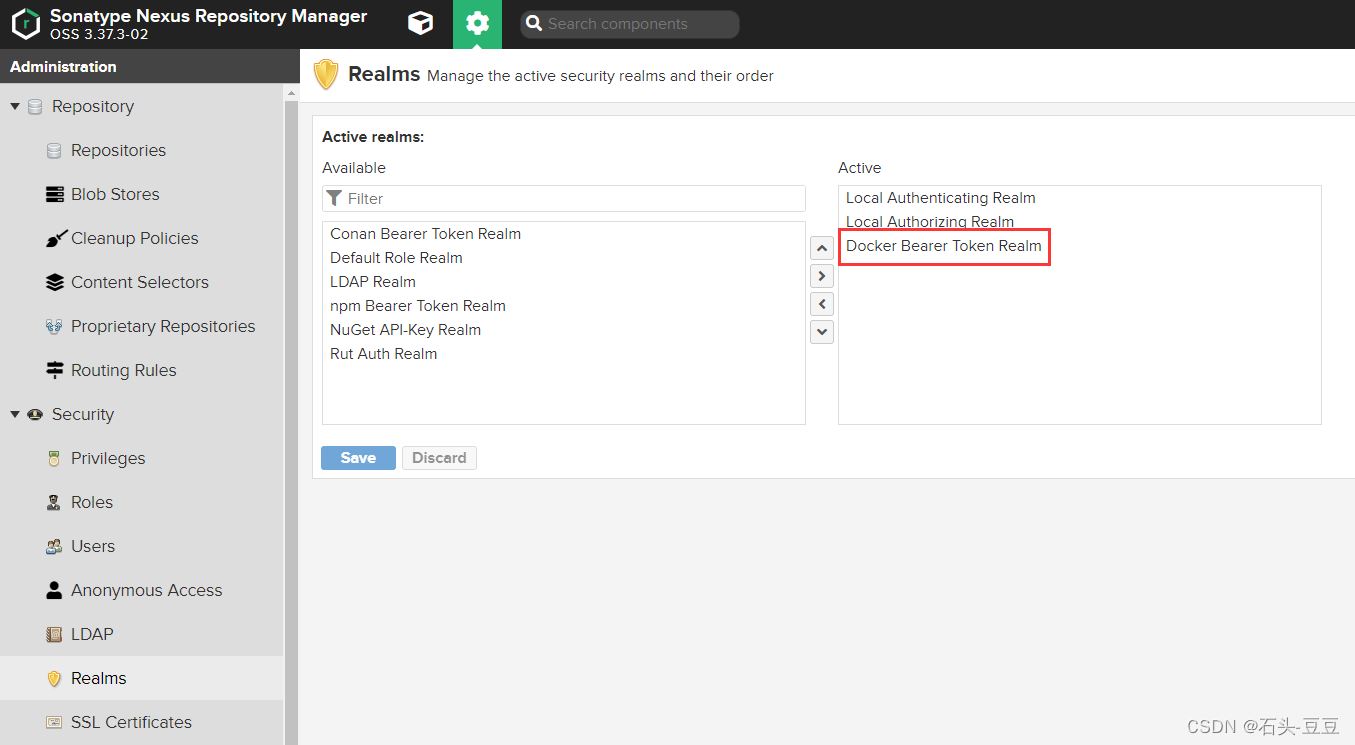
Docker安装部署Nexus3作为内网镜像代理缓存容器镜像
Docker安装部署Nexus3作为内网镜像代理 一、背景描述 基础镜像比较小,仓库使用阿里云或者腾讯云拉取速度挺快,但是时光飞逝几年时间过去,再加上AI加持的情况下,有些镜像的大小已经接近20G! 这种情况下不管是测试环境…...

SpringBoot工具库:解决SpringBoot2.*版本跨域问题
1.解决问题:When allowCredentials is true, xxxxxxx , using “allowedOriginPatterns“ instead 2.3版本跨域配置如下 /*** 跨域问题解决*/ Configuration public class CorsConfig implements WebMvcConfigurer {Overridepublic void addCorsMappings(CorsRegi…...
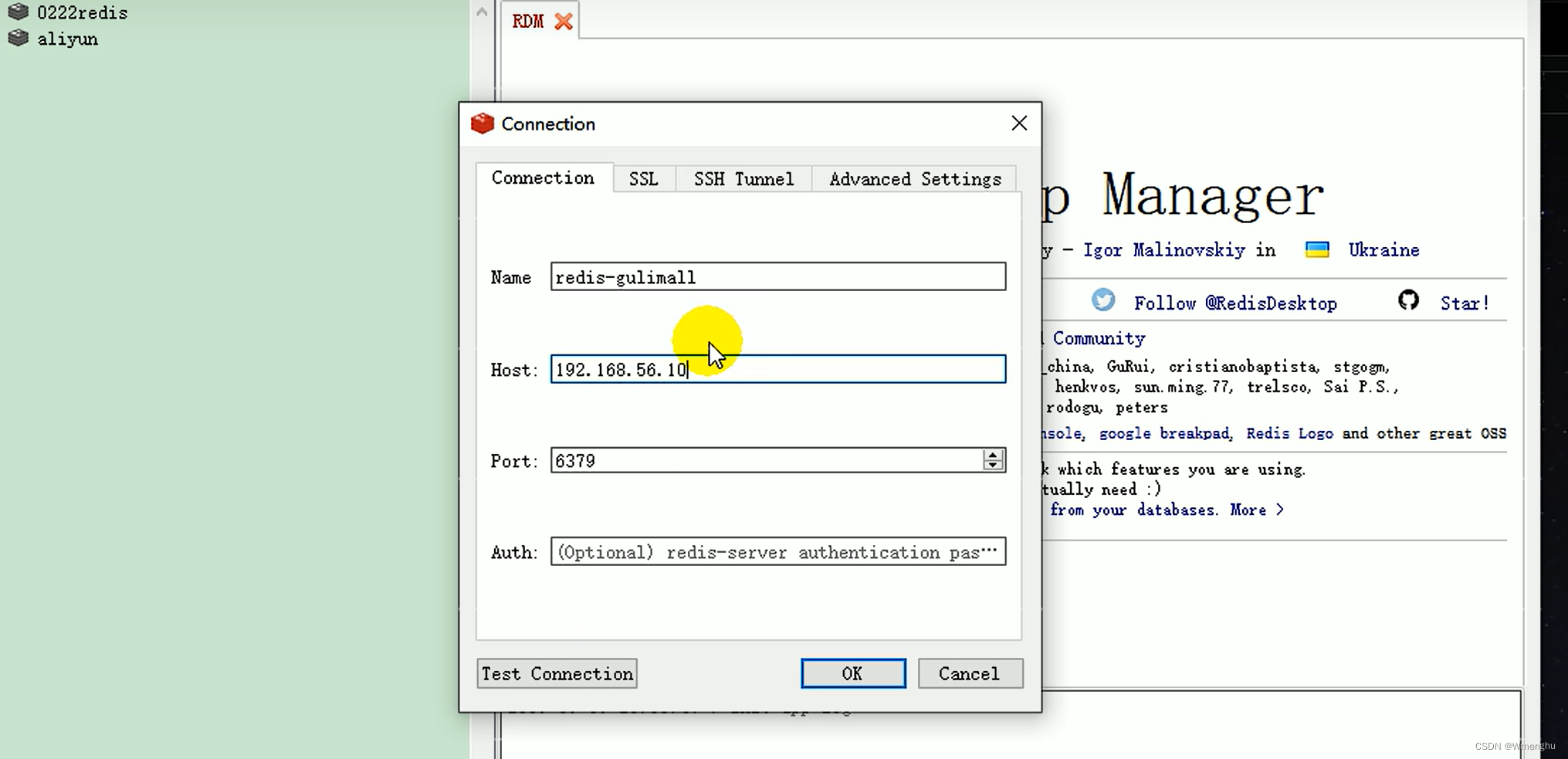
docker安装开发常用软件MySQL,Redis,rabbitMQ
Docker安装 docker官网:Docker: Accelerated Container Application Development docker镜像仓库:https://hub.docker.com/search?qnginx 官网的安装教程:Install Docker Engine on CentOS | Docker Docs 安装步骤 1、卸载以前安装的doc…...

C# Unity FSM 状态机
C# Unity FSM 状态机 使用状态机可以降低代码耦合性,并且可以优化代码可读性,方便团队协作等。 对于游戏开发内容来讲游戏开发的流程控制玩家动画都可以使用FSM有限状态机来实现。 1.FsmState 每个状态的基类,泛型参数表示所拥有者 publi…...

pytorch搭建squeezenet网络的整套工程,及其转tensorrt进行cuda加速
本来,前辈们用caffe搭建了一个squeezenet的工程,用起来也还行,但考虑到caffe的停更后续转trt应用在工程上时可能会有版本的问题所以搭建了一个pytorch版本的。 以下的环境搭建不再细说,主要就是pyorch,其余的需要什么p…...

【精读Uboot】SPL阶段的board_init_r详细分析
对于i.MX平台上的SPL来说,其不会直接跳转到Uboot,而是在SPL阶段借助BOOTROM跳转到ATF,然后再通过ATF跳转到Uboot。 board_init_f会初始化设备相关的硬件,最后进入board_init_r为镜像跳转做准备。下面是board_init_r调用的核心函数…...
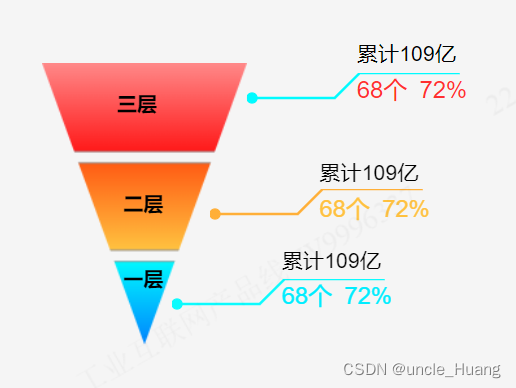
canvas绘制渐变色三角形金字塔
项目需求:需要绘制渐变色三角形金字塔,并用折线添加标识 (其实所有直接用图片放上去也行,但是ui没切图,我也懒得找她要,正好也没啥事,直接自己用代码绘制算了,总结一句就是闲的) 最终效果如下图: (以上没用任何图片,都是代码绘制的) 在网上找了,有用canvas绘…...
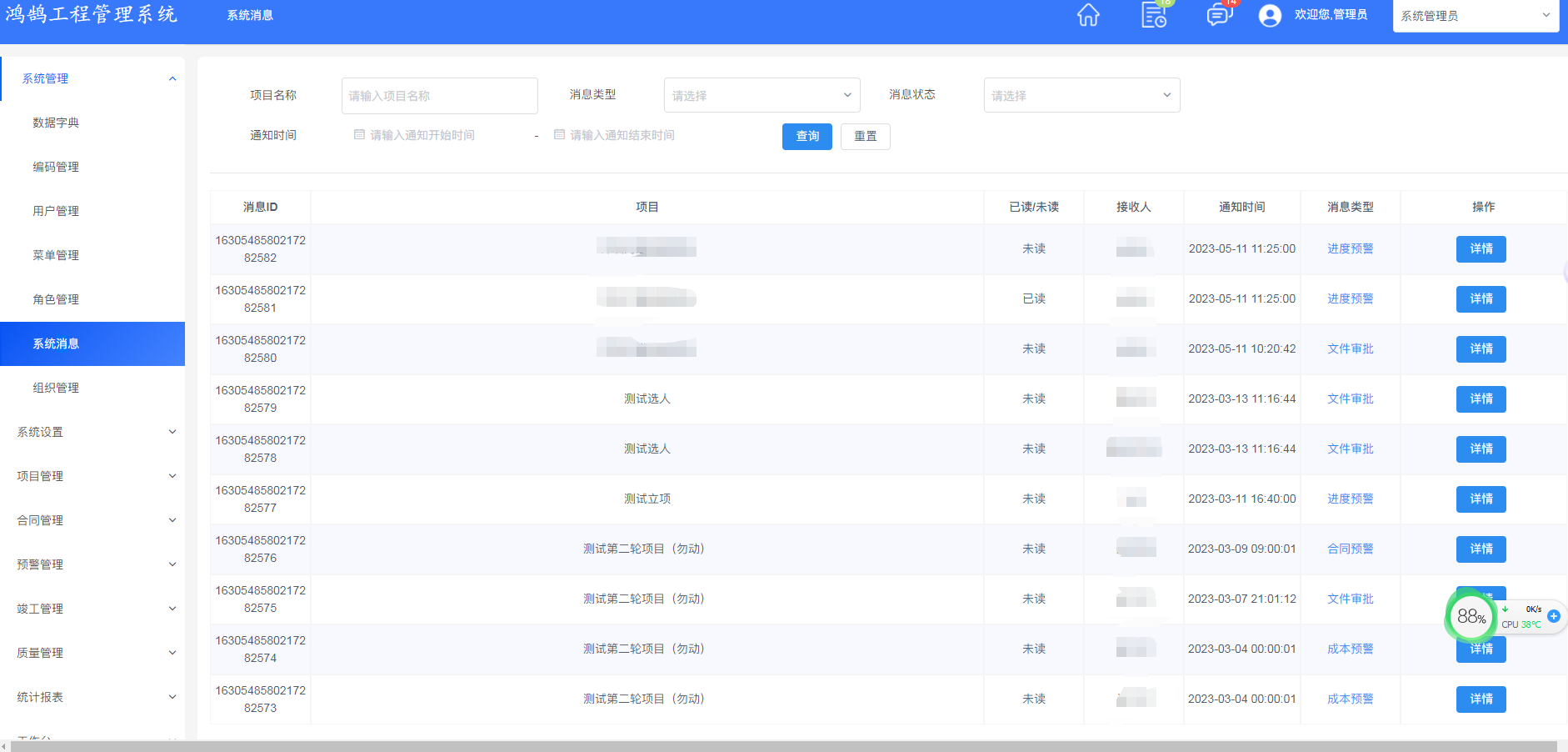
企业电子招标采购系统源码Spring Boot + Mybatis + Redis + Layui + 前后端分离 构建企业电子招采平台之立项流程图
功能模块: 待办消息,招标公告,中标公告,信息发布 描述: 全过程数字化采购管理,打造从供应商管理到采购招投标、采购合同、采购执行的全过程数字化管理。通供应商门户具备内外协同的能力,为外部供…...

Debain JDK8 安装
Debain JDK8 安装 首先请安装依赖: sudo apt-get update && sudo apt-get install -y wget apt-transport-https然后信任 GPG 公钥: wget -O - https://packages.adoptium.net/artifactory/api/gpg/key/public | sudo tee /etc/apt/keyrings/…...

Python序列操作指南:列表、字符串和元组的基本用法和操作
文章目录 序列列表创建列表访问元素修改元素添加和删除元素 range()字符串创建字符串访问字符字符串切片修改字符串 元组创建元组访问元素获取元素数量元组的特点: 可变对象改变对象的值改变变量的指向比较运算符总结 python精品专栏推荐python基础知识(…...
【已更新代码图表】2023数学建模国赛E题python代码--黄河水沙监测数据分析
E 题 黄河水沙监测数据分析 黄河是中华民族的母亲河。研究黄河水沙通量的变化规律对沿黄流域的环境治理、气候变 化和人民生活的影响,以及对优化黄河流域水资源分配、协调人地关系、调水调沙、防洪减灾 等方面都具有重要的理论指导意义。 附件 1 给出了位于小浪底水…...
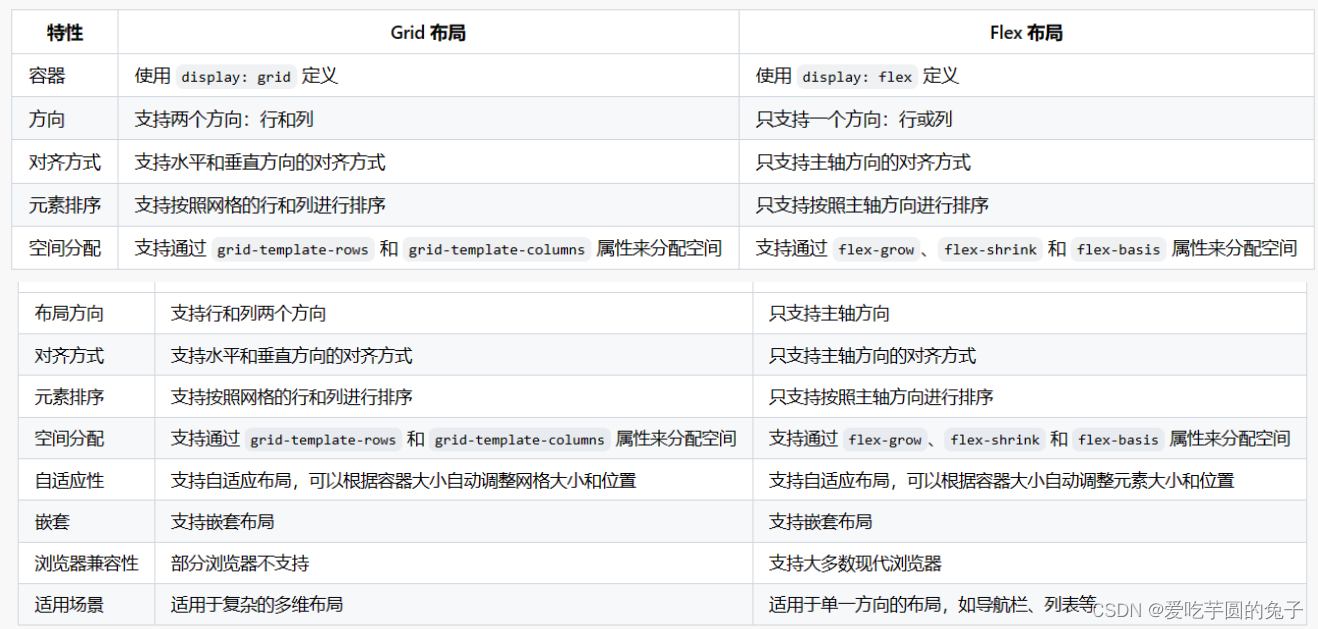
【前端】CSS-Grid网格布局
目录 一、grid布局是什么二、grid布局的属性三、容器属性1、display①、语句②、属性值 2、grid-template-columns属性、grid-template-rows属性①、定义②、属性值1)、固定的列宽和行高2)、repeat()函数3)、auto-fill关键字4)、f…...

计算机竞赛 基于深度学习的动物识别 - 卷积神经网络 机器视觉 图像识别
文章目录 0 前言1 背景2 算法原理2.1 动物识别方法概况2.2 常用的网络模型2.2.1 B-CNN2.2.2 SSD 3 SSD动物目标检测流程4 实现效果5 部分相关代码5.1 数据预处理5.2 构建卷积神经网络5.3 tensorflow计算图可视化5.4 网络模型训练5.5 对猫狗图像进行2分类 6 最后 0 前言 &#…...

2023-9-8 求组合数(二)
题目链接:求组合数 II #include <iostream> #include <algorithm>using namespace std;typedef long long LL; const int mod 1e9 7; const int N 100010;// 阶乘,阶乘的逆 int fact[N], infact[N];LL qmi(int a, int k, int p) {int res…...

k8s service的一些特性
文章目录 Service分发负载的策略同一端口通过不同协议暴露Headless Service的负载分发策略 Service分发负载的策略 大家都知道,一个service可以对应多个pod,那么一定要有一些方法来把service接收到的请求(负载)转发到pod上。 一般…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...
