Java 语言实现最小生成树算法(如Prim算法、Kruskal算法)
引言:
在图论中,最小生成树是指一个无向图的生成树,其所有边的权值之和最小。解决最小生成树问题的两种主要算法是Prim算法和Kruskal算法。本文将深入探讨这两种算法并比较它们的优缺点,以帮助读者更好地理解最小生成树算法的原理和实现。
一、Prim算法
-
算法原理
Prim算法是一种贪心算法,通过逐步扩展生成树的边来构造最小生成树。算法开始时选择一个起始顶点,然后将该顶点添加到生成树中。之后,每次将离生成树最近的顶点添加到生成树中,并将所选顶点与其余顶点的边进行比较,选择最小边加入生成树,直至所有顶点都加入生成树。 -
算法步骤
- 创建一个空的生成树和一个空的顶点集合;
- 选择一个起始顶点,将其加入生成树,并将其标记为已访问;
- 重复以下步骤,直到所有顶点都加入生成树:
a) 从已访问的顶点中,选择一条边的权值最小的未访问顶点;
b) 将该未访问顶点加入生成树,并将其标记为已访问;
c) 更新生成树和未访问顶点的权值。
-
算法实现
实现Prim算法的关键是选择起始顶点和找到离生成树最近的未访问顶点。可以使用优先队列等数据结构来快速找到最小边。
二、Kruskal算法
-
算法原理
Kruskal算法是一种基于边的贪心算法,通过逐渐选择权值最小的边来构造最小生成树。算法将图中所有边按照权值从小到大排序,然后从最小权值的边开始逐一添加到生成树中,直到生成树包含了所有顶点。 -
算法步骤
- 创建一个空的生成树和一个空的边集合;
- 将图中所有边按照权值从小到大排序;
- 逐一选择未加入生成树的边,如果该边的两个顶点不在同一个连通分量中,则将该边加入生成树,并将两个顶点合并为一个连通分量;
- 重复步骤3,直到生成树包含了所有顶点。
-
算法实现
实现Kruskal算法的关键是边的排序和判断两个顶点是否在同一个连通分量中。可以使用并查集等数据结构来快速判断连通分量,并在添加边时更新并查集。
三、Prim算法 vs Kruskal算法
-
时间复杂度
Prim算法的时间复杂度为O(|V|^2),其中|V|表示顶点数。Kruskal算法的时间复杂度为O(|E|log|E|),其中|E|表示边数。从时间复杂度上来看,当图稠密时,Prim算法的效率更高,而当图稀疏时,Kruskal算法效率更高。 -
空间复杂度
Prim算法和Kruskal算法的空间复杂度均为O(|V|+|E|),其中|V|表示顶点数,|E|表示边数。 -
适用性
Prim算法适用于带权值的稠密图,而Kruskal算法适用于带权值的稀疏图。此外,如果需要在不连通的图中找出最小生成树,Kruskal算法是更好的选择。
结论:
最小生成树算法是图算法中重要且实用的算法之一。本文深入探讨了Prim算法和Kruskal算法的原理和实现,并比较了它们的优缺点。根据具体问题的特点和数据的特征,可以选择适合自己的算法来解决最小生成树问题。
import java.util.*;class Edge {int src, dest, weight;Edge(int src, int dest, int weight) {this.src = src;this.dest = dest;this.weight = weight;}
}class Graph {int V, E;List<Edge> edges;Graph(int vertices, int edges) {this.V = vertices;this.E = edges;this.edges = new ArrayList<>();}void addEdge(int src, int dest, int weight) {Edge edge = new Edge(src, dest, weight);edges.add(edge);}// Prim's algorithm for Minimum Spanning Treevoid primMST() {int[] parent = new int[V];int[] key = new int[V];boolean[] mstSet = new boolean[V];// Initialize key and mstSet arraysfor (int i = 0; i < V; i++) {key[i] = Integer.MAX_VALUE;mstSet[i] = false;}key[0] = 0;parent[0] = -1;for (int count = 0; count < V - 1; count++) {int u = getMinimumKey(key, mstSet);mstSet[u] = true;for (Edge edge : edges) {if (edge.src == u && !mstSet[edge.dest] && edge.weight < key[edge.dest]) {parent[edge.dest] = u;key[edge.dest] = edge.weight;}}}printMST(parent, key);}int getMinimumKey(int[] key, boolean[] mstSet) {int min = Integer.MAX_VALUE;int minIndex = -1;for (int v = 0; v < V; v++) {if (!mstSet[v] && key[v] < min) {min = key[v];minIndex = v;}}return minIndex;}void printMST(int[] parent, int[] key) {System.out.println("Prim's Minimum Spanning Tree:");System.out.println("Edge \tWeight");for (int i = 1; i < V; i++) {System.out.println(parent[i] + " - " + i + "\t" + key[i]);}}// Kruskal's algorithm for Minimum Spanning Treevoid kruskalMST() {List<Edge> result = new ArrayList<>();Collections.sort(edges, Comparator.comparingInt(edge -> edge.weight));UnionFind uf = new UnionFind(V);for (Edge edge : edges) {int srcRoot = uf.find(edge.src);int destRoot = uf.find(edge.dest);if (srcRoot != destRoot) {result.add(edge);uf.union(srcRoot, destRoot);}}printMST(result);}void printMST(List<Edge> result) {System.out.println("Kruskal's Minimum Spanning Tree:");System.out.println("Edge \tWeight");for (Edge edge : result) {System.out.println(edge.src + " - " + edge.dest + "\t" + edge.weight);}}
}class UnionFind {int[] parent;int[] rank;UnionFind(int n) {parent = new int[n];rank = new int[n];for (int i = 0; i < n; i++) {parent[i] = i;}}int find(int x) {if (parent[x] != x) {parent[x] = find(parent[x]);}return parent[x];}void union(int x, int y) {int xRoot = find(x);int yRoot = find(y);if (rank[xRoot] < rank[yRoot]) {parent[xRoot] = yRoot;} else if (rank[xRoot] > rank[yRoot]) {parent[yRoot] = xRoot;} else {parent[yRoot] = xRoot;rank[xRoot]++;}}
}public class Main {public static void main(String[] args) {int V = 4;int E = 5;Graph graph = new Graph(V, E);graph.addEdge(0, 1, 10);graph.addEdge(0, 2, 6);graph.addEdge(0, 3, 5);graph.addEdge(1, 3, 15);graph.addEdge(2, 3, 4);graph.primMST();System.out.println();graph.kruskalMST();}
}
这是一个使用Java语言实现的最小生成树算法的示例代码。代码中包含了Prim算法和Kruskal算法的实现,并提供了一个简单的图示例进行测试。通过调用primMST()和kruskalMST()方法,可以分别使用Prim算法和Kruskal算法计算出图的最小生成树,并将结果打印到控制台上。
在示例代码中,Graph类表示一个图,primMST()方法实现了Prim算法,kruskalMST()方法实现了Kruskal算法。辅助类Edge表示图中的边,UnionFind类实现了并查集用于Kruskal算法中的连通性判断。
通过运行示例代码,可以看到Prim算法和Kruskal算法分别计算出的最小生成树结果,并输出到控制台上。可以根据自己的需求和图的特点,使用不同的算法来解决最小生成树问题。
相关文章:
)
Java 语言实现最小生成树算法(如Prim算法、Kruskal算法)
引言: 在图论中,最小生成树是指一个无向图的生成树,其所有边的权值之和最小。解决最小生成树问题的两种主要算法是Prim算法和Kruskal算法。本文将深入探讨这两种算法并比较它们的优缺点,以帮助读者更好地理解最小生成树算法的原理…...

什么是Linux的Overcommit和OOM
overcommit_memory参数说明: 设置内存分配策略(可选,根据服务器的实际情况进行设置) /proc/sys/vm/overcommit_memory 可选值:0、1、2。 0, 表示内核将检查是否有足够的可用内存供应用进程使用…...
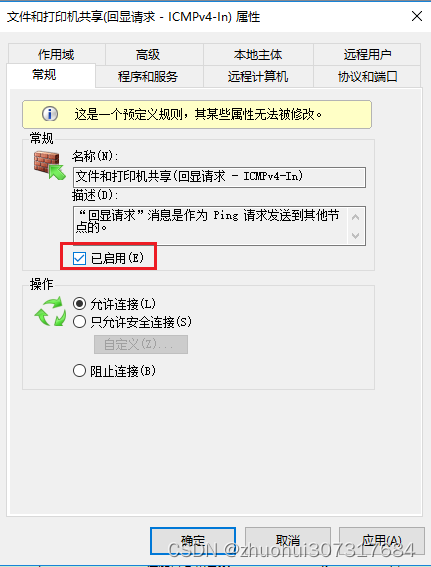
解决防火墙导致虚拟机不能ping通宿主机的问题
今天,无缘无故的,虚拟机突然用不了,网络连上不了,一番折腾翻找,最后才发现,是因为虚拟机ping不同宿主主机了,连网关都ping不通了,但是,宿主主机却可以ping通虚拟机 。 最…...
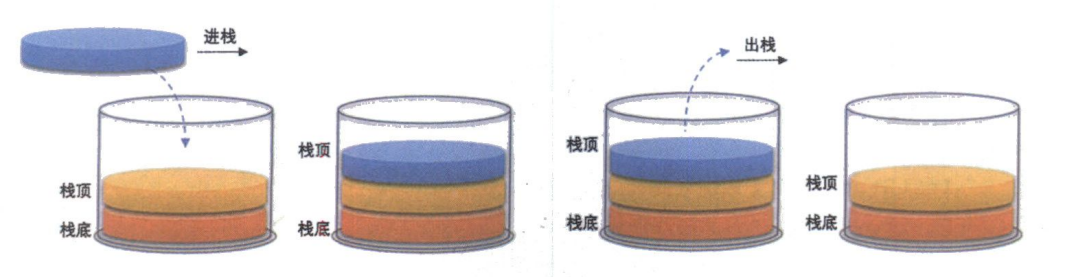
数据结构:线性表(栈的实现)
文章目录 1. 栈(Stack)1.1 栈的概念1.2 栈的结构链表栈数组栈 2. 栈的定义3. 栈的实现3.1 初始化栈 (StackInit)3.2 入栈 (StackPush)3.3 出栈 (StackPop)3.4 检测栈是否为空 (StackEmpty)3.5 获取栈顶元素 (StackTop)3.6 获取栈中有效元素个数 (StackSize)3.7 销毁栈 (StackDe…...

python如何将一个dataframe快速写入clickhouse
目录 前言思路与核心代码优缺点分析 前言 dataframe是用python做数据分析最场景的数据结构了,如何将dataframe数据快速写入到clickhouse数据库呢?这里介绍几种方法,各有优劣势,可以结合自己的使用场景挑用。 思路与核心代码 假…...
Tiny Player Mac:小而美,音乐播放的极致体验
对于追求音质和操作简便的Mac用户来说,Tiny Player Mac是一款不可多得的音乐播放器。它以简洁的界面、强大的功能和优异的性能,吸引了无数用户的目光。接下来,让我们一起了解这款小而美的音乐播放器。 Tiny Player Mac支持多种音频格式&#…...

2022年12月 C/C++(五级)真题解析#中国电子学会#全国青少年软件编程等级考试
C/C++编程(1~8级)全部真题・点这里 第1题:漫漫回国路 2020年5月,国际航班机票难求。一位在美国华盛顿的中国留学生,因为一些原因必须在本周内回到北京。现在已知各个机场之间的航班情况,求问他回不回得来(不考虑转机次数和机票价格)。 时间限制:1000 内存限制:65536 …...

C语言学习:7、break与continue的用法
前面讲到的循环体,貌似能解决生活中的很多问题,毕竟生活中很多事情是在重复的。但有时候也会有些小插曲,比如你在日复一日的上班,但某一天又特殊的事情你失业了,不就没班上了吗,那就得跳出那个上班的循环了…...

Ubuntu中安装clion并把clion添加到桌面快捷方式
Clion的安装: CLion是由大名鼎鼎的JetBrains公司出品的一款面向C和C的集成开发工具。下载地址。 下载后解压出来,然后进入到解压后的文件夹里面,执行 ./clion.sh 便可以运行软件: cd bin/ ./clion.sh 激活使用的话&…...

如何利用python来提取SQL语句中的表名称
1.介绍 在某些场景下,我们可能需要从一个复杂的SQL语句中提取对应的表名称,在这样的场景下,我们如果在python中处理的话,就需要用到SQLparse这个库。 SQLparse 是一个用于解析 SQL 查询语句的 Python 库。它可以将复杂的 SQL 查询…...
)
linux通用时钟框架(CCF)
目录 前言CCF 介绍提供者和消费者的概念CCF 框架组成关系CCF 程序关键结构体 CCF 重要组成注册时钟未使用设备树的时钟注册操作使用设备树的时钟注册操作 从使用的角度看CCF 前言 linux 内核版本 v4.19 嵌入式平台rv1109 , 文中代码出处。 CCF 介绍 提供者和消费者的概念 C…...
基于AERMOD模型在大气环境影响评价中的实践技术应用
随着我国经济快速发展,我国面临着日益严重的大气污染问题。近年来,严重的大气污染问题已经明显影响国计民生,引起政府、学界和人们越来越多的关注。大气污染是工农业生产、生活、交通、城市化等方面人为活动的综合结果,同时气象因…...

企业内训课程、在线教育平台付费课程加密防下载的10种方式
企业内训课程、在线教育平台付费课程加密防下载的10种方式: 实例演示:课程视频-第1课状语从句,VRM演示应用 企业内训课程、在线教育平台付费课程,他们的这种视频课程的加密是如何做的?整理了10种思路,供大家参考&…...

公关世界杂志公关世界杂志社公关世界编辑部2023年第14期目录
封面印象 画里有大美 笔下有乾坤——品读吴建潮的绘画艺术和诗文创作 赵铁信; 4-9 专题报道 “安济欣看千年济,李春赢得万口春”——赵州桥诗词楹联文化鉴赏暨沈鹏书法艺术研讨会举行 刘占行; 10-14 中国书协第二三届理事、河北省书协原副主席兼秘书长、…...
命令大全)
Linux常用(实用)命令大全
pwd 显示当前工作路径 shutdown 关闭系统 /halt 关闭系统 shutdown -r now 重启 /reboot 重启 systemctl stop firewalld 关闭防火墙 ip addr 查看ip地址. 1、cd命令:用于切换当前目录(可以是绝对路径,也可以是相对路径)如&#x…...

2023-09-07力扣每日一题
链接: [2594. 修车的最少时间](https://leetcode.cn/problems/form-smallest-number-from-two-digit-arrays/) 题意: 一个能力R的人R*N*N分钟修N辆车,求最快多久修完(多人多车) 解: 二分很好想&#x…...
next_permutation刷力扣)
从C语言到C++_39(C++笔试面试题)next_permutation刷力扣
这篇就一直更新一些C的选择题和编程题了。 目录 笔试题1 答案及解析1 笔试题2 答案及解析2 力扣编程题 88. 合并两个有序数组 解析代码 349. 两个数组的交集 解析代码 60. 排列序列 解析代码 46. 全排列 解析代码 本篇完。 笔试题1 1. 以下哪种STL容器中的对象…...
适用于Linux的Windows子系统(系统安装步骤)
目录 前言 一、WSL2安装 1.Microsoft参考文档(推荐选择旧版 WSL 的手动安装步骤) 2.开启子系统 二、Ubuntu安装 1.在Microsoft Store中获取ubuntu 2.运行ubuntu配置管理信息 3.ubuntu换源 三、WSL 与 Ubuntu的一些基础使用命令 四、Windows Terminal终端…...

HarmonyOS/OpenHarmony(Stage模型)应用开发组合手势(二)并行识别
并行识别组合手势对应的GestureMode为Parallel。并行识别组合手势中注册的手势将同时进行识别,直到所有手势识别结束。并行识别手势组合中的手势进行识别时互不影响。 以在一个Column组件上绑定点击手势和双击手势组成的并行识别手势为例,由于单击手势和…...
如何使用GPT引领前沿与应用突破之GPT4科研实践技术与AI绘图
GPT对于每个科研人员已经成为不可或缺的辅助工具,不同的研究领域和项目具有不同的需求。例如在科研编程、绘图领域: 1、编程建议和示例代码: 无论你使用的编程语言是Python、R、MATLAB还是其他语言,都可以为你提供相关的代码示例。 2、数据可…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...
)
LLaMA-Factory 微调 Qwen2-VL 进行人脸情感识别(二)
在上一篇文章中,我们详细介绍了如何使用LLaMA-Factory框架对Qwen2-VL大模型进行微调,以实现人脸情感识别的功能。本篇文章将聚焦于微调完成后,如何调用这个模型进行人脸情感识别的具体代码实现,包括详细的步骤和注释。 模型调用步骤 环境准备:确保安装了必要的Python库。…...

comfyui 工作流中 图生视频 如何增加视频的长度到5秒
comfyUI 工作流怎么可以生成更长的视频。除了硬件显存要求之外还有别的方法吗? 在ComfyUI中实现图生视频并延长到5秒,需要结合多个扩展和技巧。以下是完整解决方案: 核心工作流配置(24fps下5秒120帧) #mermaid-svg-yP…...

第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10+pip3.10)
第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10pip3.10) 一:前言二:安装编译依赖二:安装Python3.10三:安装PIP3.10四:安装Paddlepaddle基础框架4.1…...
