003传统图机器学习、图特征工程
文章目录
- 一. 人工特征工程、连接特征
- 二. 在节点层面对连接特征进行特征提取
- 三. 在连接层面对连接特征进行特征提取
- 四. 在全图层面对连接特征进行特征提取
一. 人工特征工程、连接特征
- 节点、连接、子图、全图都有各自的属性特征, 属性特征一般是多模态的。
- 除属性特征外,还有连接特征。本讲侧重点为:用人工特征提取的方法对连接特征进行提取。
二. 在节点层面对连接特征进行特征提取
- 节点的度:只看连接个数,不看连接质量。
- 节点的中心性:
- 特征向量中心性:其原理是某节点周围的节点都很重要,那么它也重要。
- 中介中心性:其原理是若某节点处于交通咽喉,那么它很重要。
- 邻接中心性:其原理是若一个节点去哪都近,那么它很重要。
- 节点的聚集系数:衡量节点周围的抱团程度,其实就是查以该节点为端点的三角形个数。
- Graphlets:聚集系数中的三角形结构可以视为一种子图,那么用其他子图代替三角形结构也是可以的,这就是Graphlets。提取某节点周围不同子图的个数,就可以构成一个向量Graphlet Degree Vector(GDV)。这个向量就可以用于描述节点的邻域拓扑结构信息。
- 还有其他的衡量方式如:PageRank、Katz中心性等。在NetworkX里包含多种数据挖掘算法可供使用。
三. 在连接层面对连接特征进行特征提取
- 即提取连接的特征,把连接变成 d 维向量。
- 基于两节点的距离:
- 两节点间最短路径长度:只看长度,忽略个数、质量。
- 基于两节点局部连接信息:
- 两节点共同相邻节点个数(交集)
- 两节点相邻节点的交并集合个数比
- Adamic-Adar index:
- S a = ∑ u ∈ N ( V 1 ) ∩ N ( V 2 ) 1 l o g ( k u ) S_{a}=\textstyle \sum_{u\in N(V_{1})\cap N(V_{2})}\frac{1}{log(k_{u})} Sa=∑u∈N(V1)∩N(V2)log(ku)1。
- 可以这样理解,两个人的连接若通过几个公众人物,那么他俩大概率不会很亲近。若通过一个普通人,那大概关系是不错的。
存在一个问题,如果两个节点没有共同的邻域节点,则以上三个指标都为 0 没有意义,这就需要看全图的信息了。
- 基于两节点在全图的连接信息——Katz index:
- 记录两节点间长度为k的路径个数。
- 其可以通过邻接矩阵的幂来求解。
- 设图的邻接矩阵为A,则节点u、v之间长度为k的路径个数是 A k A^{k} Ak矩阵的第u行第v列的值。
- 公式为 S u , v = ∑ l = 1 ∞ β l A u , v l = ( I − β A ) − 1 − I S_{u,v} = \sum_{l=1}^{\infty } \beta ^{l}A^{l}_{u,v}=(I-\beta A)^{-1}-I Su,v=∑l=1∞βlAu,vl=(I−βA)−1−I,其中 β \beta β是缩放因子,得到的是katz系数矩阵。
四. 在全图层面对连接特征进行特征提取
- 所得的特征应该能反映全图的结构特点。
- Bag-of-node-degrees:只看节点的度,不看连接结构 。实际上还是数数,数不同度对应的节点个数。
- Graphlet Kernel:
- 数 Graphlet 的个数得到 Bag-of-Graphlet,算是 Bag-of-* 的推广。
- 与节点层面不同从全图的角度 Graphlet 可以有孤立节点。
- 统计各种 Graphlet 的个数,也可以构成 d 维向量。
- 对两个图的 Bag-of-Graphlet 做归一化后,再做数量积就得到它俩的 Graphlet Kernel。
- 然而 Graphlet Kernel 计算复杂度过高,应用空间很小,引出Weisfeiler-Lehman Kernel。
- Weisfeiler-Lehman Kernel:
- 其特点是通过迭代不断丰富节点词库。
- 其用到的是颜色微调的方法。
- 通过多次迭代,进行节点颜色微调,丰富节点词库,最后统计不同颜色节点出现的次数,得到向量,实现特征提取。
- 对两个图的向量进行数量积运算,所得即 Weisfeiler-Lehman Kernel 。
- 一般迭代次数越多,效果越好。
- 注1:计算两个图的 Weisfeiler-Lehman Kernel 时,迭代计算要同时进行,即节点颜色词库要由两个图同时贡献。
- 注2:NetwokX 里的 weisfeiler_lehman_graph_hash 实现与上面说的不一样,gklearn.kernels.Weisfeilerlehmankernel 才是一样的。
相关文章:

003传统图机器学习、图特征工程
文章目录 一. 人工特征工程、连接特征二. 在节点层面对连接特征进行特征提取三. 在连接层面对连接特征进行特征提取四. 在全图层面对连接特征进行特征提取 一. 人工特征工程、连接特征 节点、连接、子图、全图都有各自的属性特征, 属性特征一般是多模态的。除属性特…...
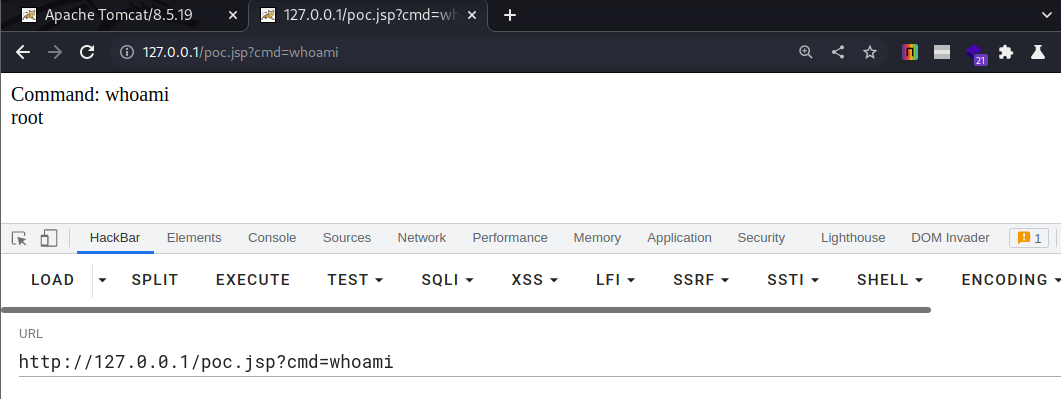
Apache Tomcat 漏洞复现
文章目录 Apache Tomcat 漏洞复现1. Tomcat7 弱密码和后端 Getshell 漏洞1.1 漏洞描述1.2 漏洞复现1.3 漏洞利用1.3.1 jsp小马1.3.2 jsp大马 1.4 安全加固 2. Aapache Tomcat AJP任意文件读取/包含漏洞2.1 漏洞描述2.1 漏洞复现2.2 漏洞利用工具2.4 修复建议 3. 通过 PUT 方法的…...

Oracle-常用权限-完整版
-- 创建用户 create user TCK identified by oracle; -- 赋权 grant connect,resource to TCK; -- 删除权限 revoke select any table from TCK -- 删除用户 CASCADE(用户下的数据级联删除) drop user TCK CASCADE -- 查询权限列表 select * from user_role_privs; select * fr…...
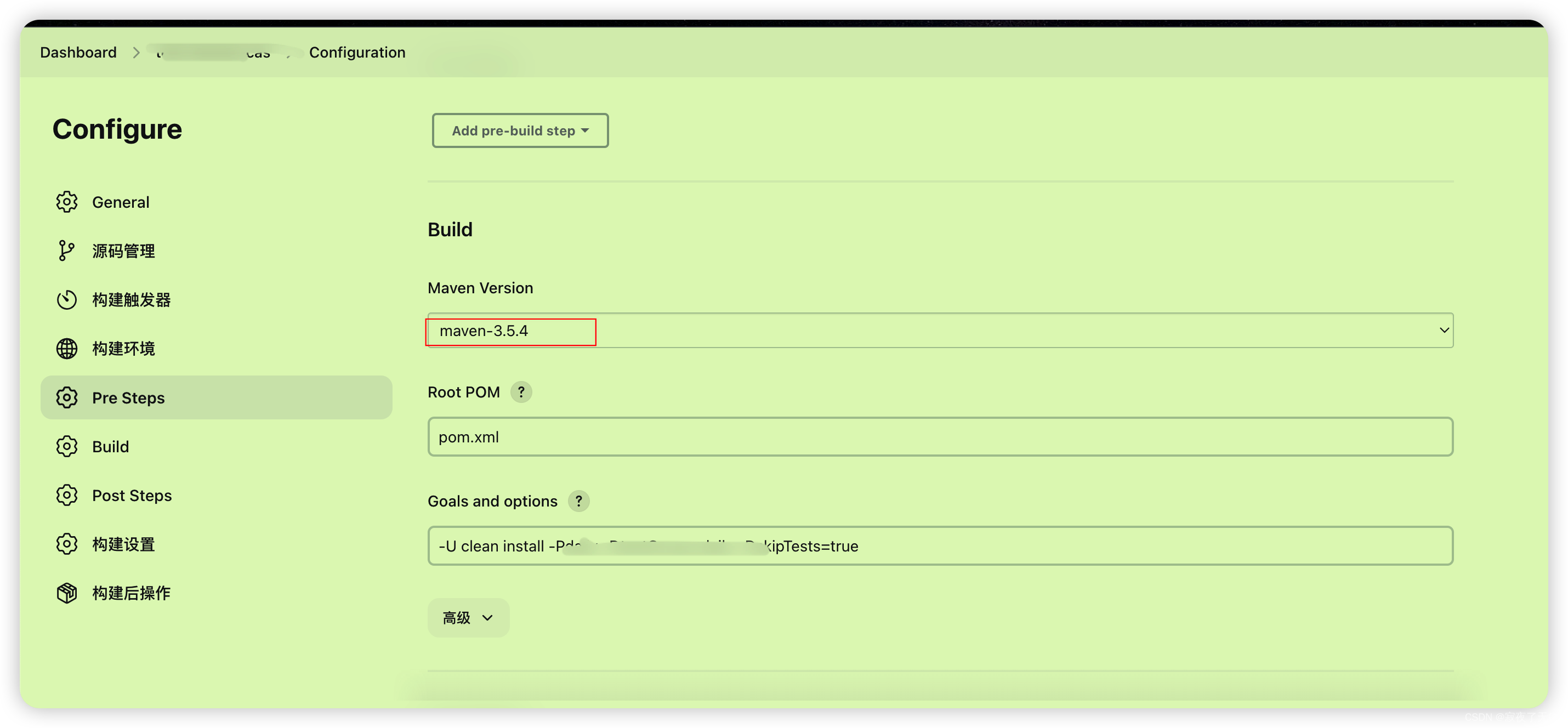
jenkins 发布job切换不同的jdk版本/ maven版本
1. 技术要求 因为有个新的项目需要使用jdk17 而旧的项目需要jdk1.8 这就需要jenkins在发布项目的时候可以指定jdk版本 2. 解决 jenkins全局工具配置页面 配置新的jdk 路径 系统管理-> 全局工具配置 如上新增个jdk 名称叫 jdk-17 然后配置jdk-17的根路径即可(这…...
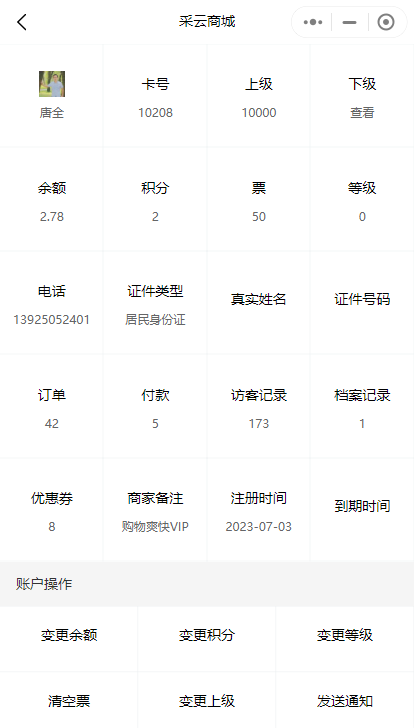
如何在小程序中给会员设置备注
给会员设置备注是一项非常有用的功能,它可以帮助商家更好地管理和了解自己的会员。下面是一个简单的教程,告诉商家如何在小程序中给会员设置备注。 1. 找到指定的会员卡。在管理员后台->会员管理处,找到需要设置备注的会员卡。也支持对会…...
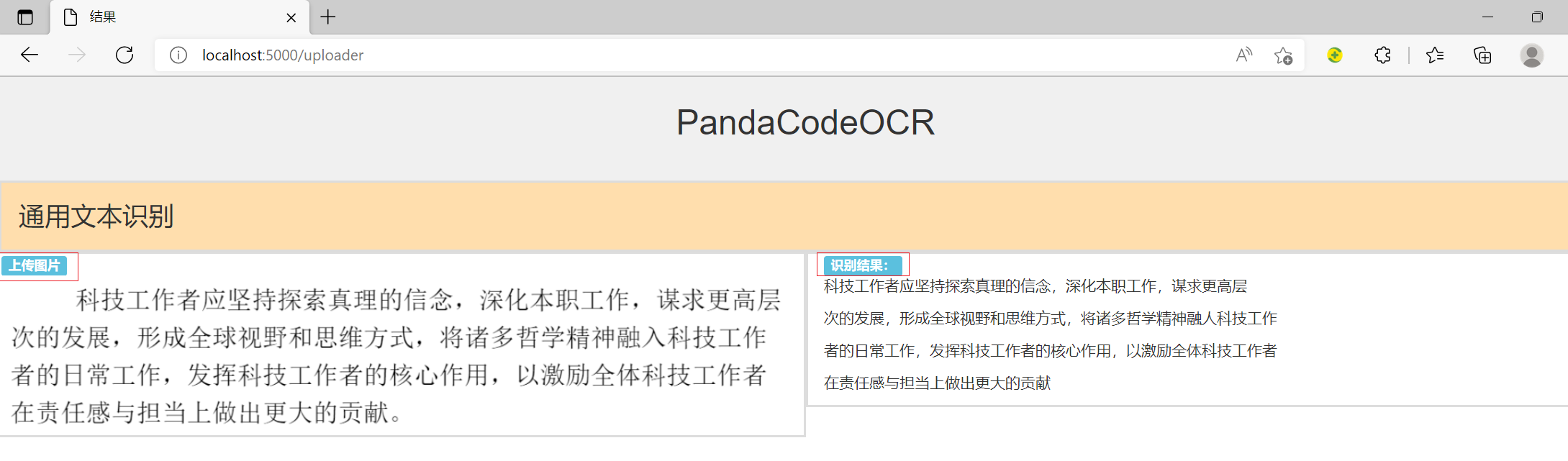
PaddleOCR学习笔记2-初步识别服务
今天初步实现了网页,上传图片,识别显示结果到页面的服务。后续再完善。 采用flask paddleocr bootstrap快速搭建OCR识别服务。 代码结构如下: 模板页面代码文件如下: upload.html : <!DOCTYPE html> <html> <…...

【Opencv】Pyhton 播放上一帧,下一帧,存video,逐帧分析
文章目录 读取具体哪一帧等待按钮写入解码方式与文件格式对应全部代码 读取具体哪一帧 这个方法可以获取某一帧: while True:cap.set(cv2.CAP_PROP_POS_FRAMES, current_frame)ret, frame cap.read()if not ret:break等待按钮 这个方法可以显示当前帧,…...
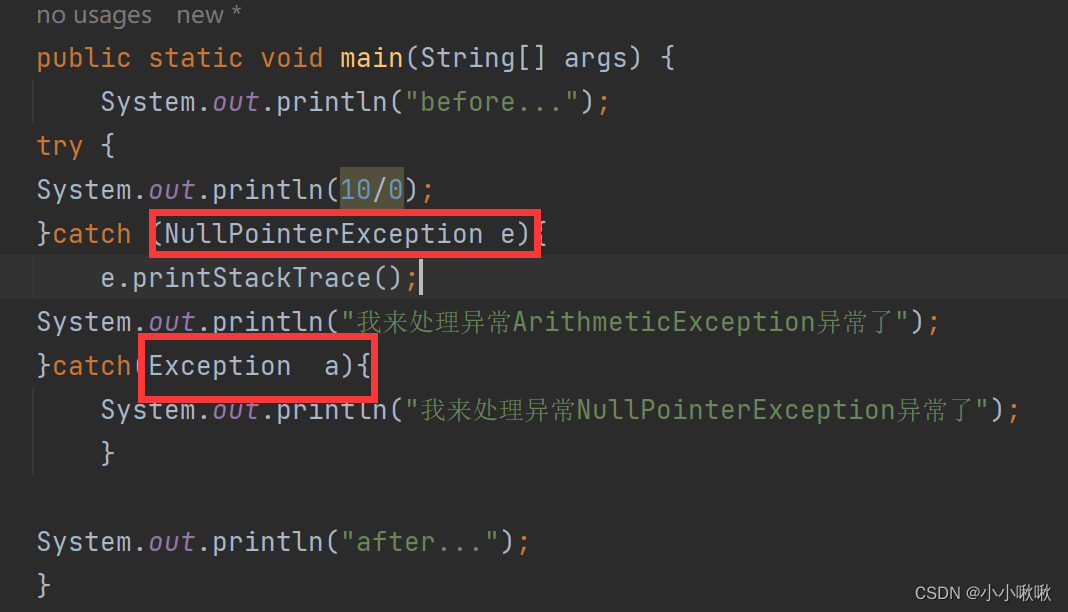
【关于Java:认识异常】
文章目录 一、1. 异常概念与体系结构1.1 异常的概念1.2 常见的异常1.算数异常2.数组越界异常3.空指针异常 1.3 异常的体系结构1.4 异常的分类1. 编译时异常2. 运行时异常(RuntimeException) 二、 异常的处理方式2.1 防御式编程2.2 EAFP:(异常…...

【C++ • STL • 力扣】详解string相关OJ
文章目录 1、仅仅翻转字母2、字符串中的第一个唯一字符3、字符串里最后一个单词的长度4、验证一个字符串是否是回文5、字符串相加总结 ヾ(๑╹◡╹)ノ" 人总要为过去的懒惰而付出代价 ヾ(๑╹◡╹)ノ" 1、仅仅翻转字母 力扣链接 代码1展示&…...
【Tomcat服务部署及优化】
Tomcat 一、什么是Tomcat?二、Tomcat 核心组件2.1 Tomcat 组件2.3 Container组件的结构2.4 Tomcat 请求过程 三、Tomcat 部署3.1 安装JDK3.2 设置JDK环境变量3.3 安装Tomcat并用supervisor启动解压添加到supervisord服务测试能否通过supervisorctl启动 四、Tomcat的端口和主要…...
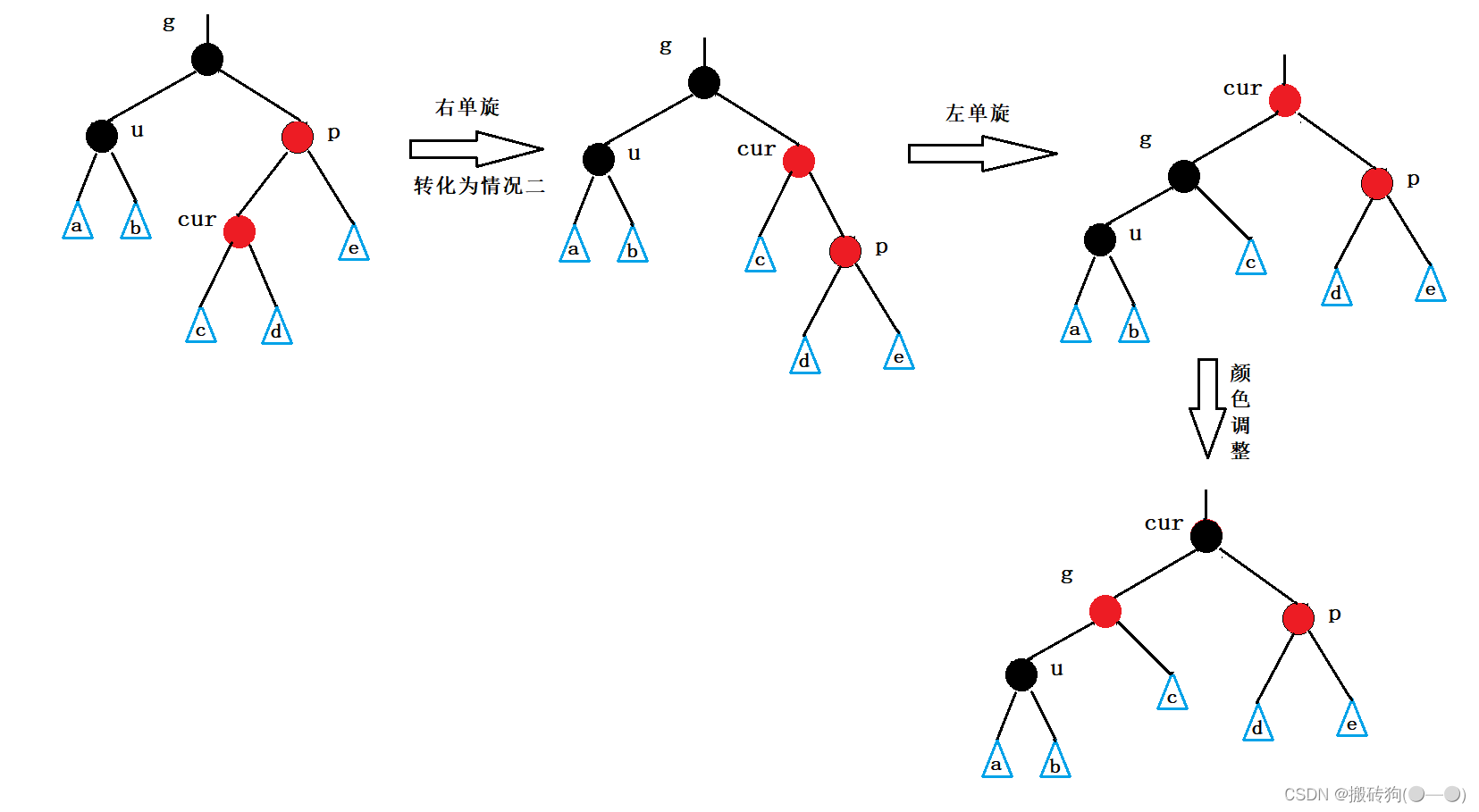
C++之红黑树
红黑树 红黑树的概念红黑树的性质红黑树结点的定义红黑树的插入红黑树的验证红黑树与AVL树的比较 红黑树的概念 红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。 通过对任何一条从根到叶子的路径上…...
TCP)
Go语言网络编程(socket编程)TCP
1、TCP编程 1.1.1 Go语言实现TCP通信 TCP协议 TCP/IP(Transmission Control Protocol/Internet Protocol) 即传输控制协议/网间协议,是一种面向连接(连接导向)的、可靠的、基于字节流的传输层(Transport layer)通信协…...

C语言——局部和全局变量
局部变量 定义在函数内部的变量称为局部变量(Local Variable) 局部变量的作用域(作用范围)仅限于函数内部, 离开该函数后是无效的 离开该函数后,局部变量自动释放 示例代码: #include <stdio.h>// 函数定义 …...
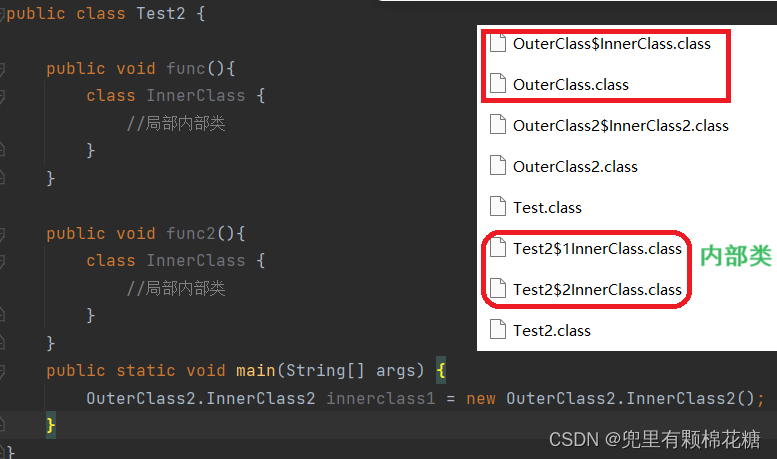
【Java基础篇 | 类和对象】--- 聊聊什么是内部类
个人主页:兜里有颗棉花糖 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 兜里有颗棉花糖 原创 收录于专栏【JavaSE_primary】 本专栏旨在分享学习Java的一点学习心得,欢迎大家在评论区讨论💌 前言 当一个事物的内部&…...

合宙Air724UG LuatOS-Air LVGL API控件-页面 (Page)
页面 (Page) 当控件内容过多,无法在屏幕内完整显示时,可让其在 页面 内显示。 示例代码 page lvgl.page_create(lvgl.scr_act(), nil) lvgl.obj_set_size(page, 150, 200) lvgl.obj_align(page, nil, lvgl.ALIGN_CENTER, 0, 0)label lvgl.label_crea…...
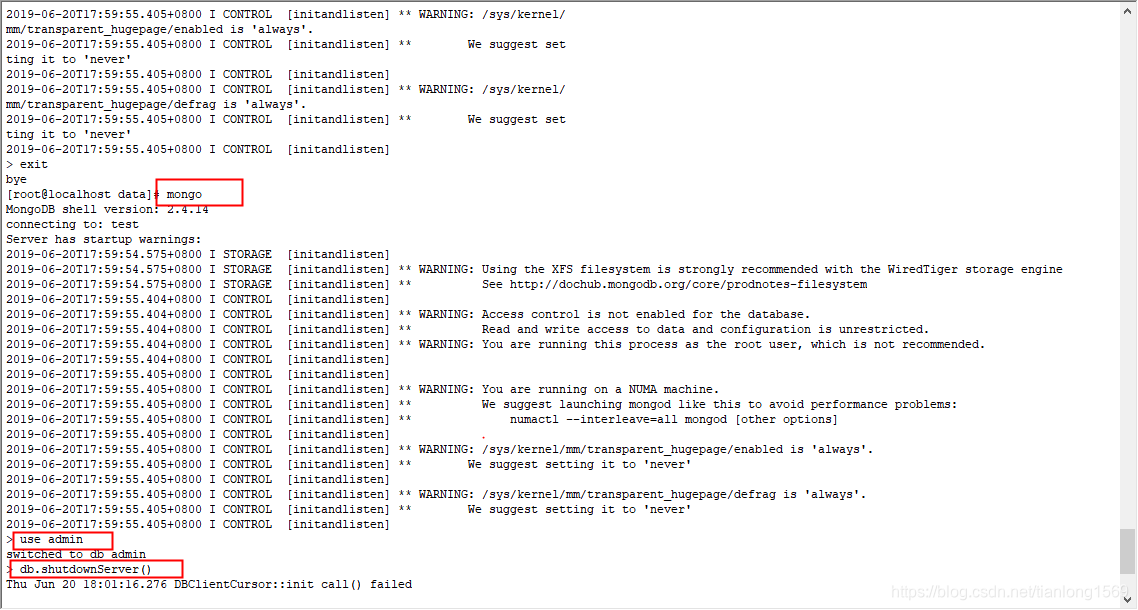
mongodb数据库操作
1、启动mongodb /usr/local/mongodb/bin/mongod --dbpath /var/mongodb/data/--logpath /var/mongodb/logs/log.log &在mongodb启动命令中 --dbpath 指定mongodb的数据存储路径 --logpath 指定mongodb的日志存储路径 2、停止mongodb 第一步先进入mongo命令行模式 第二…...
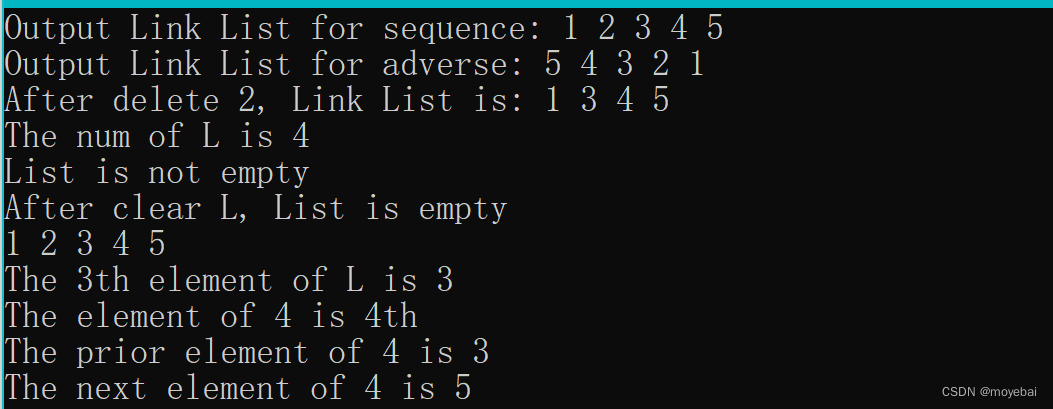
第 2 章 线性表 ( 双链循环线性表(链式存储结构)实现)
1. 背景说明 2. 示例代码 1) status.h /* DataStructure 预定义常量和类型头文件 */#ifndef STATUS_H #define STATUS_H#define CHECK_NULL(pointer) if (!(pointer)) { \printf("FuncName: %-15s Line: %-5d ErrorCode: %-3d\n", __func__, __LINE__, ERR_NULL_PTR…...

redis在日常开发工作中的常见用法
redis是一款内存型数据库,在开发工作中经常用到,功能强大; 特别开一篇文章用来记录一下它的常见用法,算是一种总结; 它最主要的特点就是高可用的,速度快,分布式;有人说速度快&…...

小程序实现下拉刷新
小程序实现下拉刷新可以通过使用组件scroll-view和事件onPullDownRefresh来实现。 scroll-view组件的使用 在需要下拉刷新的页面的wxml文件中,通过scroll-view组件包裹需要滚动的内容,设置scroll-y属性为true,表示允许竖向滚动。示例代码如…...

Day 36 贪心算法 part05 : 435. 无重叠区间 763.划分字母区间 56. 合并区间
56. 合并区间 以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。 示例 1: 输入:inte…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

论文阅读笔记——Muffin: Testing Deep Learning Libraries via Neural Architecture Fuzzing
Muffin 论文 现有方法 CRADLE 和 LEMON,依赖模型推理阶段输出进行差分测试,但在训练阶段是不可行的,因为训练阶段直到最后才有固定输出,中间过程是不断变化的。API 库覆盖低,因为各个 API 都是在各种具体场景下使用。…...

数据结构:递归的种类(Types of Recursion)
目录 尾递归(Tail Recursion) 什么是 Loop(循环)? 复杂度分析 头递归(Head Recursion) 树形递归(Tree Recursion) 线性递归(Linear Recursion)…...

全面解析数据库:从基础概念到前沿应用
在数字化时代,数据已成为企业和社会发展的核心资产,而数据库作为存储、管理和处理数据的关键工具,在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理,到社交网络的用户数据存储,再到金融行业的交易记录处理&a…...

C# winform教程(二)----checkbox
一、作用 提供一个用户选择或者不选的状态,这是一个可以多选的控件。 二、属性 其实功能大差不差,除了特殊的几个外,与button基本相同,所有说几个独有的 checkbox属性 名称内容含义appearance控件外观可以变成按钮形状checkali…...

Linux操作系统共享Windows操作系统的文件
目录 一、共享文件 二、挂载 一、共享文件 点击虚拟机选项-设置 点击选项,设置文件夹共享为总是启用,点击添加,可添加需要共享的文件夹 查询是否共享成功 ls /mnt/hgfs 如果显示Download(这是我共享的文件夹)&…...
