深度优先搜索遍历与广度优先搜索遍历
目录
一.深度优先搜索遍历
1.深度优先遍历的方法
2.采用邻接矩阵表示图的深度优先搜索遍历
3.非连通图的遍历
二.广度优先搜索遍历
1.广度优先搜索遍历的方法
2.非连通图的广度遍历
3.广度优先搜索遍历的实现
4.按广度优先非递归遍历连通图
一.深度优先搜索遍历
1.深度优先遍历的方法
从图中一个未访问的顶点V开始,沿着一条路一直走到底,如果到达这条路尽头的节点 ,则回退到上一个节点,再从另一条路开始走到底…,不断递归重复此过程,直到所有的顶点都遍历完成。
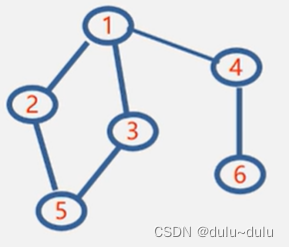
以下面无向图为例,2为起点
(1)以2为起点访问1
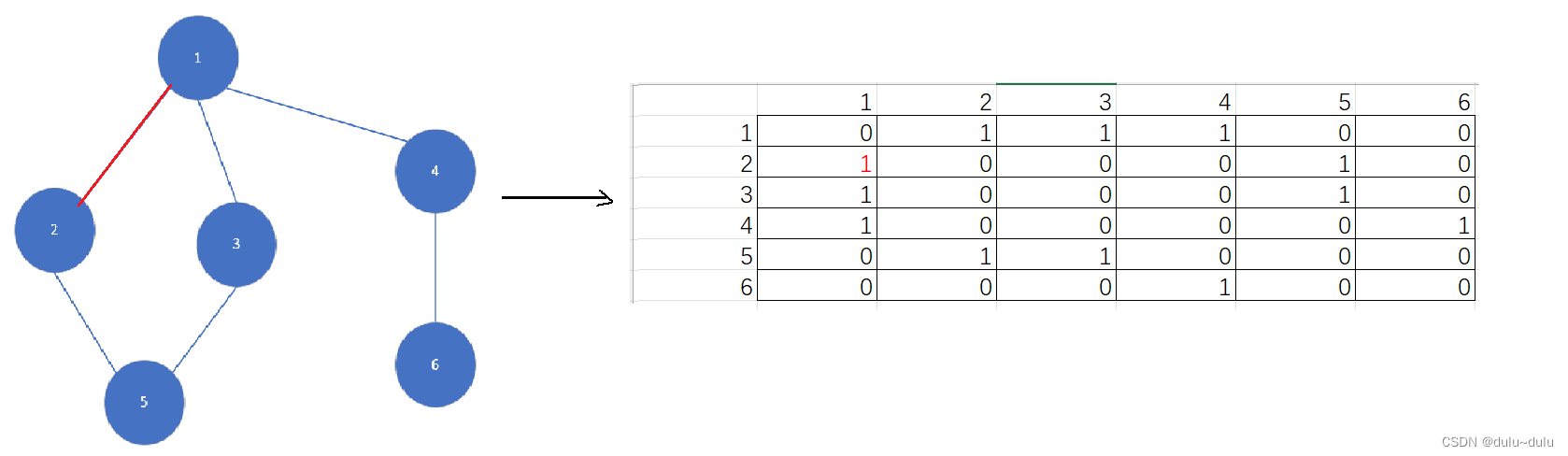
(2)以1为起点,因为“1”和“2”之间的边已经走过,所以走3
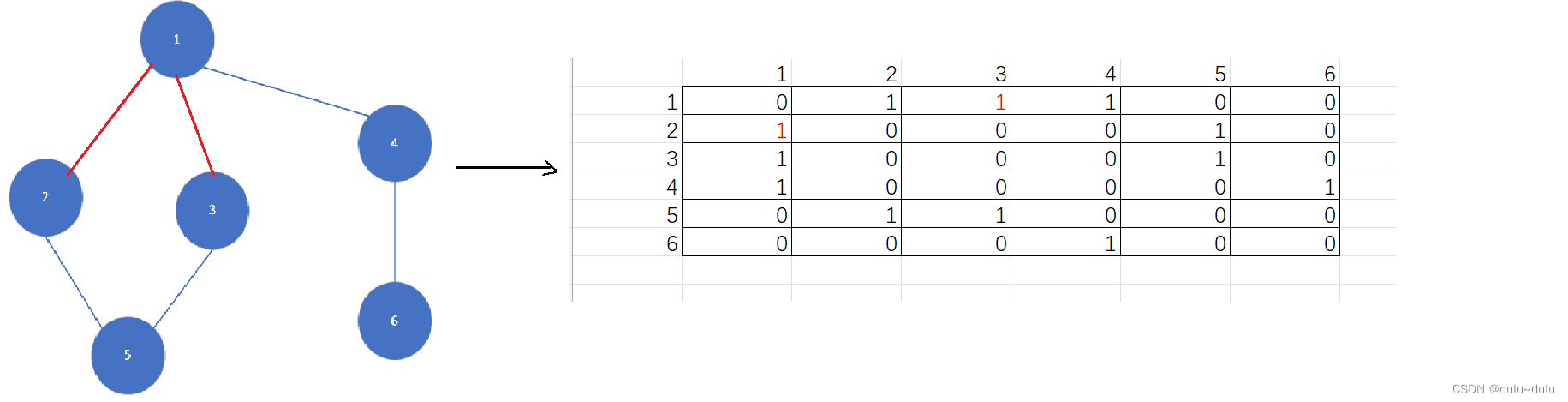
(3) 同理,以3为起点访问5
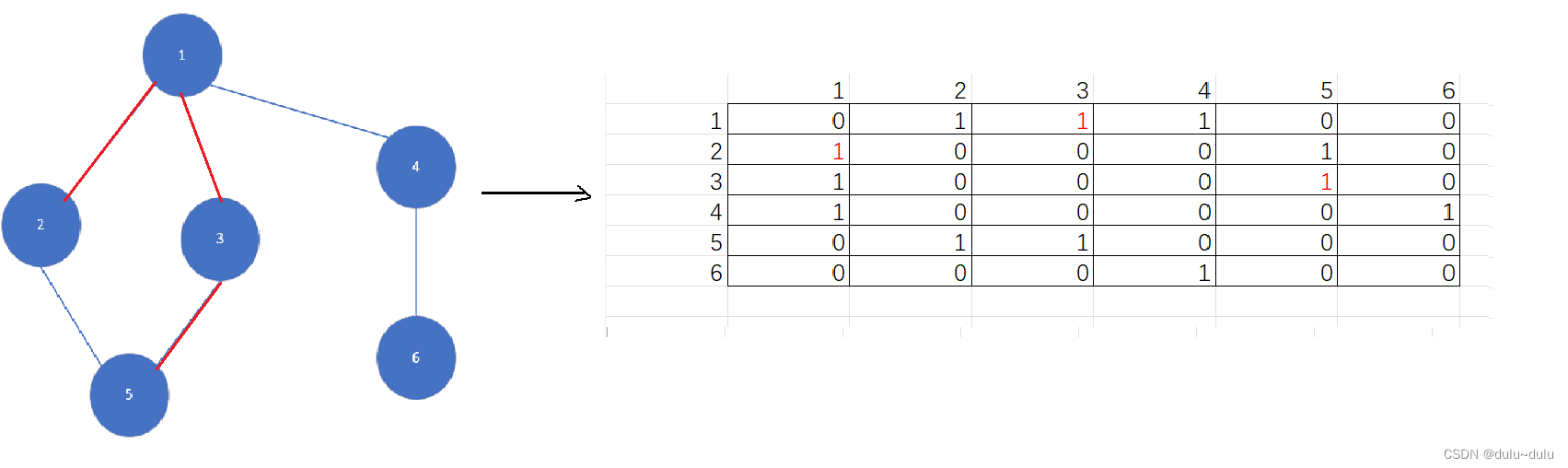
(4)到5后,没有可访问的点,返回3,3也没有可访问的点,到1后,可访问之前没有访问过的4
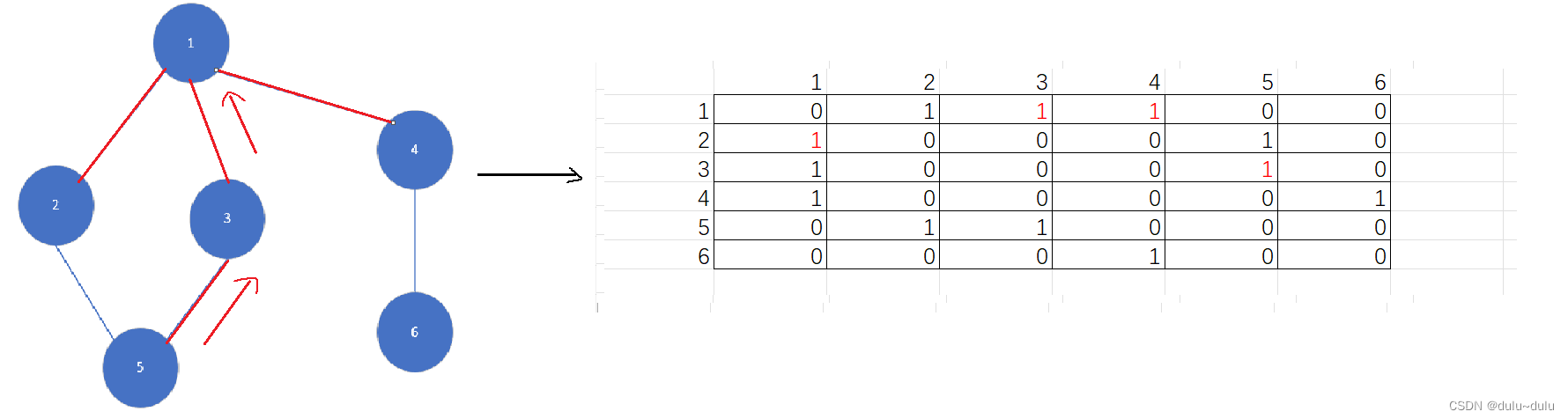
(5)4访问6,至此,遍历完所有的点,DFS(深度优先搜索遍历):2->1->3->5->4->6
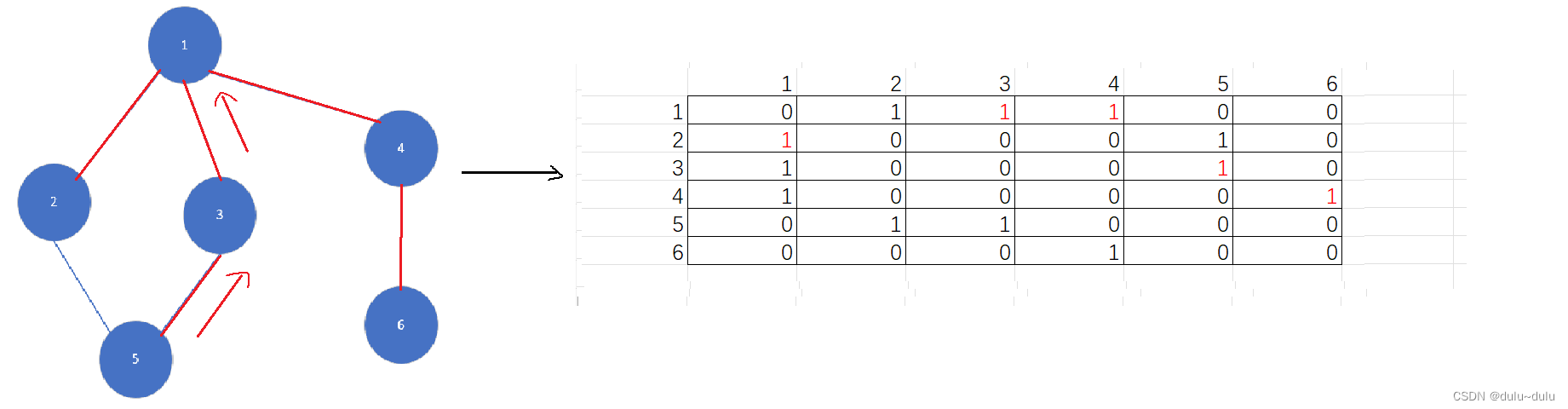
2.采用邻接矩阵表示图的深度优先搜索遍历
#define MAX_VERTEX_NUM 100typedef struct {// 定义图的相关信息int vexnum; // 顶点数int arcs[MAX_VERTEX_NUM][MAX_VERTEX_NUM]; // 邻接矩阵// 其他成员...
} AMSGraph;bool visited[MAX_VERTEX_NUM]; // 记录顶点是否被访问过void DFS(AMSGraph G, int v)
{cout << v;visited[v] = true;for (int w = 0; w < G.vexnum; w++) {if (G.arcs[v][w] == 1 && !visited[w]) {DFS(G, w);}}
}http://t.csdn.cn/HmcOt
之前的一篇文章已经详细说明了邻接矩阵和邻接表的区别,这里同理
1.用邻接矩阵表示图,遍历图中每一个顶点都要从头扫描该顶点所在行,时间复杂度O(
)
2.用邻接表表示图,虽然有2e个表结点,但只需扫描e个结点即可完成遍历,加上访问n个头结点的时间,时间复杂度为O(n+e)
•稠密图适于在邻接矩阵上进行深度遍历;
•稀疏图适于在邻接表上进行深度遍历。
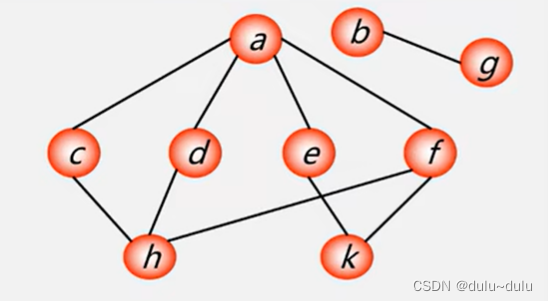
3.非连通图的遍历
左边的连通分量进行深度优先搜索遍历,再在b,g之中选择一个点进行深度优先搜索遍历
其中一种合理的顶点访问次序为:
a,c,h,d,f,k,e,b,g
二.广度优先搜索遍历
1.广度优先搜索遍历的方法
从某个顶点V出发,访问该顶点的所有邻接点V1,V2..VN,从邻接点V1,V2...VN出发,再访问他们各自的所有邻接点,重复上述步骤,直到所有的顶点都被访问过
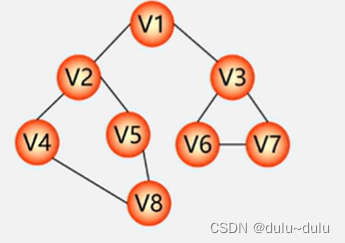
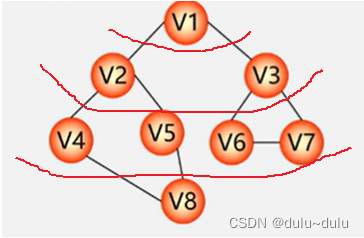
以如下图为例,起点为V1
一层一层进行访问,广度优先搜索遍历的结果为:V1->C2->V3->V4->V5->V6->V7->V8
2.非连通图的广度遍历
与连通图类似,在b,g中任意选择一个点开始
合理的顶点访问次序为:a->c->d->e->f->h->k->b->g

3.广度优先搜索遍历的实现
广度优先搜索遍历的实现,与树的层次遍历很像,可以用队列进行实现(出队一个结点,将他的邻接结点入队)
以下动图来自爱编程的西瓜,方便大家理解遍历过程
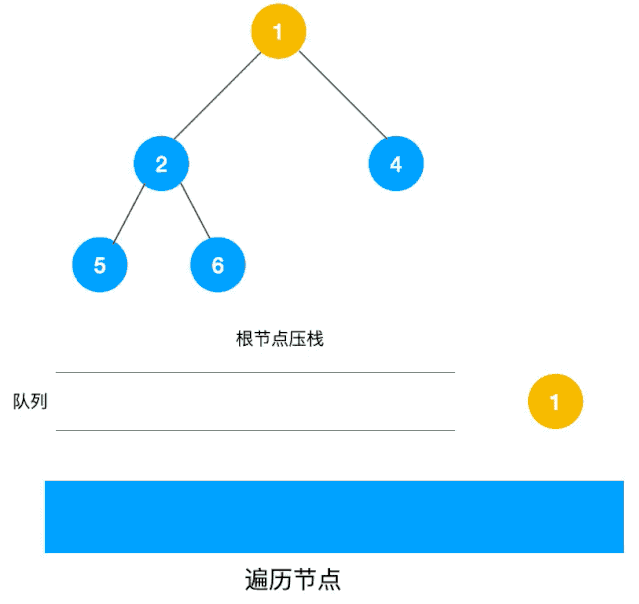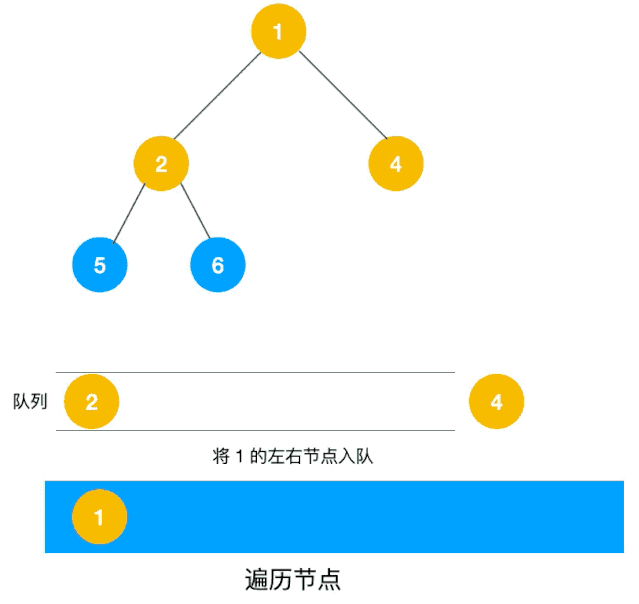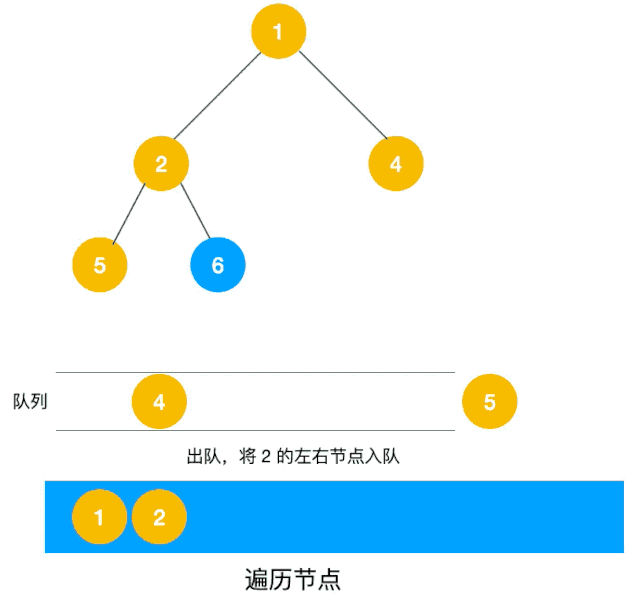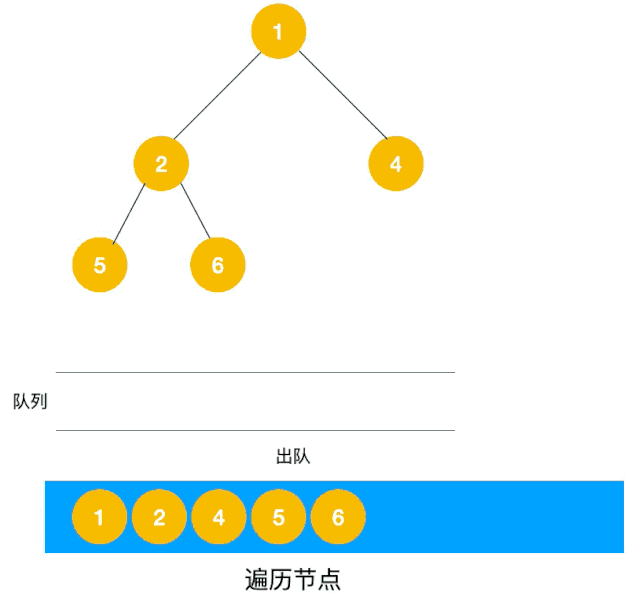
4.按广度优先非递归遍历连通图
#include <iostream>
using namespace std;const int MAX_SIZE = 100; // 队列的最大容量
const int MAX_VERTICES = 100; // 图的最大顶点数struct Queue {int data[MAX_SIZE];int front; // 队头指针int rear; // 队尾指针
};struct Graph { // 定义图bool edges[MAX_VERTICES][MAX_VERTICES]; // 邻接矩阵int numVertices; // 实际顶点数
};void InitQueue(Queue& Q) {Q.front = 0;Q.rear = -1;
}bool EnQueue(Queue& Q, int x) {if (Q.rear == MAX_SIZE - 1) {// 队列已满,无法插入return false;}Q.data[++Q.rear] = x;return true;
}bool DeQueue(Queue& Q, int& x) {if (Q.front > Q.rear) {// 队列为空,无法出队return false;}x = Q.data[Q.front++];return true;
}bool QueueEmpty(Queue& Q) {return Q.front > Q.rear;
}// 找到顶点u的第一个邻接点并返回
int FirstAdjVex(Graph& G, int u) {for (int v = 0; v < G.numVertices; ++v) {if (G.edges[u][v]) {return v;}}return -1; // 或者返回一个特殊的值表示找不到邻接点
}// 找到图 G 中顶点 u 相对于顶点 w 的下一个邻接点并返回
int NextAdjVex(Graph& G, int u, int w) {for (int v = w + 1; v < G.numVertices; ++v) {if (G.edges[u][v]) {return v;}}return -1; // 或者返回一个特殊的值表示找不到下一个邻接点
}void BFS(Graph G, int v) {cout << v;bool visited[MAX_VERTICES] = { false };visited[v] = true; // 访问第v个顶点Queue Q;InitQueue(Q);EnQueue(Q, v); // v进队while (!QueueEmpty(Q)) {int u;DeQueue(Q, u); // 队头元素出队并置为ufor (int w = FirstAdjVex(G, u); w >= 0; w = NextAdjVex(G, u, w)) {if (!visited[w]) { // w为u的尚未访问的邻接点cout << w;visited[w] = true;EnQueue(Q, w); // w进队(将访问的每一个邻接点入队)}}}
}
广度优先搜索遍历算法的效率
1.如果使用邻接矩阵,则BFS对于每一个被访问到的顶点,都要循环检测矩阵中的整整一行,时间复杂度为O()
2.用邻接表来表示图,虽然有2e个表结点,但只需扫描e个结点即可完成遍历,加上访问n个头结点的实践,时间复杂度为O(n+e)
深度优先搜索遍历(DFS)与广度优先搜索遍历(BFS)算法的效率
1.空间复杂度相同,都是O(n)(借用了堆栈或队列)
2.时间复杂度只与存储结构(邻接矩阵【O()】或邻接表【O(n+e)】)有关,而与搜索路径无关
相关文章:
深度优先搜索遍历与广度优先搜索遍历
目录 一.深度优先搜索遍历 1.深度优先遍历的方法 2.采用邻接矩阵表示图的深度优先搜索遍历 3.非连通图的遍历 二.广度优先搜索遍历 1.广度优先搜索遍历的方法 2.非连通图的广度遍历 3.广度优先搜索遍历的实现 4.按广度优先非递归遍历连通图 一.深度优先搜索遍历 1.深…...

java 中 返回一个空Map
原文链接:Map用法总结 Constructs an empty HashMap with the default initial capacity (16) (mutable) // Constructs an empty HashMap with the default initial capacity (16) and the default load fact // Since:1.2 Map<String, …...

sql 执行插入多条语句中 n个insert 与 一个insert+多个values 性能上有和区别 -- chatGPT
在 SQL 中,你可以使用多种方式来插入多条记录。其中两种常见的方式是: 1. **多个 INSERT 语句**:每个 INSERT 语句都插入一行记录。 sql INSERT INTO table_name (column1, column2, ...) VALUES (value1_1, value1_2, ...); INSERT INTO …...

数学建模国赛C蔬菜类商品的自动定价与补货决策C
数学建模国赛C蔬菜类商品的自动定价与补货决策C 完整思路和代码请私信~~~ 1.拟解决问题 这是一个关于生鲜商超蔬菜商品管理的复杂问题,需要综合考虑销售、补货、定价等多个方面。以下是对这些问题的总结: 问题 1: 蔬菜销售分析 需要分析蔬菜各品类和…...
的重要性)
在程序开发中,接口(interface)的重要性
开了很多人写的程序,都适用了接口,也适用了注入,也没有感到什么不妥。如果只是为了注入而写接口,其实我感觉大可不必,特别是把接口和实体写在一个项目项目中的。 我不知道其他人怎么看接口这一层,接口最大的…...

MyBatis关联关系映射详解
前言 在使用MyBatis进行数据库操作时,关联关系映射是一个非常重要的概念。它允许我们在数据库表之间建立关联,并通过对象之间的关系来进行数据查询和操作。本文将详细介绍MyBatis中的关联关系映射,包括一对一、一对多和多对多关系的处理方法…...
常用电子元器件基础知识
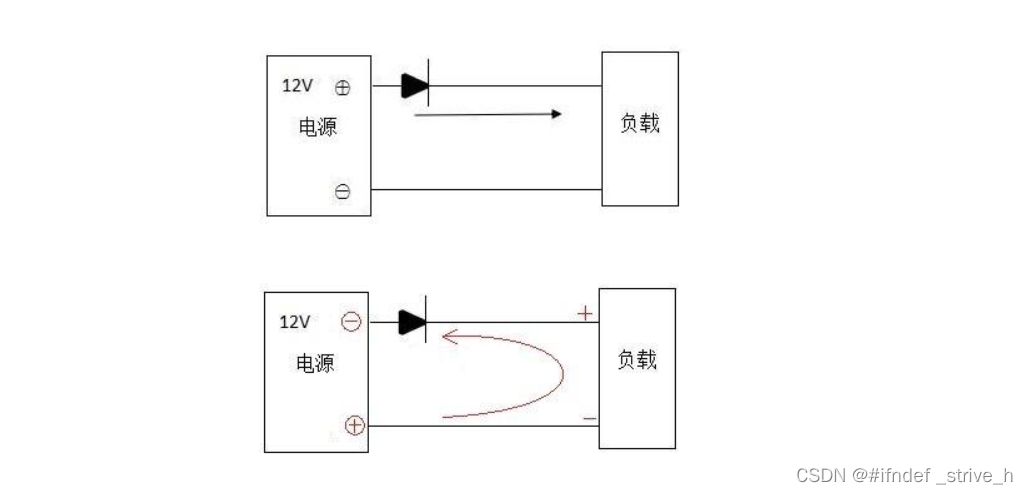
目录 一、电阻 二、电容 三、电感 四、保险丝 五、二极管 一、电阻 概念:顾名思义,就是增加电流通过的阻力的。 就像是在水渠中放入东西,能阻止水的顺利通过也是一个道理。 基于电阻的电气特性,电阻在电路中主要有以下四个…...
git撤销还未push的的提交
怎样撤销掉上图中的提交呢 使用以下代码即可提交 git reset --soft HEAD^...

MySQL--数据库基础
数据库分类 数据库大体可以分为 关系型数据库 和 非关系型数据库 常用数据类型 数值类型: 分为整型和浮点型: 字符串类型 日期类型...
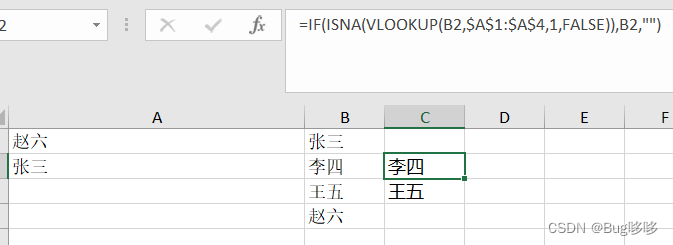
Excel相关笔记
1、找出B列中A列没有的数据并放在C列 公式:IF(ISNA(VLOOKUP(B1,$A 1 : 1: 1:A$4,1,FALSE)),B1,“”)...
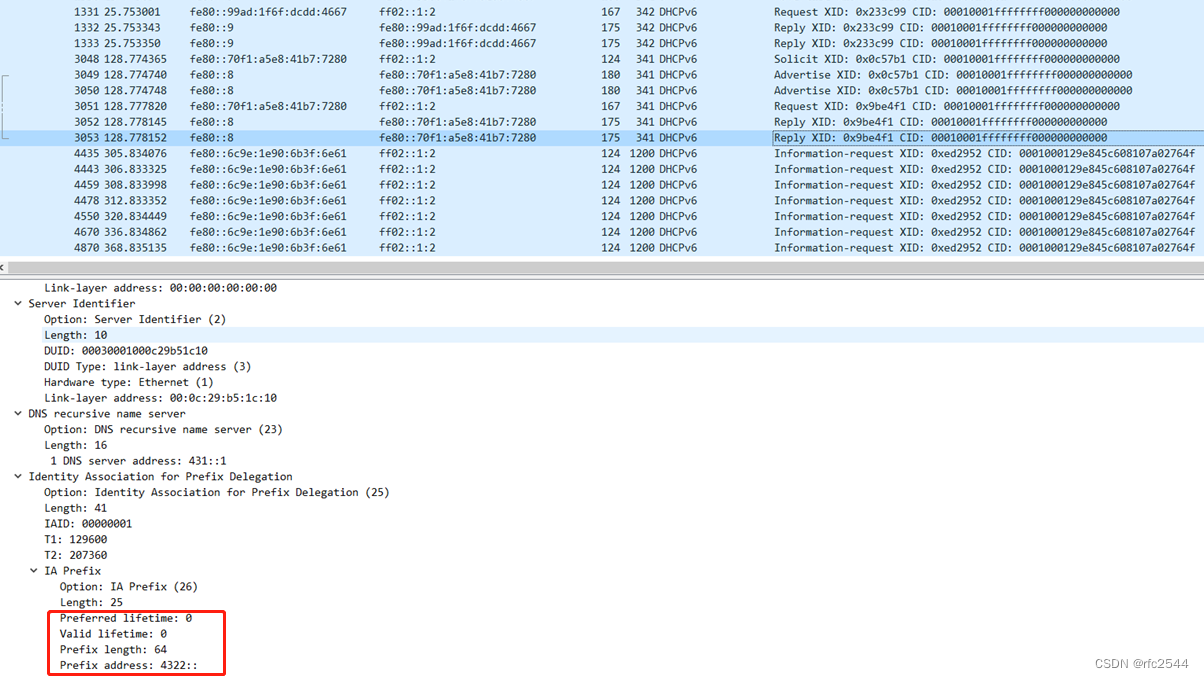
RouterOS-配置PPPoEv4v6 Server
1 接口 ether3 出接口 ether4 内网接口 2 出接口 出接口采用PPPoE拨号SLAAC获取前缀,手动配置后缀 2.1 选择出接口interface,配置PPPoE client模式 2.2 配置PPPoE client用户名和密码 2.3 从PPPoE client获取前缀地址池 2.4 给出接口选择前缀并配置…...

PhpStorm软件安装包分享(附安装教程)
目录 一、软件简介 二、软件下载 一、软件简介 PhpStorm是一款由JetBrains开发的专业PHP集成开发环境(IDE),旨在提供全面的PHP开发支持。它是基于IntelliJ IDEA平台构建的,具有强大的功能和工具,可以帮助开发人员提高…...

JavaScript设计模式(三)——单例模式、装饰器模式、适配器模式
个人简介 👀个人主页: 前端杂货铺 🙋♂️学习方向: 主攻前端方向,正逐渐往全干发展 📃个人状态: 研发工程师,现效力于中国工业软件事业 🚀人生格言: 积跬步…...

LeetCode:有序数组的平方
题目 给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。 示例 1: 输入:nums [-4,-1,0,3,10] 输出:[0,1,9,16,100] 解释:平方后,数组变…...

数学分析:势场
首先从散度的物理解释开始。首先,在球内的向量场的散度的积分,等于它在球边界上的流量的积分。所以根据积分中值定理,我们可以这么理解散度,它就是这个体积内的速度场的平均密度。而速度场只和源有关,所以它表示的某个…...

MySQL 中 MyISAM 与 InnoDB 引擎的区别
分析&回答 区别很多,大家说出下面几点,面试就应该 OK 了 1) 事务支持 MyISAM不支持事务,而InnoDB支持。InnoDB的AUTOCOMMIT默认是打开的,即每条SQL语句会默认被封装成一个事务,自动提交,这样会影响速…...
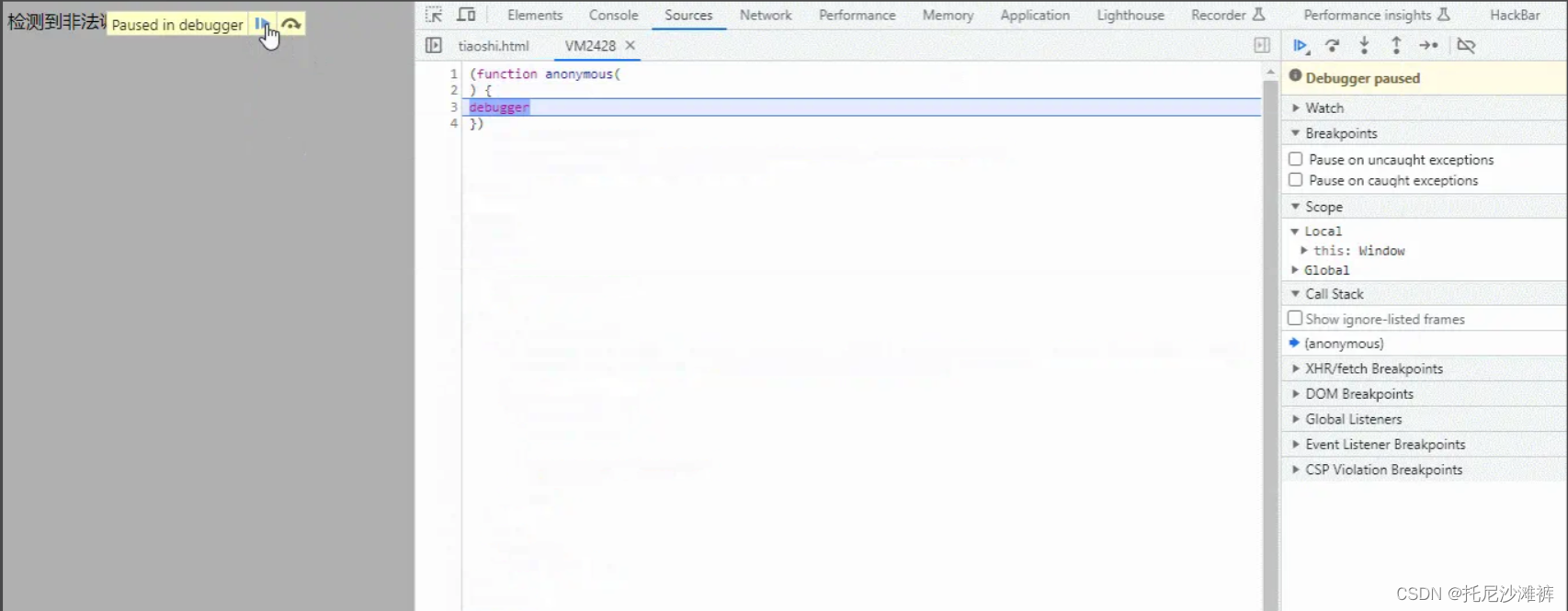
【javascript】禁止浏览器调试前端页面
目录 为啥要禁止?无限 debugger基础禁止调试解决对策 为啥要禁止? 由于前端页面会调用很多接口,有些接口会被别人爬虫分析,破解后获取数据,为了杜绝这种情况,最简单的方法就是禁止人家调试自己的前端代码 …...
 的过程)
Oracle Non-CDB配置 TDE(透明数据加密) 的过程
说明 此文档虽然是针对non CDB而写,但是对于CDB的操作过程也是类似的,即在CDB$ROOT中设置完成wallet设置后,在PDB中设置和打开MEK即可。 先决条件 请确保目录$ORACLE_SID/admin/$ORACLE_SID存在,例如此目录为: /u01/app/oracl…...

MySQL——常见问题
NULL和空值的区别 1、空值不占空间,NULL值占空间。当字段不为NULL时,也可以插入空值。 2、当使用 IS NOT NULL 或者 IS NULL 时,只能查出字段中没有不为NULL的或者为 NULL 的,不能查出空值。 3、判断NULL 用IS NULL 或者 is no…...
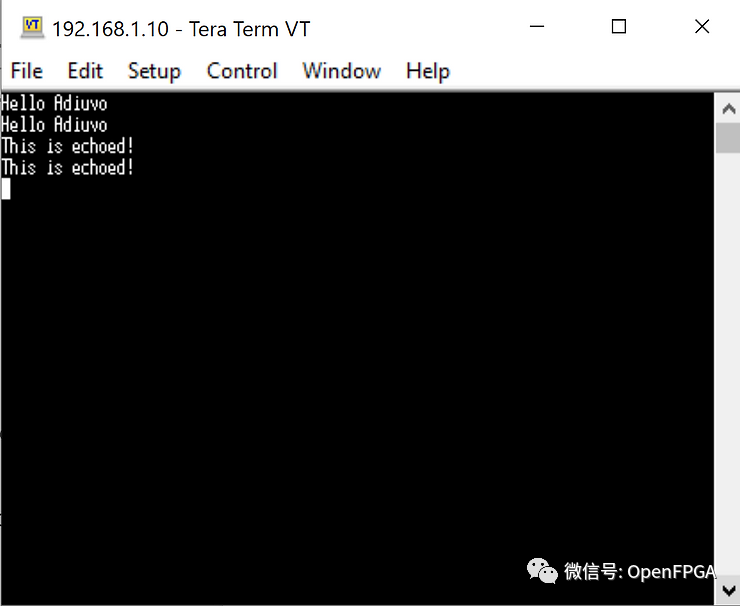
在FPGA上快速搭建以太网
在本文中,我们将介绍如何在FPGA上快速搭建以太网 (LWIP )。为此,我们将使用 MicroBlaze 作为主 CPU 运行其应用程序。 LWIP 是使用裸机设计以太网的良好起点,在此基础上我们可以轻松调整软件应用程序以提供更详细的应用…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...

五子棋测试用例
一.项目背景 1.1 项目简介 传统棋类文化的推广 五子棋是一种古老的棋类游戏,有着深厚的文化底蕴。通过将五子棋制作成网页游戏,可以让更多的人了解和接触到这一传统棋类文化。无论是国内还是国外的玩家,都可以通过网页五子棋感受到东方棋类…...

高考志愿填报管理系统---开发介绍
高考志愿填报管理系统是一款专为教育机构、学校和教师设计的学生信息管理和志愿填报辅助平台。系统基于Django框架开发,采用现代化的Web技术,为教育工作者提供高效、安全、便捷的学生管理解决方案。 ## 📋 系统概述 ### 🎯 系统定…...

rm视觉学习1-自瞄部分
首先先感谢中南大学的开源,提供了很全面的思路,减少了很多基础性的开发研究 我看的阅读的是中南大学FYT战队开源视觉代码 链接:https://github.com/CSU-FYT-Vision/FYT2024_vision.git 1.框架: 代码框架结构:readme有…...