机器学习——boosting之提升树
提升树和adaboost基本流程是相似的
我看到提升树的时候,懵了
这…跟adaboost有啥区别???
直到看到有个up主说了,我才稍微懂

相当于,我在adaboost里的弱分类器,换成CART决策树就好了呗?
书上也没有明说,唉。。。
还好,有大神提升树的具体讲解
看出来了,提升树主要是做二叉树分类和回归的:
- 如果是处理分类问题,弱分类器用CART决策树,就是adaboost了
- 如果是处理回归问题,弱分类器也是用CART决策树
- 每个新的弱分类器都是降低残差
1. 推导过程
-
建立提升树的加法模型
- 假设构成第i个弱分类器的参数为 θ i θ_i θi,第i个弱分类器则表示为 T ( x , θ i ) T(x,θ_i) T(x,θi)
- 当前弱分类器若表示为 T ( x , θ m ) T(x,θ_m) T(x,θm),强分类器则表示为: f m ( x ) = f m − 1 ( x ) + T ( x , θ m ) f_m(x) = f_{m-1}(x)+T(x,θ_m) fm(x)=fm−1(x)+T(x,θm)
- 预测结果为 y p r e = f m ( x ) = f m − 1 ( x ) + T ( x , θ m ) y_{pre}=f_m(x)=f_{m-1}(x)+T(x,θ_m) ypre=fm(x)=fm−1(x)+T(x,θm)
-
损失函数Loss采用平方误差损失函数
- 使用CART回归树作为弱分类器,那么每次选取的特征及特征值,都会使平方误差损失函数达到最低
- 但弱分类器是不需要完全CART回归树一次性就把所有特征及特征值都遍历训练完成的,只需要挑选平方损失函数最低的那个特征及特征值
弱分类器,只进行一个树杈的划分 - 弱分类器内部的平方损失函数,是取二分树杈的左右两个数据集的平方损失之和最小
L o s s t r e e = ∑ ( y i l e f t − y ˉ l e f t ) 2 + ∑ ( y j r i g h t − y ˉ r i g h t ) 2 Loss_{tree} = ∑(y_i^{left}-\bar{y}_{left})^2+ ∑(y_j^{right}-\bar{y}_{right})^2 Losstree=∑(yileft−yˉleft)2+∑(yjright−yˉright)2 - 强分类器的平方损失函数,是取所有样本的预测值与真实值的平方损失之和最小
L o s s = ∑ ( y i − y i p r e ) 2 Loss = ∑(y_i-y_i^{pre})^2 Loss=∑(yi−yipre)2, y i y_i yi表示真实值, y i p r e y_i^{pre} yipre表示预测值
用来选取弱分类器的特征及特征值,进而将所有样本数据划分成两个子集
每个子集的预测值,是子集的均值- 根据 y p r e = f m ( x ) = f m − 1 ( x ) + T ( x , θ m ) y_{pre}=f_m(x)=f_{m-1}(x)+T(x,θ_m) ypre=fm(x)=fm−1(x)+T(x,θm),可得
- L o s s = ∑ ( y i − f m − 1 ( x ) − T ( x , θ m ) ) 2 Loss=∑(y_i-f_{m-1}(x)-T(x,θ_m))^2 Loss=∑(yi−fm−1(x)−T(x,θm))2
- 其中 y i − f m − 1 ( x ) y_i-f_{m-1}(x) yi−fm−1(x)表示上次强分类器的预测值与实际值的差,一般叫做残差(残留的差值)
- 我们可以设为 r i = y i − f m − 1 ( x ) r_i = y_i-f_{m-1}(x) ri=yi−fm−1(x),表示残差
- 那么 要使Loss达到最小,只需要当前的弱分类器,尽可能地拟合残差即可, L o s s = ∑ ( r i − T ( x , θ m ) ) 2 Loss=∑(r_i-T(x,θ_m))^2 Loss=∑(ri−T(x,θm))2
- 那么我们无需求出当前弱分类器的参数 θ,只要计算出每次的强分类器后的残差,再新增一个弱分类器,对残差进行CART回归树的拟合即可
-
每次只对残差拟合,直到Loss函数达到某个极小的阈值、特征及特征值已完全分完了,或达到迭代次数即可
2. 程序推演
设置阈值
获取所有特征及特征值
第一轮:
- 更改CART决策树,让它只每次只选择一个特征及特征值,划分数据集
- 每次划分后,计算出当前弱分类器的预测值 T m ( x , θ ) T_m(x,θ) Tm(x,θ)——对样本的数值预测
- 计算出强分类器的预测值 f m = f m − 1 + T ( x , θ ) f_m=f_{m-1}+T(x,θ) fm=fm−1+T(x,θ)
- 再计算所有样本的残差(预测值-真实值)
- 计算强分类器的平方损失函数Loss,判断是否低于阈值,若低于阈值,停止程序
第二轮:
- 根据残差,再用CART决策树,选择一个特征及特征值,划分数据集
- 每次划分后,计算出当前弱分类器的预测值 T m ( x , θ ) T_m(x,θ) Tm(x,θ)——对样本更新后的残差预测
- 计算出强分类器的预测值 f m = f m − 1 + T ( x , θ ) f_m=f_{m-1}+T(x,θ) fm=fm−1+T(x,θ)
- 再计算所有样本残差的残差(预测值-残差值)
- 计算强分类器的平方损失函数Loss,判断是否低于阈值,若低于阈值,停止程序
第三轮同第二轮…
perfect!
二叉回归树代码
确实,预测值的还不错的感觉,但不知道会不会过拟合,还没用测试数据去试。。。大概率是会过拟合的吧。。。
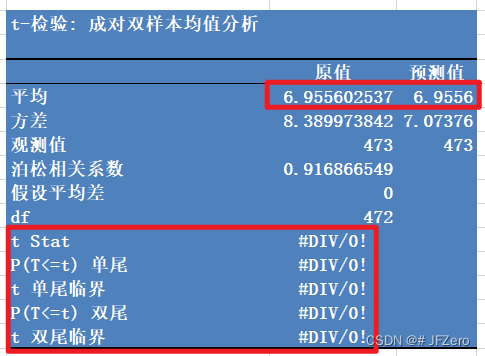
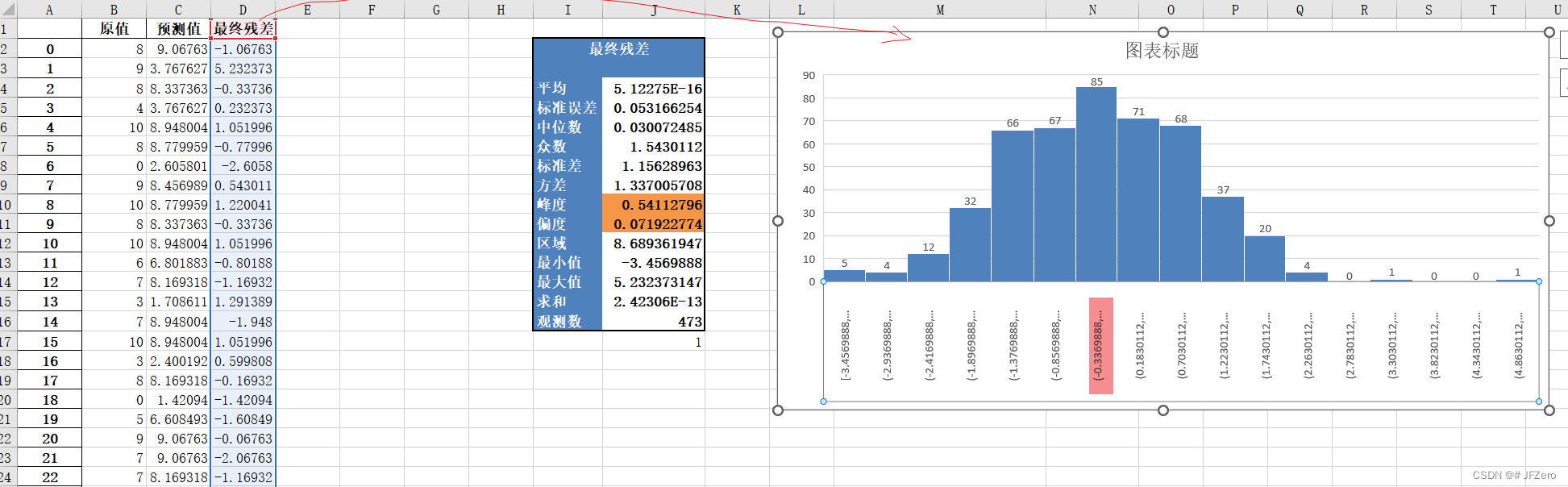
最终预测值和原值的残差,呈正态分布,且大多数聚集在0附近,本来想做个配对样本T检验的。。。但好像均值差距太小,搞不起来
import numpy as np
import pandas as pd
import warnings
warnings.filterwarnings('ignore')
pd.options.display.max_columns = None
pd.options.display.max_rows = None
# 获取所需数据:'推荐分值', '专业度','回复速度','服务态度','推荐类型'
datas = pd.read_excel('./datas4.xlsx')
important_features = ['专业度','回复速度','服务态度','推荐分值'] #datas_1 = datas[important_features]
Y = datas_1['推荐分值']
X = datas_1.drop('推荐分值',axis=1)
X_features = X.columns
Y_features = '推荐分值'# 设置阈值
# 获取所有特征及特征值
# 单次:
# 1. 更改CART决策树,让它只每次只选择一个特征及特征值,划分数据集
# 2. 每次划分后,计算出当前弱分类器的预测值$T_m(x,θ)$
# 3. 计算出强分类器的预测值$f_m=f_{m-1}+T(x,θ)$
# 4. **再计算并更新所有样本的残差(预测值-真实值)**
# 5. 计算强分类器的平方损失函数Loss,判断是否低于阈值,若低于阈值,停止程序
class CartRegTree:def __init__(self,datas,Y_feat,X_feat):self.tree_num = 0self.datas = datasself.Y_feat = Y_featself.X_feat = X_featself.all_feat_and_point = self.get_feat_and_point()self.T = {} # 用于存储所有弱分类器self.last_Loss = 0# 获取所有特征及特征值def get_feat_and_point(self):all_feat_and_point = {}for i in self.X_feat:divide_points = self.datas[i].unique()points = [j for j in divide_points]all_feat_and_point[i]=pointsreturn all_feat_and_pointdef get_tree_name(self):self.tree_num += 1return 'T'+str(self.tree_num)def get_subtree(self,datas):# 1. 选择最优的特征及特征值,划分数据集min_Loss = Nonefeat_and_point = Nonefor feat,points in self.all_feat_and_point.items():for point in points:temp_Loss = self.get_Loss_tree(datas,feat,point)if min_Loss == None or temp_Loss<min_Loss:min_Loss = temp_Lossfeat_and_point = (feat,point)left_datas = datas[datas[feat_and_point[0]]<=feat_and_point[1]]right_datas = datas[datas[feat_and_point[0]] > feat_and_point[1]]# 2.计算出当前弱分类器的预测值,存储左右子树的预测值left_Y = left_datas[self.Y_feat].mean()right_Y = right_datas[self.Y_feat].mean()T_name = self.get_tree_name()self.T[T_name]={'feat':feat_and_point[0],'point':feat_and_point[1],'left_Y':left_Y,'right_Y':right_Y}# 3. 计算并更新所有样本的残差,datas['Tm'] = np.where(datas[feat_and_point[0]]<=feat_and_point[1],left_Y,right_Y)datas[self.Y_feat] = datas[self.Y_feat]-datas['Tm']# 4. 计算残差平方和,判断是否停止Loss = round((datas[self.Y_feat]**2).sum(),2)if Loss==self.last_Loss or self.tree_num>10**3:return self.Telse:self.last_Loss = Lossself.get_subtree(datas)def get_Loss_tree(self,datas,feat,point):left_datas = datas[datas[feat]<=point]right_datas = datas[datas[feat]>point]# 求左右两边的平方损失和left_mean = left_datas[self.Y_feat].mean()right_mean = right_datas[self.Y_feat].mean()left_r = left_datas[self.Y_feat]-left_meanright_r = right_datas[self.Y_feat]-right_meanleft_loss = (left_r**2).sum()right_loss = (right_r**2).sum()Loss = left_loss+right_lossreturn Lossdef predict_one(self,data):Y_temp = 0for tree_key,tree_value in self.T.items():feat = tree_value['feat']point = tree_value['point']left_Y = tree_value['left_Y']right_Y = tree_value['right_Y']if data[feat]<=point:Y_temp += left_Yelse:Y_temp += right_Yreturn Y_tempdef predict(self,datas):Y_pre_all = datas.apply(self.predict_one,axis=1)return Y_pre_all
# 应用了pandas中的apply函数,将每行数据都进行predict运算预测
tree = CartRegTree(datas_1,Y_features,X_features)
tree.get_subtree(datas_1)
Y_hat = tree.predict(datas_1)
lenth = len(Y_hat)
result = pd.DataFrame([[i[0],i[1],i[2]] for i in zip(Y,Y_hat,Y-Y_hat)])
# result = pd.DataFrame([list(Y),list(Y_hat),list(Y-Y_hat)])
print(result)
# print(f"{Y},{Y_hat},残差:{Y-Y_hat}")writer = pd.ExcelWriter('datas_reg_result.xlsx')
# 获取所需数据
result.to_excel(writer,"result")
writer._save()
相关文章:

机器学习——boosting之提升树
提升树和adaboost基本流程是相似的 我看到提升树的时候,懵了 这…跟adaboost有啥区别??? 直到看到有个up主说了,我才稍微懂 相当于,我在adaboost里的弱分类器,换成CART决策树就好了呗࿱…...

解决Spring Boot启动错误的技术指南
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...

使用Spring Security保障你的Web应用安全
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...
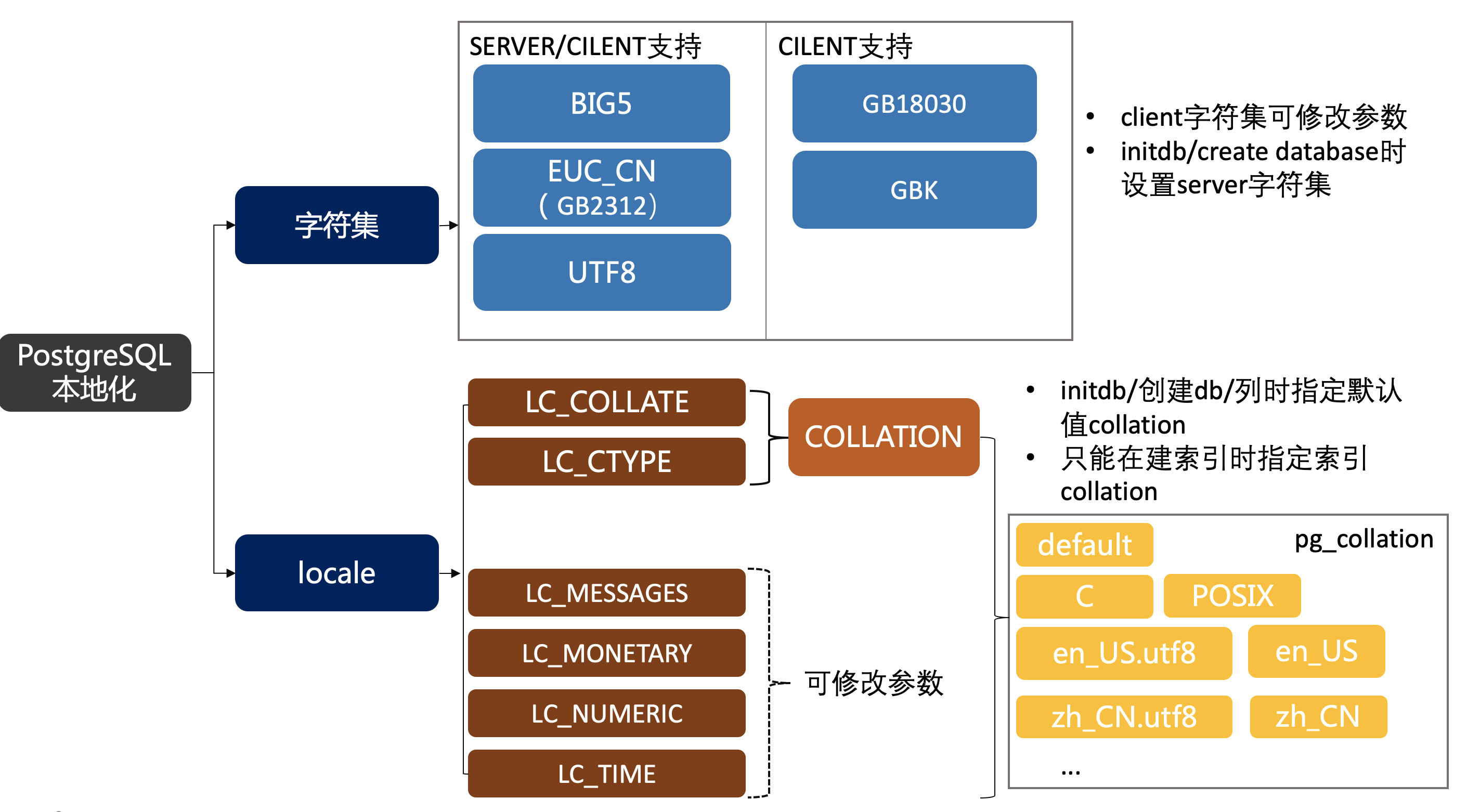
PostgreSQL本地化
本地化的概念 本地化的目的是支持不同国家、地区的语言特性、规则。比如拥有本地化支持后,可以使用支持汉语、法语、日语等等的字符集。除了字符集以外,还有字符排序规则和其他语言相关规则的支持,例如我们知道(‘a’,‘b’)该如何排序&…...
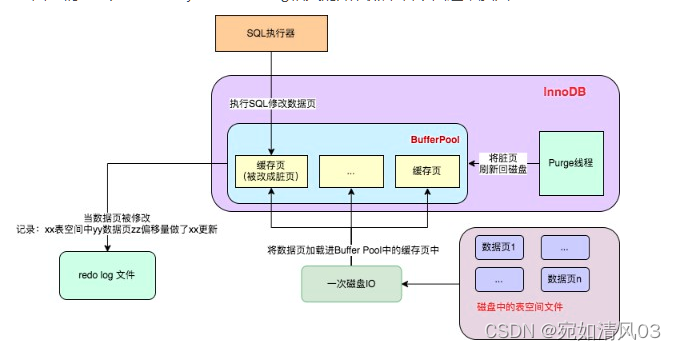
MySQL——日志
日志的作用 1.用来排错 2.用来做数据分析 3.了解程序的运行情况,是否健康--》了解MySQL的性能,运行情况 分类 mysql很多有类型的日志,按照组件划分的话,可以分为 服务层日志 和 存储引擎层日志 : - 服务层…...
)
玩转Mysql系列 - 第18篇:流程控制语句(高手进阶)
这是Mysql系列第18篇。 环境:mysql5.7.25,cmd命令中进行演示。 代码中被[]包含的表示可选,|符号分开的表示可选其一。 上一篇存储过程&自定义函数,对存储过程和自定义函数做了一个简单的介绍,但是如何能够写出复…...

LED屏幕电流驱动设计原理
LED电子显示屏作为户外最大的应用产品,是大型娱乐,体育赛事,广场大屏幕等场所不可或缺的产品,从单双色简单的文字展示到今天的高清全彩,显示屏的技术一直都在进步,全球80%的LED电子显示屏皆产自于中国。显示…...
shell知识点复习
1、shell能做什么( Shell可以做任何事(一切取决于业务需求) ) 自动化批量系统初始化程序 自动化批量软件部署程序 应用管理程序 日志分析处理程序 自动化备份恢复程序 自动化管理程序 自动化信息采集及监控程序 配合Zabbix信息采集 自动化扩容 2、获取当…...
【Sentinel Go】新手指南、流量控制、熔断降级和并发隔离控制
随着微服务的流行,服务和服务之间的稳定性变得越来越重要。Sentinel 是面向分布式、多语言异构化服务架构的流量治理组件,主要以流量为切入点,从流量路由、流量控制、流量整形、熔断降级、系统自适应过载保护、热点流量防护等多个维度来帮助开…...

iOS自定义滚动条
引言 最近一直在做数据通信相关的工作,导致了UI上的一些bug一直没有解决。这两天终于能腾出点时间大概看了一下Redmine上的bug,发现有很多bug都是与系统滚动条有关系的。所以索性就关注一下这个小小的滚动条。 为什么要自定义ScrollIndictor 原有的Scrol…...

C++知识点2:把数据写进switch case结构,和写进json结构,在使用上有什么区别
将数据存储在Switch Case结构和JSON结构中有明显的区别,它们用于不同的目的和方式。以下是它们之间的主要区别: 1、用途和结构: Switch Case结构:Switch Case是一种条件语句,通常用于根据条件执行不同的代码块。它通常…...
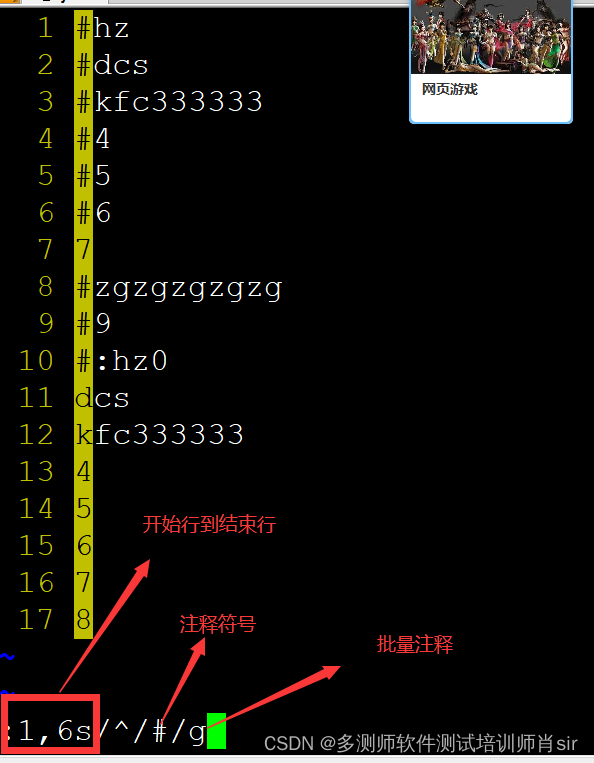
肖sir__linux详解__003(vim命令)
linux 文本编辑命令 作用:用于编辑一个文件 用法:vim 文件名称 或者vi (1)编辑一个存在的文档 例子:编辑一个file1文件 vim aa (2)编辑一个文件不存在,会先创建文件,再…...
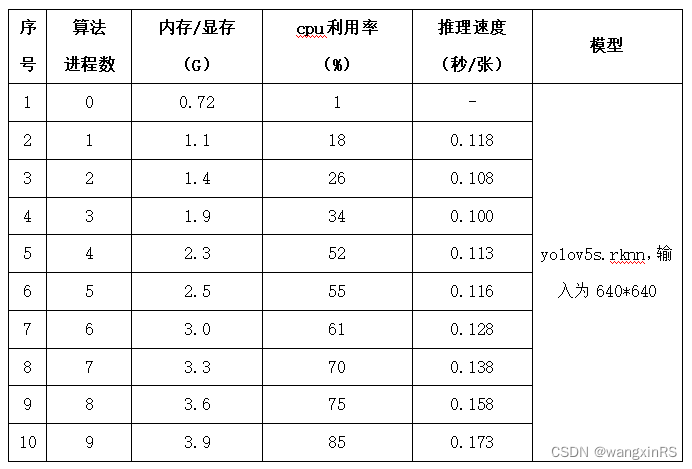
瑞芯微RK3588开发板:虚拟机yolov5模型转化、开发板上python脚本调用npu并部署 全流程
目录 0. 背景1. 模型转化1.1 基础环境1.2 创建python环境1.3 将yolov5s.pt转为yolov5s.onnx1.4 将yolov5s.onnx转为yolov5s.rknn 2. 开发板部署2.1. c版本2.1. python版本(必须是python 3.9) 3. 性能测试 0. 背景 全面国产化,用瑞芯微rk3588…...

【Redis专题】RedisCluster集群运维与核心原理剖析
目录 课程内容一、Redis集群架构模型二、Redis集群架构搭建(单机搭建)2.1 在服务器下新建各个节点的配置存放目录2.2 修改配置(以redis-8001.conf为例) 三、Java代码实战四、Redis集群原理分析4.1 槽位定位算法4.2 跳转重定位4.3 …...

我眼中的《视觉测量技术基础》
为什么会写这篇博客: 首先给大家说几点:看我的自我介绍对于学习这本书没有任何帮助,如果你是为了急切的想找一个视觉测量的解决方案那可以跳过自我介绍往下看或者换一篇博客看看,如果你是刚入门想学习计算机视觉的同学࿰…...

【Cisco Packet Tracer】管理方式,命令,接口trunk,VLAN
💐 🌸 🌷 🍀 🌹 🌻 🌺 🍁 🍃 🍂 🌿 🍄🍝 🍛 🍤 📃个人主页 :阿然成长日记 …...
深入协议栈了解TCP的三次握手、四次挥手、CLOSE-WAIT、TIME-WAIT。
TCP网络编程的代码网上很多,这里就不再赘述,简单用一个图展示一下tcp网络编程的流程: 1、深入connect、listen、accept系统调用,进一步理解TCP的三次握手 这三个函数都是系统调用,我们可以分为请求连接方和被…...

接口自动化测试系列-yml管理测试用例
项目源码 目录结构及项目介绍 整体目录结构,目录说明参考 测试用例结构类似httprunner写法,可参考demo 主要核心函数 用例读取转换json import yaml import main import os def yaml_r():curpath f{main.BASE_DIR}/quality_management_logic/ops_ne…...

开源对象存储系统minio部署配置与SpringBoot客户端整合访问
文章目录 1、MinIO安装部署1.1 下载 2、管理工具2.1、图形管理工具2.2、命令管理工具2.3、Java SDK管理工具 3、MinIO Server配置参数3.1、启动参数:3.2、环境变量3.3、Root验证参数 4、MinIO Client可用命令 官方介绍: MinIO 提供高性能、与S3 兼容的对…...
Matlab之数组字符串函数汇总
一、前言 在MATLAB中,数组字符串是指由字符组成的一维数组。字符串可以包含字母、数字、标点符号和空格等字符。MATLAB提供了一些函数和操作符来创建、访问和操作字符串数组。 二、字符串数组具体怎么使用? 1、使用单引号或双引号括起来的字符序列 例…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...
——统计抽样学习笔记(考试用))
统计学(第8版)——统计抽样学习笔记(考试用)
一、统计抽样的核心内容与问题 研究内容 从总体中科学抽取样本的方法利用样本数据推断总体特征(均值、比率、总量)控制抽样误差与非抽样误差 解决的核心问题 在成本约束下,用少量样本准确推断总体特征量化估计结果的可靠性(置…...
