树的基本概念和存储结构
一、树的基本概念
1、树的定义
树是n(n>=0)个结点的有限集。当n = 0时,称为空树。在任意一棵非空树中应满足:
1、有且仅有一个特定的称为根的结点。
2、当n>1时,其余节点可分为m(m>0)个互不相交的有限集T1,T2,…,Tm,其中每个集合本身又是一棵树,并且称为根的子树。
显然,树的定义是递归的,即在树的定义中又用到了自身,树是一种递归的数据结构。树作为一种逻辑结构,同时也是一种分层结构,具有以下特点:
①没有父节点的节点称为根节点;
②每一个非根节点有且只有一个父节点;
③每个子树是不相交的;
④n个结点的树中有n-1条边。
结合图来看,可能会更好理解
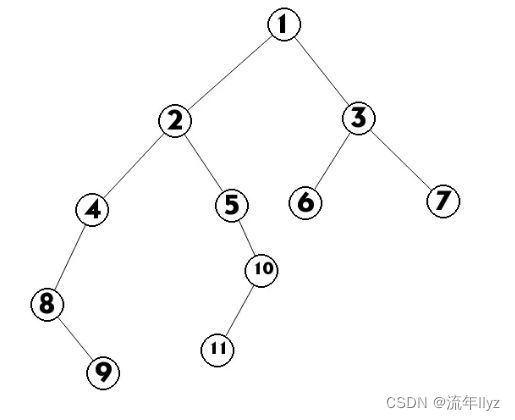
这就是一棵典型的二叉树
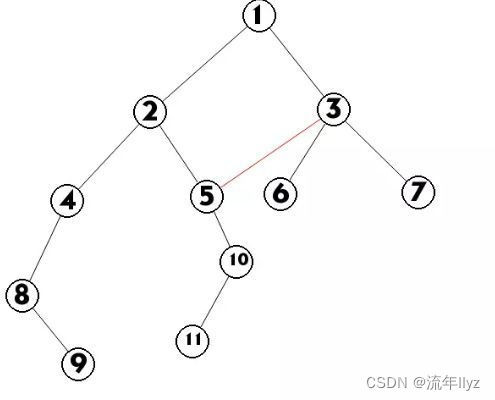
这里,2,3共有子节点5,也就是5有两个父亲,那么上图就不是树了。
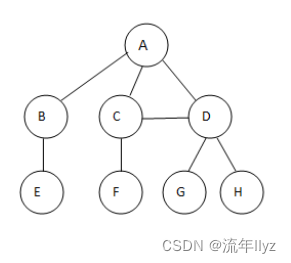
这里,CF组成的子树与DGH组成的子树相交,那么上图也不是树了。
2、基本术语
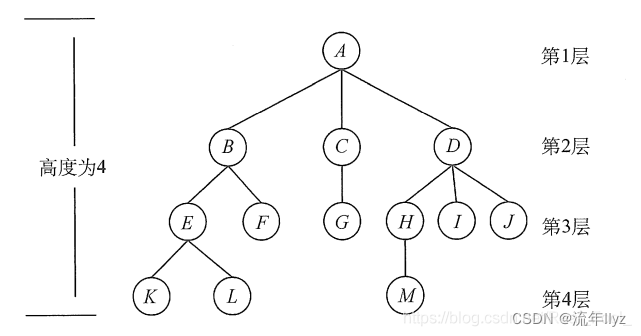
1、祖先、子孙,父亲、孩子、兄弟:
根节点A到结点K的路径上的任意结点,称为结点K的祖先。如结点B是结点K的祖先,而结点K是结点B的子孙。
路径上最接近结点K的结点E称为K的父亲,而K为结点E的孩子。根节点A是树中唯一没有父亲的结点。
有相同双亲的结点称为兄弟,如结点K和结点L有相同的双亲E,即K和L为兄弟。
2、节点的度、树的度
树中一个结点的孩子个数称为该结点的度,
树中结点的最大度数称为树的度。
如结点B的度为2,结点D的度为3,树的度为3。
3、分支结点、叶子结点
度大于0的结点称为分支结点(又称非终端结点,如BCDEH);
度为0(没有孩子结点)的结点称为叶子结点(又称终端结点,如KLFGMIJ)。
4、结点的深度、高度、层次
结点的层次从树根开始定义,根结点为第1层,它的子结点为第2层,以此类推。
双亲在同一层的结点互为堂兄弟,图中结点G与E,F,H,I,J互为堂兄弟。
结点的深度是从根结点开始自顶向下逐层累加的。
结点的高度是从叶结点开始自底向上逐层累加的。
树的高度(或深度)是树中结点的最大层数。图中树的高度为4。
5、有序树、无序树
树中任意节点的子节点之间没有顺序关系,这种树称为无序树,也称为自由树。
树中任意节点的子节点之间有顺序关系,这种树称为有序树
6、路径、路径长度。
树中两个结点之间的路径是由这两个结点之间所经过的结点序列构成的,而路径长度是路径上所经过的边的个数。
注意:由于树中的分支是有向的,即从双亲指向孩子,所以树中的路径是从上向下的,同一双亲的两个孩子之间不存在路径。
7、森林
森林是m (m≥0)棵互不相交的树的集合。
森林的概念与树的概念十分相近,因为只要把树的根结点删去就成了森林。反之,只要给m棵独立的树加上一个结点,并把这m棵树作为该结点的子树,则森林就变成了树。
注意:上述概念无须刻意记忆, 根据实例理解即可。
二、树的存储结构
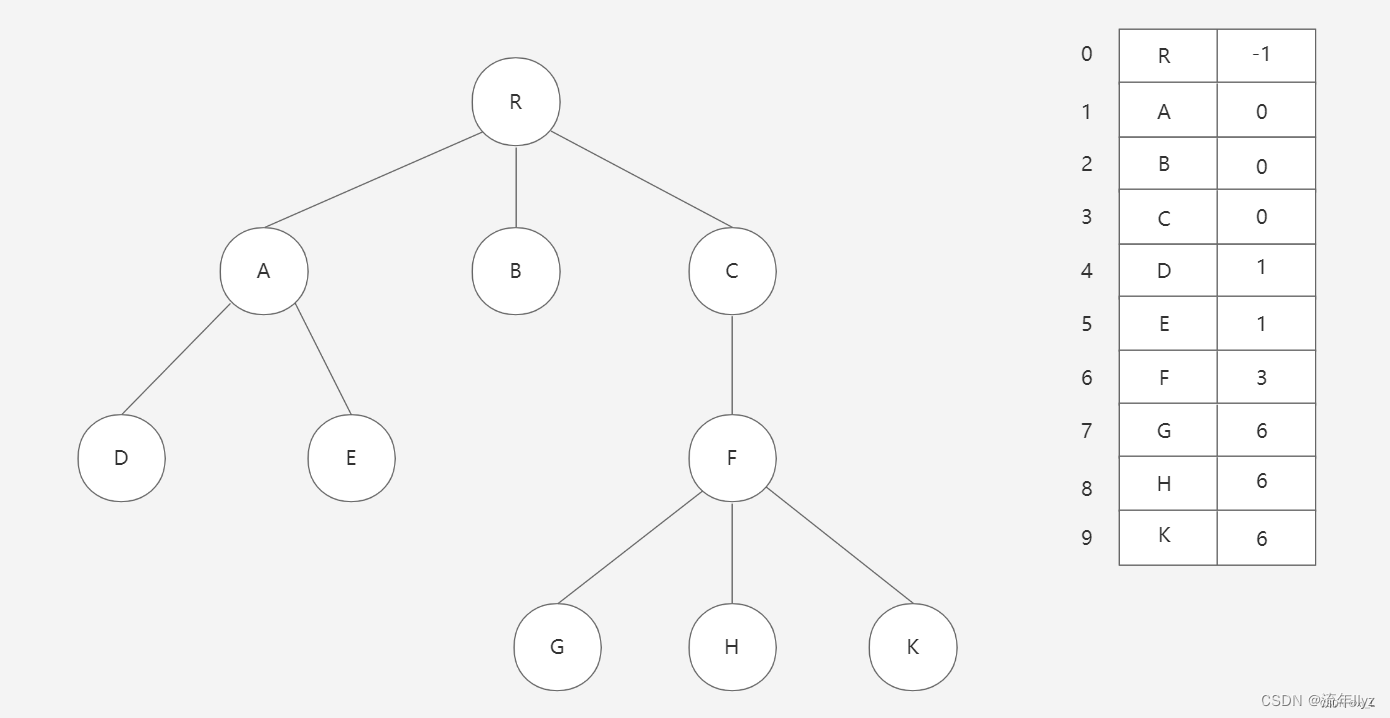
1、双亲表示法
实现:定义结构数组,存放树的结点,每个结点有两个域,分别是数据域和指针域(双亲域),数据域用于存放结点本身信息,指针域用于存放本结点的双亲结点在数组中的位置。
双亲表示的结点结构
| data(数据域) | parent(指针域) |
|---|---|
| 存储结点的数据信息 | 存储该结点的双亲所在数组中的下标 |

双亲表示法示意图:
双亲表示法结构定义:
//结点结构
struct PTNode
{ int data; //数据域int parent; //双亲域
}PTNode;//树结构struct
{PTNode nodes[100]; //结点数组int r,n; //根结点位置和结点数
}
双亲表示法的特点
- 由于根结点是没有双亲的,约定根结点的位置位置域为-1.
- 根据结点的
parent指针很容易找到它的双亲结点。所用时间复杂度为O(1),直到parent为-1时,表示找到了树结点的根。 - 缺点:如果要找到孩子结点,需要遍历整个结构才行。
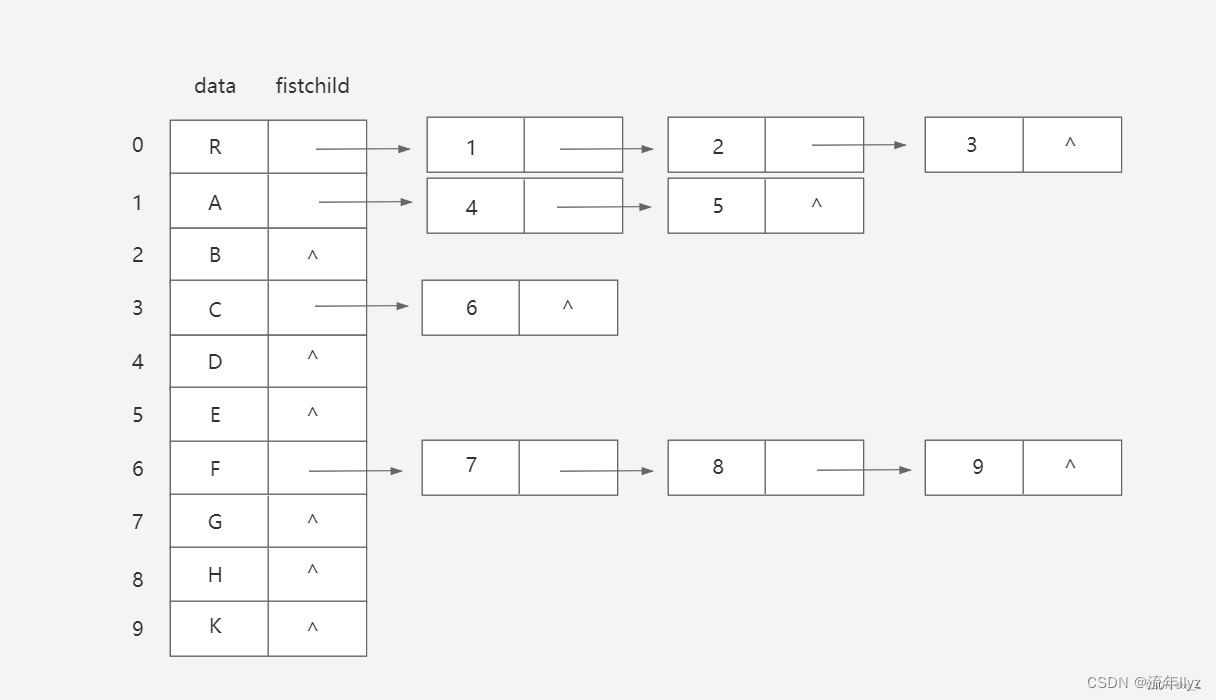
2、孩子链表法
把每个结点的孩子结点排列起来,以单链表作存储结构,则n个结点有n个孩子链表,如果是叶子结点则此单链表为空表,然后n个头指针又组成一个线性表,采用顺序存储结构,存放在一个一维数组中。
孩子表示法有两种结点结构:孩子链表的孩子结点和表头数组的表头结点
- 孩子链表的孩子结点的结点结构:
| child(数据域) | next(指针域) |
|---|---|
| 存储某个结点在表头数组中的下标 | 存储指向某结点的下一个孩子结点的指针 |

- 孩子链表的双亲结点的结点结构:
| data(数据域) | firstchild(头指针域) |
|---|---|
| 存储某个结点的数据信息 | 存储该结点的孩子链表的头指针 |

孩子链表的结构示意图:
孩子链表表示法的结构定义:
//孩子结点
typedef struct CTNode
{ int child;struct CTNode *next;
}*ChildPtr; //双亲结点
typedef struct
{ ElemType data;ChildPtr firstchild;
}CTBox;//树结构
typedef struct
{ CTBox nodes[100];int r, n; //根的位置和结点数
}CTree;
特点:找孩子容易,找双亲困难。
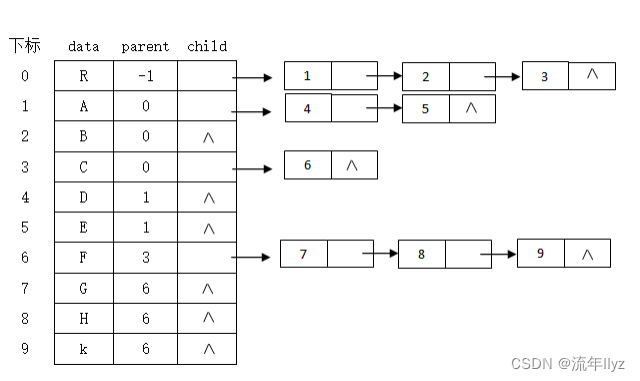
对于孩子表示法,查找某个结点的某个孩子,或者找某个结点的兄弟,只需要查找这个结点的孩子单链表即可。但是当要寻找某个结点的双亲时,就不是那么方便了。所以可以将双亲表示法和孩子表示法结合,形成双亲孩子表示法。
树的双亲孩子链表的结构示意图:
树的双亲孩子表示法结构定义:
typedef struct CTNode{ // 孩子结点int child; // 孩子结点的下标struct CTNode * next; // 指向下一结点的指针
}*ChildPtr;typedef struct { // 表头结构int data; // 存放在数中的结点数据int parent; // 存放双亲的下标ChildPtr firstchild; // 指向第一个孩子的指针
}CTBox;typedef struct { // 树结构CTBox nodes[100]; // 结点数组int r; // 根的位置int n; // 结点树
}CTree;
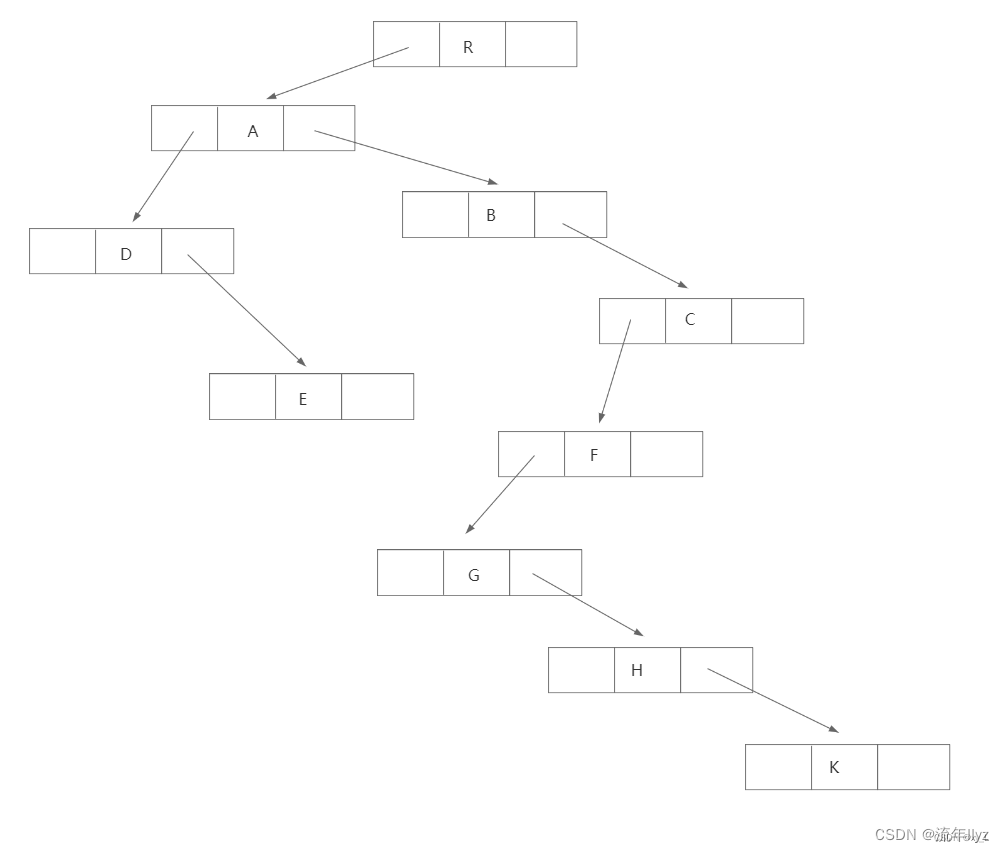
3、孩子兄弟表示法
任意一棵树,它的结点的第一个孩子如果存在就是唯一的,它的右兄弟存在也是唯一的。因此,设置两个指针,分别指向该结点的第一个孩子和此结点的右兄弟。
孩子兄弟表示法的结点结构:
| data(数据域) | firstchild(指针域) | rightsib(指针域) |
|---|---|---|
| 存储结点的数据信息 | 存储该结点的第一个孩子的存储地址 | 存储该结点的右兄弟结点的存储地址 |

孩子兄弟表示法结构示意图:
孩子兄弟结点的结构定义:
/* 树的孩子兄弟表示法结构定义*/
typedef struct CSNode{int data;struct CSNode * firstchild;struct CSNode * rightsib;}CSNode, *CSTree;相关文章:

树的基本概念和存储结构
一、树的基本概念 1、树的定义 树是n(n>0)个结点的有限集。当n 0时,称为空树。在任意一棵非空树中应满足: 1、有且仅有一个特定的称为根的结点。 2、当n>1时,其余节点可分为m(m>0)…...

深圳企业制作宣传片群体定位的重要性
相信众多企业都拍了自己公司的宣传片,尤其是在互联网高度发达的今天,宣传片可以说成为了我们企业对外宣传最主要的方式。看着企业多样式的宣传片种类,我们该如何评价一部宣传片的好坏呢?要知道宣传片的好坏是一个相对主观的问题&a…...

2309亚当arsd的11.1版本
原文 arsd11.1 Minigui 调整主题 在11.0中略有修改Minigui的主题,但它落后于11.1的计划.这是个重大更改,但这些更改很小. 新主题稍微变浅了默认组件的背景色和默认字体,这两者都主要影响Linux,因为窗口上的大多数组件一般使用本地主题. 更改状态栏 现有的状态栏类允许添加…...

spring---第七篇
系列文章目录 文章目录 系列文章目录一、什么是bean的自动装配,有哪些方式?一、什么是bean的自动装配,有哪些方式? 开启自动装配,只需要在xml配置文件中定义“autowire”属性。 <bean id="cutomer" class="com.xxx.xxx.Customer" autowire="…...
)
编程要搞明白的东西(二)
文章目录 一、简介二、面向对象编程基础2.1 面向对象编程概述2.2 类和对象2.2.1 类的定义和特点2.2.2 对象的创建和使用 2.3 封装、继承与多态的关系2.3.1 封装的概念和优势2.3.2 继承的概念和作用2.3.3 多态的概念和实现方式 三、封装3.1 封装的定义和原则3.2 封装的实现方法3…...
检索与毒害 —— 对抗人工智能供应链攻击
作者:DAVE ERICKSON 在这篇文章中,了解人工智能大语言模型的供应链漏洞,以及如何利用搜索引擎的人工智能检索技术来对抗人工智能的错误信息和故意篡改。 虽然对于人工智能研究人员来说可能是新鲜事,但供应链攻击对于网络安全世界…...

Linux 禁止用户或 IP通过 SSH 登录
Linux 禁止用户或 IP通过 SSH 登录 限制用户 SSH 登录 1.只允许指定用户进行登录(白名单): 在 /etc/ssh/sshd_config 配置文件中设置 AllowUsers 选项,(配置完成需要重启 SSHD 服务)格式如下: AllowUsers aliyun test@192.168.1.1 # 允许 aliyun 和从 19…...
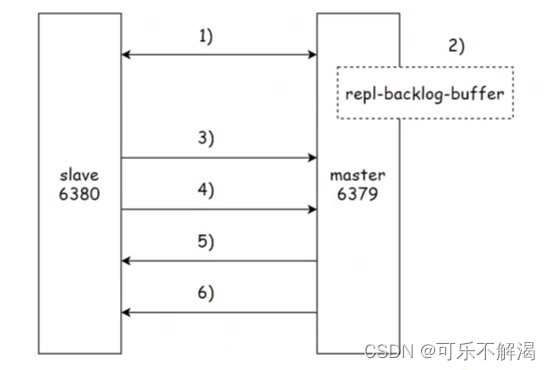
14.Redis 主从复制
Redis 主从复制 redis 主从复制配置 redis 主从复制启动 redis 主从复制断开 redis 主从复制主从复制构特点主从复制的拓扑结构一主一从⼀主多从树状主从 主从复制原理数据同步psync 运行流程全量复制流程部分复制流程实时复制 关于从节点何时晋升成主节点总结 redis 主从复制 …...

常见的图像格式介绍:RAW、RGB、YUV
常见的图像格式有RAW、RGB、YUV这三大类 1. RAW raw图像指的是sensor输出的原始数据,常见的有8位、10位、12位之分,分别表示一个像素点所占的字节数为8bit、10bit、12bit。 raw数据常见的有四种Bayer模式:GRBG、RGGB、BGGR(下图…...
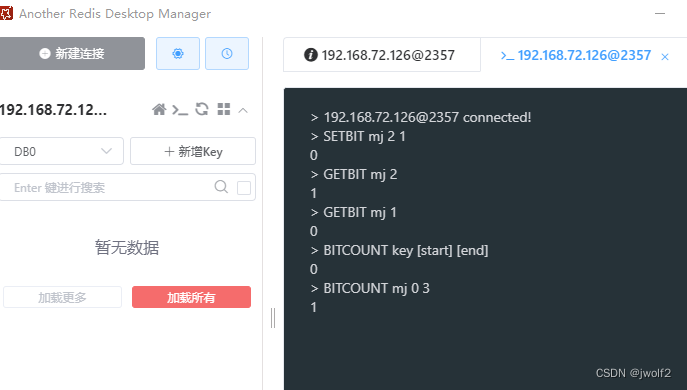
极简极速-Bitset (bitmap)实现考勤打卡场景
文章目录 1. redis命令行操作bitmap2. RedisTemplate操作bitmap3. Java中的Bitset 1. redis命令行操作bitmap 2. RedisTemplate操作bitmap bitmap的常见业务场景主要有日活统计(类似的月考勤)、点赞、BloomFilter等,以用户mj考勤统计为例&am…...
word如何插入图片?3种常用的方法
word作为一款常用的办公软件,不仅可以处理文本内容,还能够轻松地插入图片以丰富文档内容。插入图片可以使文档更具吸引力、可读性和信息传达能力。本文将为您介绍word如何插入图片的3种方法,帮助您在文档中灵活、高效地添加图像元素。 word插…...

Python/C API - 模組,型別,Tuple,例外和引用計數
Python/C API - 模組,型別,Tuple,例外和引用計數 前言Python/C API - Common Object StructuresPyObjectPyMethodDefPyGetSetDef Python/C API - Module ObjectsPyModuleDefPyModule_CreatePyModule_AddObjectPyModule_AddObjectRef Initiali…...

人工智能轨道交通行业周刊-第59期(2023.9.4-9.10)
本期关键词:无锡智慧地铁、无人车站、钢轨打磨、混元大模型、开源大模型 1 整理涉及公众号名单 1.1 行业类 RT轨道交通人民铁道世界轨道交通资讯网铁路信号技术交流北京铁路轨道交通网上榜铁路视点ITS World轨道交通联盟VSTR铁路与城市轨道交通RailMetro轨道世界…...

ASP.NET Core 中的 MVC架构
MVC 架构 MVC架构把 App 按照逻辑分成三层: Controllers,接收 http request,配合 model,通过http response 返回 view,尽量不做别的事Models, 负责业务逻辑,App 的状态,以及数据处理Views&…...
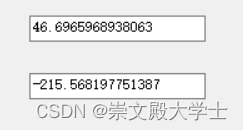
C# PSO 粒子群优化算法 遗传算法 随机算法 求解复杂方程的最大、最小值
复杂方程可以自己定义,以下是看别人的题目,然后自己来做 以下是计算结果 private void GetMinResult(out double resultX1, out double min){double x1, result;Random random1 new Random(DateTime.Now.Millisecond* DateTime.Now.Second);min 99999…...
网络协议从入门到底层原理学习(三)—— 路由
网络协议从入门到底层原理学习(三)—— 路由 1、简介 路由(routing)是指分组从源到目的地时,决定端到端路径的网络范围的进程 在不同网段之间转发数据,需要有路由器的支持 默认情况下,路由器…...

2023/9/6 -- C++/QT
一、输出流对象cout 1> 该对象是来自于ostream的类对象,功能上类似于printf函数 2> 该类对象本质上调用成员函数插入运算符重载函数 3> 输出数据时,无需使用格式控制符:%d、%c、%s。。。,直接输出即可 4> 换行使用…...

python爬虫,多线程与生产者消费者模式
使用队列完成生产者消费者模式使用类创建多线程提高爬虫速度 https://sc.chinaz.com/tupian/index.html https://sc.chinaz.com/tupian/index_2.html https://sc.chinaz.com/tupian/index_3.html from threading import Thread from queue import Queue import requests from b…...

WordPress 提示“此站点遇到了致命错误”的解决方法
WordPress 提示“此站点遇到了致命错误”的解决方法 WordPress 网站博客提示“此站点遇到了致命错误。”如何解决?今天老唐不幸遇到了这个问题,搜了一下解决方法,发现致命错误原因有很多,所以需要先打开 WordPress 的 WP_DEBUG 功…...

Vue3,Typescript中引用组件路径无法找到模块报错
是这么个事,我在vue3新创建的项目里,写了个组件叫headerIndex.vue,放到app.vue中import就会报错 路径肯定没写错,找到了解决方法,但是也没想明白为什么 解决方法如下 在vite-env.d.ts文件中加入 declare module &qu…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...
