python28种极坐标绘图函数总结
文章目录
- 基础图
- 误差线
- 等高线polar
- 场图polar
- 统计图
- 非结构坐标图
📊python35种绘图函数总结,3D、统计、流场,实用性拉满
matplotlib中的画图函数,大部分情况下只要声明坐标映射是polar,就都可以画出对应的极坐标图。但极坐标和直角坐标的坐标区间不同,所以有些数据和函数关系适合在直角坐标系中展示,而有些则适合在及坐标中展示。
基础图
| 函数 | 坐标参数 | 图形类别 | |
|---|---|---|---|
| plot | x,y | 曲线图 | |
| stackplot | x,y | 散点图 | |
| stem | x,y | 茎叶图 | |
| scatter | x,y | 散点图 | |
| polar | x,y | 极坐标图 | |
| step | x,y | 步阶图 | |
| bar | x,y | 条形图 | |
| barh | x,y | 横向条形图 |

bar和barh的对偶关系稍微有些抽象,可以理解为前者是以角度方向为x轴;而barh则是以半径方向为x轴。
代码如下
import matplotlib.pyplot as plt
import numpy as npx = np.arange(20)/2
y = xfDct = {"plot" : plt.plot, "stackplot": plt.stackplot,"stem" : plt.stem, "scatter" : plt.scatter, "polar": plt.polar, "step" : plt.step, "bar" : plt.bar, "barh" : plt.barh, }fig = plt.figure(figsize=(14,6))
for i,key in enumerate(fDct, 1):ax = fig.add_subplot(2,4,i, projection="polar")fDct[key](x, y)plt.title(key)plt.tight_layout()
plt.show()
误差线
| 函数 | 坐标 | 图形类别 |
|---|---|---|
| errorbar | x,y,xerr,yerr | 误差线 |
| fill_between | x,y1,y2 | 纵向区间图 |
| fill_betweenx | y, x1, x2 | 横向区间图 |

代码如下
x = np.arange(20)/2
y = x
y1, y2 = 0.9*y, 1.1*y
x1, x2 = 0.9*x, 1.1*x
xerr = np.abs([x1, x2])/10
yerr = np.abs([y1, y2])/10fig = plt.figure(figsize=(12,4))ax = fig.add_subplot(141, projection='polar')
ax.errorbar(x, y, yerr=yerr)
plt.title("errorbar with yerr")ax = fig.add_subplot(142, projection='polar')
ax.errorbar(x, y, xerr=xerr)
plt.title("errorbar with xerr")ax = fig.add_subplot(143, projection='polar')
ax.fill_between(x, y1, y2)
plt.title("fill_between")ax = fig.add_subplot(144, projection='polar')
ax.fill_betweenx(y, x1, x2)
plt.title("fill_betweenx")plt.tight_layout()
plt.show()
等高线polar
| 绘图函数 | 坐标 | 说明 |
|---|---|---|
| contour | [x,y,]z | 等高线 |
| contourf | [x,y,]z | 填充等高线 |
| pcolormesh | [x,y,]z | 伪彩图 |
由于imshow默认其绘图坐标是标准的1x1网格,而在极坐标种,这种网格的尺寸会随着r的增大而增大,从而变得极其不实用,所以下面对极坐标图的演示,就不包含imshow了。

代码如下
X, Y = np.indices([100,100])
X = X/100*np.pi*2
Y = Y/25 - 2
Z = (1 - np.sin(X) + np.cos(X)**5 + Y**3) * np.exp(-Y**2)fDct = {"contour": plt.contour, "contourf":plt.contourf, "pcolormesh" : plt.pcolormesh}fig = plt.figure(figsize=(9,3))
for i,key in enumerate(fDct, 1):ax = fig.add_subplot(1,3,i, projection='polar')fDct[key](X,Y,Z)plt.title(key)plt.tight_layout()
plt.show()
场图polar
| 绘图函数 | 坐标 | 说明 |
|---|---|---|
| quiver | x,y,u,v | 向量场图 |
| streamplot | x,y,u,v | 流场图 |
| barbs | x,y,u,v | 风场图 |

代码如下
Y, X = np.indices([10,10])
X = X/10*np.pi*2.5
Y = Y#Y, X = np.indices([6,6])/0.75 - 4
U = 6*np.sin(X) + Y
V = Y - 6*np.sin(X)dct = {"quiver":plt.quiver, "streamplot":plt.streamplot, "barbs" :plt.barbs}fig = plt.figure(figsize=(12,4))for i,key in enumerate(dct, 1):ax = fig.add_subplot(1,3,i,projection='polar')dct[key](X,Y,U,V)plt.title(key)plt.tight_layout()
plt.show()
统计图
| 绘图函数 | 坐标 | 说明 |
|---|---|---|
| hist | x | 数据直方图 |
| boxplot | x | 箱线图 |
| violinplot | x | 小提琴图 |
| enventplot | x | 平行线疏密图 |
| hist2d | x,y | 二维直方图 |
| hexbin | x,y | 钻石图 |
| pie | x | 饼图 |
极坐标在绘制直方图的时候,需要注意其横坐标是以 2 π 2\pi 2π为周期的,也就是说随机变量的最大值和最小值不得相差 2 π 2\pi 2π,否则会导致重叠。

由于极坐标绘图本质上是一种坐标映射,所以并不会把0和360°真正地等同起来,所以在hist2d中,整个图像并没有闭合。而最有意思的是饼图,直接给压扁了,让人很难一下子看出不同组分的比例关系。
代码如下
x = np.random.standard_normal(size=1000)dct = {"hist" : plt.hist, "violinplot" : plt.violinplot,"boxplot": plt.boxplot}fig = plt.figure(figsize=(10,6))
for i,key in enumerate(dct, 1):ax = fig.add_subplot(2,3,i, projection='polar')dct[key](x)plt.title(key)ax = fig.add_subplot(234, projection='polar')
ax.eventplot(x)
plt.title("eventplot")x = np.random.randn(5000)
y = 1.2 * x + np.random.randn(5000) / 3
ax = fig.add_subplot(235, projection='polar')
ax.hist2d(x, y, bins=[np.arange(-3,3,0.1)] * 2)
plt.title("hist2d")ax = fig.add_subplot(236, projection='polar')
ax.pie([1,2,3,4,5])
plt.title("pie")plt.tight_layout()
plt.show()
非结构坐标图
| 绘图函数 | 坐标 | 说明 |
|---|---|---|
| tricontour | x,y,z | 非结构等高线 |
| tricontourf | x,y,z | 非结构化填充等高线 |
| tricolor | x,y,z | 非结构化伪彩图 |
| triplot | x,y | 三角连线图 |

代码如下
x = np.random.uniform(0, np.pi*2, 256)
y = np.random.uniform(-2, 2, 256)
z = (1 - np.sin(x) + np.cos(x)**5 + y**3) * np.exp(-y**2)levels = np.linspace(z.min(), z.max(), 7)fig = plt.figure(figsize=(12,4))ax = fig.add_subplot(141, projection='polar')
ax.plot(x, y, 'o', markersize=1, color='lightgrey', alpha=0.5)
ax.tricontour(x, y, z, levels=levels)
plt.title("tricontour")ax = fig.add_subplot(142, projection='polar')
ax.plot(x, y, 'o', markersize=1, color='lightgrey', alpha=0.5)
ax.tricontourf(x, y, z, levels=levels)
plt.title("tricontourf")ax = fig.add_subplot(143, projection='polar')
ax.plot(x, y, 'o', markersize=1, color='lightgrey', alpha=0.5)
ax.tripcolor(x, y, z)
plt.title("tripcolor")ax = fig.add_subplot(144, projection='polar')
ax.triplot(x,y)
plt.title("triplot")plt.tight_layout()
plt.show()
相关文章:

python28种极坐标绘图函数总结
文章目录 基础图误差线等高线polar场图polar统计图非结构坐标图 📊python35种绘图函数总结,3D、统计、流场,实用性拉满 matplotlib中的画图函数,大部分情况下只要声明坐标映射是polar,就都可以画出对应的极坐标图。但…...

C#编程基础(万字详解,这一篇就够了)
C#及其开发环境简介 C#概述 C#的编程功能 C#与.Net的关系 .Net C# C#的集成开发环境 Windows上编写C#程序 Linux/Mac OS上编写C#程序 运行第一个HelloWorld程序 C#基本语法 程序实例 C#基本语法 using关键字 class关键字 注释 成员变量 成员函数 实例化一个类…...

SpringBoot中自定义注解
目录 SpringBoot中自定义注解 关于注解的解释 元注解 Documented Target Retention Inherited Native 自定义注解 自定义注解与SpringBoot全局异常处理完成参数校验 约束验证器 自定义全局异常处理器 自定义注解完成数据脱敏 定义脱敏策略枚举 自定义注解 实行脱…...

《TCP/IP网络编程》阅读笔记--地址族和数据序列
目录 1--IP地址和端口号 2--地址信息的表示 3--网络字节序与地址变换 4--网络地址的初始化与分配 5--Windows部分代码案例 1--IP地址和端口号 IP 地址分为两类: ① IPv4 表示 4 字节地址族; ② IPv6 表示 16 字节地址族; IPv4 标准的 4 …...

【C++】可变参数模板
2023年9月9日,周六下午 这个还是挺难学的,我学了好几天... 在这里我会举大量的示例程序,这样可以有一个更好的理解, 不定期更新。 目录 推荐文章: 示例程序一:拼接字符串 示例程序二:求整…...
WPF Flyout风格动画消息弹出消息提示框
WPF Flyout风格动画消息弹出消息提示框 效果如图: XAML: <Window x:Class"你的名称控件.FlyoutNotication"xmlns"http://schemas.microsoft.com/winfx/2006/xaml/presentation"xmlns:x"http://schemas.microsoft.com/winfx/2006/xam…...

Spring Boot 集成 Redis
Spring-data-redis 在 Spring 中整合 Redis jedis : 采用的直连,多个线程操作的话,是不安全的,如果想要避免不安全的,使用 jedis pool 连接池 lettuce : 采用netty,实例可以再多个线程中进行共享,不存在…...

Java线程之间通信方式
目录 1 线程之间的通信方式主要有以下几种2 共享变量3 锁机制4 条件变量5 信号量6 管道 1 线程之间的通信方式主要有以下几种 在实际开发时,一个进程中往往有很多个线程,大多数线程之间往往不是绝对独立的,比如说我们需要将A和B 两个线程的执…...

【LeetCode-中等题】367. 有效的完全平方数
文章目录 题目方法一:二分查找 题目 方法一:二分查找 找 1 - num 之间的 mid, 开方是整数 就找得到 mid, 不是整数自然找不到mid class Solution { // 二分查找 ;找 1 - num 之间的mid 开方是整数 就找得到 不是…...

英语单词(二)
1.int:整形 2.char:字符型 3.scanner:接受输入,扫描器 4.integer:整数,整形 5.type:类型 6.string:字符串类型 7.double:双精度浮点型...

Django 用相对路径方式引用自定义模块 或 文件
Django的文件夹结构 projectName/websiteName/appName manage.py 所在路径为:D:/projectA/website1/manage.py views.py 所在路径为:D:/projectA/website1/app1/views.py D:/projectA/website1/app1/module1.py 如果要引用自定义模块,引用…...
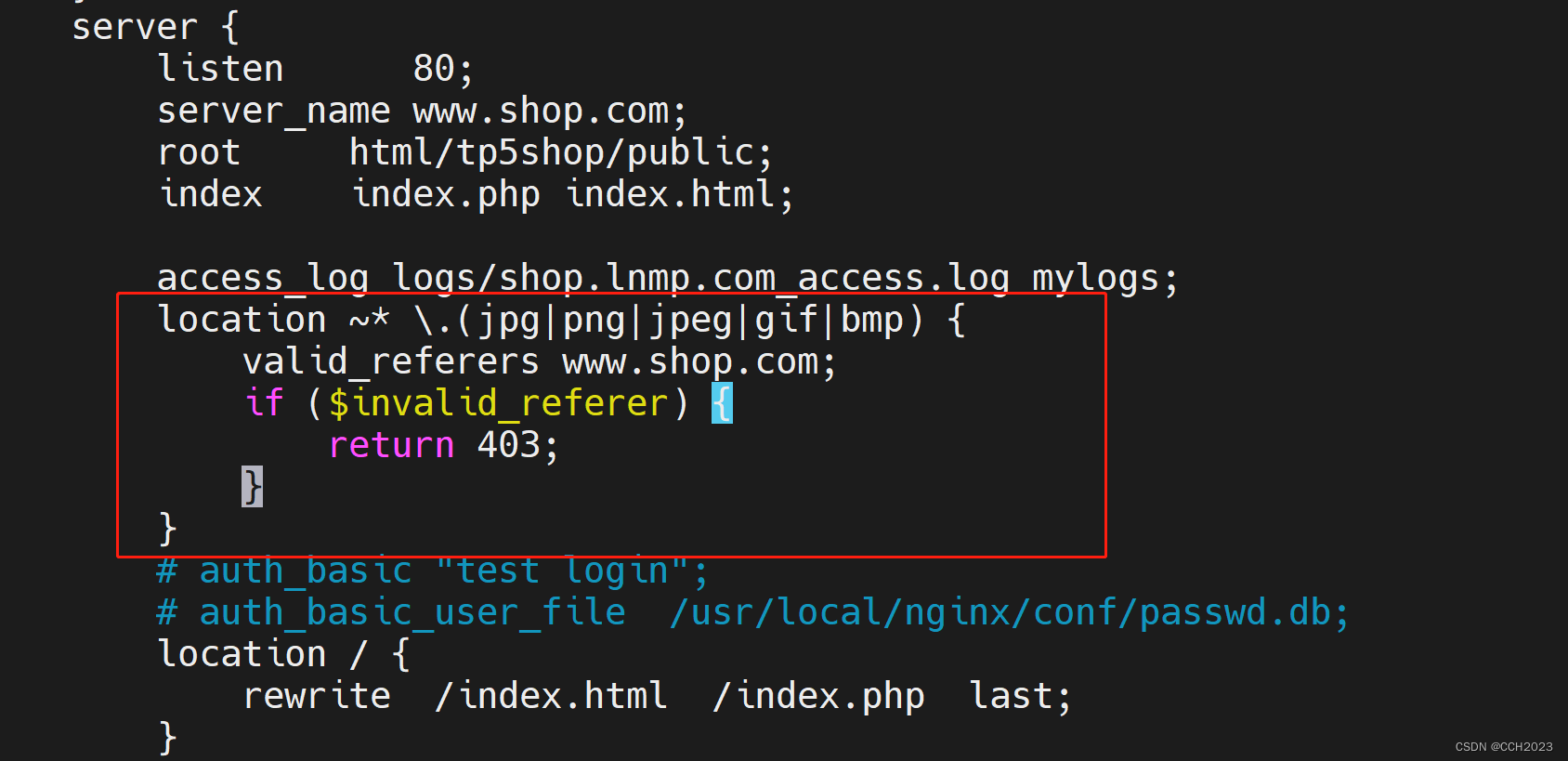
企业架构LNMP学习笔记22
防盗链原理和实现。 域名A的资源文件,经常被域名B直接调用访问。 而用户经常访问域名B,看到的资源(图片等)以为是域名B的,实际则是域名A的。 但是域名A没有获得任何收益,却要给域名B来源的访问消耗服务器…...

uniapp和小程序设置tabBar和显示与隐藏tabBar
(1)设置tabBar: uni.setTabberItem({ }); wx.setTabberItem({ }); 属性值: indexnumber是tabBar 的哪一项,从左边算起,索引从0开始textstring否tab 上按钮文字iconPathstring否图片路径selectedIc…...

物联网、无线通讯
LAN:局域网 Local Area Network WAN:广域网 Wide Area Network WLAN:无线局域网 Wireless LAN LPWAN:低功耗广域网 Low Power Wide Area Network技术特点无线通信技术应用场景高功耗、高速率的远距离传输3G、4G蜂窝这类传输技术适…...
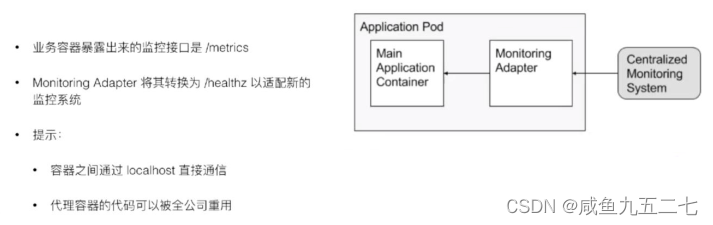
Pod和容器设计模式
为什么需要Pod 一些应用的实现是需要多个进程配合完成的,由于容器实际上是一个“单进程”模型,如果在容器里启动多个进程会存在进程管理的难题。在Kubernetes里面,实际上会被定义为一个拥有四个容器的Pod。 Pod相当于进程组 Kubernetes 是…...

docker系列(3) - 常用软件安装
文章目录 3. docker安装常用软件3.1 安装nginx3.2 安装redis3.3 安装mysql3.4 部署springboot程序3.4.1 编写dockerfile3.4.2 构建镜像3.4.3 启动镜像 3. docker安装常用软件 3.1 安装nginx docker pull nginx#挂载启动 docker run -it -d \ --namenginx \ --networkpub_netw…...

Apache Hive之数据查询
文章目录 版权声明数据查询环境准备基本查询准备数据select基础查询分组、聚合JOINRLIKE正则匹配UNION联合Sampling采用Virtual Columns虚拟列 版权声明 本博客的内容基于我个人学习黑马程序员课程的学习笔记整理而成。我特此声明,所有版权属于黑马程序员或相关权利…...

OpenCV---视频操作
用摄像头捕获视频 import cv2 as cv import numpy cap cv.VideoCapture(0) while(cap.isOpened()):ret, frame cap.read() # read() 它返回两个值,第一个是布尔值,表示是否成功读取到一帧,第二个是帧本身。cv.imshow(Video, frame)if c…...

《TCP/IP网络编程》阅读笔记--进程间通信
目录 1--进程间通信 2--pipe()函数 3--代码实例 3-1--pipe1.c 3-2--pipe2.c 3-3--pipe3.c 3-4--保存信息的回声服务器端 1--进程间通信 为了实现进程间通信,使得两个不同的进程间可以交换数据,操作系统必须提供两个进程可以同时访问的内存空间&am…...

mysql中show status参数介绍
Uptime_since_flush_status, 2159061:自上次刷新状态以来的服务器运行时间(以秒为单位)。Uptime, 2159061:服务器的总运行时间(以秒为单位)。Threads_running, 2:当前正在运行的客户端线程数。T…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

tauri项目,如何在rust端读取电脑环境变量
如果想在前端通过调用来获取环境变量的值,可以通过标准的依赖: std::env::var(name).ok() 想在前端通过调用来获取,可以写一个command函数: #[tauri::command] pub fn get_env_var(name: String) -> Result<String, Stri…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...
