Flutter yuv 转 rgb
1、引用yuv_converter库
yuv_converter: ^0.0.12、导入头文件:
import 'package:yuv_converter/yuv_converter.dart';
3、yuv转rgb
YuvConverter.yuv420NV21ToRgba8888(yuvRawData, 512, 512)根据yuv格式选择不同的api。
举个例子:
void initState() {super.initState() ;loadAssetAsUint8List("assets/yuv/1_uyvy.yuv").then((yuvRawData){rgbga1 = YuvConverter.yuv422uyvyToRgba8888(yuvRawData, 512, 512) ;setState(() {});}) ;loadAssetAsUint8List("assets/yuv/1_nv21.yuv").then((yuvRawData){rgbga2 = YuvConverter.yuv420NV21ToRgba8888(yuvRawData, 512, 512) ;setState(() {});}) ;}Future<Uint8List> loadAssetAsUint8List(String assetPath) async {// 使用rootBundle加载assets中的文件final ByteData data = await rootBundle.load(assetPath);// 将ByteData转换为Uint8Listfinal Uint8List uint8List = data.buffer.asUint8List();return uint8List;}github:
https://github.com/menshen/flutter_yuv_converter
相关文章:

Flutter yuv 转 rgb
1、引用yuv_converter库 yuv_converter: ^0.0.1 2、导入头文件: import package:yuv_converter/yuv_converter.dart;3、yuv转rgb YuvConverter.yuv420NV21ToRgba8888(yuvRawData, 512, 512) 根据yuv格式选择不同的api。 举个例子: void initState() …...

MySQL——子查询
2023.9.8 相关学习笔记: #子查询 /* 含义: 出现在其他语句中的select语句,称为子查询或内查询 外部的查询语句,称为主查询或外查询分类: 按子查询出现的位置:select后面:仅仅支持标量子查询fro…...
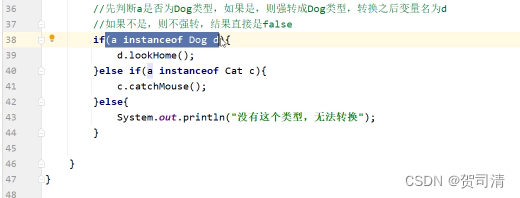
Java学习笔记---多态
面向对象三大特征之一(继承,封装,多态) 多态的应用场景:根据传递对象的不同,调用不同的show方法 一、多态的定义 同类型的对象,表现出的不同形态(对象的多种形态) 二…...

2023-09-10 LeetCode每日一题(课程表 II)
2023-09-10每日一题 一、题目编号 210. 课程表 II二、题目链接 点击跳转到题目位置 三、题目描述 现在你总共有 numCourses 门课需要选,记为 0 到 numCourses - 1。给你一个数组 prerequisites ,其中 prerequisites[i] [ai, bi] ,表示在…...

合并区间【贪心算法】
合并区间 以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。 class Solution {public int[][] merge(int[…...
2023,软件测试人的未来在哪里?
2023年,IT行业出现空前的萧条,首先是年初一开始各大厂像着了魔似的不约而同的纷纷裁员、降薪、奖金包缩水,随之而来的是需求萎缩,HC减少或封锁等等。 而有幸未被列入裁员名单的在职人员,庆幸之余也心有余悸࿰…...
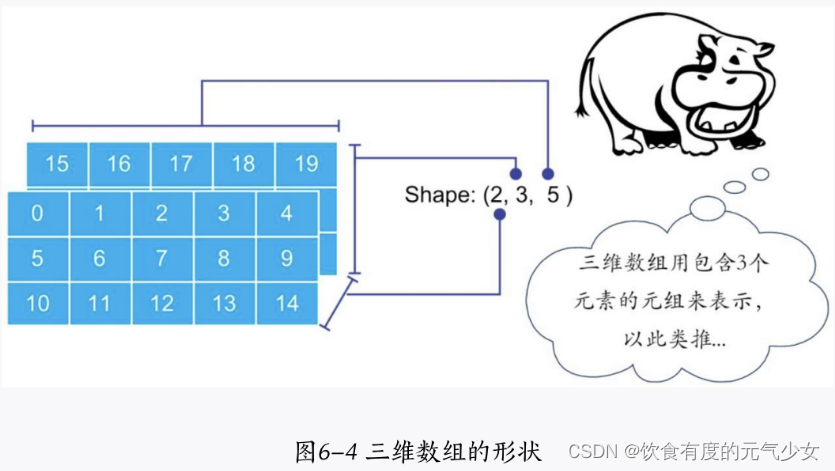
Python中的Numpy向量计算(R与Python系列第三篇)
目录 一、什么是Numpy? 二、如何导入NumPy? 三、生成NumPy数组 3.1利用序列生成 3.2使用特定函数生成NumPy数组 (1)使用np.arange() (2)使用np.linspace() 四、NumPy数组的其他常用函数 (1)np.z…...
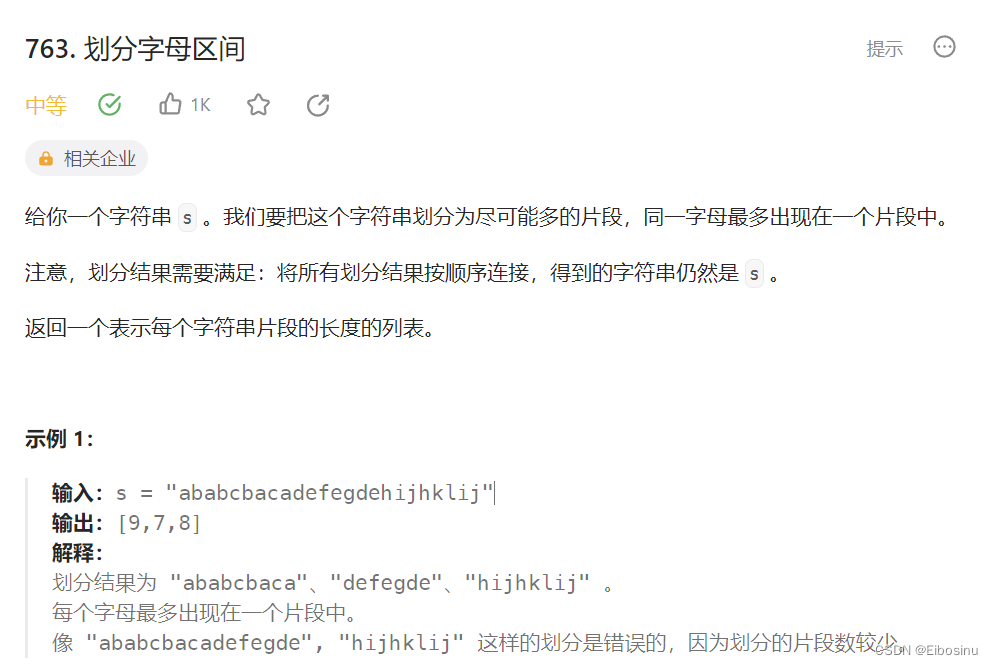
LeetCode刷题笔记【27】:贪心算法专题-5(无重叠区间、划分字母区间、合并区间)
文章目录 前置知识435. 无重叠区间题目描述参考<452. 用最少数量的箭引爆气球>, 间接求解直接求"重叠区间数量" 763.划分字母区间题目描述贪心 - 建立"最后一个当前字母"数组优化marker创建的过程 56. 合并区间题目描述解题思路代码① 如果有重合就合…...

nvidia-smi 命令详解
nvidia-smi 命令详解 1. nvidia-smi 面板解析2. 显存与GPU的区别 Reference: nvidia-smi命令详解 相关文章: nvidia-smi nvcc -V 及 CUDA、cuDNN 安装 nvidia-smi(NVIDIA System Management Interface) 是一种命令行实用程序,用于监控和管理 NVIDIA G…...
函数的返回值)
fork()函数的返回值
在程序中,int pd fork() 是一个典型的 fork() 调用。fork() 函数会创建一个新的进程,然后在父进程中返回子进程的进程ID(PID),在子进程中返回0。所以 pd 的值会根据当前进程是父进程还是子进程而有所不同:…...
)
Stable Diffusion WebUI挂VPN不能跑图解决办法(Windows)
如何解决SD在打开VPN的状态不能运行的问题 在我们开VPN的时候会出现无法生成图片,也无法做其他任何事,这个时候是不是很着急呢? 别急,我这里会说明如何解决。 就像这样,运行半天生成不了图,有时还会出现…...

Android的本地数据
何为本地,即写完之后除非手动修改,否像嘎了一样在那固定死了 有些需求可能也会要求我们去写死数据,因为这需求是一成不变的,那么你通常会用什么方法写死呢? 1. 本地存储-SharedPreferences 此方法可以长时间保存于手…...

android NDK 开发包,网盘下载,不限速
记录下ndk 开发包的地址,分享给大家。 另外有Android studio的下载包, 在另一篇文章 链接:http://t.csdn.cn/JSr9x Android Studio.exe 下载 2023 最新更新,网盘下载_hsj-obj的博客-CSDN博客 主要是19-25,其他的没有…...

【每日一题Day320】LC2651计算列车到站时间 | 数学
计算列车到站时间【LC2651】](https://leetcode.cn/problems/calculate-delayed-arrival-time/) 给你一个正整数 arrivalTime 表示列车正点到站的时间(单位:小时),另给你一个正整数 delayedTime 表示列车延误的小时数。 返回列车实…...
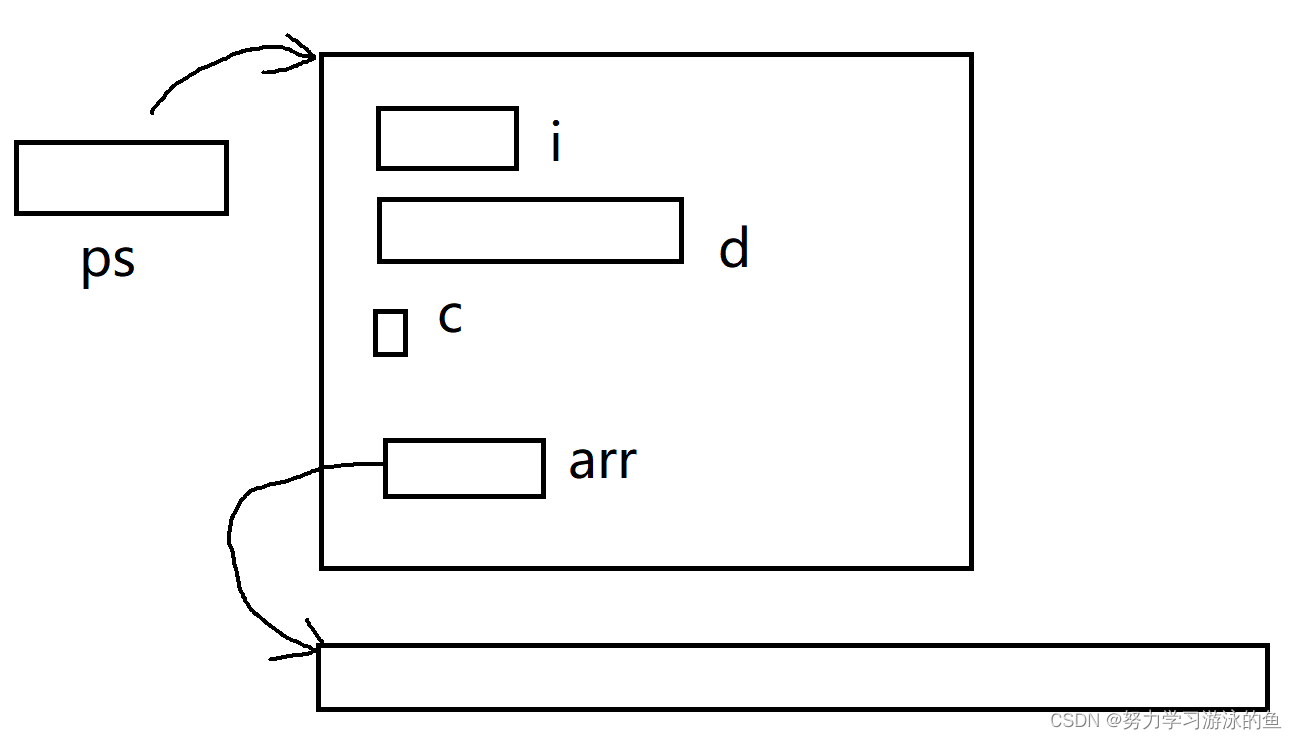
C语言柔性数组详解:让你的程序更灵活
柔性数组 一、前言二、柔性数组的用法三、柔性数组的内存分布四、柔性数组的优势五、总结 一、前言 仔细观察下面的代码,有没有看出哪里不对劲? struct S {int i;double d;char c;int arr[]; };还有另外一种写法: struct S {int i;double …...
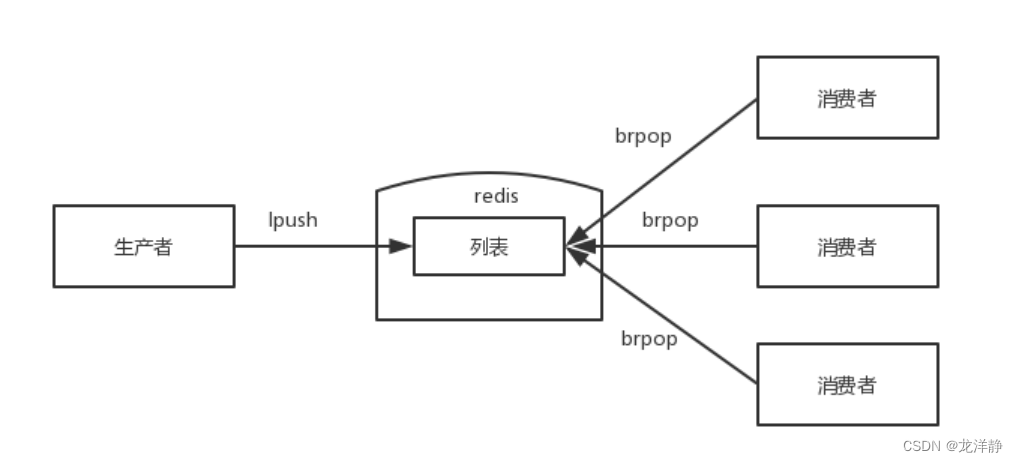
Redis-带你深入学习数据类型list
目录 1、list列表 2、list相关命令 2.1、添加相关命令:rpush、lpush、linsert 2.2、查找相关命令:lrange、lindex、llen 2.3、删除相关命令:lpop、rpop、lrem、ltrim 2.4、修改相关命令:lset 2.5、阻塞相关命令:…...

react拖拽依赖库react-dnd
注:对于表格自定义行可以拖拽和树自定义节点可以拖拽等比较适用,其余的拖拽处理可以使用dragstart,drop等js原生事件来实现 react-dnd使用方法很简单,直接上干货 第一步安装依赖并引入 import { DndProvider } from react-dnd;…...
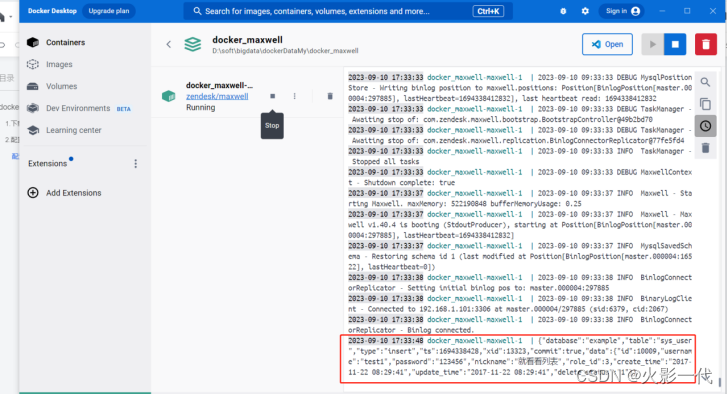
win10环境安装使用docker-maxwell
目的:maxwell可以监控mysql数据变化,并同步到kafka、mq或tcp等。 maxwell和canal区别: maxwell更轻量,canal把表结构也输出了 docker bootstrap可导出历史数据,canal不能 环境 :win10,mysql5…...
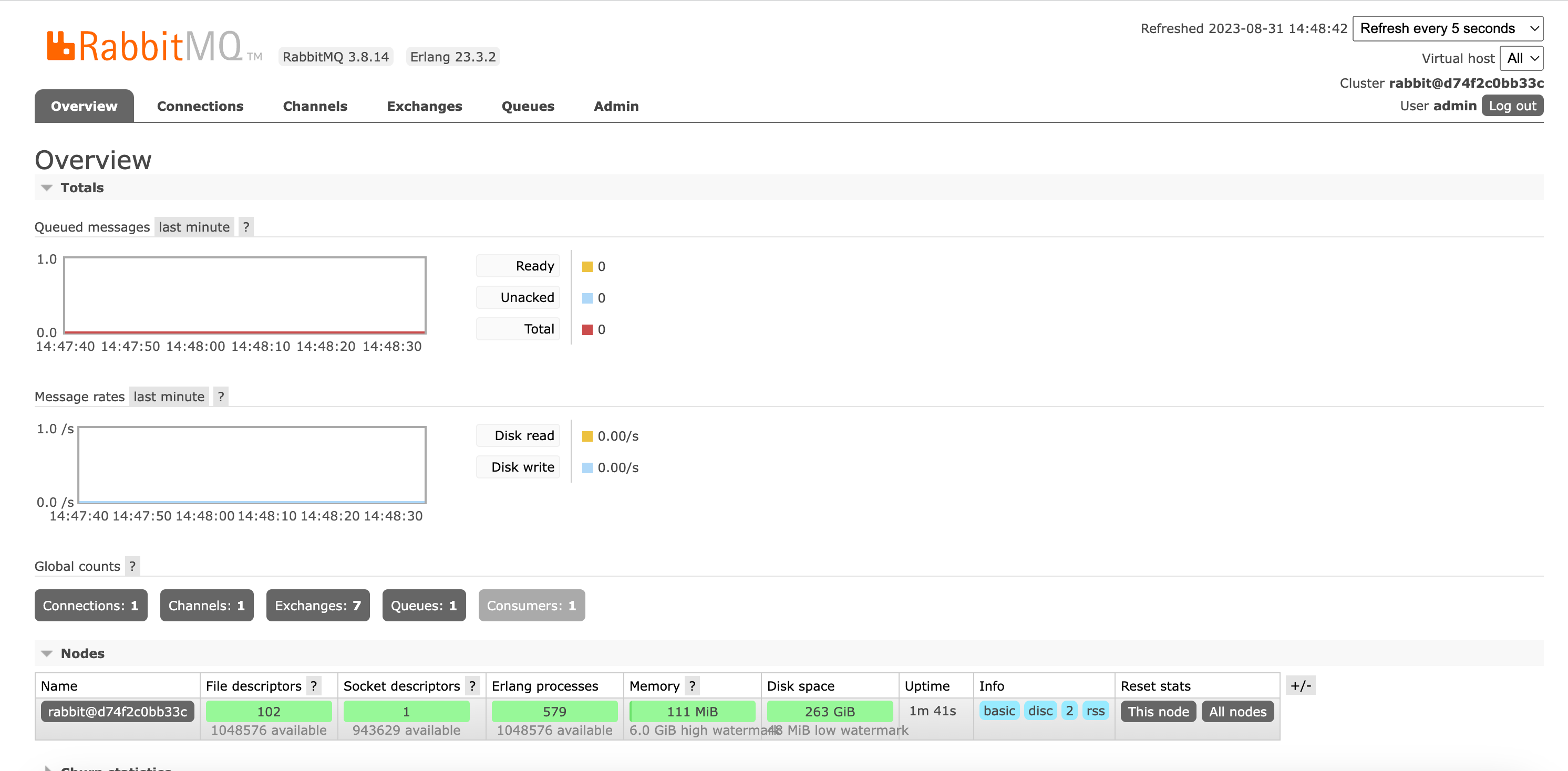
Docker部署RabbitMQ
Docker部署RabbitMQ 介绍 RabbitMQ是一个开源的消息队列系统,它被设计用于在应用程序之间传递消息。它采用了AMQP(高级消息队列协议)作为底层通信协议,这使得它能够在不同的应用程序之间进行可靠的消息传递。 那么,…...
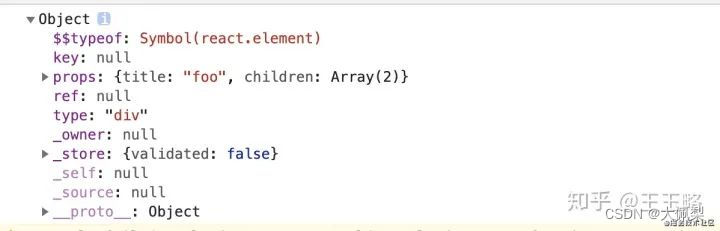
23个react常见问题
1、setState 是异步还是同步? 合成事件中是异步 钩子函数中的是异步 原生事件中是同步 setTimeout中是同步 相关链接:你真的理解setState吗?: 2、聊聊 react16.4 的生命周期 图片 相关连接:React 生命周期 我对 Reac…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...
