YOLOv5改进算法之添加CA注意力机制模块
目录
1.CA注意力机制
2.YOLOv5添加注意力机制
送书活动
1.CA注意力机制
CA(Coordinate Attention)注意力机制是一种用于加强深度学习模型对输入数据的空间结构理解的注意力机制。CA 注意力机制的核心思想是引入坐标信息,以便模型可以更好地理解不同位置之间的关系。如下图:
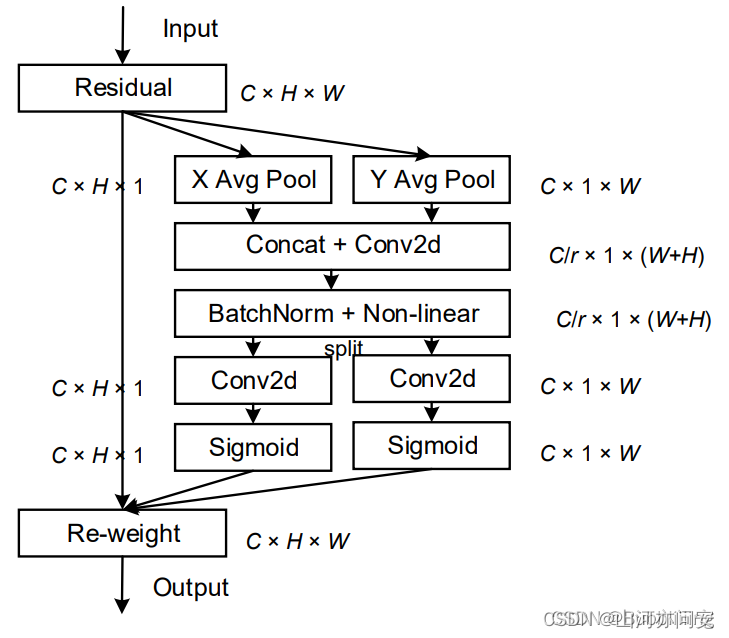
1. 输入特征: CA 注意力机制的输入通常是一个特征图,它通常是卷积神经网络(CNN)中的某一层的输出,具有以下形状:[C, H, W],其中:
C是通道数,表示特征图中的不同特征通道。H是高度,表示特征图的垂直维度。W是宽度,表示特征图的水平维度。
2. 全局平均池化: CA 注意力机制首先对输入特征图进行两次全局平均池化,一次在宽度方向上,一次在高度方向上。这两次操作分别得到两个特征映射:
- 在宽度方向上的平均池化得到特征映射
[C, H, 1]。 - 在高度方向上的平均池化得到特征映射
[C, 1, W]。
这两个特征映射分别捕捉了在宽度和高度方向上的全局特征。
3. 合并宽高特征: 将上述两个特征映射合并,通常通过简单的堆叠操作,得到一个新的特征层,形状为 [C, 1, H + W],其中 H + W 表示在宽度和高度两个方向上的维度合并在一起。
4. 卷积+标准化+激活函数: 对合并后的特征层进行卷积操作,通常是 1x1 卷积,以捕捉宽度和高度维度之间的关系。然后,通常会应用标准化(如批量标准化)和激活函数(如ReLU)来进一步处理特征,得到一个更加丰富的表示。
5. 再次分开: 分别从上述特征层中分离出宽度和高度方向的特征:
- 一个分支得到特征层
[C, 1, H]。 - 另一个分支得到特征层
[C, 1, W]。
6. 转置: 对分开的两个特征层进行转置操作,以恢复宽度和高度的维度,得到两个特征层分别为 [C, H, 1] 和 [C, 1, W]。
7. 通道调整和 Sigmoid: 对两个分开的特征层分别应用 1x1 卷积,以调整通道数,使其适应注意力计算。然后,应用 Sigmoid 激活函数,得到在宽度和高度维度上的注意力分数。这些分数用于指示不同位置的重要性。
8. 应用注意力: 将原始输入特征图与宽度和高度方向上的注意力分数相乘,得到 CA 注意力机制的输出。
2.YOLOv5添加注意力机制
在models/common.py文件中增加以下模块:
import torch
import torch.nn as nn
import torch.nn.functional as Fclass h_sigmoid(nn.Module):def __init__(self, inplace=True):super(h_sigmoid, self).__init__()self.relu = nn.ReLU6(inplace=inplace)def forward(self, x):return self.relu(x + 3) / 6class h_swish(nn.Module):def __init__(self, inplace=True):super(h_swish, self).__init__()self.sigmoid = h_sigmoid(inplace=inplace)def forward(self, x):return x * self.sigmoid(x)class CoordAtt(nn.Module):def __init__(self, inp, reduction=32):super(CoordAtt, self).__init__()self.pool_h = nn.AdaptiveAvgPool2d((None, 1))self.pool_w = nn.AdaptiveAvgPool2d((1, None))mip = max(8, inp // reduction)self.conv1 = nn.Conv2d(inp, mip, kernel_size=1, stride=1, padding=0)self.bn1 = nn.BatchNorm2d(mip)self.act = h_swish()self.conv_h = nn.Conv2d(mip, inp, kernel_size=1, stride=1, padding=0)self.conv_w = nn.Conv2d(mip, inp, kernel_size=1, stride=1, padding=0)def forward(self, x):identity = xn, c, h, w = x.size()x_h = self.pool_h(x)x_w = self.pool_w(x).permute(0, 1, 3, 2)y = torch.cat([x_h, x_w], dim=2)y = self.conv1(y)y = self.bn1(y)y = self.act(y)x_h, x_w = torch.split(y, [h, w], dim=2)x_w = x_w.permute(0, 1, 3, 2)a_h = self.conv_h(x_h).sigmoid()a_w = self.conv_w(x_w).sigmoid()out = identity * a_w * a_hreturn out在models/yolo.py文件下里的parse_model函数将类名加入进去,如下图:
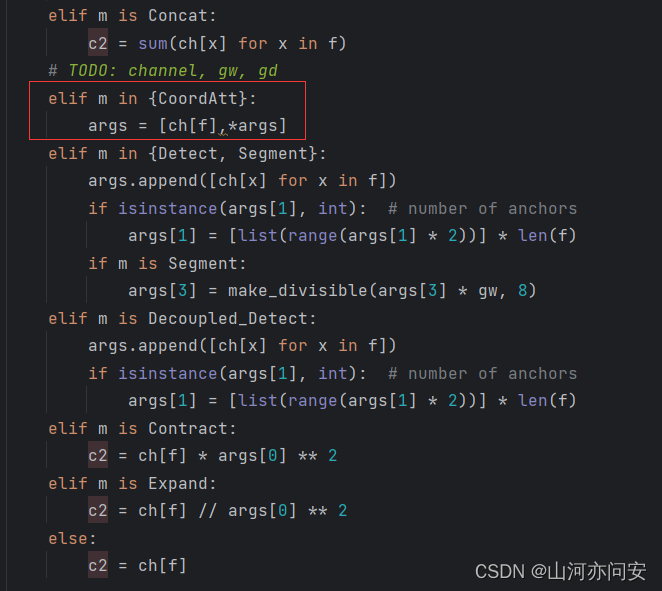
创建添加CA模块的YOLOv5的yaml配置文件如下:
# YOLOv5 🚀 by Ultralytics, AGPL-3.0 license# Parameters
nc: 80 # number of classes
depth_multiple: 0.33 # model depth multiple
width_multiple: 0.50 # layer channel multiple
anchors:- [10,13, 16,30, 33,23] # P3/8- [30,61, 62,45, 59,119] # P4/16- [116,90, 156,198, 373,326] # P5/32# YOLOv5 v6.0 backbone
backbone:# [from, number, module, args][[-1, 1, Focus, [64, 6, 2, 2]], # 0-P1/2[-1, 1, Conv, [128, 3, 2]], # 1-P2/4[-1, 3, C3, [128]],[-1, 1, Conv, [256, 3, 2]], # 3-P3/8[-1, 6, C3, [256]],[-1, 1, CoordAtt, []],[-1, 1, Conv, [512, 3, 2]], # 6-P4/16[-1, 9, C3, [512]],[-1, 1, CoordAtt, []],[-1, 1, Conv, [1024, 3, 2]], # 9-P5/32[-1, 3, C3, [1024]],[-1, 1, CoordAtt, []],[-1, 1, SPPF, [1024, 5]], # 12]# YOLOv5 v6.0 head
head:[[-1, 1, Conv, [512, 1, 1]],[-1, 1, nn.Upsample, [None, 2, 'nearest']],[[-1, 8], 1, Concat, [1]], # cat backbone P4[-1, 3, C3, [512, False]], # 13[-1, 1, Conv, [256, 1, 1]],[-1, 1, nn.Upsample, [None, 2, 'nearest']],[[-1, 5], 1, Concat, [1]], # cat backbone P3[-1, 3, C3, [256, False]], # 17 (P3/8-small)[-1, 1, Conv, [256, 3, 2]],[[-1, 17], 1, Concat, [1]], # cat head P4[-1, 3, C3, [512, False]], # 20 (P4/16-medium)[-1, 1, Conv, [512, 3, 2]],[[-1, 13], 1, Concat, [1]], # cat head P5[-1, 3, C3, [1024, False]], # 23 (P5/32-large)[[20, 23, 26], 1, Detect, [nc, anchors]], # Detect(P3, P4, P5)]
送书活动
用ChatGPT轻松玩转机器学习与深度学习
突破传统学习束缚,借助ChatGPT的神奇力量,解锁AI无限可能!
关键点
(1)利用ChatGPT,轻松理解机器学习和深度学习的概念和技术。
(2)提供实用经验和技巧,更好地掌握机器学习和深度学习的基本原理和方法。
(3)系统全面、易于理解,不需要过多的数学背景,只需掌握基本的编程知识即可上手。
内容简介
随着机器学习和深度学习技术的不断发展和进步,它们的复杂性也在不断增强。对于初学者来说,学习这两个领域可能会遇到许多难题和挑战,如理论知识的缺乏、数据处理的困难、算法选择的不确定性等。此时,ChatGPT可以提供强有力的帮助。利用ChatGPT,读者可以更轻松地理解机器学习和深度学习的概念和技术,并解决学习过程中遇到的各种问题和疑惑。此外,ChatGPT还可以为读者提供更多的实用经验和技巧,帮助他们更好地掌握机器学习和深度学习的基本原理和方法。本书主要内容包括探索性数据分析、有监督学习(线性回归、SVM、决策树等)、无监督学习(降维、聚类等),以及深度学习的基础原理和应用等。
本书旨在为广大读者提供一个系统全面、易于理解的机器学习和深度学习入门教程。不需要过多的数学背景,只需掌握基本的编程知识即可轻松上手。
作者简介
段小手,曾供职于百度、敦煌网、慧聪网、方正集团等知名IT企业。有多年的科技项目管理及开发经验。负责的项目曾获得“国家发改委电子商务示范项目”“中关村现代服务业试点项目”“北京市信息化基础设施提升专项”“北京市外贸公共服务平台”等多项政策支持。著有《深入浅出Python机器学习》《深入浅出Python量化交易实战》等著作,在与云南省公安厅合作期间,使用机器学习算法有效将某类案件发案率大幅降低。

当当网链接:《用ChatGPT轻松玩转机器学习与深度学习 突破传统学习束缚,借助ChatGPT的神奇力量,解锁AI无限可能 段小手》(段小手)【简介_书评_在线阅读】 - 当当图书
京东的链接:京东安全
关注博主、点赞、收藏、
评论区评论 “ 人生苦短,我爱python”
即可参与送书活动!
相关文章:

YOLOv5改进算法之添加CA注意力机制模块
目录 1.CA注意力机制 2.YOLOv5添加注意力机制 送书活动 1.CA注意力机制 CA(Coordinate Attention)注意力机制是一种用于加强深度学习模型对输入数据的空间结构理解的注意力机制。CA 注意力机制的核心思想是引入坐标信息,以便模型可以更好地…...
Jmeter系列-阶梯加压线程组Stepping Thread Group详解(6)
前言 tepping Thread Group是第一个自定义线程组但,随着版本的迭代,已经有更好的线程组代替Stepping Thread Group了【Concurrency Thread Group】,所以说Stepping Thread Group已经是过去式了,但还是介绍一下 Stepping Thread …...

图像的几何变换(缩放、平移、旋转)
图像的几何变换 学习目标 掌握图像的缩放、平移、旋转等了解数字图像的仿射变换和透射变换 1 图像的缩放 缩放是对图像的大小进行调整,即 使图像放大或缩小 cv2.resize(src,dsize,fx0,fy0,interpolationcv2.INTER_LINEAR) 参数: src :输入图像dsize…...

计算机网络第四章——网络层(上)
提示:朝碧海而暮苍梧,睹青天而攀白日 文章目录 网络层是路由器的最高层次,通过网络层就可以将各个设备连接到一起,从而实现这两个主机的数据通信和资源共享,之前学的数据链路层和物理层也是将两端连接起来,但是却没有网…...

【MyBatis】一、MyBatis概述与基本使用
Mybatis概述 Mybatis是一个半自动化的框架,需要自己写sql语句,对比JDBC其有耦合性更低的SQL语句与Java代码,各司其职不相互冗杂,对比Hibernate与JPA其又有更灵活的SQL编写能力。 环境搭建 引入相关依赖并打jar包 <dependenc…...

Java事件机制简介 内含面试题
面试题分享 云数据解决事务回滚问题 点我直达 2023最新面试合集链接 2023大厂面试题PDF 面试题PDF版本 java、python面试题 项目实战:AI文本 OCR识别最佳实践 AI Gamma一键生成PPT工具直达链接 玩转cloud Studio 在线编码神器 玩转 GPU AI绘画、AI讲话、翻译,GPU点亮…...

springMVC基础技术使用
目录 1.常用注解 1.1RequestMapping 1.2.RequestParam 1.3.RequestBody 1.4.PathVariable 2.参数传递 2.1 slf4j-----日志 2.2基础类型 2.3复杂类型 2.4RequestParam 2.5PathVariable 2.6RequestBody 2.7请求方法(增删改查) 3.返回值 3.1void …...

UI设计师的发展前景是否超越了平面设计?
这是一个现代经济学的典型话题:应该跟随趋势追逐风口,还是坚守成熟的“夕阳产业” UI 设计行业发展短短不过 20 多年,但平面设计这个“夕阳产业”最早可以追溯到上世纪的二三十年代。显而易见的答案是,更新兴的 UI 设计师得到的好…...

MyBatis的基本操作
目录 一、MyBatis的增删改查1、添加2、删除3、修改4、查询一个实体类对象5、查询集合 二、MyBatis的各种查询功能1、查询一个实体类对象2、查询一个list集合3、查询单个数据4、查询一条数据为map集合5、查询多条数据为map集合 三、特殊SQL的执行1、模糊查询2、批量删除3、动态设…...

【Tomcat】在SpringBoot项目中,Tomcat是如何处理HTTP请求的
目录 首先了解一下标准的Tomcat处理HTTP请求的流程 SpringBoot项目中Tomcat处理流程 首先了解一下标准的Tomcat处理HTTP请求的流程 监听端口:Tomcat 在启动时监听指定的端口,等待客户端发送请求。 接收请求:当客户端发起一个 HTTP 请…...

python开发基础篇1——后端操作K8s API方式
文章目录 一、基本了解1.1 操作k8s API1.2 基本使用 二、数据表格展示K8s常见资源2.1 Namespace2.2 Node2.3 PV2.4 Deployment2.5 DaemonSet2.6 StatefulSet2.7 Pod2.8 Service2.9 Ingress2.10 PVC2.11 ConfigMap2.12 Secret2.13 优化 一、基本了解 操作K8s资源api方式…...

【实践篇】Redis最强Java客户端(一)之Redisson入门介绍
Redisson入门介绍 文章目录 Redisson入门介绍1.1 Redisson简介1.1.1 起源和历史1.1.2 优势和特点1.1.3 与其他Java Redis客户端的比较 1.2 使用和配置1.2.1 依赖和SDK1.2.2 配置文件解析1.2.3 连接池配置 1.3 优雅的让Hash的某个Field过期2. 参考资料3. 源码地址4. Redis从入门…...
掌握AI助手的魔法工具:解密`Prompt`(提示)在AIGC时代的应用(下篇)
前言:在前面的两篇文章中,我们深入探讨了AI助手中的魔法工具——Prompt(提示)的基本概念以及在AIGC(Artificial Intelligence-Generated Content,人工智能生成内容)时代的应用场景。在本篇中&am…...
Stable Diffussion使用教程:Lora)
十)Stable Diffussion使用教程:Lora
LoRA 的全称为 Low-Rank Adaptation(低秩适应),是一种在机器学习中使用的方法,用于解决一些特殊问题,尤其是在数据中存在不均匀性的情况下表现较好。 要理解 LoRA,我们首先需要理解两个概念:低秩和适应。 低秩(Low Rank):在数学中,秩(Rank)是一个描述矩阵信息量的…...
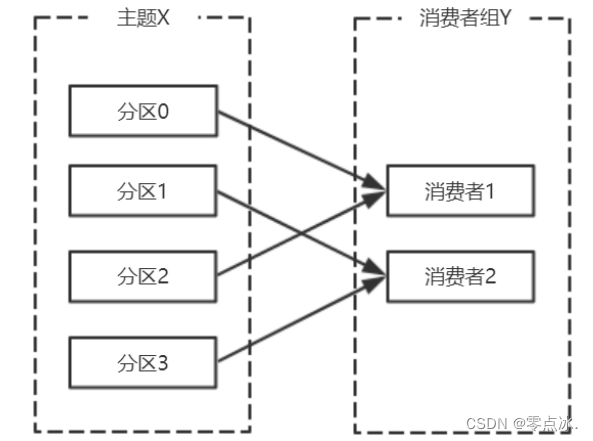
kafka学习-消费者
目录 1、消费者、消费组 2、心跳机制 3、消费者常见参数配置 4、订阅 5、反序列化 基本概念 自定义反序列化器 6、位移提交 6.1、自动提交 6.2、手动提交 同步提交 异步提交 7、再均衡 7.1、定义与基本概念 7.2、缺陷 7.3、如何避免再均衡 7.4、如何进行组内分…...
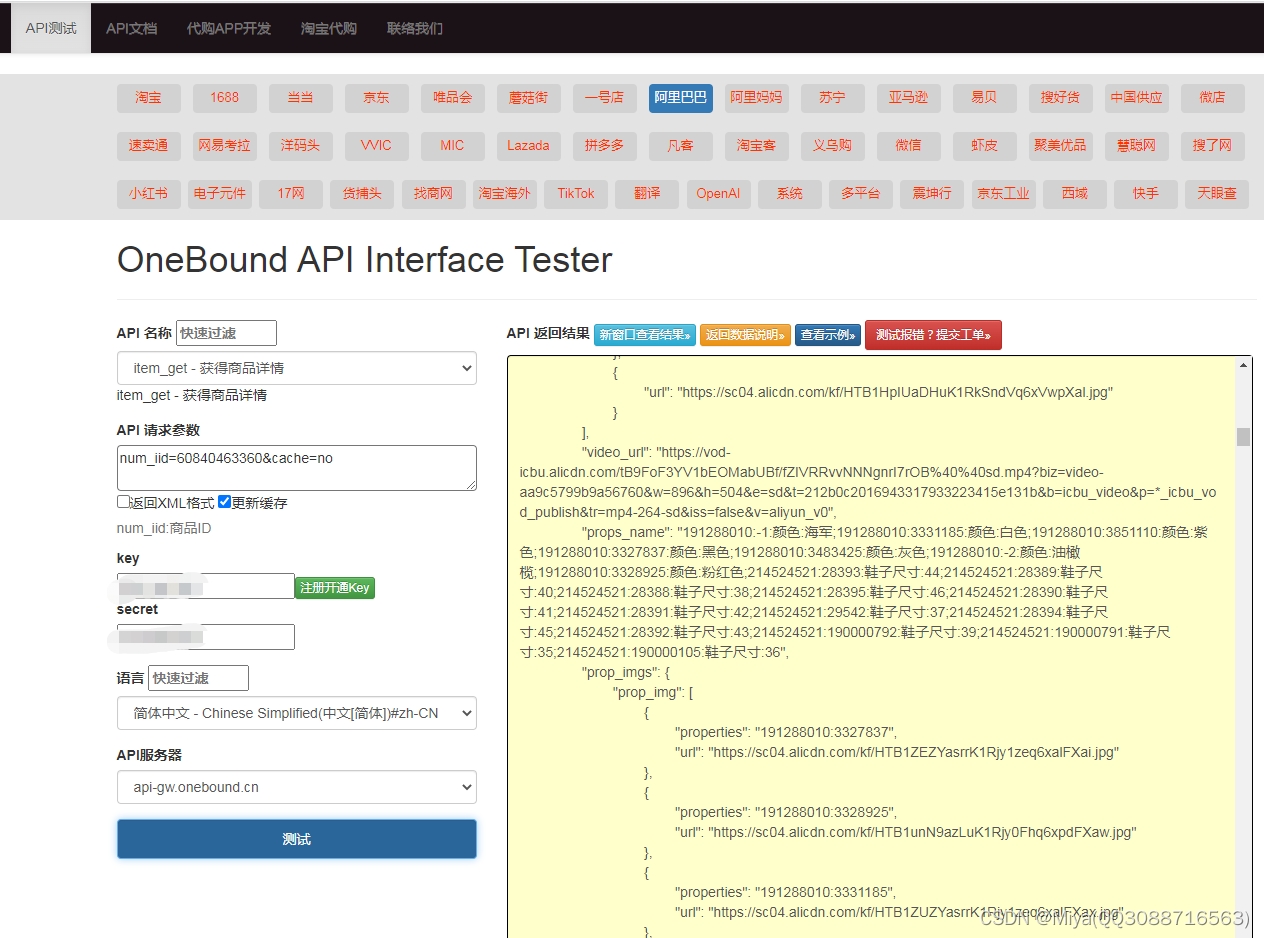
Alibaba(商品详情)API接口
为了进行电商平台 的API开发,首先我们需要做下面几件事情。 1)开发者注册一个账号 2)然后为每个alibaba应用注册一个应用程序键(App Key) 。 3)下载alibaba API的SDK并掌握基本的API基础知识和调用 4)利…...

OLED透明屏触控:引领未来科技革命的创新力量
OLED透明屏触控技术作为一项颠覆性的创新,正在引领新一轮科技革命。它将OLED显示技术与触摸技术相结合,实现了透明度和触控功能的完美融合。 在这篇文章中,尼伽将通过引用最新的市场数据、报告和行业动态,详细介绍OLED透明屏触控…...
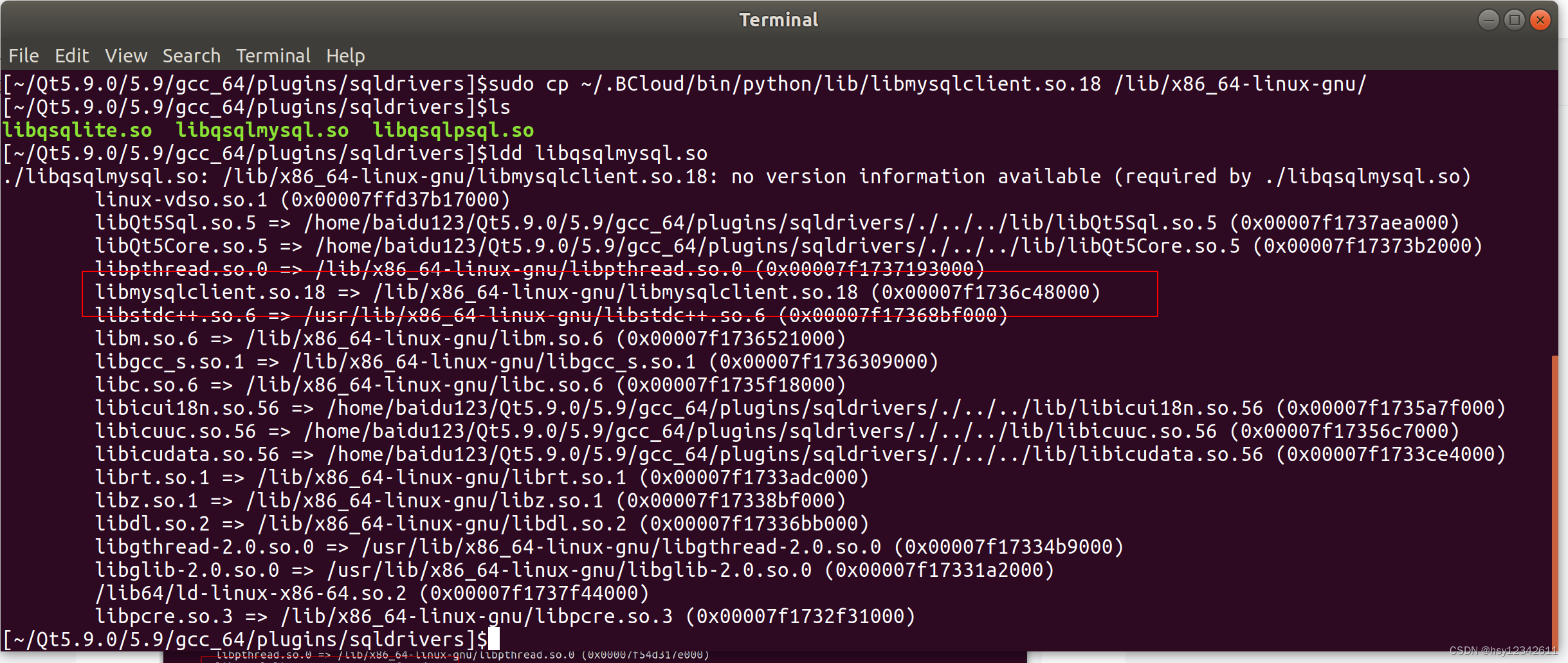
Ubuntu下QT操作Mysql数据库
本篇总结一下一下Ubuntu下QT操作Mysql数据库。 目录 1. 启动Mysql数据库服务器 2.查看QT支持的数据库驱动 3.连接数据库 4. 增加表和记录 5. 删除记录 6. 修改记录 7. 查询记录 8.完整代码和运行效果 常见错误总结: (1) 数据库服务没启动报错信息 (2) 有…...
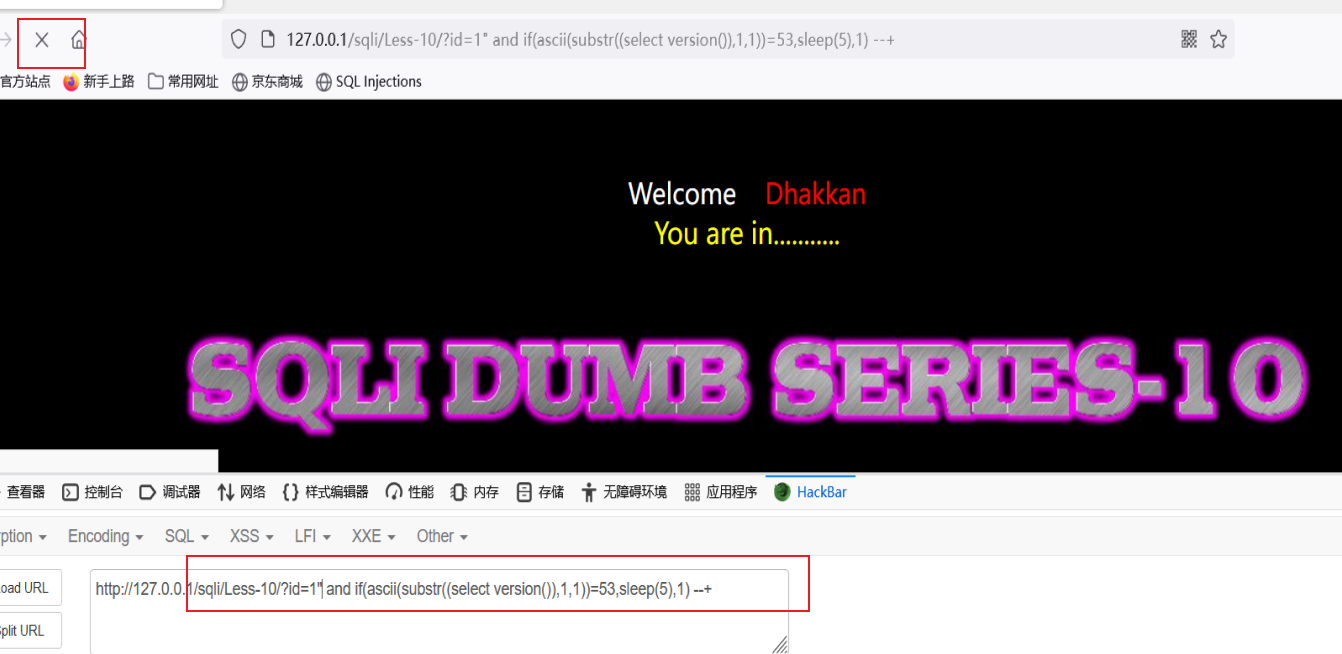
sqli --【1--10】
Less-1(联合查询) 1.查看是否有回显 2.查看是否有报错 3.使用联合查询(字符注入) 3.1判断其列数 3.2 判断显示位置 3.3敏感信息查询 Less-2(联合查询) 1.查看是否有回显 2.查看是否有报错 3.使用…...

《自然语言处理(NLP)的最新进展:Transformers与GPT-4的浅析》
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...
